4.3.2二倍角公式的综合应用同步练习2020-2021学年高一下学期数学北师版(2019)必修第二册第四章(Word含答案解析)
文档属性
| 名称 | 4.3.2二倍角公式的综合应用同步练习2020-2021学年高一下学期数学北师版(2019)必修第二册第四章(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览



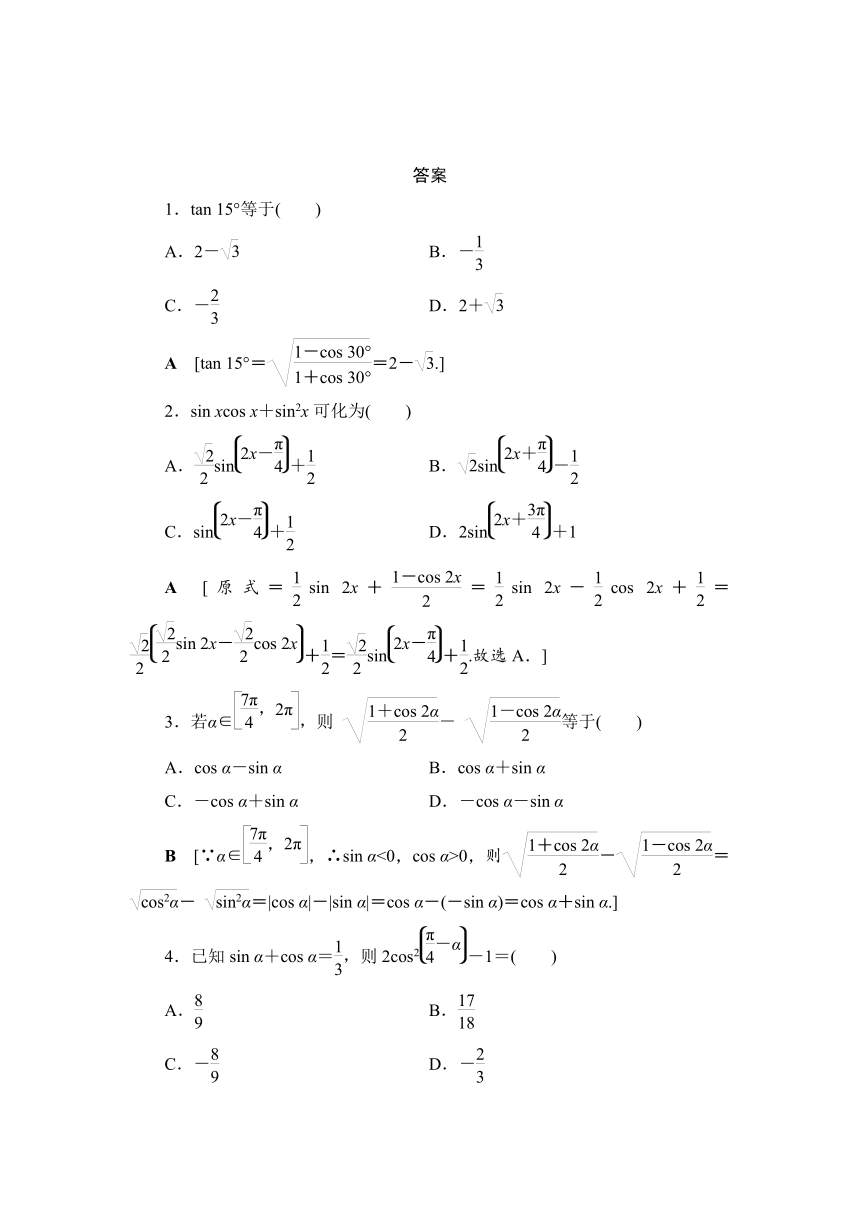
文档简介
二倍角公式的综合应用
1.tan
15°等于( )
A.2-
B.-
C.-
D.2+
2.sin
xcos
x+sin2x可化为( )
A.sin+
B.sin-
C.sin+
D.2sin+1
3.若α∈,则
-
等于( )
A.cos
α-sin
α
B.cos
α+sin
α
C.-cos
α+sin
α
D.-cos
α-sin
α
4.已知sin
α+cos
α=,则2cos2-1=( )
A.
B.
C.-
D.-
5.函数y=sin+cos的最小正周期和最大值分别为( )
A.π,1
B.π,
C.2π,1
D.2π,
6.设5π<θ<6π,cos=a,则sin
的值为________.
7.若3sin
x-cos
x=2sin(x+φ),φ∈(-π,π),则φ=________.
8.函数y=sin
2x+cos2x的最小正周期为________.
9.化简:(0<α<π).
10.已知函数f(x)=2sin
x·cos
x+1-2sin2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间上的最大值与最小值.
11.(多选)如果若干个函数的图像经过平移后能够重合,则称这些函数为“同族函数”.给出下列函数,其中与函数f(x)=sin
x-cos
x是“同族函数”的是( )
A.f(x)=2sin
x·cos
x+1
B.f(x)=2sin
C.f(x)=sin
x+cos
x
D.f(x)=sin
2x+1
12.
设函数f(x)=sin-cos的图象关于y轴对称,则θ=( )
A.-
B.
C.-
D.
13.
函数f(x)=sin2x+cos
x-的最大值是________.
14.已知A+B=,那么cos2A+cos2B的最大值是________,最小值是________.
15.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100
米,宽BC=50
米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE,HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
(1)设∠CHE=x(弧度),试将三条路的全长(即△HEF的周长)L表示成x的函数,并求出此函数的定义域;
(2)这三条路,每米铺设预算费用均为400
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用(结果保留整数)(可能用到的参考值:取1.732,取1.414).
答案
1.tan
15°等于( )
A.2-
B.-
C.-
D.2+
A [tan
15°==2-.]
2.sin
xcos
x+sin2x可化为( )
A.sin+
B.sin-
C.sin+
D.2sin+1
A [原式=sin
2x+=sin
2x-cos
2x+=+=sin+.故选A.]
3.若α∈,则
-
等于( )
A.cos
α-sin
α
B.cos
α+sin
α
C.-cos
α+sin
α
D.-cos
α-sin
α
B [∵α∈,∴sin
α<0,cos
α>0,则-=-
=|cos
α|-|sin
α|=cos
α-(-sin
α)=cos
α+sin
α.]
4.已知sin
α+cos
α=,则2cos2-1=( )
A.
B.
C.-
D.-
C [∵sin
α+cos
α=,平方可得1+sin
2α=,可得sin
2α=-.
2cos2-1=cos=sin
2α=-.]
5.函数y=sin+cos的最小正周期和最大值分别为( )
A.π,1
B.π,
C.2π,1
D.2π,
A [∵y=sin+cos=+
=cos
2x,
∴该函数的最小正周期为π,最大值为1.]
6.设5π<θ<6π,cos=a,则sin
的值为________.
- [sin2=,∵θ∈(5π,6π),
∴∈.
∴sin
=-=-.]
7.若3sin
x-cos
x=2sin(x+φ),φ∈(-π,π),则φ=________.
- [∵3sin
x-cos
x=2=2sin,因φ∈(-π,π),∴φ=-.]
8.函数y=sin
2x+cos2x的最小正周期为________.
π [y=sin
2x+cos2x=sin
2x+=sin
2x+cos
2x+=sin+,所以该函数的最小正周期为π.]
9.化简:(0<α<π).
[解] ∵tan=,∴(1+cos
α)tan=sin
α.
又∵cos=-sin
α,且1-cos
α=2sin2,
∴原式===-.
∵0<α<π,∴0<<,∴sin>0.
∴原式=-2cos.
10.已知函数f(x)=2sin
x·cos
x+1-2sin2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间上的最大值与最小值.
[解] (1)因为f(x)=sin
2x+cos
2x=sin,
所以f(x)的最小正周期为π.
(2)因为-≤x≤,所以-≤2x+≤.
当2x+=,即x=时,f(x)取得最大值;
当2x+=-,即x=-时,
f(x)min=f
=sin+cos=-,
即f(x)的最小值为-.
11.(多选)如果若干个函数的图像经过平移后能够重合,则称这些函数为“同族函数”.给出下列函数,其中与函数f(x)=sin
x-cos
x是“同族函数”的是( )
A.f(x)=2sin
x·cos
x+1
B.f(x)=2sin
C.f(x)=sin
x+cos
x
D.f(x)=sin
2x+1
BC [A式化简f(x)=sin
2x+1,
C式化简f(x)=2sin,
f(x)=sin
x-cos
x=2sin,
显然A中的周期、D中的振幅和周期与已知函数不符,B、C符合.]
12.
设函数f(x)=sin-cos的图象关于y轴对称,则θ=( )
A.-
B.
C.-
D.
A [f(x)=sin-cos=2sin,
由题意可得f(0)=2sin=±2,即sin=±1,∴θ-=+kπ(k∈Z),
∴θ=+kπ(k∈Z).
∵|θ|<,∴k=-1时,θ=-.]
13.
函数f(x)=sin2x+cos
x-的最大值是________.
1 [由题意可得f(x)=-cos2x+cos
x+
=-(cos
x-)2+1.
∵x∈,∴cos
x∈[0,1].
∴当cos
x=,即x=时,f(x)max=1.]
14.已知A+B=,那么cos2A+cos2B的最大值是________,最小值是________.
[∵A+B=,∴cos2A+cos2B=(1+cos
2A+1+cos
2B)=1+(cos
2A+cos
2B)
=1+cos(A+B)cos(A-B)=1+coscos(A-B)=1-cos(A-B),
∴当cos(A-B)=-1时,原式取得最大值;
当cos(A-B)=1时,原式取得最小值.]
15.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100
米,宽BC=50
米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE,HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
(1)设∠CHE=x(弧度),试将三条路的全长(即△HEF的周长)L表示成x的函数,并求出此函数的定义域;
(2)这三条路,每米铺设预算费用均为400
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用(结果保留整数)(可能用到的参考值:取1.732,取1.414).
[解]
(1)∵在Rt△CHE中,CH=50,∠C=90°,
∠CHE=x,∴HE=.
在Rt△HDF中,HD=50,∠D=90°,∠DFH=x,
∴HF=.
又∠EHF=90°,∴EF=,
∴三条路的全长(即△HEF的周长)L=.
当点F在A点时,这时角x最小,求得此时x=;
当点E在B点时,这时角x最大,求得此时x=.
故此函数的定义域为.
(2)由题意知,要求铺路总费用最低,只要求△HEF的周长L的最小值即可.
由(1)得L=,x∈,
设sin
x+cos
x=t,则sin
xcos
x=,∴L==.
由t=sin
x+cos
x=sin,x∈,得≤t≤,
从而+1≤≤+1,
当x=,即CE=50时,Lmin=100(+1),
当CE=DF=50
米时,铺路总费用最低,最低总费用为96
560
元.
1.tan
15°等于( )
A.2-
B.-
C.-
D.2+
2.sin
xcos
x+sin2x可化为( )
A.sin+
B.sin-
C.sin+
D.2sin+1
3.若α∈,则
-
等于( )
A.cos
α-sin
α
B.cos
α+sin
α
C.-cos
α+sin
α
D.-cos
α-sin
α
4.已知sin
α+cos
α=,则2cos2-1=( )
A.
B.
C.-
D.-
5.函数y=sin+cos的最小正周期和最大值分别为( )
A.π,1
B.π,
C.2π,1
D.2π,
6.设5π<θ<6π,cos=a,则sin
的值为________.
7.若3sin
x-cos
x=2sin(x+φ),φ∈(-π,π),则φ=________.
8.函数y=sin
2x+cos2x的最小正周期为________.
9.化简:(0<α<π).
10.已知函数f(x)=2sin
x·cos
x+1-2sin2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间上的最大值与最小值.
11.(多选)如果若干个函数的图像经过平移后能够重合,则称这些函数为“同族函数”.给出下列函数,其中与函数f(x)=sin
x-cos
x是“同族函数”的是( )
A.f(x)=2sin
x·cos
x+1
B.f(x)=2sin
C.f(x)=sin
x+cos
x
D.f(x)=sin
2x+1
12.
设函数f(x)=sin-cos的图象关于y轴对称,则θ=( )
A.-
B.
C.-
D.
13.
函数f(x)=sin2x+cos
x-的最大值是________.
14.已知A+B=,那么cos2A+cos2B的最大值是________,最小值是________.
15.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100
米,宽BC=50
米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE,HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
(1)设∠CHE=x(弧度),试将三条路的全长(即△HEF的周长)L表示成x的函数,并求出此函数的定义域;
(2)这三条路,每米铺设预算费用均为400
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用(结果保留整数)(可能用到的参考值:取1.732,取1.414).
答案
1.tan
15°等于( )
A.2-
B.-
C.-
D.2+
A [tan
15°==2-.]
2.sin
xcos
x+sin2x可化为( )
A.sin+
B.sin-
C.sin+
D.2sin+1
A [原式=sin
2x+=sin
2x-cos
2x+=+=sin+.故选A.]
3.若α∈,则
-
等于( )
A.cos
α-sin
α
B.cos
α+sin
α
C.-cos
α+sin
α
D.-cos
α-sin
α
B [∵α∈,∴sin
α<0,cos
α>0,则-=-
=|cos
α|-|sin
α|=cos
α-(-sin
α)=cos
α+sin
α.]
4.已知sin
α+cos
α=,则2cos2-1=( )
A.
B.
C.-
D.-
C [∵sin
α+cos
α=,平方可得1+sin
2α=,可得sin
2α=-.
2cos2-1=cos=sin
2α=-.]
5.函数y=sin+cos的最小正周期和最大值分别为( )
A.π,1
B.π,
C.2π,1
D.2π,
A [∵y=sin+cos=+
=cos
2x,
∴该函数的最小正周期为π,最大值为1.]
6.设5π<θ<6π,cos=a,则sin
的值为________.
- [sin2=,∵θ∈(5π,6π),
∴∈.
∴sin
=-=-.]
7.若3sin
x-cos
x=2sin(x+φ),φ∈(-π,π),则φ=________.
- [∵3sin
x-cos
x=2=2sin,因φ∈(-π,π),∴φ=-.]
8.函数y=sin
2x+cos2x的最小正周期为________.
π [y=sin
2x+cos2x=sin
2x+=sin
2x+cos
2x+=sin+,所以该函数的最小正周期为π.]
9.化简:(0<α<π).
[解] ∵tan=,∴(1+cos
α)tan=sin
α.
又∵cos=-sin
α,且1-cos
α=2sin2,
∴原式===-.
∵0<α<π,∴0<<,∴sin>0.
∴原式=-2cos.
10.已知函数f(x)=2sin
x·cos
x+1-2sin2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间上的最大值与最小值.
[解] (1)因为f(x)=sin
2x+cos
2x=sin,
所以f(x)的最小正周期为π.
(2)因为-≤x≤,所以-≤2x+≤.
当2x+=,即x=时,f(x)取得最大值;
当2x+=-,即x=-时,
f(x)min=f
=sin+cos=-,
即f(x)的最小值为-.
11.(多选)如果若干个函数的图像经过平移后能够重合,则称这些函数为“同族函数”.给出下列函数,其中与函数f(x)=sin
x-cos
x是“同族函数”的是( )
A.f(x)=2sin
x·cos
x+1
B.f(x)=2sin
C.f(x)=sin
x+cos
x
D.f(x)=sin
2x+1
BC [A式化简f(x)=sin
2x+1,
C式化简f(x)=2sin,
f(x)=sin
x-cos
x=2sin,
显然A中的周期、D中的振幅和周期与已知函数不符,B、C符合.]
12.
设函数f(x)=sin-cos的图象关于y轴对称,则θ=( )
A.-
B.
C.-
D.
A [f(x)=sin-cos=2sin,
由题意可得f(0)=2sin=±2,即sin=±1,∴θ-=+kπ(k∈Z),
∴θ=+kπ(k∈Z).
∵|θ|<,∴k=-1时,θ=-.]
13.
函数f(x)=sin2x+cos
x-的最大值是________.
1 [由题意可得f(x)=-cos2x+cos
x+
=-(cos
x-)2+1.
∵x∈,∴cos
x∈[0,1].
∴当cos
x=,即x=时,f(x)max=1.]
14.已知A+B=,那么cos2A+cos2B的最大值是________,最小值是________.
[∵A+B=,∴cos2A+cos2B=(1+cos
2A+1+cos
2B)=1+(cos
2A+cos
2B)
=1+cos(A+B)cos(A-B)=1+coscos(A-B)=1-cos(A-B),
∴当cos(A-B)=-1时,原式取得最大值;
当cos(A-B)=1时,原式取得最小值.]
15.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100
米,宽BC=50
米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE,HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
(1)设∠CHE=x(弧度),试将三条路的全长(即△HEF的周长)L表示成x的函数,并求出此函数的定义域;
(2)这三条路,每米铺设预算费用均为400
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用(结果保留整数)(可能用到的参考值:取1.732,取1.414).
[解]
(1)∵在Rt△CHE中,CH=50,∠C=90°,
∠CHE=x,∴HE=.
在Rt△HDF中,HD=50,∠D=90°,∠DFH=x,
∴HF=.
又∠EHF=90°,∴EF=,
∴三条路的全长(即△HEF的周长)L=.
当点F在A点时,这时角x最小,求得此时x=;
当点E在B点时,这时角x最大,求得此时x=.
故此函数的定义域为.
(2)由题意知,要求铺路总费用最低,只要求△HEF的周长L的最小值即可.
由(1)得L=,x∈,
设sin
x+cos
x=t,则sin
xcos
x=,∴L==.
由t=sin
x+cos
x=sin,x∈,得≤t≤,
从而+1≤≤+1,
当x=,即CE=50时,Lmin=100(+1),
当CE=DF=50
米时,铺路总费用最低,最低总费用为96
560
元.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
