6.6.3球的表面积和体积2020-2021年高一下学期数学北师大版(2019)必修第二册第六章课时作业(Word含答案解析)
文档属性
| 名称 | 6.6.3球的表面积和体积2020-2021年高一下学期数学北师大版(2019)必修第二册第六章课时作业(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 340.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 21:37:46 | ||
图片预览



文档简介
球的表面积和体积
1.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为( )
A.
B.
C.8π
D.
2.设正方体的表面积为24
cm2,一个球内切于该正方体,那么这个球的体积是( )
A.π
cm3
B.π
cm3
C.π
cm3
D.π
cm3
3.若一个圆锥的底面半径和一个半球的半径相等,体积也相等,则圆锥的高与球的半径之比为( )
A.2∶1
B.2∶3
C.2∶π
D.2∶5
4.等体积的球和正方体的表面积S球与S正方体的大小关系是( )
A.S正方体>S球
B.S正方体C.S正方体=S球
D.无法确定
5.圆柱形容器内盛有高度为6
cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,如图所示.则球的半径是( )
A.1
cm
B.2
cm
C.3
cm
D.4
cm
6.两个球的半径相差1,表面积之差为28π,则它们的体积和为________.
7.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
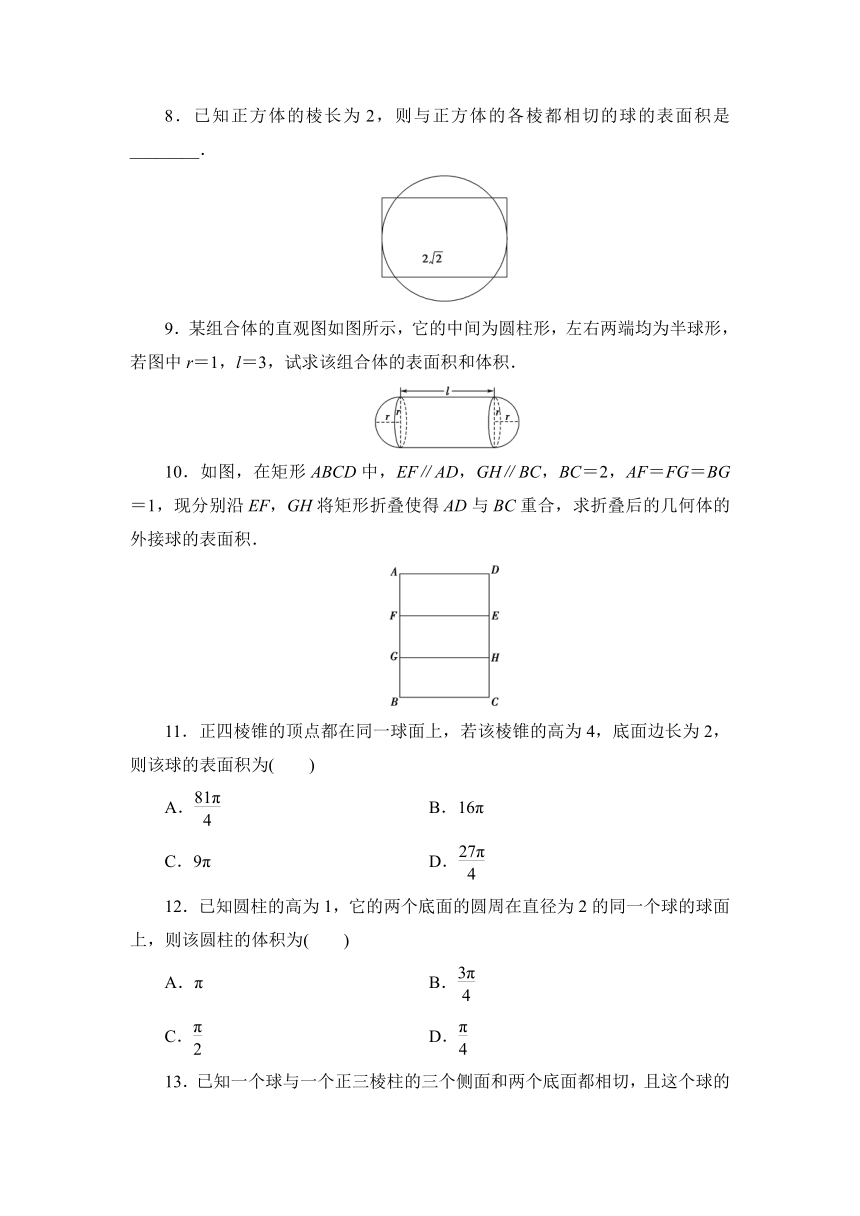
8.已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是________.
9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
10.如图,在矩形ABCD中,EF∥AD,GH∥BC,BC=2,AF=FG=BG=1,现分别沿EF,GH将矩形折叠使得AD与BC重合,求折叠后的几何体的外接球的表面积.
11.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A.
B.16π
C.9π
D.
12.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π
B.
C.
D.
13.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是π,那么这个三棱柱的体积是________.
14.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为________.
15.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
答案
1.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为( )
A.
B.
C.8π
D.
C [设球的半径为R,则截面圆的半径为,
∴截面圆的面积为S=π2=(R2-1)π=π,∴R2=2,∴球的表面积S=4πR2=8π.]
2.设正方体的表面积为24
cm2,一个球内切于该正方体,那么这个球的体积是( )
A.π
cm3
B.π
cm3
C.π
cm3
D.π
cm3
D [由正方体的表面积为24
cm2,得正方体的棱长为2
cm,故这个球的直径为2
cm,故这个球的体积为π
cm3.]
3.若一个圆锥的底面半径和一个半球的半径相等,体积也相等,则圆锥的高与球的半径之比为( )
A.2∶1
B.2∶3
C.2∶π
D.2∶5
A [设半球的半径为r,圆锥的高为h,则πr2h=πr3×,所以h=2r,故选A.]
4.等体积的球和正方体的表面积S球与S正方体的大小关系是( )
A.S正方体>S球
B.S正方体C.S正方体=S球
D.无法确定
A [设正方体的棱长为a,球的半径为R,由题意,得V=πR3=a3,∴a=,R=,∴S正方体=6a2=6=,S球=4πR2=<.]
5.圆柱形容器内盛有高度为6
cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,如图所示.则球的半径是( )
A.1
cm
B.2
cm
C.3
cm
D.4
cm
C [设球半径为r,则由3V球+V水=V柱,可得3×πr3+πr2×6=πr2×6r,解得r=3.]
6.两个球的半径相差1,表面积之差为28π,则它们的体积和为________.
[设大,小两球半径分别为R,r,则所以
所以体积和为πR3+πr3=.]
7.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
[设球的半径为R,正方体棱长为a,则V球=πR3=π,得到R=,正方体体对角线的长为a=2R,则a=,所以正方体的棱长为.]
8.已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是________.
8π [过正方体的对角面作截面如图.故球的半径r=,
∴其表面积S=4π×()2=8π.]
9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
[解] 该组合体的表面积S=4πr2+2πrl=4π×12+2π×1×3=10π,
该组合体的体积V=πr3+πr2l=π×13+π×12×3=.
10.如图,在矩形ABCD中,EF∥AD,GH∥BC,BC=2,AF=FG=BG=1,现分别沿EF,GH将矩形折叠使得AD与BC重合,求折叠后的几何体的外接球的表面积.
[解] 由题意得,折叠后的几何体为正三棱柱,且该三棱柱的底面边长为1,高为2.如图所示的正三棱柱ABC-A1B1C1.
设上下底面的中心分别为O1,O2,则球心O为O1,O2的中点,连OC,O2C,
则O2C=×(×1)=,OO2=1,
∴OC==eq
\r(\b\lc\(\rc\)(\a\vs4\al\co1(\f(\r(3),3)))+1)=,即球半径R=,
∴该几何体的外接球的表面积为S=4πR2=4π×=.
11.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A.
B.16π
C.9π
D.
A [如图所示,设球半径为R,底面中心为O′且球心为O,
∵正四棱锥P-ABCD中AB=2,∴AO′=.
∵PO′=4,∴在Rt△AOO′中,AO2=AO′2+OO′2,
∴R2=()2+(4-R)2,解得R=,
∴该球的表面积为S=4πR2=4π×=,故选A.]
12.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π
B.
C.
D.
B [如图画出圆柱的轴截面ABCD,O为球心.球半径R=OA=1,球心到底面圆的距离为OM=.
∴底面圆半径r==,故圆柱体积V=πr2h=π×1=.]
13.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是π,那么这个三棱柱的体积是________.
48 [设球的半径为r,则πr3=π,得r=2,柱体的高为2r=4.又正三棱柱的底面三角形的内切圆半径与球的半径相等,所以底面正三角形的边长为4,所以正三棱柱的体积V=×(4)2×4=48.]
14.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为________.
[连接BC1,与B1C交于点O,则O为平面BCC1B1的中心.由题意知,球心为侧面BCC1B1的中心O,BC1为截面圆的直径,所以∠BAC=90°,则△ABC的外接圆圆心N位于BC的中点,同理,△A1B1C1的外接圆圆心M位于B1C1的中点,设正方形BCC1B1的边长为x,在Rt△OMC1中,OM=,MC1=,OC1=R=1(R为球的半径),所以+=1,即x=,即AB=AC=1,所以侧面ABB1A1的面积为×1=.]
15.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
[解] 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.
根据切线性质知,当球在容器内时,水深为3r,水面的半径为r,
则容器内水的体积为V=V圆锥-V球=π·(r)2·3r-πr3=πr3,
而将球取出后,设容器内水的深度为h,则水面圆的半径为h,
从而容器内水的体积是V′=π··h=πh3,由V=V′,得h=r.
即容器中水的深度为r.
1.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为( )
A.
B.
C.8π
D.
2.设正方体的表面积为24
cm2,一个球内切于该正方体,那么这个球的体积是( )
A.π
cm3
B.π
cm3
C.π
cm3
D.π
cm3
3.若一个圆锥的底面半径和一个半球的半径相等,体积也相等,则圆锥的高与球的半径之比为( )
A.2∶1
B.2∶3
C.2∶π
D.2∶5
4.等体积的球和正方体的表面积S球与S正方体的大小关系是( )
A.S正方体>S球
B.S正方体
D.无法确定
5.圆柱形容器内盛有高度为6
cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,如图所示.则球的半径是( )
A.1
cm
B.2
cm
C.3
cm
D.4
cm
6.两个球的半径相差1,表面积之差为28π,则它们的体积和为________.
7.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
8.已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是________.
9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
10.如图,在矩形ABCD中,EF∥AD,GH∥BC,BC=2,AF=FG=BG=1,现分别沿EF,GH将矩形折叠使得AD与BC重合,求折叠后的几何体的外接球的表面积.
11.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A.
B.16π
C.9π
D.
12.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π
B.
C.
D.
13.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是π,那么这个三棱柱的体积是________.
14.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为________.
15.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
答案
1.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为( )
A.
B.
C.8π
D.
C [设球的半径为R,则截面圆的半径为,
∴截面圆的面积为S=π2=(R2-1)π=π,∴R2=2,∴球的表面积S=4πR2=8π.]
2.设正方体的表面积为24
cm2,一个球内切于该正方体,那么这个球的体积是( )
A.π
cm3
B.π
cm3
C.π
cm3
D.π
cm3
D [由正方体的表面积为24
cm2,得正方体的棱长为2
cm,故这个球的直径为2
cm,故这个球的体积为π
cm3.]
3.若一个圆锥的底面半径和一个半球的半径相等,体积也相等,则圆锥的高与球的半径之比为( )
A.2∶1
B.2∶3
C.2∶π
D.2∶5
A [设半球的半径为r,圆锥的高为h,则πr2h=πr3×,所以h=2r,故选A.]
4.等体积的球和正方体的表面积S球与S正方体的大小关系是( )
A.S正方体>S球
B.S正方体
D.无法确定
A [设正方体的棱长为a,球的半径为R,由题意,得V=πR3=a3,∴a=,R=,∴S正方体=6a2=6=,S球=4πR2=<.]
5.圆柱形容器内盛有高度为6
cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,如图所示.则球的半径是( )
A.1
cm
B.2
cm
C.3
cm
D.4
cm
C [设球半径为r,则由3V球+V水=V柱,可得3×πr3+πr2×6=πr2×6r,解得r=3.]
6.两个球的半径相差1,表面积之差为28π,则它们的体积和为________.
[设大,小两球半径分别为R,r,则所以
所以体积和为πR3+πr3=.]
7.已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________.
[设球的半径为R,正方体棱长为a,则V球=πR3=π,得到R=,正方体体对角线的长为a=2R,则a=,所以正方体的棱长为.]
8.已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是________.
8π [过正方体的对角面作截面如图.故球的半径r=,
∴其表面积S=4π×()2=8π.]
9.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
[解] 该组合体的表面积S=4πr2+2πrl=4π×12+2π×1×3=10π,
该组合体的体积V=πr3+πr2l=π×13+π×12×3=.
10.如图,在矩形ABCD中,EF∥AD,GH∥BC,BC=2,AF=FG=BG=1,现分别沿EF,GH将矩形折叠使得AD与BC重合,求折叠后的几何体的外接球的表面积.
[解] 由题意得,折叠后的几何体为正三棱柱,且该三棱柱的底面边长为1,高为2.如图所示的正三棱柱ABC-A1B1C1.
设上下底面的中心分别为O1,O2,则球心O为O1,O2的中点,连OC,O2C,
则O2C=×(×1)=,OO2=1,
∴OC==eq
\r(\b\lc\(\rc\)(\a\vs4\al\co1(\f(\r(3),3)))+1)=,即球半径R=,
∴该几何体的外接球的表面积为S=4πR2=4π×=.
11.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A.
B.16π
C.9π
D.
A [如图所示,设球半径为R,底面中心为O′且球心为O,
∵正四棱锥P-ABCD中AB=2,∴AO′=.
∵PO′=4,∴在Rt△AOO′中,AO2=AO′2+OO′2,
∴R2=()2+(4-R)2,解得R=,
∴该球的表面积为S=4πR2=4π×=,故选A.]
12.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π
B.
C.
D.
B [如图画出圆柱的轴截面ABCD,O为球心.球半径R=OA=1,球心到底面圆的距离为OM=.
∴底面圆半径r==,故圆柱体积V=πr2h=π×1=.]
13.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是π,那么这个三棱柱的体积是________.
48 [设球的半径为r,则πr3=π,得r=2,柱体的高为2r=4.又正三棱柱的底面三角形的内切圆半径与球的半径相等,所以底面正三角形的边长为4,所以正三棱柱的体积V=×(4)2×4=48.]
14.如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为1的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为________.
[连接BC1,与B1C交于点O,则O为平面BCC1B1的中心.由题意知,球心为侧面BCC1B1的中心O,BC1为截面圆的直径,所以∠BAC=90°,则△ABC的外接圆圆心N位于BC的中点,同理,△A1B1C1的外接圆圆心M位于B1C1的中点,设正方形BCC1B1的边长为x,在Rt△OMC1中,OM=,MC1=,OC1=R=1(R为球的半径),所以+=1,即x=,即AB=AC=1,所以侧面ABB1A1的面积为×1=.]
15.有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
[解] 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.
根据切线性质知,当球在容器内时,水深为3r,水面的半径为r,
则容器内水的体积为V=V圆锥-V球=π·(r)2·3r-πr3=πr3,
而将球取出后,设容器内水的深度为h,则水面圆的半径为h,
从而容器内水的体积是V′=π··h=πh3,由V=V′,得h=r.
即容器中水的深度为r.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
