《长方体和正方体体积的统一公式》(课件) 数学六年级上册 苏教版 ( 18张ppt)
文档属性
| 名称 | 《长方体和正方体体积的统一公式》(课件) 数学六年级上册 苏教版 ( 18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 06:33:33 | ||
图片预览




文档简介
(共18张PPT)
长方体和正方体体积的统一公式
苏教版六年级上
教学目标
让学生在具体情境中经历比较、分析、验证、归纳的过程,掌握长方体(正方体)的体积等于底面积乘高的计算方法。
使学生在活动中进一步积累空间与图形的学习经验,增强空间观念,发展数学思维。
使学生进一步体会图形与实际生活的联系,感受图形学习的价值,提高对数学的兴趣和对生活的热爱。
复习导入
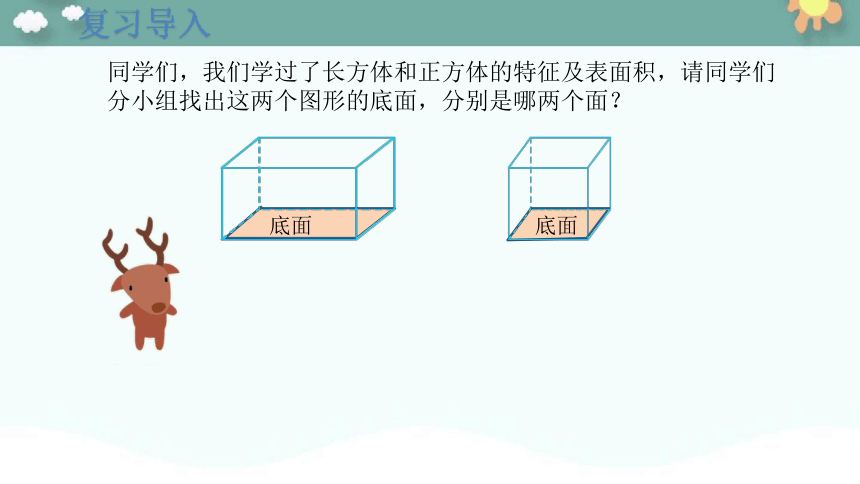
同学们,我们学过了长方体和正方体的特征及表面积,请同学们分小组找出这两个图形的底面,分别是哪两个面?
底面
底面
复习导入
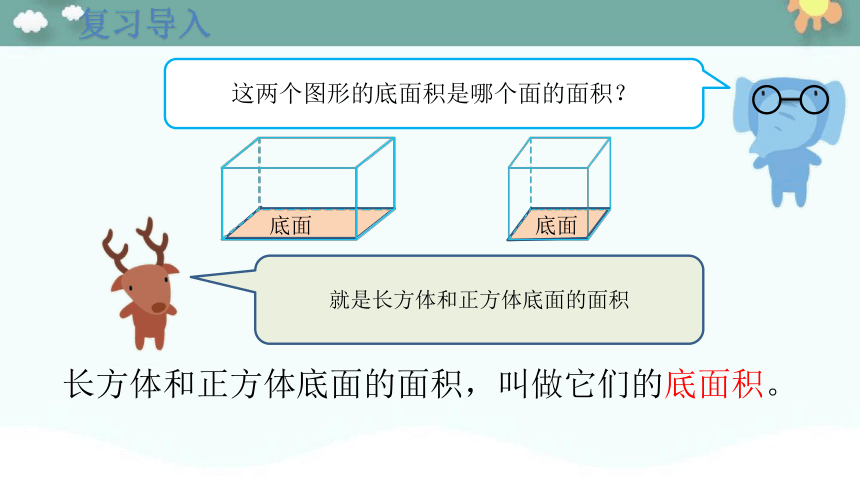
这两个图形的底面积是哪个面的面积?
就是长方体和正方体底面的面积
底面
底面
长方体和正方体底面的面积,叫做它们的底面积。
怎样计算长方体和正方体的底面积?
长方体的底面积=长×宽
正方体的底面积=棱长×棱长
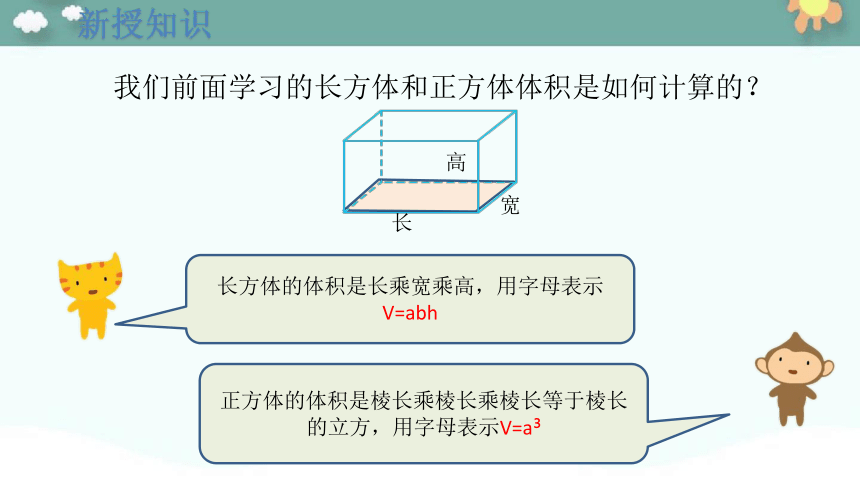
我们前面学习的长方体和正方体体积是如何计算的?
新授知识
长方体的体积是长乘宽乘高,用字母表示V=abh
正方体的体积是棱长乘棱长乘棱长等于棱长的立方,用字母表示V=a?
长
宽
高
长方体和正方体的体积也可以,这样来计算
长方体的体积=底面积×高
底面
接下来请同学们,在小组中讨论讨论为什么可以这样来计算长方体和正方体的体积?
讨论与交流
长方体的体积=底面积×高
我是这样想的,长方体的长乘宽就是长方体的底面积,所以长方体的体积计算公式可以写成“长方体的体积=底面积×高”
讨论与交流
长方体的体积=底面积×高
如果用s表示底面积,那么长方体和正方体的体积还可以怎样表示,请同学尝试用字母表示这个公式。
因为长方体的长乘宽就是长方体的底面积,所以字母公式中把ab改成S就行了,也就是V=Sh
把aa换成S,另外一个棱也可以看成是高,也可以用V=Sh表示
分析与比较
1、先计算长方体和正方体的底面积,再计算它们的体积。
10m
8m
26m
4cm
4cm
4cm
底面积=4×4=16(cm?)
底面积=10×8=80(m?)
体积=16×4=64(cm?)
体积=80×26=2080(m?)
2、一个长方体底面积是16平方厘米,高是5厘米,求它的体积。
16×5=80(cm?)
底面积16cm?
3、一块长方体石料,长3米横截面是一个边长0.5米的正方形,这块石料的横截面面积是多少平方米?体积是多少立方米?
0.5×0.5=0.25(m?)
0.25×3=0.75(m?)
答:这块石料的横截面面积是0.25m?。
体积是0.75m?。
0.5m
3m
1、商店有一个长方体的货柜,长是2.4米,宽是0.5米,高1.8米,这排货柜所占的空间是多少立方米?
2.4×0.5×1.8=
2.16(m?)
答:这个货柜所占的空间是2.16立方米.
巩固与联系
2、一个长方体粮仓,从里面量底面积是10.5平方米,粮食高1.1米,如果每立方米粮食重1.67吨,这个粮仓的粮食大约多少吨?(得数保留两位小数)
10.5×1.1×1.67≈19.29(吨)
答:这个粮仓的粮食大约19.29吨.
3、老李头给家院子挖了个长方体水池,长8.5米,宽5米,挖出来51立方米的泥土,这个水池有多深?
51÷(8.5×5)=1.2
答:水池深1.2米。
4、小康村修筑一条长100米,宽6米的马路,先铺上180立方米的渣土,渣土铺了有多厚?如果再铺上0.06米厚的混凝土,需要混凝土多少立方米?
180÷(100×6)=0.3(米)
答:渣土铺了0.3米厚。
100×6×0.06=36(立方米)
答:需要混凝土36立方米。
本课总结
同学们,说说看这节课你有什么收获?你又知道了什么?回家后请你选择你家中的正方体物品和长方体物品,测量它们的长、宽、高,计算出它们的体积是多少吧!相信你会越来越喜欢数学的。
本课结束
长方体和正方体体积的统一公式
苏教版六年级上
教学目标
让学生在具体情境中经历比较、分析、验证、归纳的过程,掌握长方体(正方体)的体积等于底面积乘高的计算方法。
使学生在活动中进一步积累空间与图形的学习经验,增强空间观念,发展数学思维。
使学生进一步体会图形与实际生活的联系,感受图形学习的价值,提高对数学的兴趣和对生活的热爱。
复习导入
同学们,我们学过了长方体和正方体的特征及表面积,请同学们分小组找出这两个图形的底面,分别是哪两个面?
底面
底面
复习导入
这两个图形的底面积是哪个面的面积?
就是长方体和正方体底面的面积
底面
底面
长方体和正方体底面的面积,叫做它们的底面积。
怎样计算长方体和正方体的底面积?
长方体的底面积=长×宽
正方体的底面积=棱长×棱长
我们前面学习的长方体和正方体体积是如何计算的?
新授知识
长方体的体积是长乘宽乘高,用字母表示V=abh
正方体的体积是棱长乘棱长乘棱长等于棱长的立方,用字母表示V=a?
长
宽
高
长方体和正方体的体积也可以,这样来计算
长方体的体积=底面积×高
底面
接下来请同学们,在小组中讨论讨论为什么可以这样来计算长方体和正方体的体积?
讨论与交流
长方体的体积=底面积×高
我是这样想的,长方体的长乘宽就是长方体的底面积,所以长方体的体积计算公式可以写成“长方体的体积=底面积×高”
讨论与交流
长方体的体积=底面积×高
如果用s表示底面积,那么长方体和正方体的体积还可以怎样表示,请同学尝试用字母表示这个公式。
因为长方体的长乘宽就是长方体的底面积,所以字母公式中把ab改成S就行了,也就是V=Sh
把aa换成S,另外一个棱也可以看成是高,也可以用V=Sh表示
分析与比较
1、先计算长方体和正方体的底面积,再计算它们的体积。
10m
8m
26m
4cm
4cm
4cm
底面积=4×4=16(cm?)
底面积=10×8=80(m?)
体积=16×4=64(cm?)
体积=80×26=2080(m?)
2、一个长方体底面积是16平方厘米,高是5厘米,求它的体积。
16×5=80(cm?)
底面积16cm?
3、一块长方体石料,长3米横截面是一个边长0.5米的正方形,这块石料的横截面面积是多少平方米?体积是多少立方米?
0.5×0.5=0.25(m?)
0.25×3=0.75(m?)
答:这块石料的横截面面积是0.25m?。
体积是0.75m?。
0.5m
3m
1、商店有一个长方体的货柜,长是2.4米,宽是0.5米,高1.8米,这排货柜所占的空间是多少立方米?
2.4×0.5×1.8=
2.16(m?)
答:这个货柜所占的空间是2.16立方米.
巩固与联系
2、一个长方体粮仓,从里面量底面积是10.5平方米,粮食高1.1米,如果每立方米粮食重1.67吨,这个粮仓的粮食大约多少吨?(得数保留两位小数)
10.5×1.1×1.67≈19.29(吨)
答:这个粮仓的粮食大约19.29吨.
3、老李头给家院子挖了个长方体水池,长8.5米,宽5米,挖出来51立方米的泥土,这个水池有多深?
51÷(8.5×5)=1.2
答:水池深1.2米。
4、小康村修筑一条长100米,宽6米的马路,先铺上180立方米的渣土,渣土铺了有多厚?如果再铺上0.06米厚的混凝土,需要混凝土多少立方米?
180÷(100×6)=0.3(米)
答:渣土铺了0.3米厚。
100×6×0.06=36(立方米)
答:需要混凝土36立方米。
本课总结
同学们,说说看这节课你有什么收获?你又知道了什么?回家后请你选择你家中的正方体物品和长方体物品,测量它们的长、宽、高,计算出它们的体积是多少吧!相信你会越来越喜欢数学的。
本课结束
