人教版 九年级上册数学 第23章旋转章末检测题 (word版,含答案)
文档属性
| 名称 | 人教版 九年级上册数学 第23章旋转章末检测题 (word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 466.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 09:28:35 | ||
图片预览

文档简介
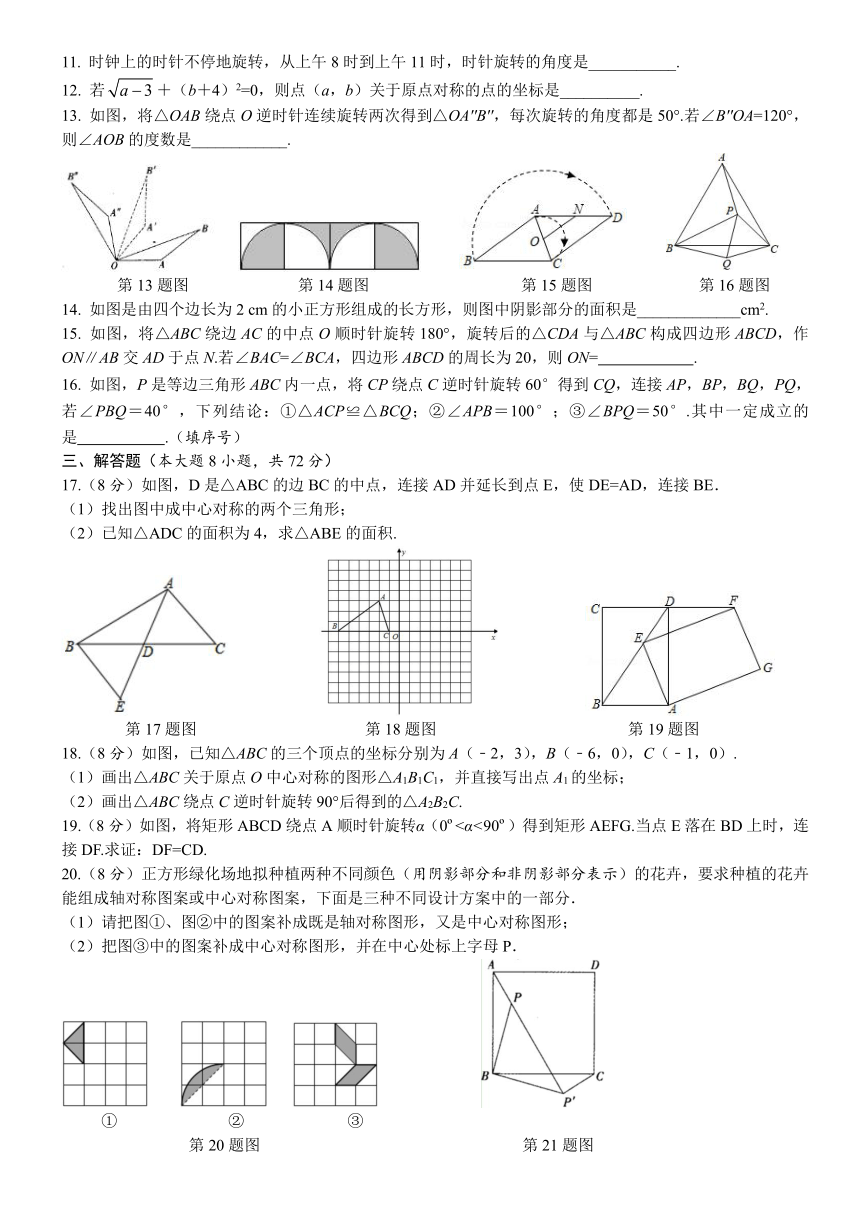
旋转章末检测卷
(本试卷满分120分)
一、选择题(本大题10小题,每小题3分,共30分)
1.
下列地铁标志图案中,既是轴对称图形又是中心对称图形的是( )
A
B
C
D
2.
在平面直角坐标系xOy中,点的坐标是(3,-2),点与点关于原点O对称,则点的坐标是( )
A.(3,-2)
B.(3,2)
C.(-3,2)
D.(-3,-2)
3.
如图,在△ABC中,∠BAC=30°,将△ABC绕点A顺时针旋转得到△AB′C′,则∠BAC′的度数为( )
A.
30°
B.
35°
C.
32.5°
D.
65°
第3题图
第4题图
第5题图
第6题图
4.
如图为某汽车轮毂图案,将图案绕中心旋转下列角度,能与原来图案重合的是( )
A.
36°
B.
60°
C.
72°
D.
90°
5.
如图,已知△ABC与△A′B′C′成中心对称,则下列说法不正确的是( )
A.
AB=A′B′,BC=B′C′
B.
BC∥B′C′
C.
S△AOB=S△A′OB′
D.
△ABC≌△A′OC′
6.
如图,将△ABC绕点A逆时针旋转得到△ADE.若点D在线段BC的延长线上,则∠ADE的度数为( )
A.
B.
C.
D.
7.
如图,线段AB与线段CD关于点P中心对称,若点A(a,b),B(5,1),D(﹣3,﹣1),则点C的坐标为( )
A.(﹣a,﹣b)
B.(﹣a+2,﹣b)
C.(﹣a﹣1,﹣b+1)
D.(﹣a+1,﹣b﹣1)
(?http:?/??/?www.?/?"
\o
"中国教育出版网\"
?)
第7题图
第8题图
第9题图
第10题图
8.
如图,在4×4的网格纸中,△ABC的三个顶点都在格点上,现要在这张网格纸的四个格点M,N,P,Q中找一点作为旋转中心.将△ABC绕着这个中心进行旋转,旋转前后的两个三角形成中心对称,且旋转后的三角形的三个顶点都在网格纸的格点上,那么满足条件的旋转中心有( )
A.
点M,点N
B.
点M,点Q
C.
点N,点P
D.
点P,点Q
9.
如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,AD∥x轴,AD=4,∠A=60°.将菱形ABCD绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是( )
A.
B.
(2,﹣4)
C.
D.
或
10.
在平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1中心对称,再作△B2A3B3与△B2A2B1关于点B2中心对称…如此作下去,则△B2020A2021B2021的顶点A2021的坐标是( )
A.
B.
C.
D.
二、填空题(本大题6小题,每小题3分,共18分)
11.
时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是___________.
12.
若+(b+4)2=0,则点(a,b)关于原点对称的点的坐标是__________.
13.
如图,将△OAB绕点O逆时针连续旋转两次得到△OA′′B′′,每次旋转的角度都是50°.若∠B′′OA=120°,则∠AOB的度数是____________.
第13题图
第14题图
第15题图
第16题图
14.
如图是由四个边长为2
cm的小正方形组成的长方形,则图中阴影部分的面积是_____________cm2.
15.
如图,将△ABC绕边AC的中点O顺时针旋转180°,旋转后的△CDA与△ABC构成四边形ABCD,作ON∥AB交AD于点N.若∠BAC=∠BCA,四边形ABCD的周长为20,则ON=
.
16.
如图,P是等边三角形ABC内一点,将CP绕点C逆时针旋转60°得到CQ,连接AP,BP,BQ,PQ,若∠PBQ=40°,下列结论:①△ACP≌△BCQ;②∠APB=100°;③∠BPQ=50°.其中一定成立的是
.(填序号)
三、解答题(本大题8小题,共72分)
17.(8分)如图,D是△ABC的边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)找出图中成中心对称的两个三角形;
(2)已知△ADC的面积为4,求△ABE的面积.
第17题图
第18题图
第19题图
18.(8分)如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)画出△ABC关于原点O中心对称的图形△A1B1C1,并直接写出点A1的坐标;
(2)画出△ABC绕点C逆时针旋转90°后得到的△A2B2C.
19.(8分)如图,将矩形ABCD绕点A顺时针旋转α(0?<α<90?)得到矩形AEFG.当点E落在BD上时,连接DF.求证:DF=CD.
20.(8分)正方形绿化场地拟种植两种不同颜色(用阴影部分和非阴影部分表示)的花卉,要求种植的花卉能组成轴对称图案或中心对称图案,下面是三种不同设计方案中的一部分.
(1)请把图①、图②中的图案补成既是轴对称图形,又是中心对称图形;
(2)把图③中的图案补成中心对称图形,并在中心处标上字母P.
①
②
③
第20题图
第21题图
21.(8分)如图,四边形ABCD是正方形,P是正方形内任意一点,连接PA,PB,将△PAB绕点B顺时针旋转至△P′CB处.
(1)猜想△PBP′的形状,并说明理由;
(2)若PP′=cm,求S△PBP′.
22.(10分)阅读下面操作过程,回答问题:
在一次数学实践探究活动中,李小明同学过AB,CD的中点作直线EF(如图①所示),将矩形ABCD分割成a,b两部分;王小刚同学经过A,C两点作直线AC(如图②所示),将矩形ABCD分割成c,d两部分.
(1)若a部分的面积为Sa,b部分的面积为Sb,c部分的面积为Sc
,d部分的面积为Sd,则它们的面积关系是Sa
Sb
Sc
Sd;(填“>”“<”或“=”)
(2)根据这两位同学的分割原理,你能探索出多少种分割方法?请任意画出一种;
(3)由上述的实践操作过程,你能发现什么规律?
①
②
③
第22题图
23.(11分)已知P为线段AB上一点,将线段AP绕点A逆时针旋转,得到线段AC;再将线段BP绕点B逆时针旋转,得到线段BD;连接AD,取AD的中点M,连接BM,CM.
(1)如图①,当点P在线段CM上时,求证:PM∥BD;
(2)如图②,当点P不在线段CM上时,CM交AB于点F,写出线段BM与CM的数量关系与位置关系,并证明.
①
②
第23题图
24.(11分)如图①,在△ABC中,∠A=90°,AB=AC=,点D,E分别在边AB,AC上,且AD=AE=2-,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),分别连接CE,BD.
(1)如图②,当0°<α<90°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
(3)连接CD,在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
①
②
③
第24题图
旋转章末检测卷
一、1.
D
2.
C
3.
B
4.
C
5.
D
6.
D
7.
B
8.
C
9.
D
10.
A
二、11.
90°
12.(-3,4)
13.
20°
14.
8
15.
2.5
16.
①②
三、17.
解:(1)△ADC与△EDB成中心对称.
(2)由(1),得△ADC≌△EDB.因为△ADC的面积为4,所以△EDB的面积为4.
因为D为BC的中点,所以△ABD的面积为4.所以△ABE的面积为8.
18.
解:(1)如图,△A1B1C1即为所求作,点A1的坐标为(2,﹣3).
第18题图
(2)如图,△A2B2C即为所求作.
19.
证明:因为四边形ABCD为矩形,所以AD=BC,AB=CD,∠BAD=∠ABC=90°.
因为矩形ABCD绕点A顺时针旋转α(0?<α<90?)得矩形AEFG,所以AE=AB,EF=BC,∠AEF=∠ABC=90°.
所以EF=DA,∠AEB=∠ABE.
因为∠ABE
+∠ADE=90?,∠AEB+∠DEF=90?,所以∠DEF=∠ADE.所以∠AED=∠FDE.
所以△AED≌△FDE.所以AE=FD.所以DF=CD.
20.
解:(1)(2)(3)答案不唯一,下列图形供参考.
第20题图
21.
解:(1)△PBP′是等腰直角三角形.
理由:因为△PAB绕点B顺时针旋转至△P′CB处,所以BP′=BP,∠CBP′=∠ABP.
因为四边形ABCD是正方形,所以∠ABC=90°.所以∠ABP+∠PBC=90°.
所以∠CBP′+∠PBC=90°,即∠PBP′=90°.所以△PBP′是等腰直角三角形.
(2)因为PP′=cm,所以点B到PP′的距离为PP′=×=(cm).
所以S△PBP′=××=2(cm).
22.
解:(1)=
=
=
(2)无数种.图略.(过对角线交点的直线)
(3)过中心对称图形的对称中心的任意一条直线,都可以把图形分割成面积相等的两部分.
23.
解:(1)由题意,得∠CAP=60°,且AC=AP,所以△APC是等边三角形.所以∠APC=60°.所以∠BPM=60°.
因为∠PBD=120°,所以∠BPM+∠PBD=180°.所以PM∥BD.
(2)CM⊥BM,CM=BM.
证明:如图,延长BM至点G,使得MG=MB,连接AG,BC,GC,PC,GD.
因为AM=MD,GM=BM,所以四边形AGDB是平行四边形.
所以AG=BD,AG∥BD.所以∠BAG=180?-∠ABD=60?.所以∠CAG=120?.
因为△APC是等边三角形,所以AC=CP,∠CPB=120?.
因为PB=DB=AG,所以△CAG≌△CPB.
所以CG=CB,∠ACG=∠PCB.所以∠GCB=60?.所以△CBG是等边三角形.
因为GM=BM,所以CM⊥BM.所以∠CMB=90?,∠MCB=30?.所以CB=2BM.所以CM==BM.
第23题图
24.(1)证明:根据题意,得AB=AC,AD=AE,∠CAE=∠BAD.所以△ACE≌△ABD.所以CE=BD.
(2)证明:根据题意,得AB=AC,AD=AE,∠CAB=∠EAD=90°.所以△ACE≌△ABD.所以∠ACE=∠ABD.
因为∠ACE+∠AEC=90°,且∠AEC=∠FEB,所以∠ABD+∠FEB=90°.所以∠EFB=90°.所以CF⊥BD.
因为AB=AC=,AD=AE=2-,∠CAB=∠EAD=90°,所以BC=2,CD=AC+AD=2.所以BC=CD.
因为CF⊥BD,所以CF垂直平分BD.
(3)解:在△BCD中,边BC的长是定值,所以当BC边上的高的值最大时,△BCD的面积有最大值.
所以当点D在线段BC的垂直平分线上时,△BCD的面积取得最大值,如图所示.
因为AB=AC=,AD=AE=2-,∠CAB=∠EAD=90°,DG⊥BC于点G,所以AG=BC=1,∠GAB=45°.
所以DG=AG+AD=3-,∠DAB=180°-45°=135°.
所以△BCD面积的最大值为BC?DG=×2×(3-)=3-,旋转角α=135°.
第24题图
C
A
B
D
F
M
P
C
A
B
D
F
M
G
P
(本试卷满分120分)
一、选择题(本大题10小题,每小题3分,共30分)
1.
下列地铁标志图案中,既是轴对称图形又是中心对称图形的是( )
A
B
C
D
2.
在平面直角坐标系xOy中,点的坐标是(3,-2),点与点关于原点O对称,则点的坐标是( )
A.(3,-2)
B.(3,2)
C.(-3,2)
D.(-3,-2)
3.
如图,在△ABC中,∠BAC=30°,将△ABC绕点A顺时针旋转得到△AB′C′,则∠BAC′的度数为( )
A.
30°
B.
35°
C.
32.5°
D.
65°
第3题图
第4题图
第5题图
第6题图
4.
如图为某汽车轮毂图案,将图案绕中心旋转下列角度,能与原来图案重合的是( )
A.
36°
B.
60°
C.
72°
D.
90°
5.
如图,已知△ABC与△A′B′C′成中心对称,则下列说法不正确的是( )
A.
AB=A′B′,BC=B′C′
B.
BC∥B′C′
C.
S△AOB=S△A′OB′
D.
△ABC≌△A′OC′
6.
如图,将△ABC绕点A逆时针旋转得到△ADE.若点D在线段BC的延长线上,则∠ADE的度数为( )
A.
B.
C.
D.
7.
如图,线段AB与线段CD关于点P中心对称,若点A(a,b),B(5,1),D(﹣3,﹣1),则点C的坐标为( )
A.(﹣a,﹣b)
B.(﹣a+2,﹣b)
C.(﹣a﹣1,﹣b+1)
D.(﹣a+1,﹣b﹣1)
(?http:?/??/?www.?/?"
\o
"中国教育出版网\"
?)
第7题图
第8题图
第9题图
第10题图
8.
如图,在4×4的网格纸中,△ABC的三个顶点都在格点上,现要在这张网格纸的四个格点M,N,P,Q中找一点作为旋转中心.将△ABC绕着这个中心进行旋转,旋转前后的两个三角形成中心对称,且旋转后的三角形的三个顶点都在网格纸的格点上,那么满足条件的旋转中心有( )
A.
点M,点N
B.
点M,点Q
C.
点N,点P
D.
点P,点Q
9.
如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,AD∥x轴,AD=4,∠A=60°.将菱形ABCD绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是( )
A.
B.
(2,﹣4)
C.
D.
或
10.
在平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1中心对称,再作△B2A3B3与△B2A2B1关于点B2中心对称…如此作下去,则△B2020A2021B2021的顶点A2021的坐标是( )
A.
B.
C.
D.
二、填空题(本大题6小题,每小题3分,共18分)
11.
时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是___________.
12.
若+(b+4)2=0,则点(a,b)关于原点对称的点的坐标是__________.
13.
如图,将△OAB绕点O逆时针连续旋转两次得到△OA′′B′′,每次旋转的角度都是50°.若∠B′′OA=120°,则∠AOB的度数是____________.
第13题图
第14题图
第15题图
第16题图
14.
如图是由四个边长为2
cm的小正方形组成的长方形,则图中阴影部分的面积是_____________cm2.
15.
如图,将△ABC绕边AC的中点O顺时针旋转180°,旋转后的△CDA与△ABC构成四边形ABCD,作ON∥AB交AD于点N.若∠BAC=∠BCA,四边形ABCD的周长为20,则ON=
.
16.
如图,P是等边三角形ABC内一点,将CP绕点C逆时针旋转60°得到CQ,连接AP,BP,BQ,PQ,若∠PBQ=40°,下列结论:①△ACP≌△BCQ;②∠APB=100°;③∠BPQ=50°.其中一定成立的是
.(填序号)
三、解答题(本大题8小题,共72分)
17.(8分)如图,D是△ABC的边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)找出图中成中心对称的两个三角形;
(2)已知△ADC的面积为4,求△ABE的面积.
第17题图
第18题图
第19题图
18.(8分)如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)画出△ABC关于原点O中心对称的图形△A1B1C1,并直接写出点A1的坐标;
(2)画出△ABC绕点C逆时针旋转90°后得到的△A2B2C.
19.(8分)如图,将矩形ABCD绕点A顺时针旋转α(0?<α<90?)得到矩形AEFG.当点E落在BD上时,连接DF.求证:DF=CD.
20.(8分)正方形绿化场地拟种植两种不同颜色(用阴影部分和非阴影部分表示)的花卉,要求种植的花卉能组成轴对称图案或中心对称图案,下面是三种不同设计方案中的一部分.
(1)请把图①、图②中的图案补成既是轴对称图形,又是中心对称图形;
(2)把图③中的图案补成中心对称图形,并在中心处标上字母P.
①
②
③
第20题图
第21题图
21.(8分)如图,四边形ABCD是正方形,P是正方形内任意一点,连接PA,PB,将△PAB绕点B顺时针旋转至△P′CB处.
(1)猜想△PBP′的形状,并说明理由;
(2)若PP′=cm,求S△PBP′.
22.(10分)阅读下面操作过程,回答问题:
在一次数学实践探究活动中,李小明同学过AB,CD的中点作直线EF(如图①所示),将矩形ABCD分割成a,b两部分;王小刚同学经过A,C两点作直线AC(如图②所示),将矩形ABCD分割成c,d两部分.
(1)若a部分的面积为Sa,b部分的面积为Sb,c部分的面积为Sc
,d部分的面积为Sd,则它们的面积关系是Sa
Sb
Sc
Sd;(填“>”“<”或“=”)
(2)根据这两位同学的分割原理,你能探索出多少种分割方法?请任意画出一种;
(3)由上述的实践操作过程,你能发现什么规律?
①
②
③
第22题图
23.(11分)已知P为线段AB上一点,将线段AP绕点A逆时针旋转,得到线段AC;再将线段BP绕点B逆时针旋转,得到线段BD;连接AD,取AD的中点M,连接BM,CM.
(1)如图①,当点P在线段CM上时,求证:PM∥BD;
(2)如图②,当点P不在线段CM上时,CM交AB于点F,写出线段BM与CM的数量关系与位置关系,并证明.
①
②
第23题图
24.(11分)如图①,在△ABC中,∠A=90°,AB=AC=,点D,E分别在边AB,AC上,且AD=AE=2-,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),分别连接CE,BD.
(1)如图②,当0°<α<90°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
(3)连接CD,在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
①
②
③
第24题图
旋转章末检测卷
一、1.
D
2.
C
3.
B
4.
C
5.
D
6.
D
7.
B
8.
C
9.
D
10.
A
二、11.
90°
12.(-3,4)
13.
20°
14.
8
15.
2.5
16.
①②
三、17.
解:(1)△ADC与△EDB成中心对称.
(2)由(1),得△ADC≌△EDB.因为△ADC的面积为4,所以△EDB的面积为4.
因为D为BC的中点,所以△ABD的面积为4.所以△ABE的面积为8.
18.
解:(1)如图,△A1B1C1即为所求作,点A1的坐标为(2,﹣3).
第18题图
(2)如图,△A2B2C即为所求作.
19.
证明:因为四边形ABCD为矩形,所以AD=BC,AB=CD,∠BAD=∠ABC=90°.
因为矩形ABCD绕点A顺时针旋转α(0?<α<90?)得矩形AEFG,所以AE=AB,EF=BC,∠AEF=∠ABC=90°.
所以EF=DA,∠AEB=∠ABE.
因为∠ABE
+∠ADE=90?,∠AEB+∠DEF=90?,所以∠DEF=∠ADE.所以∠AED=∠FDE.
所以△AED≌△FDE.所以AE=FD.所以DF=CD.
20.
解:(1)(2)(3)答案不唯一,下列图形供参考.
第20题图
21.
解:(1)△PBP′是等腰直角三角形.
理由:因为△PAB绕点B顺时针旋转至△P′CB处,所以BP′=BP,∠CBP′=∠ABP.
因为四边形ABCD是正方形,所以∠ABC=90°.所以∠ABP+∠PBC=90°.
所以∠CBP′+∠PBC=90°,即∠PBP′=90°.所以△PBP′是等腰直角三角形.
(2)因为PP′=cm,所以点B到PP′的距离为PP′=×=(cm).
所以S△PBP′=××=2(cm).
22.
解:(1)=
=
=
(2)无数种.图略.(过对角线交点的直线)
(3)过中心对称图形的对称中心的任意一条直线,都可以把图形分割成面积相等的两部分.
23.
解:(1)由题意,得∠CAP=60°,且AC=AP,所以△APC是等边三角形.所以∠APC=60°.所以∠BPM=60°.
因为∠PBD=120°,所以∠BPM+∠PBD=180°.所以PM∥BD.
(2)CM⊥BM,CM=BM.
证明:如图,延长BM至点G,使得MG=MB,连接AG,BC,GC,PC,GD.
因为AM=MD,GM=BM,所以四边形AGDB是平行四边形.
所以AG=BD,AG∥BD.所以∠BAG=180?-∠ABD=60?.所以∠CAG=120?.
因为△APC是等边三角形,所以AC=CP,∠CPB=120?.
因为PB=DB=AG,所以△CAG≌△CPB.
所以CG=CB,∠ACG=∠PCB.所以∠GCB=60?.所以△CBG是等边三角形.
因为GM=BM,所以CM⊥BM.所以∠CMB=90?,∠MCB=30?.所以CB=2BM.所以CM==BM.
第23题图
24.(1)证明:根据题意,得AB=AC,AD=AE,∠CAE=∠BAD.所以△ACE≌△ABD.所以CE=BD.
(2)证明:根据题意,得AB=AC,AD=AE,∠CAB=∠EAD=90°.所以△ACE≌△ABD.所以∠ACE=∠ABD.
因为∠ACE+∠AEC=90°,且∠AEC=∠FEB,所以∠ABD+∠FEB=90°.所以∠EFB=90°.所以CF⊥BD.
因为AB=AC=,AD=AE=2-,∠CAB=∠EAD=90°,所以BC=2,CD=AC+AD=2.所以BC=CD.
因为CF⊥BD,所以CF垂直平分BD.
(3)解:在△BCD中,边BC的长是定值,所以当BC边上的高的值最大时,△BCD的面积有最大值.
所以当点D在线段BC的垂直平分线上时,△BCD的面积取得最大值,如图所示.
因为AB=AC=,AD=AE=2-,∠CAB=∠EAD=90°,DG⊥BC于点G,所以AG=BC=1,∠GAB=45°.
所以DG=AG+AD=3-,∠DAB=180°-45°=135°.
所以△BCD面积的最大值为BC?DG=×2×(3-)=3-,旋转角α=135°.
第24题图
C
A
B
D
F
M
P
C
A
B
D
F
M
G
P
同课章节目录
