湘教版七上数学1.1具有相反意义的量 课件(共30张PPT)
文档属性
| 名称 | 湘教版七上数学1.1具有相反意义的量 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
1.1
具有相反意义的量
湘教版
七年级上
教学目标
1.
理解具有相反意义的量的含义及其表示方法;
2.
能用正数或负数表示实际问题中具有相反意义的量;
3.
能把学过的数进行分类,并归纳抽象出有理数的概念;
4.
了解数是在生产生活中产生和发展的。
新知导入
你能举例说出我们在小学学过哪些数吗?
0,1,2,12,100,……这些是我们学过的自然数。
0.1,1.5,2.33…,3.1,……
这些是我们学过的小数。
我们还学过分数,如
……
新知导入
数是人们在日常生产生活实践中产生并不断发展的,由于记物体的个数和表示物体的顺序的需要,产生了自然数;由于度量时,需要表示不是“整米”等的数,产生了小数和分数。有了数,我们可以进行数的运算。
那么,我们在日常生产和生活实践中,还需要什么数吗?
新知讲解
下图中温度计上是如何区分零上的度数和零下的度数的?
零上的度数用红色表示,
零下的度数用蓝色表示。
新知讲解
零上34℃比零下20℃高多少度?显然,如果仅用颜
色来区分,就列不出便于计算的算式.因此我们必须想其
他的方法.
新知讲解
(1)在预报北京市某天的天气时,播音员说:“北京,晴,局部多云,零下6摄氏度到5摄氏度.”这时,屏幕上是如何显示这天的温度的?
屏幕上显示“-6~5℃”。
例题讲解
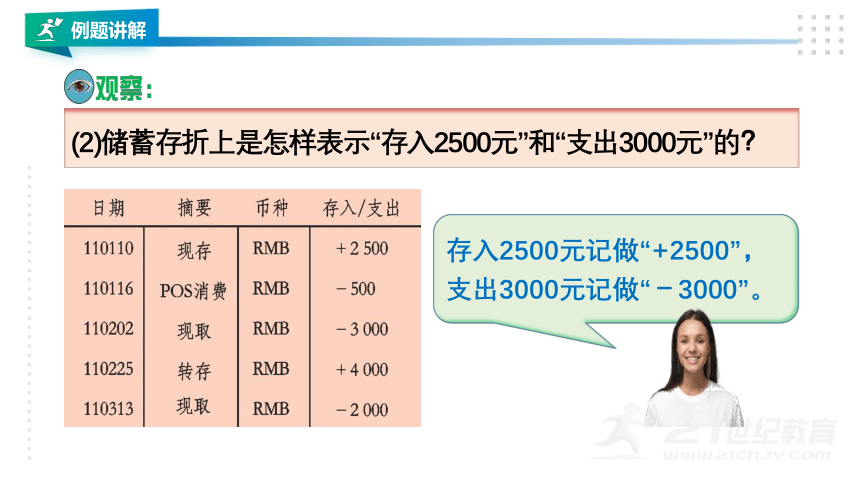
(2)储蓄存折上是怎样表示“存入2500元”和“支出3000元”的?
存入2500元记做“+2500”,
支出3000元记做“-3000”。
例题讲解
温度的“零上5摄氏度”与“零下6摄氏度”、储蓄中的“存入2
500元”与“支出3
000元”分别是一对相反意义的量.
为了便于区分意义相反的量,数学上规定:
在具有相反意义的一对量中,我们把其中的一种量用正数表示,而另一种量就用负数表示,它是在正数前面加上“-”(读作负)号的数.
新知讲解
你能举出正数、负数的例子吗?
例如3,125,10.5,
等大于0的自然数和分数(或小数)就是正数.
例如-3,-14,-0.618,
等在正数前面加上“-”的数就是负数.
有的时候在正数前面加上“+”(读作正)号,以强调它是正数.例如,“正数5”写作“+5”,但通常把“+”号省略不写.
新知讲解
想一想:0是正数吗?
0既不是正数,也不是负数.
我们也把正数和0统称为非负数.
新知讲解
(2)储蓄存折上是怎样表示“存入2500元”和“支出3000元”的?
海平面以上与海平面以下表示的意义相反.海平面以上1025m记做“1025m”,海平面以下155m记做“-155m”.
新知讲解
在东西向的马路上,把出发点记为0,向东与向西意义相反.若把向东走2km记做“2km”,那么向西走2.6km
应记做“-2.6km”.
新知讲解
新知讲解
请你举例说明从小学到现在,我们学过的数有哪些?
自然数:0,1,2,3,4,…
小数:
3.2,
,
5.33,…;
分数:
,
,
,…
负数:-3,-100,-0.125,
,
,…
新知讲解
因此,有限小数或无限循环小数其实就是分数.
分数可以化成有限小数或无限循环小数.
例如:
有限小数或无限循环小数也可以化为分数.
例如:
新知讲解
你能对我们学过的数进行分类吗?
负分数
-0.125
…
负整数
-3,-1,-155,…
正分数
0.6
…
正整数
1,3,167,…
0
有理数
新知讲解
在我们学过的数中,我们规定:
正整数、零和负整数统称为整数.
正分数和负分数统称为分数.
整数和分数统称为有理数.
巩固练习
1.
下列说法正确的是
(
)
A.
0既不是正数,也不是负数
B.
所有小数都是有理数
C.
一个数前面加上“-”号后得到的数是负数
D.
有理数包括正数和负数
A
巩固练习
2.
李阿姨的小吃店星期一盈利500元,星期五亏本50元.若
把盈利500元记作+500元,那么亏本50元记作(
)
A.
+50元
B.
-50元
C.
+450元
D.
-500元
B
巩固练习
3.
下列各数中,属于正有理数的是
(
)
A.
0
B.
3.14
C.
π
D.
-9
B
4.
在有理数-2,3.7,-2.01,1,0
,47%中,正整数和负分数的个数分别是
(
)
A.
1,1
B.
1,2
C.
2
,1
D.
2,2
A
巩固练习
巩固练习
5.
在一袋大米上标注:“净含量:20±0.5kg”,这里的
“+”表示
,
“-”表示
。
比标准质量超过的kg数范围
比标准质量不足的kg数范围
课堂总结
1.
如何用数表示具有相反意义的一对量?
在具有相反意义的一对量中,把其中的一种量用正数表示,
另一种量就用负数表示。在正数前面加上“-”号就是负数。
板书设计
2.
有理数如何分类?
有理数
整数
零
分数
正整数
负整数
正分数
负分数
课堂总结
因为正整数、正分数都是正有理数,负整数、负分数都是负有理数,所以,有理数还可分为正有理数、零、负有理数三大类,其中正有理数和零又称非负数。
作业布置
1.
回答下列问题:
(1)通常把水结冰时的温度规定为0℃,那么比水结冰时的温度低5℃应记做什么?
(2)如果在东西向的马路上把出发点记为0,把向东走的路程记做正数,那么走-50m是什么意思?
作业布置
解:(1)通常把0℃以上的温度记作正数,0℃以下的温度记作负数,比水结冰时的温度低5℃是0℃以下的温度,故应记做-5℃。
(2)向东走的路程与向西走的路程是具有相反的量,因为把向东走的路程记作正数,则向西走的路程记作负数.-50是负数,所以-50m.表示向西走50m.
作业布置
2.
下列数:
3.6,
,-78,0,-0.37,9,-5.14,-1。其中
整数:
;
分数:
.
﹣78,0,9,﹣1
3.6,
,﹣0.37,﹣5.14
作业布置
3.
下列有理数中哪些是非负数?哪些是负数?
解:非负数有:
负数有:
解析:非负数包括正数和零,负数是正数前面加“-”的数.
https://www.21cnjy.com/help/help_extract.php
1.1
具有相反意义的量
湘教版
七年级上
教学目标
1.
理解具有相反意义的量的含义及其表示方法;
2.
能用正数或负数表示实际问题中具有相反意义的量;
3.
能把学过的数进行分类,并归纳抽象出有理数的概念;
4.
了解数是在生产生活中产生和发展的。
新知导入
你能举例说出我们在小学学过哪些数吗?
0,1,2,12,100,……这些是我们学过的自然数。
0.1,1.5,2.33…,3.1,……
这些是我们学过的小数。
我们还学过分数,如
……
新知导入
数是人们在日常生产生活实践中产生并不断发展的,由于记物体的个数和表示物体的顺序的需要,产生了自然数;由于度量时,需要表示不是“整米”等的数,产生了小数和分数。有了数,我们可以进行数的运算。
那么,我们在日常生产和生活实践中,还需要什么数吗?
新知讲解
下图中温度计上是如何区分零上的度数和零下的度数的?
零上的度数用红色表示,
零下的度数用蓝色表示。
新知讲解
零上34℃比零下20℃高多少度?显然,如果仅用颜
色来区分,就列不出便于计算的算式.因此我们必须想其
他的方法.
新知讲解
(1)在预报北京市某天的天气时,播音员说:“北京,晴,局部多云,零下6摄氏度到5摄氏度.”这时,屏幕上是如何显示这天的温度的?
屏幕上显示“-6~5℃”。
例题讲解
(2)储蓄存折上是怎样表示“存入2500元”和“支出3000元”的?
存入2500元记做“+2500”,
支出3000元记做“-3000”。
例题讲解
温度的“零上5摄氏度”与“零下6摄氏度”、储蓄中的“存入2
500元”与“支出3
000元”分别是一对相反意义的量.
为了便于区分意义相反的量,数学上规定:
在具有相反意义的一对量中,我们把其中的一种量用正数表示,而另一种量就用负数表示,它是在正数前面加上“-”(读作负)号的数.
新知讲解
你能举出正数、负数的例子吗?
例如3,125,10.5,
等大于0的自然数和分数(或小数)就是正数.
例如-3,-14,-0.618,
等在正数前面加上“-”的数就是负数.
有的时候在正数前面加上“+”(读作正)号,以强调它是正数.例如,“正数5”写作“+5”,但通常把“+”号省略不写.
新知讲解
想一想:0是正数吗?
0既不是正数,也不是负数.
我们也把正数和0统称为非负数.
新知讲解
(2)储蓄存折上是怎样表示“存入2500元”和“支出3000元”的?
海平面以上与海平面以下表示的意义相反.海平面以上1025m记做“1025m”,海平面以下155m记做“-155m”.
新知讲解
在东西向的马路上,把出发点记为0,向东与向西意义相反.若把向东走2km记做“2km”,那么向西走2.6km
应记做“-2.6km”.
新知讲解
新知讲解
请你举例说明从小学到现在,我们学过的数有哪些?
自然数:0,1,2,3,4,…
小数:
3.2,
,
5.33,…;
分数:
,
,
,…
负数:-3,-100,-0.125,
,
,…
新知讲解
因此,有限小数或无限循环小数其实就是分数.
分数可以化成有限小数或无限循环小数.
例如:
有限小数或无限循环小数也可以化为分数.
例如:
新知讲解
你能对我们学过的数进行分类吗?
负分数
-0.125
…
负整数
-3,-1,-155,…
正分数
0.6
…
正整数
1,3,167,…
0
有理数
新知讲解
在我们学过的数中,我们规定:
正整数、零和负整数统称为整数.
正分数和负分数统称为分数.
整数和分数统称为有理数.
巩固练习
1.
下列说法正确的是
(
)
A.
0既不是正数,也不是负数
B.
所有小数都是有理数
C.
一个数前面加上“-”号后得到的数是负数
D.
有理数包括正数和负数
A
巩固练习
2.
李阿姨的小吃店星期一盈利500元,星期五亏本50元.若
把盈利500元记作+500元,那么亏本50元记作(
)
A.
+50元
B.
-50元
C.
+450元
D.
-500元
B
巩固练习
3.
下列各数中,属于正有理数的是
(
)
A.
0
B.
3.14
C.
π
D.
-9
B
4.
在有理数-2,3.7,-2.01,1,0
,47%中,正整数和负分数的个数分别是
(
)
A.
1,1
B.
1,2
C.
2
,1
D.
2,2
A
巩固练习
巩固练习
5.
在一袋大米上标注:“净含量:20±0.5kg”,这里的
“+”表示
,
“-”表示
。
比标准质量超过的kg数范围
比标准质量不足的kg数范围
课堂总结
1.
如何用数表示具有相反意义的一对量?
在具有相反意义的一对量中,把其中的一种量用正数表示,
另一种量就用负数表示。在正数前面加上“-”号就是负数。
板书设计
2.
有理数如何分类?
有理数
整数
零
分数
正整数
负整数
正分数
负分数
课堂总结
因为正整数、正分数都是正有理数,负整数、负分数都是负有理数,所以,有理数还可分为正有理数、零、负有理数三大类,其中正有理数和零又称非负数。
作业布置
1.
回答下列问题:
(1)通常把水结冰时的温度规定为0℃,那么比水结冰时的温度低5℃应记做什么?
(2)如果在东西向的马路上把出发点记为0,把向东走的路程记做正数,那么走-50m是什么意思?
作业布置
解:(1)通常把0℃以上的温度记作正数,0℃以下的温度记作负数,比水结冰时的温度低5℃是0℃以下的温度,故应记做-5℃。
(2)向东走的路程与向西走的路程是具有相反的量,因为把向东走的路程记作正数,则向西走的路程记作负数.-50是负数,所以-50m.表示向西走50m.
作业布置
2.
下列数:
3.6,
,-78,0,-0.37,9,-5.14,-1。其中
整数:
;
分数:
.
﹣78,0,9,﹣1
3.6,
,﹣0.37,﹣5.14
作业布置
3.
下列有理数中哪些是非负数?哪些是负数?
解:非负数有:
负数有:
解析:非负数包括正数和零,负数是正数前面加“-”的数.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
