湘教版七上数学1.4.1有理数的加法(1) 课件(共27张PPT)
文档属性
| 名称 | 湘教版七上数学1.4.1有理数的加法(1) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 13:04:42 | ||
图片预览






文档简介
(共29张PPT)
1.4.1
有理数的加法(1)
湘教版
七年级上
教学目标
1.
理解、记住有理数的三条加法法则;
2.
能正确地根据有理数的加法法则进行运算;
3.
通过观察、计算,培养思维的灵活性,计算的严谨性.
新知导入
我们已经会计算两个非负数的和,即计算两个正数之和,0与正数之和,如8+12=20,3.75+0.25=4,0+2.3=2.3。
下面的加法算式与两个非负数的和有何不同?
(-4)+(﹣3)
(-4)+21
8+(-10)
0+(-7)
如何计算含有负数的有理数的加法呢?
新知讲解
如何计算两个负数的和?
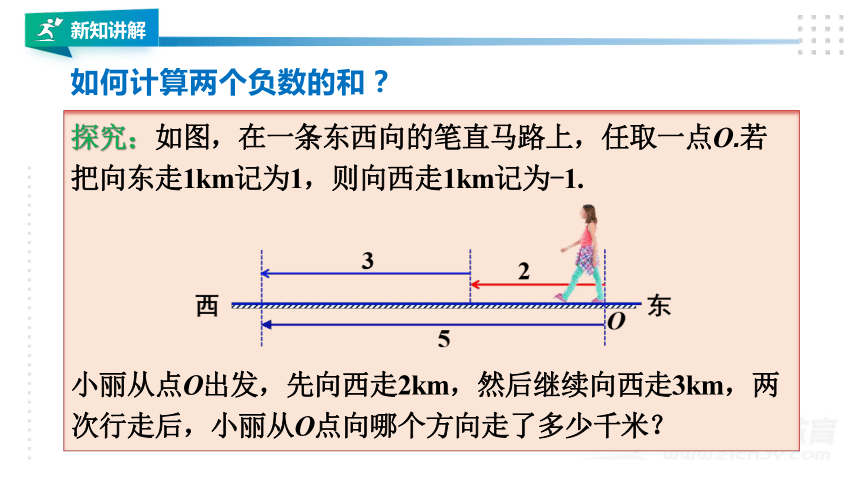
探究:如图,在一条东西向的笔直马路上,任取一点O.若把向东走1km记为1,则向西走1km记为-1.
小丽从点O出发,先向西走2km,然后继续向西走3km,两次行走后,小丽从O点向哪个方向走了多少千米?
新知讲解
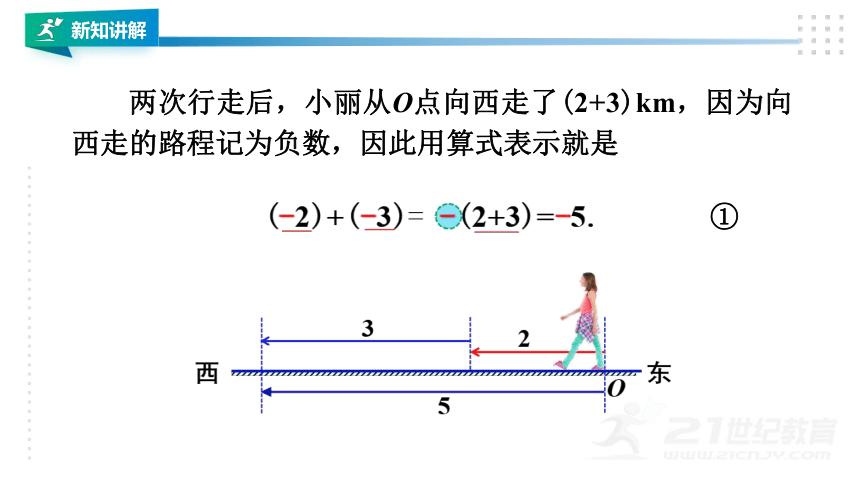
两次行走后,小丽从O点向西走了(2+3)km,因为向西走的路程记为负数,因此用算式表示就是
①
新知讲解
两个负数相加,结果是负数,并且把它们的绝对值相加.
由①式得到启发,数学上规定:
新知讲解
例1
计算:
(1)
(-8)+(-12);
(2)
(-3.75)+(-0.25).
解:(1)
(-8)+(-12)=
-(8+12)
=-20;
(2)
(-3.75)+(-0.25)
=-(3.75+0.25)
=-4.
合作探究
如何求一个正数与一个负数的和?
探究:在一条东西向的笔直马路上,任取一点O.若把向东走1km记为1,则向西走1km记为-1。
(1)小亮从O点出发,先向东走了4km,然后掉头向西走1km,小亮两次行走的效果等于从点O向哪个方向走了多少米?
(2)小刚从点O出发,先向东走了1km,然后掉头向西走3km,小刚两次行走的效果等于从点O向哪个方向走了多少米?
合作探究
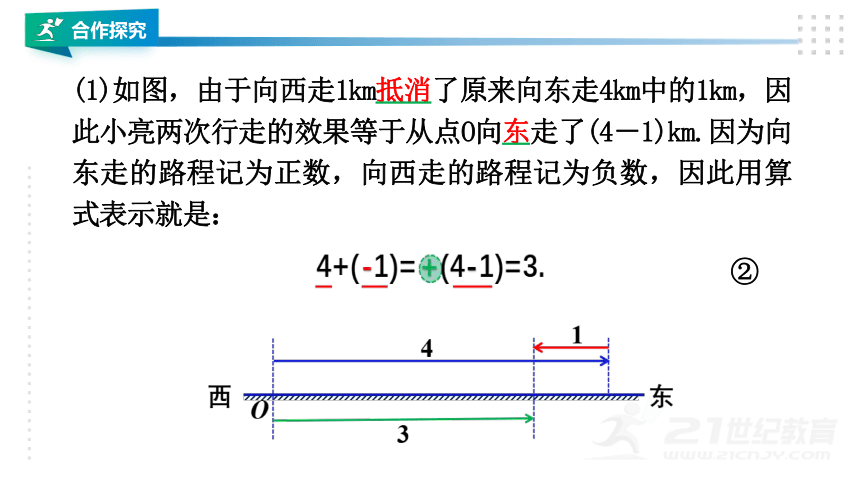
(1)如图,由于向西走1km抵消了原来向东走4km中的1km,因此小亮两次行走的效果等于从点O向东走了(4-1)km.因为向东走的路程记为正数,向西走的路程记为负数,因此用算式表示就是:
②
合作探究
(2)如上图,由于小刚掉头向西走了3km,把原来向东走的1km抵消了,因此小刚两次行走的效果等于从点O向西走了(3﹣1)km.用算式表示就是:
③
合作探究
异号两数相加,当两数的绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值.
由②、③式受到启发,数学上规定:
②
③
合作探究
(1)
互为相反数的两个数相加,和为多少?
(2)
一个数与0相加,和为多少?
因为先从原点O向东走一段路程,又掉头走同样长的一段路程,最后结果回到了原点O处。所以互为相反数的两个数相加,和为0。
合作探究
互为相反数的两个数相加得0;
一个数与0相加仍得这个数.
于是,数学上规定:
合作探究
从上面有理数加法的规定可以得出:
如果两个数的和为0,那么这两个数互为相反数.
例题讲解
解:
(1)
(-5)+9=
(2)
7+(-10)=
例2
计算:
(1)
(-5)+9;
(2)
7+(-10);
(3)
;
(4)
.
+(9-5)
=4.
-(10-7)
=-3.
例题讲解
(4)
(3)
=0.
新知讲解
说一说有理数加法的计算方法。
1.
先根据有理数的加法法则确定结果的符号;
2.
再根据有理数的加法法则确定结果的绝对值。
巩固练习
1.
计算(-7)+(-9)的结果是
(
)
A.
-2
B.
2
C.
16
D.
-16
解析:根据两个负数相加,结果是负数,并且把绝对值相加,可知(-7)+(-9)=-(7+9)=-16。故选D.
D
巩固练习
2.
计算(-6)+15的结果是
(
)
A.
-9
B.
9
C.
21
D.
-21
解析:根据异号两数相加,当两数的绝对值不相等时,取绝对值较大的加数,并且用较大值减去较小的绝对值,可知(-6)+15=+(15-6)=9。故选B.
B
巩固练习
3.
下列说法中,错误的是
(
)
A.
两个负数的和为负数
B.
一个数与0相加,仍得这个数。
C.
互为相反数的两个数的和等于0
D.
一个正数加上一个负数的和是正数。
D
解析:根据有理数的加法法则,A,B,C正确。故选D.
巩固练习
4.
某地某天早上的气温是-2℃,到中午时气温上升了8℃,该地某天中午的气温是
(
)
A.
-10℃
B.
10℃
C.
-6℃
D.
6℃
D
解析:该地某天中午的气温是(-2)+8=+(8-2)=6℃
.故选D。
课堂总结
1.有理数的加法法则(规定)有哪些?
两个负数相加,结果是负数,并且把它们的绝对值相加.
绝对值不相等的异号两数相加取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得0;
一个数与0相加仍得这个数.
课堂总结
2.
如何运用有理数的加法法则进行运算?
一是确定符号:两个负数相加取负号,异号两数相加取绝对值较大的加数的符号;
二是计算绝对值:同号两数相加把绝对值相加,异号两数相加绝对值大的减去小的。
课堂总结
课后作业
1.
如图,在数轴上,点A,点B表示的数分别是a,b,则a+b的值是(
)
A.
正数
B.
负数
C.
0
D.
正数或负数
解析:从点A,点B在数轴上的位置可知,a为负数,b为正数,且|a|>|b|,根据异号两数相加的加法法则,a+b是负数,故选B.
B
课后作业
2.
计算:
(1)
(-11)+(-9);
(2)
(-7)+0;
(3)
8+(-20);
(4)
(-9)+9;
(5)
(-10)+7;
(6)
课后作业
3.
某地8∶00的气温是-5℃,根据天气预报15∶00的气温比8∶00的气温将上升了3~6℃,该地15∶00的气温不低于多少度?
解:该地15∶00的气温比8∶00的气温最低将上升3℃,因此15∶00的气温不低于(-5)+3=-2℃.
https://www.21cnjy.com/help/help_extract.php
1.4.1
有理数的加法(1)
湘教版
七年级上
教学目标
1.
理解、记住有理数的三条加法法则;
2.
能正确地根据有理数的加法法则进行运算;
3.
通过观察、计算,培养思维的灵活性,计算的严谨性.
新知导入
我们已经会计算两个非负数的和,即计算两个正数之和,0与正数之和,如8+12=20,3.75+0.25=4,0+2.3=2.3。
下面的加法算式与两个非负数的和有何不同?
(-4)+(﹣3)
(-4)+21
8+(-10)
0+(-7)
如何计算含有负数的有理数的加法呢?
新知讲解
如何计算两个负数的和?
探究:如图,在一条东西向的笔直马路上,任取一点O.若把向东走1km记为1,则向西走1km记为-1.
小丽从点O出发,先向西走2km,然后继续向西走3km,两次行走后,小丽从O点向哪个方向走了多少千米?
新知讲解
两次行走后,小丽从O点向西走了(2+3)km,因为向西走的路程记为负数,因此用算式表示就是
①
新知讲解
两个负数相加,结果是负数,并且把它们的绝对值相加.
由①式得到启发,数学上规定:
新知讲解
例1
计算:
(1)
(-8)+(-12);
(2)
(-3.75)+(-0.25).
解:(1)
(-8)+(-12)=
-(8+12)
=-20;
(2)
(-3.75)+(-0.25)
=-(3.75+0.25)
=-4.
合作探究
如何求一个正数与一个负数的和?
探究:在一条东西向的笔直马路上,任取一点O.若把向东走1km记为1,则向西走1km记为-1。
(1)小亮从O点出发,先向东走了4km,然后掉头向西走1km,小亮两次行走的效果等于从点O向哪个方向走了多少米?
(2)小刚从点O出发,先向东走了1km,然后掉头向西走3km,小刚两次行走的效果等于从点O向哪个方向走了多少米?
合作探究
(1)如图,由于向西走1km抵消了原来向东走4km中的1km,因此小亮两次行走的效果等于从点O向东走了(4-1)km.因为向东走的路程记为正数,向西走的路程记为负数,因此用算式表示就是:
②
合作探究
(2)如上图,由于小刚掉头向西走了3km,把原来向东走的1km抵消了,因此小刚两次行走的效果等于从点O向西走了(3﹣1)km.用算式表示就是:
③
合作探究
异号两数相加,当两数的绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值.
由②、③式受到启发,数学上规定:
②
③
合作探究
(1)
互为相反数的两个数相加,和为多少?
(2)
一个数与0相加,和为多少?
因为先从原点O向东走一段路程,又掉头走同样长的一段路程,最后结果回到了原点O处。所以互为相反数的两个数相加,和为0。
合作探究
互为相反数的两个数相加得0;
一个数与0相加仍得这个数.
于是,数学上规定:
合作探究
从上面有理数加法的规定可以得出:
如果两个数的和为0,那么这两个数互为相反数.
例题讲解
解:
(1)
(-5)+9=
(2)
7+(-10)=
例2
计算:
(1)
(-5)+9;
(2)
7+(-10);
(3)
;
(4)
.
+(9-5)
=4.
-(10-7)
=-3.
例题讲解
(4)
(3)
=0.
新知讲解
说一说有理数加法的计算方法。
1.
先根据有理数的加法法则确定结果的符号;
2.
再根据有理数的加法法则确定结果的绝对值。
巩固练习
1.
计算(-7)+(-9)的结果是
(
)
A.
-2
B.
2
C.
16
D.
-16
解析:根据两个负数相加,结果是负数,并且把绝对值相加,可知(-7)+(-9)=-(7+9)=-16。故选D.
D
巩固练习
2.
计算(-6)+15的结果是
(
)
A.
-9
B.
9
C.
21
D.
-21
解析:根据异号两数相加,当两数的绝对值不相等时,取绝对值较大的加数,并且用较大值减去较小的绝对值,可知(-6)+15=+(15-6)=9。故选B.
B
巩固练习
3.
下列说法中,错误的是
(
)
A.
两个负数的和为负数
B.
一个数与0相加,仍得这个数。
C.
互为相反数的两个数的和等于0
D.
一个正数加上一个负数的和是正数。
D
解析:根据有理数的加法法则,A,B,C正确。故选D.
巩固练习
4.
某地某天早上的气温是-2℃,到中午时气温上升了8℃,该地某天中午的气温是
(
)
A.
-10℃
B.
10℃
C.
-6℃
D.
6℃
D
解析:该地某天中午的气温是(-2)+8=+(8-2)=6℃
.故选D。
课堂总结
1.有理数的加法法则(规定)有哪些?
两个负数相加,结果是负数,并且把它们的绝对值相加.
绝对值不相等的异号两数相加取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得0;
一个数与0相加仍得这个数.
课堂总结
2.
如何运用有理数的加法法则进行运算?
一是确定符号:两个负数相加取负号,异号两数相加取绝对值较大的加数的符号;
二是计算绝对值:同号两数相加把绝对值相加,异号两数相加绝对值大的减去小的。
课堂总结
课后作业
1.
如图,在数轴上,点A,点B表示的数分别是a,b,则a+b的值是(
)
A.
正数
B.
负数
C.
0
D.
正数或负数
解析:从点A,点B在数轴上的位置可知,a为负数,b为正数,且|a|>|b|,根据异号两数相加的加法法则,a+b是负数,故选B.
B
课后作业
2.
计算:
(1)
(-11)+(-9);
(2)
(-7)+0;
(3)
8+(-20);
(4)
(-9)+9;
(5)
(-10)+7;
(6)
课后作业
3.
某地8∶00的气温是-5℃,根据天气预报15∶00的气温比8∶00的气温将上升了3~6℃,该地15∶00的气温不低于多少度?
解:该地15∶00的气温比8∶00的气温最低将上升3℃,因此15∶00的气温不低于(-5)+3=-2℃.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
