1.3.2函数的极值与导数-课件(含说课)-2020-2021学年高二下学期数学人教A版选修2-2第一章导数及其应用(共23张PPT)
文档属性
| 名称 | 1.3.2函数的极值与导数-课件(含说课)-2020-2021学年高二下学期数学人教A版选修2-2第一章导数及其应用(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 917.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
1.3.2
函数的极值与导数
庐山
题西林壁
苏轼[宋]
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
庐山
1,创设情景,引入课题
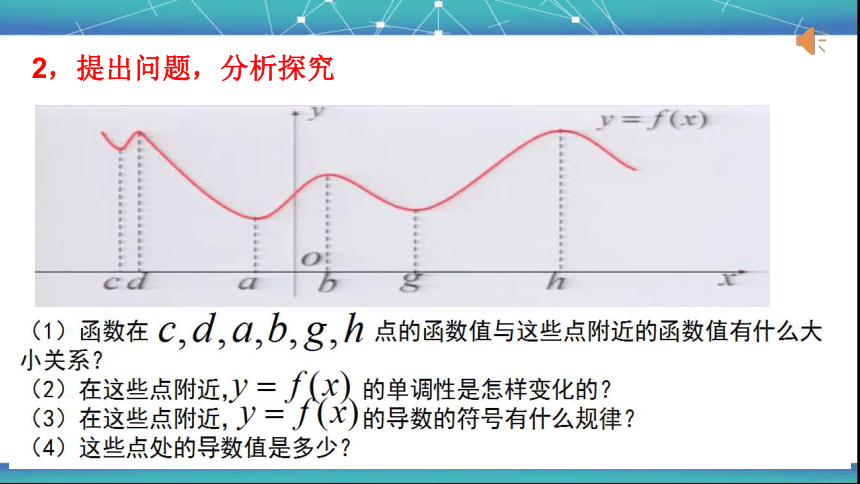
下图为庐山主峰的部分剖面图:
“横看成岭侧成峰,远近高低各不同”描述的是庐山的高低起伏错落有致,在群山中各个山峰的顶端虽然不一定是群山的最高处,但它却是附近的最高点,各个山谷的底端虽然不一定是群山的最底处,但它却是附近的最低点。那么其中到底蕴含了怎样的数学知识和数学思想呢?
2,提出问题,分析探究
(1)极小值点与极小值
如图,一般地,设函数y=f(x)及y=f'(x)在点x=a及其附近有定义,函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值_____,且______;而且在点x=a的左侧_________,右侧________,则把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
f′(x)<0
f′(x)>0
x
y
o
a
b
y=f(x)
<0
>0
f
’(a)=0
都小
f′(a)=0
3,抽象概括,形成概念
(2)极大值点与极大值
如图,一般地,设函数y=f(x)及y=f'(x)在点x=b及其附近有定义函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值____,且_______;而且在点x=b的左侧________,右侧________,则把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值._________、_________统称为极值点,_______和_______统称为极值.
f′(x)>0
f′(x)<0
极大值点
极小值点
极大值
极小值
<0
>0
x
y
o
a
b
y=f(x)
都大
f′(b)=0
f′(b)=0
y
a
b
x1
x2
x3
x4
O
x
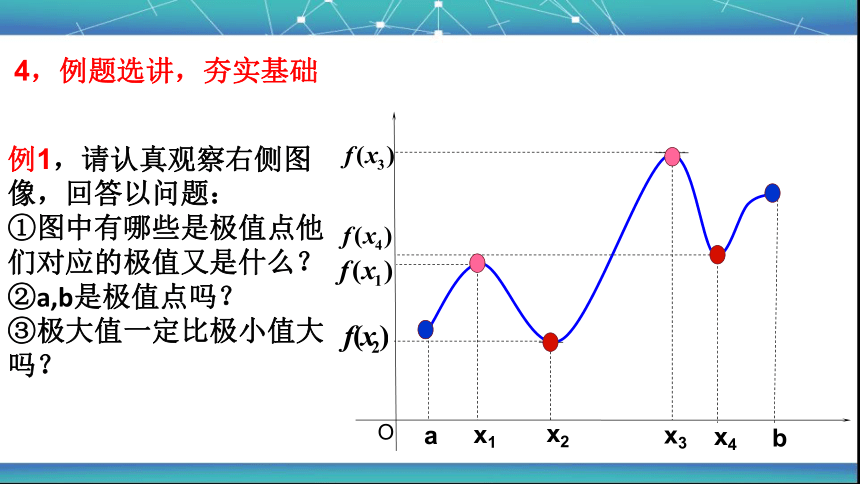
例1,请认真观察右侧图像,回答以问题:
①图中有哪些是极值点他们对应的极值又是什么?
②a,b是极值点吗?
③极大值一定比极小值大吗?
4,例题选讲,夯实基础
注意:
o
a
x1
x2
x3
x4
b
x
y
P(x1,f(x1))
y=f(x)
Q(x2,f(x2))
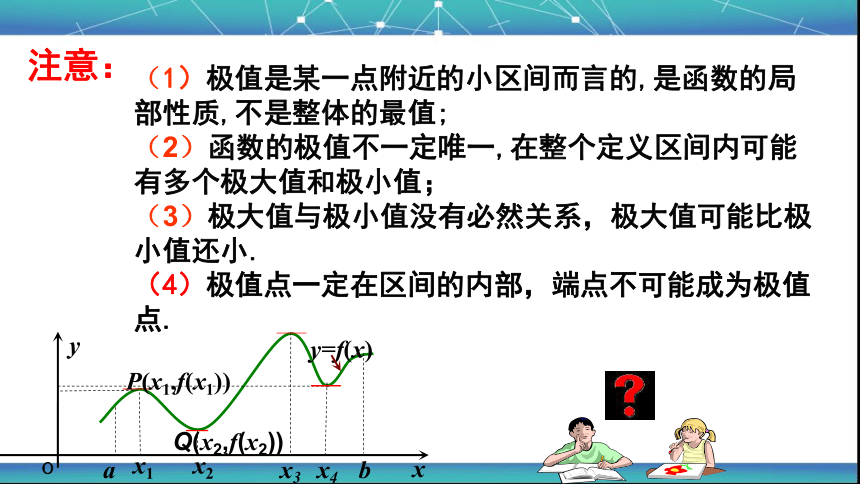
(1)极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2)函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
(3)极大值与极小值没有必然关系,极大值可能比极小值还小.
(4)极值点一定在区间的内部,端点不可能成为极值点.
解:f′(x)=3x2-6x-9.
解方程3x2-6x-9=0,得x1=-1,x2=3.
当x变化时,f′(x)与f(x)的变化情况如下表:
x
(-∞,-1)
-1
(-1,3)
3
(3,+∞)
f′(x)
+
0
-
0
+
f(x)
单调递增
10
单调递减
-22
单调递增
因此,当x=-1时函数取得极大值,且极大值为f(-1)=10;
当x=3时函数取得极小值,且极小值为f(3)=-22.
例2求函数
的极值.
求函数极值(极大值,极小值)的一般步骤:
(1)确定函数的定义域;
(2)求方程
的根;
(3)用方程
的根,顺次将函数的定义域分成若干个开区间,并列成表格;
(4)由
在方程
的根左右的符号,来判断
在这个根处取极值的情况.
若
左正右负,则
为极大值;
若
左负右正,则
为极小值.
求导
求极点
列表
求极值
定义域
求函数
的极值.
5,自主练习,展示成果
思考:导数为0的点一定是极值点吗?
6,循序渐进,突破难点
例题3:判断函数
有无极值?
结论:
若
是极值,则
;
反之,若
,则
不一定是极值.
即函数的导数等于零是函数在该点取得极值的必要不充分条件
7,回顾反思,总结提升:
1、极大值、极小值的定义;
2、利用导数求极值的方法.
数学素养:
知识层面:
数形结合思想;观察、归纳总结思想.
“不识庐山真面目,只缘身在此山中”讲的是为什么不能辨别庐山的真面目呢?只因为我们身在庐山之中,我们的视野被庐山的峰峦所局限,我们只能看到庐山的一峰一谷,一丘一壑,要想从整体把握庐山,我们必须走出庐山,全面考虑,那么,这其中又蕴含了怎样的数学知识呢?它其实就是我们下节课要讲的《函数的最值与导数》
作业:
必做题:教材P32业第五题
选做题:求函数
的极值
《函数的极值与导数》
说课稿
一、说教材
1、教材的地位和作用
本节课选自高中数学人教A版选修2-2教材1.3.2??函数的极值与导数,就本册教材而言本节既是前面所学导数的概念、导数的几何意义、导数的计算、函数的单调性与导数等内容的延续和深化,又为下节课最值的学习奠定了知识与方法的基础,起着承上启下的作用,就整个高中教学而言,函数是高中数学主要研究的内容之一,而导数又是研究函数的主要工具,同时导数在化学、物理中都有所涉及可见它的重要性。
2、教学目标
1、把握极大值、极小值的概念,会用导数求函数的极值;
2、理解解函数在某点取得极值的必要条件与充分条件;
3、培养学生观察、分析、探究、推理得出数学概念和规律的学习能力,能用数学的眼光看世界,从而培养数学素养;
3、教学重难点
重点:利用导数求函数的极值
难点:函数在某点取得极值的必要条件与充分条件
二、说教法学法
1、学情分析
基于本班学生基础较差,思维水平参差不齐,所以备课上既要考虑到薄弱同学的理解与接受,又要考虑到其他同学的视野拓展,因此在本节备课中我设置了许多问题,来引导学生怎样学,以问答的方式来激发学生的学习兴趣,同时让更多的学生参与到教学中来.学生已经学习了函数的单调性与导数的关系,已经初步具备了运用导数研究函数的能力,为了进一步培养学生的这种能力,体会导数的工具作用,本节进一步研究函数的极值与导数.
2、教法学法分析
在新课标的理念下,教师是学生学习的引导者、组织者、合作者和参与者.基于本节课的特点,我采用探究式和讲授式的教学方法.
在教师的引导下学生以自主探索、合作交流的方式进行学习.
体现数学逻辑推理的核心素养
三、教学过程
1.导入
2.讲述新课:极小值和极大值的定义
怎样导数求函数极值
函数在某点取得极值的必要条件与充分条件
3.练习
4.小结
5.布置作业
1.3.2
函数的极值与导数
庐山
题西林壁
苏轼[宋]
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
庐山
1,创设情景,引入课题
下图为庐山主峰的部分剖面图:
“横看成岭侧成峰,远近高低各不同”描述的是庐山的高低起伏错落有致,在群山中各个山峰的顶端虽然不一定是群山的最高处,但它却是附近的最高点,各个山谷的底端虽然不一定是群山的最底处,但它却是附近的最低点。那么其中到底蕴含了怎样的数学知识和数学思想呢?
2,提出问题,分析探究
(1)极小值点与极小值
如图,一般地,设函数y=f(x)及y=f'(x)在点x=a及其附近有定义,函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值_____,且______;而且在点x=a的左侧_________,右侧________,则把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.
f′(x)<0
f′(x)>0
x
y
o
a
b
y=f(x)
<0
>0
f
’(a)=0
都小
f′(a)=0
3,抽象概括,形成概念
(2)极大值点与极大值
如图,一般地,设函数y=f(x)及y=f'(x)在点x=b及其附近有定义函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值____,且_______;而且在点x=b的左侧________,右侧________,则把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值._________、_________统称为极值点,_______和_______统称为极值.
f′(x)>0
f′(x)<0
极大值点
极小值点
极大值
极小值
<0
>0
x
y
o
a
b
y=f(x)
都大
f′(b)=0
f′(b)=0
y
a
b
x1
x2
x3
x4
O
x
例1,请认真观察右侧图像,回答以问题:
①图中有哪些是极值点他们对应的极值又是什么?
②a,b是极值点吗?
③极大值一定比极小值大吗?
4,例题选讲,夯实基础
注意:
o
a
x1
x2
x3
x4
b
x
y
P(x1,f(x1))
y=f(x)
Q(x2,f(x2))
(1)极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2)函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
(3)极大值与极小值没有必然关系,极大值可能比极小值还小.
(4)极值点一定在区间的内部,端点不可能成为极值点.
解:f′(x)=3x2-6x-9.
解方程3x2-6x-9=0,得x1=-1,x2=3.
当x变化时,f′(x)与f(x)的变化情况如下表:
x
(-∞,-1)
-1
(-1,3)
3
(3,+∞)
f′(x)
+
0
-
0
+
f(x)
单调递增
10
单调递减
-22
单调递增
因此,当x=-1时函数取得极大值,且极大值为f(-1)=10;
当x=3时函数取得极小值,且极小值为f(3)=-22.
例2求函数
的极值.
求函数极值(极大值,极小值)的一般步骤:
(1)确定函数的定义域;
(2)求方程
的根;
(3)用方程
的根,顺次将函数的定义域分成若干个开区间,并列成表格;
(4)由
在方程
的根左右的符号,来判断
在这个根处取极值的情况.
若
左正右负,则
为极大值;
若
左负右正,则
为极小值.
求导
求极点
列表
求极值
定义域
求函数
的极值.
5,自主练习,展示成果
思考:导数为0的点一定是极值点吗?
6,循序渐进,突破难点
例题3:判断函数
有无极值?
结论:
若
是极值,则
;
反之,若
,则
不一定是极值.
即函数的导数等于零是函数在该点取得极值的必要不充分条件
7,回顾反思,总结提升:
1、极大值、极小值的定义;
2、利用导数求极值的方法.
数学素养:
知识层面:
数形结合思想;观察、归纳总结思想.
“不识庐山真面目,只缘身在此山中”讲的是为什么不能辨别庐山的真面目呢?只因为我们身在庐山之中,我们的视野被庐山的峰峦所局限,我们只能看到庐山的一峰一谷,一丘一壑,要想从整体把握庐山,我们必须走出庐山,全面考虑,那么,这其中又蕴含了怎样的数学知识呢?它其实就是我们下节课要讲的《函数的最值与导数》
作业:
必做题:教材P32业第五题
选做题:求函数
的极值
《函数的极值与导数》
说课稿
一、说教材
1、教材的地位和作用
本节课选自高中数学人教A版选修2-2教材1.3.2??函数的极值与导数,就本册教材而言本节既是前面所学导数的概念、导数的几何意义、导数的计算、函数的单调性与导数等内容的延续和深化,又为下节课最值的学习奠定了知识与方法的基础,起着承上启下的作用,就整个高中教学而言,函数是高中数学主要研究的内容之一,而导数又是研究函数的主要工具,同时导数在化学、物理中都有所涉及可见它的重要性。
2、教学目标
1、把握极大值、极小值的概念,会用导数求函数的极值;
2、理解解函数在某点取得极值的必要条件与充分条件;
3、培养学生观察、分析、探究、推理得出数学概念和规律的学习能力,能用数学的眼光看世界,从而培养数学素养;
3、教学重难点
重点:利用导数求函数的极值
难点:函数在某点取得极值的必要条件与充分条件
二、说教法学法
1、学情分析
基于本班学生基础较差,思维水平参差不齐,所以备课上既要考虑到薄弱同学的理解与接受,又要考虑到其他同学的视野拓展,因此在本节备课中我设置了许多问题,来引导学生怎样学,以问答的方式来激发学生的学习兴趣,同时让更多的学生参与到教学中来.学生已经学习了函数的单调性与导数的关系,已经初步具备了运用导数研究函数的能力,为了进一步培养学生的这种能力,体会导数的工具作用,本节进一步研究函数的极值与导数.
2、教法学法分析
在新课标的理念下,教师是学生学习的引导者、组织者、合作者和参与者.基于本节课的特点,我采用探究式和讲授式的教学方法.
在教师的引导下学生以自主探索、合作交流的方式进行学习.
体现数学逻辑推理的核心素养
三、教学过程
1.导入
2.讲述新课:极小值和极大值的定义
怎样导数求函数极值
函数在某点取得极值的必要条件与充分条件
3.练习
4.小结
5.布置作业
