1.3三角函数的诱导公式课件(含说课稿)-2021-2022学年高一上学期数学人教A版必修4(共21张PPT)
文档属性
| 名称 | 1.3三角函数的诱导公式课件(含说课稿)-2021-2022学年高一上学期数学人教A版必修4(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 292.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
1.3
三角函数的诱导公式
教学目标
(1)理解并掌握三角函数的诱导公式的推导过程、公式的特点,在此基础上,并能初步应用公式解决与之有关的问题。
(2)通过对公式推导方法的探索与发现,向学生渗透特殊到一般、类比与转化、化归等数学思想,培养学生观察、比较、抽象、概括等逻辑思维能力,培养逻辑推理的数学核心素养。
复习引入
1.三角函数的定义是什么?诱导公式一的作用是什么?
2.给出一个问题:求
探究:
给定一个角α.
1、角π+α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
3、角π-α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
2、角-α的的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
x
y
O
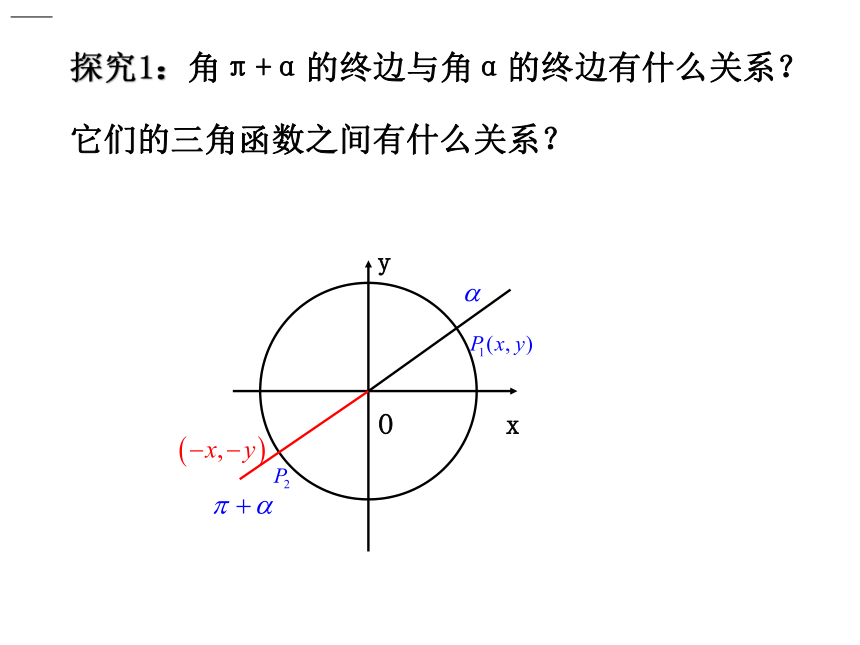
探究1:角π+α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
诱导公式(二)
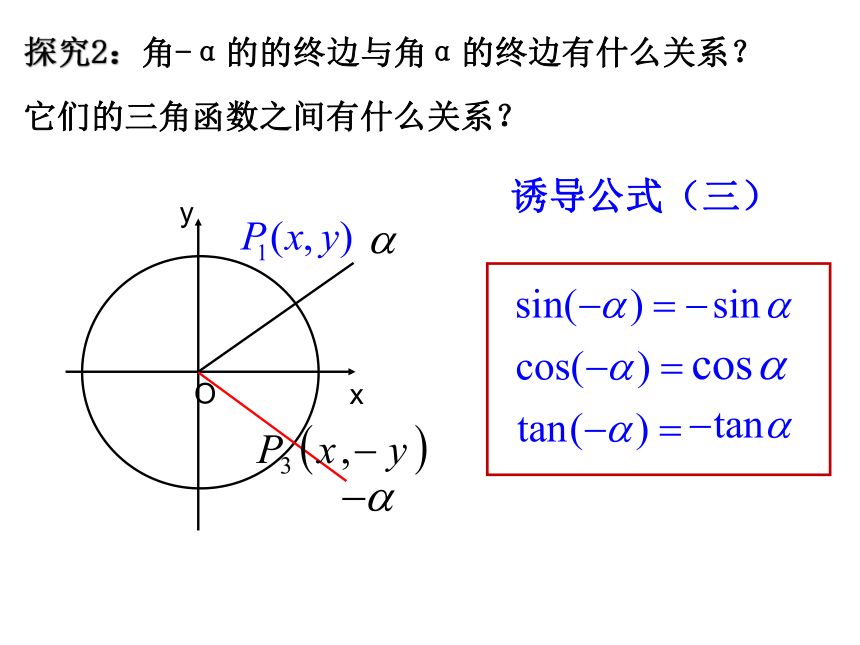
诱导公式(三)
x
y
O
探究2:角-α的的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
x
y
O
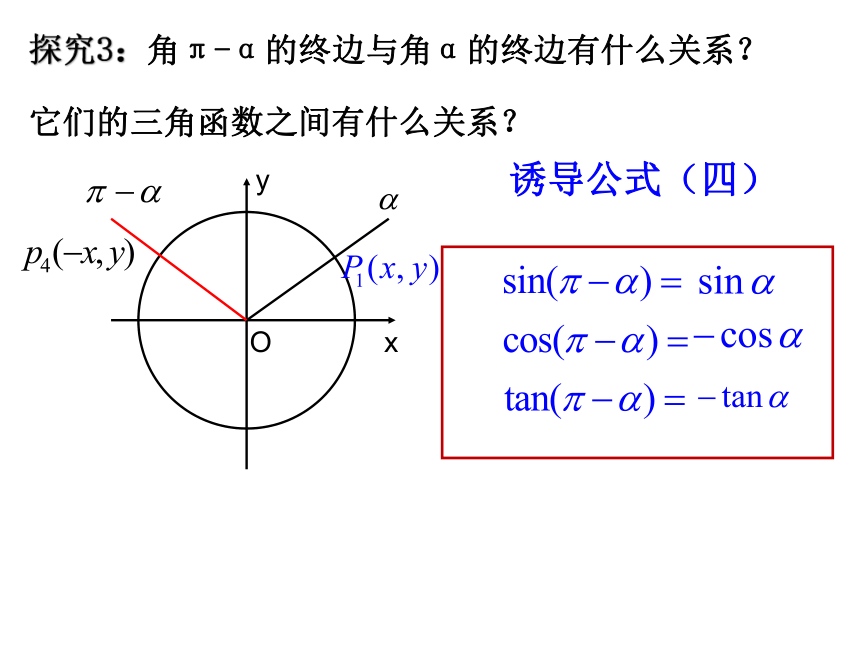
诱导公式(四)
探究3:角π-α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
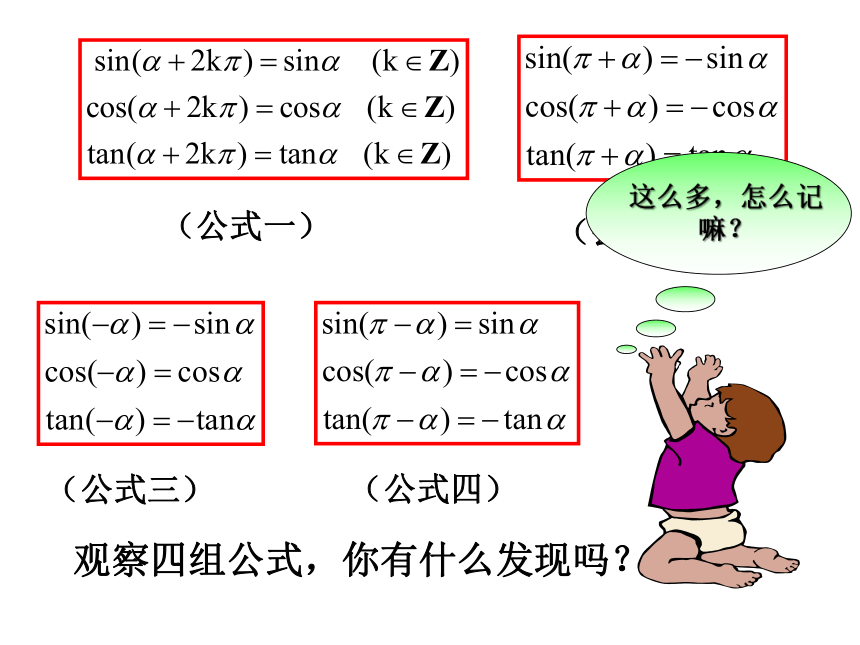
(公式一)
(公式二)
(公式三)
(公式四)
这么多,怎么记嘛?
观察四组公式,你有什么发现吗?
结论:对于刚才的发现,用一句话来概括
简记为“函数名不变,符号看象限”.
的三角函数值,等于α的同名三角函数值前面
加上把α看作锐角时原函数值的符号.
例1
解:
求下列各题的三角函数值是多少?
原式
3、例题讲解
任意负角的
三角函数
任意正角的
三角函数
的三
角函数
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
上述过程体现了由未知到已知的化归思想。
负化正,大化小,化到锐角为终了。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
练习:利用公式求下列三角函数值:
1.
诱导公式作用是什么?
2.
诱导公式怎样记呢?
转化口诀:大化小,负化正,,化到锐角就行了。
简记为“函数名不变,符号看象限”
课堂小结
《三角函数的诱导公式》
说课稿
一、说教材
1、教材的地位和作用
本节课是人教A版必修四第一章第三节第一课时的内容,是学生已学习过的三角函数定义、同角三角函数基本关系式及诱导公式(一)等知识的延续和拓展,为推导公式(五)、(六)提供方法指导,对以后解决三角函数化简,计算求值,证明三角函数恒等关系有着重要作用。
同时诱导公式的推导过程,体现了数学中数形结合和化归的思想方法,反映了从特殊到一般的数学归纳思维形式,这些都是学生今后学习和工作中必备的数学素养。这对培养学生的创新意识、发展学生的思维能力,掌握数学的思想方法具有重大的意义。
2、教学目标
(1)理解并掌握三角函数的诱导公式的推导过程、公式的特点,在此基础上,并能初步应用公式解决与之有关的问题。
(2)通过对公式推导方法的探索与发现,向学生渗透特殊到一般、类比与转化、化归等数学思想,培养学生观察、比较、抽象、概括等逻辑思维能力,从而培养逻辑推理的数学核心素养。
3、教学重难点
教学重点:诱导公式的推导及应用。
教学难点:相关角边的几何对称关系及诱导公式结构特征的认识。
二、说教法学法
1、学情分析
本课之前学生已经学习了三角函数的定义,对数形结合思想有了一定的了解,出现一定逻辑思维,但还有待提高,而且这一时期的学生思维比较活跃,创造性强,有了一点抽象思维,但还是需要感性的思维辅助。
2、教法学法分析
在新课标的理念下,教师是学生学习的引导者、组织者、合作者和参与者.基于本节课的特点,我采用探究式和讲授式的教学方法.
在教师的引导下学生以自主探索、合作交流的方式进行学习.在学习中了解和体验公式的生成过程,通过类比、归纳等思想推导公式.
体现数学逻辑推理的核心素养
三、教学过程
1.导入
2.讲述新课:公式(二、三、四)
公式的记忆
3.练习
4.小结
5.布置作业
1.3
三角函数的诱导公式
教学目标
(1)理解并掌握三角函数的诱导公式的推导过程、公式的特点,在此基础上,并能初步应用公式解决与之有关的问题。
(2)通过对公式推导方法的探索与发现,向学生渗透特殊到一般、类比与转化、化归等数学思想,培养学生观察、比较、抽象、概括等逻辑思维能力,培养逻辑推理的数学核心素养。
复习引入
1.三角函数的定义是什么?诱导公式一的作用是什么?
2.给出一个问题:求
探究:
给定一个角α.
1、角π+α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
3、角π-α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
2、角-α的的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
x
y
O
探究1:角π+α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
诱导公式(二)
诱导公式(三)
x
y
O
探究2:角-α的的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
x
y
O
诱导公式(四)
探究3:角π-α的终边与角α的终边有什么关系?
它们的三角函数之间有什么关系?
(公式一)
(公式二)
(公式三)
(公式四)
这么多,怎么记嘛?
观察四组公式,你有什么发现吗?
结论:对于刚才的发现,用一句话来概括
简记为“函数名不变,符号看象限”.
的三角函数值,等于α的同名三角函数值前面
加上把α看作锐角时原函数值的符号.
例1
解:
求下列各题的三角函数值是多少?
原式
3、例题讲解
任意负角的
三角函数
任意正角的
三角函数
的三
角函数
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
上述过程体现了由未知到已知的化归思想。
负化正,大化小,化到锐角为终了。
通过例题,你能说说诱导公式的作用以及化任意角的三角函数为锐角三角函数的一般思路吗?
练习:利用公式求下列三角函数值:
1.
诱导公式作用是什么?
2.
诱导公式怎样记呢?
转化口诀:大化小,负化正,,化到锐角就行了。
简记为“函数名不变,符号看象限”
课堂小结
《三角函数的诱导公式》
说课稿
一、说教材
1、教材的地位和作用
本节课是人教A版必修四第一章第三节第一课时的内容,是学生已学习过的三角函数定义、同角三角函数基本关系式及诱导公式(一)等知识的延续和拓展,为推导公式(五)、(六)提供方法指导,对以后解决三角函数化简,计算求值,证明三角函数恒等关系有着重要作用。
同时诱导公式的推导过程,体现了数学中数形结合和化归的思想方法,反映了从特殊到一般的数学归纳思维形式,这些都是学生今后学习和工作中必备的数学素养。这对培养学生的创新意识、发展学生的思维能力,掌握数学的思想方法具有重大的意义。
2、教学目标
(1)理解并掌握三角函数的诱导公式的推导过程、公式的特点,在此基础上,并能初步应用公式解决与之有关的问题。
(2)通过对公式推导方法的探索与发现,向学生渗透特殊到一般、类比与转化、化归等数学思想,培养学生观察、比较、抽象、概括等逻辑思维能力,从而培养逻辑推理的数学核心素养。
3、教学重难点
教学重点:诱导公式的推导及应用。
教学难点:相关角边的几何对称关系及诱导公式结构特征的认识。
二、说教法学法
1、学情分析
本课之前学生已经学习了三角函数的定义,对数形结合思想有了一定的了解,出现一定逻辑思维,但还有待提高,而且这一时期的学生思维比较活跃,创造性强,有了一点抽象思维,但还是需要感性的思维辅助。
2、教法学法分析
在新课标的理念下,教师是学生学习的引导者、组织者、合作者和参与者.基于本节课的特点,我采用探究式和讲授式的教学方法.
在教师的引导下学生以自主探索、合作交流的方式进行学习.在学习中了解和体验公式的生成过程,通过类比、归纳等思想推导公式.
体现数学逻辑推理的核心素养
三、教学过程
1.导入
2.讲述新课:公式(二、三、四)
公式的记忆
3.练习
4.小结
5.布置作业
