第23章 数据分析单元测试卷(Word版 含答案) 2021-2022学年冀教版数学九年级上册
文档属性
| 名称 | 第23章 数据分析单元测试卷(Word版 含答案) 2021-2022学年冀教版数学九年级上册 |  | |
| 格式 | doc | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 09:12:40 | ||
图片预览




文档简介
2021-2022学年冀教新版九年级上册数学《第23章
数据分析》单元测试卷
一.选择题
1.为了了解全校七年级300名学生的视力情况,骆老师从中抽查了50名学生的视力情况.针对这个问题,下面说法正确的是( )
A.300名学生是总体
B.每名学生是个体
C.50名学生是所抽取的一个样本
D.这个样本容量是50
2.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15
B.14.16
C.14.17
D.14.20
3.已知5个正数a1,a2,a3,a4,a5的平均数是a,且a1>a2>a3>a4>a5,则数据a1,a2,a3,0,a4,a5的平均数和中位数是( )
A.a,
B.a,
C.
a,
D.
a,
4.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
180
185
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁
5.数据﹣1,0,3,4,4的平均数是( )
A.4
B.3
C.2.5
D.2
6.数据1,2,3,4,5,﹣3的平均数是( )
A.2
B.3
C.4
D.5
7.某电子科技公司招聘本科毕业生,小林同学的心理测试、笔试、面试得分分别为80分、90分、70分.若依次按照2:3:5的比例确定成绩,则小林同学的最终成绩为( )
A.80分
B.85分
C.78分
D.82分
8.某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
劳动时间(小时)
3
3.5
4
4.5
人数
1
1
2
1
A.中位数是4,平均数是3.75
B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8
D.众数是2,平均数是3.8
9.甲,乙,丙,丁四位同学本学期5次50米短跑成绩的平均数(秒)及方差S2如下表所示.若从这四位同学中选出一位成绩较好且状态稳定的同学参加学校比赛,则应该选的同学是( )
甲
乙
丙
丁
7
7
7.5
7.5
s2
0.45
0.2
0.2
0.45
A.甲
B.乙
C.丙
D.丁
10.某班在统计全班33人的体重时,算出中位数与平均数都是54千克,但后来发现在计算时,将其中一名学生的体重50千克错写成了5千克,经重新计算后,正确的中位数为a千克,正确的平均数为b千克,那么( )
A.a<b
B.a=b
C.a>b
D.无法判断
二.填空题
11.某校八年级同学2020年4月平均每天自主学习时间统计如图所示,则这组数据的众数是
.
12.已知一组数据3,4,6,x,9的平均数是6,那么这组数据的方差等于
.
13.在某公司的面试中,李明的得分情况为:个人形象85分,工作能力90分,交际能力80分,已知个人形象、工作能力和交际能力的权重为1:2:2,则李明的最终成绩是
.
14.在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数是
.
15.若一组数据1,3,x,5,4,6的平均数是4,则这组数据的中位数是
.
16.为了了解我市6000名学生参加初中毕业会考数学考试的成绩情况,从中抽取了200名考生的成绩进行统计,在这个问题中,样本容量是
.
17.已知一组数据x1,x2,x3,x4的平均数是3,则数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2的平均数是
.
18.如果数据a,b,c的平均数是4,那么数据a+1,b+1,c+1的平均数是
.
19.在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差为1.2,乙的成绩的方差为3.9,由此可知
的成绩更稳定.
20.小颖使用计算器求30个数据的平均数时,错将其中一个数据15输入为105,那么由此求出的平均数与实际平均数的差是
.
三.解答题
21.在6.26国际禁毒日到来之际,重庆市教委为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛,某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
89
97
100
99
94
79
99
98
79
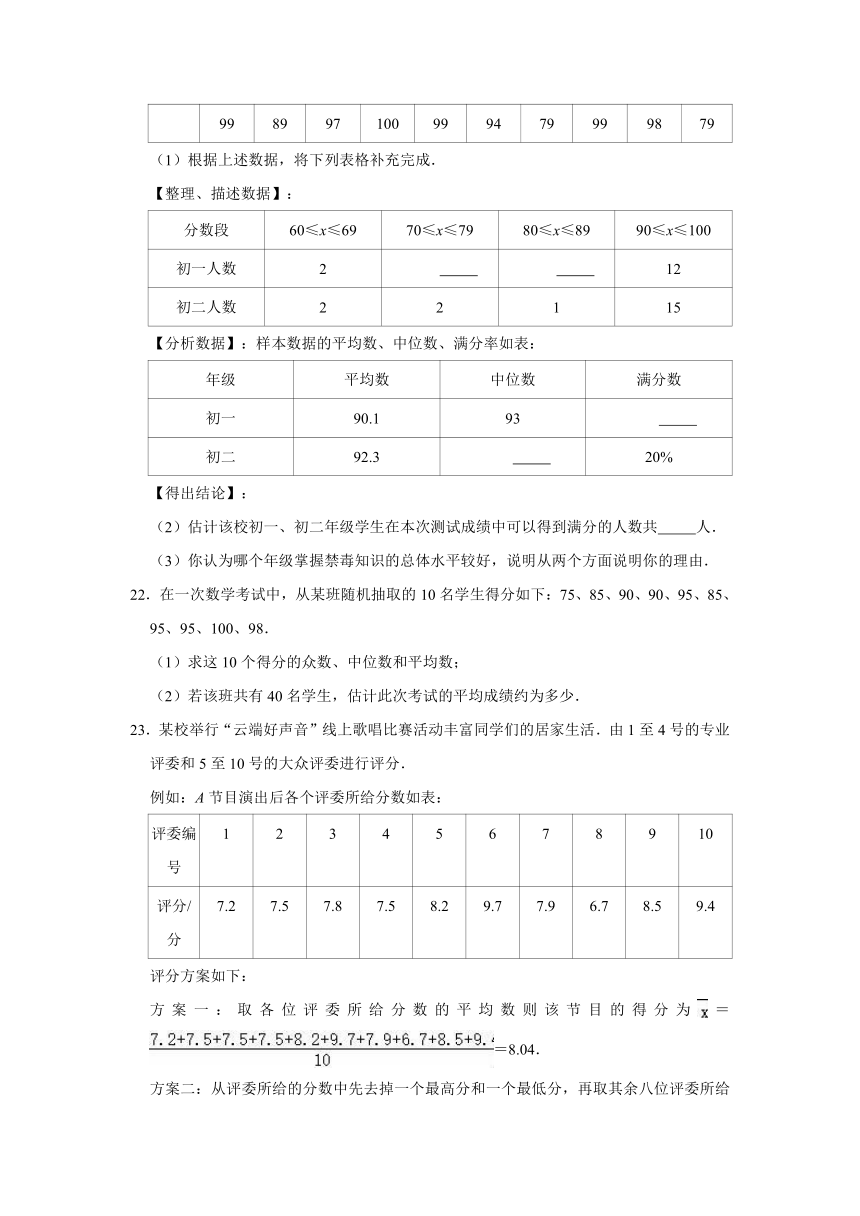
(1)根据上述数据,将下列表格补充完成.
【整理、描述数据】:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
12
初二人数
2
2
1
15
【分析数据】:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分数
初一
90.1
93
初二
92.3
20%
【得出结论】:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共
人.
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明从两个方面说明你的理由.
22.在一次数学考试中,从某班随机抽取的10名学生得分如下:75、85、90、90、95、85、95、95、100、98.
(1)求这10个得分的众数、中位数和平均数;
(2)若该班共有40名学生,估计此次考试的平均成绩约为多少.
23.某校举行“云端好声音”线上歌唱比赛活动丰富同学们的居家生活.由1至4号的专业评委和5至10号的大众评委进行评分.
例如:A节目演出后各个评委所给分数如表:
评委编号
1
2
3
4
5
6
7
8
9
10
评分/分
7.2
7.5
7.8
7.5
8.2
9.7
7.9
6.7
8.5
9.4
评分方案如下:
方案一:取各位评委所给分数的平均数则该节目的得分为==8.04.
方案二:从评委所给的分数中先去掉一个最高分和一个最低分,再取其余八位评委所给分数的平均数,则该节目的得分为==8.00.
回答下列问题:
(1)小乐认为“方案二”比“方案一”更合理,你
小乐的说法吗(填“同意”或“不同意”)?理由是
;
(2)小乐认为评分既要突出专业评审的权威性又要尊重大众评审的喜爱度,因此设计了“方案三”:先计算1至4号评委所给分数的平均数=7.5,5至10号评委所给分数的平均数=8.4,再根据比赛的需求设置相应的权重(f1表示专业评委的权重,f2表示大众评委的权重,且f1+f2=1).
如当f1=0.7时,则f2=1﹣0.7=0.3.
该节目的得分为=f1+f2=0.7×7.5+0.3×8.4=7.77.
Ⅰ.当按照“方案三”中f1=0.6评分时,A节目的得分为
.
Ⅱ.关于评分方案,下列说法正确的有
.
①当f1=0.5时,A节目按照“方案三”和“方案一”评分结果相同;
②当f1>0.4时,说明“方案三”评分更注重节目的专业性;
③当f1=0.3时,A节目按照“方案三”评分的结果比“方案一”和“方案二”都高.
24.某单位共有280位员工参加了社会公益捐款活动,从中任意抽取了12位员工的捐款数额,记录如表:
捐款数额/元
30
50
80
100
员工人数
2
5
3
2
估计该单位的捐款总额.
25.请指出下列抽样调查的总体、个体、样本、样本容量分别是什么?
(1)为了了解某种家用空调工作1小时的用电量,调查10台该种空调每台工作1小时的用电量;
(2)为了了解初二年级270名学生的视力情况,从中抽取50名学生进行视力检查.
26.下表是某班5名同学某次数学测试成绩.根据信息完成下表,并回答问题.五人中分数最高的是谁?分数最低的是谁?谁的分数与全班平均分最接近?
姓名
王芳
刘兵
张昕
李聪
江文
成绩
89
84
与全班平均分之差
﹣1
+2
0
﹣2
参考答案与试题解析
一.选择题
1.解:A、300名学生的视力情况是总体,故此选项错误;
B、每个学生的视力情况是个体,故此选项错误;
C、50名学生的视力情况是抽取的一个样本,故此选项错误;
D、这组数据的样本容量是50,故此选项正确.
故选:D.
2.解:借助计算器,先按MOOE按2再按1,会出现一竖,然后把你要求平均数的数字输进去,好了之后按AC键,再按shift再按1,然后按5,就会出现平均数的数值.
故选:B.
3.解:由平均数定义可知:(a1+a2+a3+0+a4+a5)=×5a=a;
将这组数据按从小到大排列为0,a5,a4,a3,a2,a1;由于有偶数个数,取最中间两个数的平均数.
∴其中位数为.
故选:C.
4.解:∵=>=,
∴从乙和丙中选择一人参加比赛,
∵S乙2<S丙2,
∴选择乙参赛,
故选:B.
5.解:==2,
故选:D.
6.解:=2,
故选:A.
7.解:小林同学的最终成绩为=78(分),
故选:C.
8.解:这组数据中4出现的次数最多,众数为4,
∵共有5个人,
∴第3个人的劳动时间为中位数,
故中位数为:4,
平均数为:=3.8.
故选:C.
9.解:∵乙的平均分最好,方差最小,最稳定,
∴应选乙.
故选:B.
10.解:原数据中5在中位数54的左边,新数据中50<54,
所以中位数a=54,
新数据比原数据增加了45,而数据的个数没有变化,
所以平均数b>54,
则b>a,
故选:A.
二.填空题
11.解:由条形图知,数据6出现次数最多,有52次,
∴这组数据的众数为6,
故答案为:6.
12.解:∵数据3,4,6,x,9的平均数是6,
∴(3+4+6+x+9)=6,
解得:x=8,
s2=
[(3﹣6)2+(4﹣6)2+(6﹣6)2+(8﹣6)2+(9﹣6)2]=5.2,
故答案为:5.2.
13.解:根据题意得:
=85,
故答案为:85分.
14.解:共有25个数,最中间的数为第13数,是96,所以数据的中位数为96分.
故答案为:96.
15.解:×(1+3+x+5+4+6)=4,
x=5,
将这组数据按小到大排列:1,3,4,5,5,6,
故中位数=4.5,
故答案为4.5.
16.解:样本容量是200.
故答案为:200.
17.解:一组数据x1,x2,x3,x4的平均数是3,有(x1+x2+x3+x4)=3,
那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数是(3x1﹣2+3x2﹣2+3x3﹣2+3x4﹣2+3x5﹣2)
=3×(x1+x2+x3+x4)﹣×(2+2+2+2)
=3×3﹣2
=7.
故答案为7.
18.解:∵a,b,c的平均数是4,
∴a+b+c=3×4=12,
则数据a+1,b+1,c+1的平均数是==5,
故答案为:5.
19.解:因为S甲2=1.2<S乙2=3.9,方差小的为甲,所以本题中成绩比较稳定的是甲.
故答案为:甲;
20.解:由题意知,错将其中一个数据15输入为105,则多加了105﹣15=90,所以平均数多了90÷30=3.
故填3.
三.解答题
21.解:(1)根据题意,得:初一人数:70≤x≤79的有2人,
80≤x≤89的有4人,
初一满分数:5÷20=25%,
初二中位数:(97+98)÷2=97.5,
故答案为:2,4,25%,97.5;
(2)初一满分的人数约为:300×25%=75(人),
初二满分的人数约为:300×20%=60(人),
∴共有75+60=135(人),
故答案为:135;
(3)初二学生掌握禁毒知识的水平比较好.
从平均分来看,初二的学生掌握禁毒知识的水平比较好;
从中位数来看,初二的学生掌握禁毒知识的水平比较好.
22.解:(1)数据由小到大排列为:75、85、85、90、90、95、95、95、98、100,
所以这10个得分的众数为95,中位数为=92.5,平均数=(75+85+85+90+90+95+95+95+98+100)=90.8;
(2)估计此次考试的平均成绩约为90.8分.
23.解:(1)同意,理由:平均数易受极端值影响,故方案二更合理;
故答案为:同意,平均数易受极端值影响,故方案二更合理;
(2)Ⅰ.当f1=0.6时,由题意知,f2=1﹣f1=0.4,=7.5,=8.4,
∴该节目得分:=f1+f2=0.6×7.5+0.4×8.4=7.86
∴f1=0.6时,A节目的得分为7.86.
故答案为:7.86;
Ⅱ.正确的有③.
①f1=0.5时,=f1+(1﹣f1)=0.5×7.5+0.5×8.4=7.95,
8.04≠7.95,故①错误;
②f1>0.4时,说明方案三评的更注重节目的专业性,故②正确;
③f1=0.3,=0.3×7.5+0.7×8.4=8.13,
∵8.13>8.04,8.13>8.00,
∴③正确.
故答案为:②③.
24.解:这12位员工的捐款数额平均数为,
以作为所有员工捐款的平均数,由此估计该单位的捐款总额约为280×62.5=17500(元).
25.解:(1)总体:该种家用空调工作1小时的用电量;个体:每一台该种家用空调工作1小时的用电量;样本:10台该种家用空调每台工作1小时的用电量;样本容量:10;
(2)总体:初二年级270名学生的视力情况;个体:每一名学生的视力情况;样本:抽取的50名学生的视力情况;样本容量:50.
26.解:完成表格得
姓名
王芳
刘兵
张昕
李聪
江文
成绩
89
92
90
84
88
与全班平均分之差
﹣1
+2
0
﹣6
﹣2
故答案为分数最高的是刘兵,分数最低的是李聪,张昕的分数与全班平均分最接近.
数据分析》单元测试卷
一.选择题
1.为了了解全校七年级300名学生的视力情况,骆老师从中抽查了50名学生的视力情况.针对这个问题,下面说法正确的是( )
A.300名学生是总体
B.每名学生是个体
C.50名学生是所抽取的一个样本
D.这个样本容量是50
2.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15
B.14.16
C.14.17
D.14.20
3.已知5个正数a1,a2,a3,a4,a5的平均数是a,且a1>a2>a3>a4>a5,则数据a1,a2,a3,0,a4,a5的平均数和中位数是( )
A.a,
B.a,
C.
a,
D.
a,
4.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
180
185
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁
5.数据﹣1,0,3,4,4的平均数是( )
A.4
B.3
C.2.5
D.2
6.数据1,2,3,4,5,﹣3的平均数是( )
A.2
B.3
C.4
D.5
7.某电子科技公司招聘本科毕业生,小林同学的心理测试、笔试、面试得分分别为80分、90分、70分.若依次按照2:3:5的比例确定成绩,则小林同学的最终成绩为( )
A.80分
B.85分
C.78分
D.82分
8.某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
劳动时间(小时)
3
3.5
4
4.5
人数
1
1
2
1
A.中位数是4,平均数是3.75
B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8
D.众数是2,平均数是3.8
9.甲,乙,丙,丁四位同学本学期5次50米短跑成绩的平均数(秒)及方差S2如下表所示.若从这四位同学中选出一位成绩较好且状态稳定的同学参加学校比赛,则应该选的同学是( )
甲
乙
丙
丁
7
7
7.5
7.5
s2
0.45
0.2
0.2
0.45
A.甲
B.乙
C.丙
D.丁
10.某班在统计全班33人的体重时,算出中位数与平均数都是54千克,但后来发现在计算时,将其中一名学生的体重50千克错写成了5千克,经重新计算后,正确的中位数为a千克,正确的平均数为b千克,那么( )
A.a<b
B.a=b
C.a>b
D.无法判断
二.填空题
11.某校八年级同学2020年4月平均每天自主学习时间统计如图所示,则这组数据的众数是
.
12.已知一组数据3,4,6,x,9的平均数是6,那么这组数据的方差等于
.
13.在某公司的面试中,李明的得分情况为:个人形象85分,工作能力90分,交际能力80分,已知个人形象、工作能力和交际能力的权重为1:2:2,则李明的最终成绩是
.
14.在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数是
.
15.若一组数据1,3,x,5,4,6的平均数是4,则这组数据的中位数是
.
16.为了了解我市6000名学生参加初中毕业会考数学考试的成绩情况,从中抽取了200名考生的成绩进行统计,在这个问题中,样本容量是
.
17.已知一组数据x1,x2,x3,x4的平均数是3,则数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2的平均数是
.
18.如果数据a,b,c的平均数是4,那么数据a+1,b+1,c+1的平均数是
.
19.在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差为1.2,乙的成绩的方差为3.9,由此可知
的成绩更稳定.
20.小颖使用计算器求30个数据的平均数时,错将其中一个数据15输入为105,那么由此求出的平均数与实际平均数的差是
.
三.解答题
21.在6.26国际禁毒日到来之际,重庆市教委为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛,某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
89
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完成.
【整理、描述数据】:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
12
初二人数
2
2
1
15
【分析数据】:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分数
初一
90.1
93
初二
92.3
20%
【得出结论】:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共
人.
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明从两个方面说明你的理由.
22.在一次数学考试中,从某班随机抽取的10名学生得分如下:75、85、90、90、95、85、95、95、100、98.
(1)求这10个得分的众数、中位数和平均数;
(2)若该班共有40名学生,估计此次考试的平均成绩约为多少.
23.某校举行“云端好声音”线上歌唱比赛活动丰富同学们的居家生活.由1至4号的专业评委和5至10号的大众评委进行评分.
例如:A节目演出后各个评委所给分数如表:
评委编号
1
2
3
4
5
6
7
8
9
10
评分/分
7.2
7.5
7.8
7.5
8.2
9.7
7.9
6.7
8.5
9.4
评分方案如下:
方案一:取各位评委所给分数的平均数则该节目的得分为==8.04.
方案二:从评委所给的分数中先去掉一个最高分和一个最低分,再取其余八位评委所给分数的平均数,则该节目的得分为==8.00.
回答下列问题:
(1)小乐认为“方案二”比“方案一”更合理,你
小乐的说法吗(填“同意”或“不同意”)?理由是
;
(2)小乐认为评分既要突出专业评审的权威性又要尊重大众评审的喜爱度,因此设计了“方案三”:先计算1至4号评委所给分数的平均数=7.5,5至10号评委所给分数的平均数=8.4,再根据比赛的需求设置相应的权重(f1表示专业评委的权重,f2表示大众评委的权重,且f1+f2=1).
如当f1=0.7时,则f2=1﹣0.7=0.3.
该节目的得分为=f1+f2=0.7×7.5+0.3×8.4=7.77.
Ⅰ.当按照“方案三”中f1=0.6评分时,A节目的得分为
.
Ⅱ.关于评分方案,下列说法正确的有
.
①当f1=0.5时,A节目按照“方案三”和“方案一”评分结果相同;
②当f1>0.4时,说明“方案三”评分更注重节目的专业性;
③当f1=0.3时,A节目按照“方案三”评分的结果比“方案一”和“方案二”都高.
24.某单位共有280位员工参加了社会公益捐款活动,从中任意抽取了12位员工的捐款数额,记录如表:
捐款数额/元
30
50
80
100
员工人数
2
5
3
2
估计该单位的捐款总额.
25.请指出下列抽样调查的总体、个体、样本、样本容量分别是什么?
(1)为了了解某种家用空调工作1小时的用电量,调查10台该种空调每台工作1小时的用电量;
(2)为了了解初二年级270名学生的视力情况,从中抽取50名学生进行视力检查.
26.下表是某班5名同学某次数学测试成绩.根据信息完成下表,并回答问题.五人中分数最高的是谁?分数最低的是谁?谁的分数与全班平均分最接近?
姓名
王芳
刘兵
张昕
李聪
江文
成绩
89
84
与全班平均分之差
﹣1
+2
0
﹣2
参考答案与试题解析
一.选择题
1.解:A、300名学生的视力情况是总体,故此选项错误;
B、每个学生的视力情况是个体,故此选项错误;
C、50名学生的视力情况是抽取的一个样本,故此选项错误;
D、这组数据的样本容量是50,故此选项正确.
故选:D.
2.解:借助计算器,先按MOOE按2再按1,会出现一竖,然后把你要求平均数的数字输进去,好了之后按AC键,再按shift再按1,然后按5,就会出现平均数的数值.
故选:B.
3.解:由平均数定义可知:(a1+a2+a3+0+a4+a5)=×5a=a;
将这组数据按从小到大排列为0,a5,a4,a3,a2,a1;由于有偶数个数,取最中间两个数的平均数.
∴其中位数为.
故选:C.
4.解:∵=>=,
∴从乙和丙中选择一人参加比赛,
∵S乙2<S丙2,
∴选择乙参赛,
故选:B.
5.解:==2,
故选:D.
6.解:=2,
故选:A.
7.解:小林同学的最终成绩为=78(分),
故选:C.
8.解:这组数据中4出现的次数最多,众数为4,
∵共有5个人,
∴第3个人的劳动时间为中位数,
故中位数为:4,
平均数为:=3.8.
故选:C.
9.解:∵乙的平均分最好,方差最小,最稳定,
∴应选乙.
故选:B.
10.解:原数据中5在中位数54的左边,新数据中50<54,
所以中位数a=54,
新数据比原数据增加了45,而数据的个数没有变化,
所以平均数b>54,
则b>a,
故选:A.
二.填空题
11.解:由条形图知,数据6出现次数最多,有52次,
∴这组数据的众数为6,
故答案为:6.
12.解:∵数据3,4,6,x,9的平均数是6,
∴(3+4+6+x+9)=6,
解得:x=8,
s2=
[(3﹣6)2+(4﹣6)2+(6﹣6)2+(8﹣6)2+(9﹣6)2]=5.2,
故答案为:5.2.
13.解:根据题意得:
=85,
故答案为:85分.
14.解:共有25个数,最中间的数为第13数,是96,所以数据的中位数为96分.
故答案为:96.
15.解:×(1+3+x+5+4+6)=4,
x=5,
将这组数据按小到大排列:1,3,4,5,5,6,
故中位数=4.5,
故答案为4.5.
16.解:样本容量是200.
故答案为:200.
17.解:一组数据x1,x2,x3,x4的平均数是3,有(x1+x2+x3+x4)=3,
那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数是(3x1﹣2+3x2﹣2+3x3﹣2+3x4﹣2+3x5﹣2)
=3×(x1+x2+x3+x4)﹣×(2+2+2+2)
=3×3﹣2
=7.
故答案为7.
18.解:∵a,b,c的平均数是4,
∴a+b+c=3×4=12,
则数据a+1,b+1,c+1的平均数是==5,
故答案为:5.
19.解:因为S甲2=1.2<S乙2=3.9,方差小的为甲,所以本题中成绩比较稳定的是甲.
故答案为:甲;
20.解:由题意知,错将其中一个数据15输入为105,则多加了105﹣15=90,所以平均数多了90÷30=3.
故填3.
三.解答题
21.解:(1)根据题意,得:初一人数:70≤x≤79的有2人,
80≤x≤89的有4人,
初一满分数:5÷20=25%,
初二中位数:(97+98)÷2=97.5,
故答案为:2,4,25%,97.5;
(2)初一满分的人数约为:300×25%=75(人),
初二满分的人数约为:300×20%=60(人),
∴共有75+60=135(人),
故答案为:135;
(3)初二学生掌握禁毒知识的水平比较好.
从平均分来看,初二的学生掌握禁毒知识的水平比较好;
从中位数来看,初二的学生掌握禁毒知识的水平比较好.
22.解:(1)数据由小到大排列为:75、85、85、90、90、95、95、95、98、100,
所以这10个得分的众数为95,中位数为=92.5,平均数=(75+85+85+90+90+95+95+95+98+100)=90.8;
(2)估计此次考试的平均成绩约为90.8分.
23.解:(1)同意,理由:平均数易受极端值影响,故方案二更合理;
故答案为:同意,平均数易受极端值影响,故方案二更合理;
(2)Ⅰ.当f1=0.6时,由题意知,f2=1﹣f1=0.4,=7.5,=8.4,
∴该节目得分:=f1+f2=0.6×7.5+0.4×8.4=7.86
∴f1=0.6时,A节目的得分为7.86.
故答案为:7.86;
Ⅱ.正确的有③.
①f1=0.5时,=f1+(1﹣f1)=0.5×7.5+0.5×8.4=7.95,
8.04≠7.95,故①错误;
②f1>0.4时,说明方案三评的更注重节目的专业性,故②正确;
③f1=0.3,=0.3×7.5+0.7×8.4=8.13,
∵8.13>8.04,8.13>8.00,
∴③正确.
故答案为:②③.
24.解:这12位员工的捐款数额平均数为,
以作为所有员工捐款的平均数,由此估计该单位的捐款总额约为280×62.5=17500(元).
25.解:(1)总体:该种家用空调工作1小时的用电量;个体:每一台该种家用空调工作1小时的用电量;样本:10台该种家用空调每台工作1小时的用电量;样本容量:10;
(2)总体:初二年级270名学生的视力情况;个体:每一名学生的视力情况;样本:抽取的50名学生的视力情况;样本容量:50.
26.解:完成表格得
姓名
王芳
刘兵
张昕
李聪
江文
成绩
89
92
90
84
88
与全班平均分之差
﹣1
+2
0
﹣6
﹣2
故答案为分数最高的是刘兵,分数最低的是李聪,张昕的分数与全班平均分最接近.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
