人教版八年级数学上册第十一章11.1.2三角形的高、中线与角平分线 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学上册第十一章11.1.2三角形的高、中线与角平分线 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 09:50:52 | ||
图片预览







文档简介
(共22张PPT)
11.1.2
三角形的高、中线与角平分线
教学目标
三角形的高、中线与角平分线的定义.
对直角三角形和钝角三角形的三条高的认识和理解.
2.过一点如何做已知线段的垂线?
在下面试着画一画
.
学习●研讨
知识点1:三角形的高
(1)定义
的线条叫做三角形的高线,简称三角形的高.
三角形的高有三条,特别地.三角形的高不一定在三角形内部.三角形的三条高交于一点.叫三角形的垂心
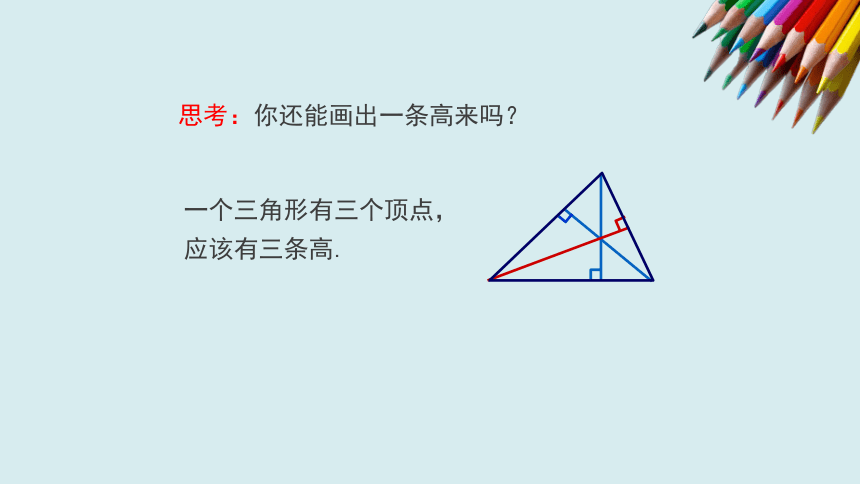
思考:你还能画出一条高来吗?
一个三角形有三个顶点,应该有三条高.
归纳:锐角三角形有
条高,它们相交于一点,交点在三角形
,.钝角三角形有
高,它们相交于一点,交点在三角形
。直角三角形有
,它们相交于一点交点在
。
注意:三角形的高是线段
(几何语言)
∵AD是ΔABC上的高
∴AD⊥BC
(∠ADB=∠ADC=90)
逆向:∵AD⊥BC垂足是D
∴AD是ΔABC的边
BC
上的高
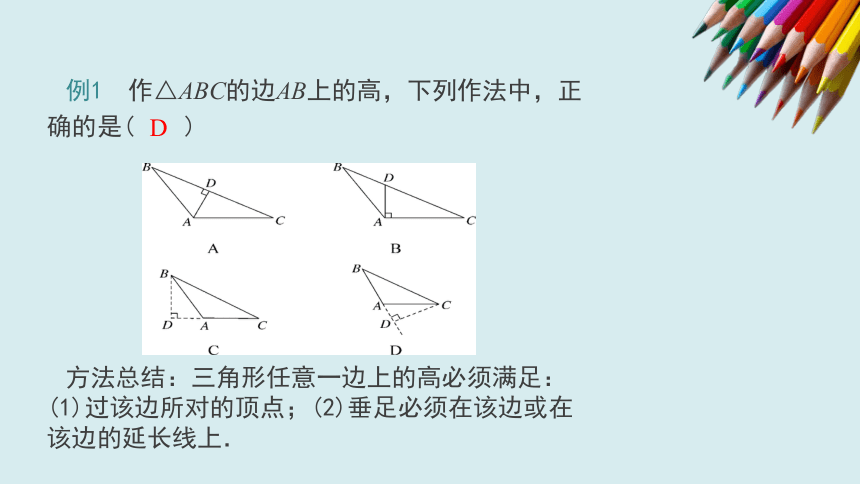
例1
作△ABC的边AB上的高,下列作法中,正确的是( )
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例2
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
三角形的三条中线交于一点,这个交点就是
三角形的重心.
例3
在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
提示:将△ABD与△ADC的周长之差转化为边长的差.
7cm
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,
∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°-∠B-∠BAD
=180°-36°-34°=110°.
例4
如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
3.如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有
( )
A.2条
B.3条
C.4条
D.5条
4.下列各组图形中,哪一组图形中AD是△ABC
的BC边上的高
(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2______.
图①
图②
AF
DC
∠2
2∠4
AC
∠ABC
课堂小结
1.三角形的三条重要线段:高线、中线、角平分线.
2.三角形的稳定性.
通过本课时的学习,需要我们掌握:
11.1.2
三角形的高、中线与角平分线
教学目标
三角形的高、中线与角平分线的定义.
对直角三角形和钝角三角形的三条高的认识和理解.
2.过一点如何做已知线段的垂线?
在下面试着画一画
.
学习●研讨
知识点1:三角形的高
(1)定义
的线条叫做三角形的高线,简称三角形的高.
三角形的高有三条,特别地.三角形的高不一定在三角形内部.三角形的三条高交于一点.叫三角形的垂心
思考:你还能画出一条高来吗?
一个三角形有三个顶点,应该有三条高.
归纳:锐角三角形有
条高,它们相交于一点,交点在三角形
,.钝角三角形有
高,它们相交于一点,交点在三角形
。直角三角形有
,它们相交于一点交点在
。
注意:三角形的高是线段
(几何语言)
∵AD是ΔABC上的高
∴AD⊥BC
(∠ADB=∠ADC=90)
逆向:∵AD⊥BC垂足是D
∴AD是ΔABC的边
BC
上的高
例1
作△ABC的边AB上的高,下列作法中,正确的是( )
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例2
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
三角形的三条中线交于一点,这个交点就是
三角形的重心.
例3
在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
提示:将△ABD与△ADC的周长之差转化为边长的差.
7cm
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,
∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°-∠B-∠BAD
=180°-36°-34°=110°.
例4
如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
3.如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有
( )
A.2条
B.3条
C.4条
D.5条
4.下列各组图形中,哪一组图形中AD是△ABC
的BC边上的高
(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
5.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2______.
图①
图②
AF
DC
∠2
2∠4
AC
∠ABC
课堂小结
1.三角形的三条重要线段:高线、中线、角平分线.
2.三角形的稳定性.
通过本课时的学习,需要我们掌握:
