13.3全等三角形的判定 同步培优提升训练 2021-2022学年冀教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 13.3全等三角形的判定 同步培优提升训练 2021-2022学年冀教版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 355.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 09:16:48 | ||
图片预览

文档简介
2021-2022学年冀教版八年级数学上册《13.3全等三角形的判定》
同步培优提升训练(附答案)
一.选择题
1.已知D是△ABC的边AB上一点,DF交AC于点E,DE=EF,FC∥AB,若BD=2,CF=5,则AB的长为( )
A.1
B.3
C.5
D.7
2.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC一定全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
3.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4
B.3
C.2
D.1
4.如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F.请你添加一个适当的条件,使△AEF≌△CEB.下列添加的条件不正确的是( )
A.EF=EB
B.EA=EC
C.AF=CB
D.∠AFE=∠B
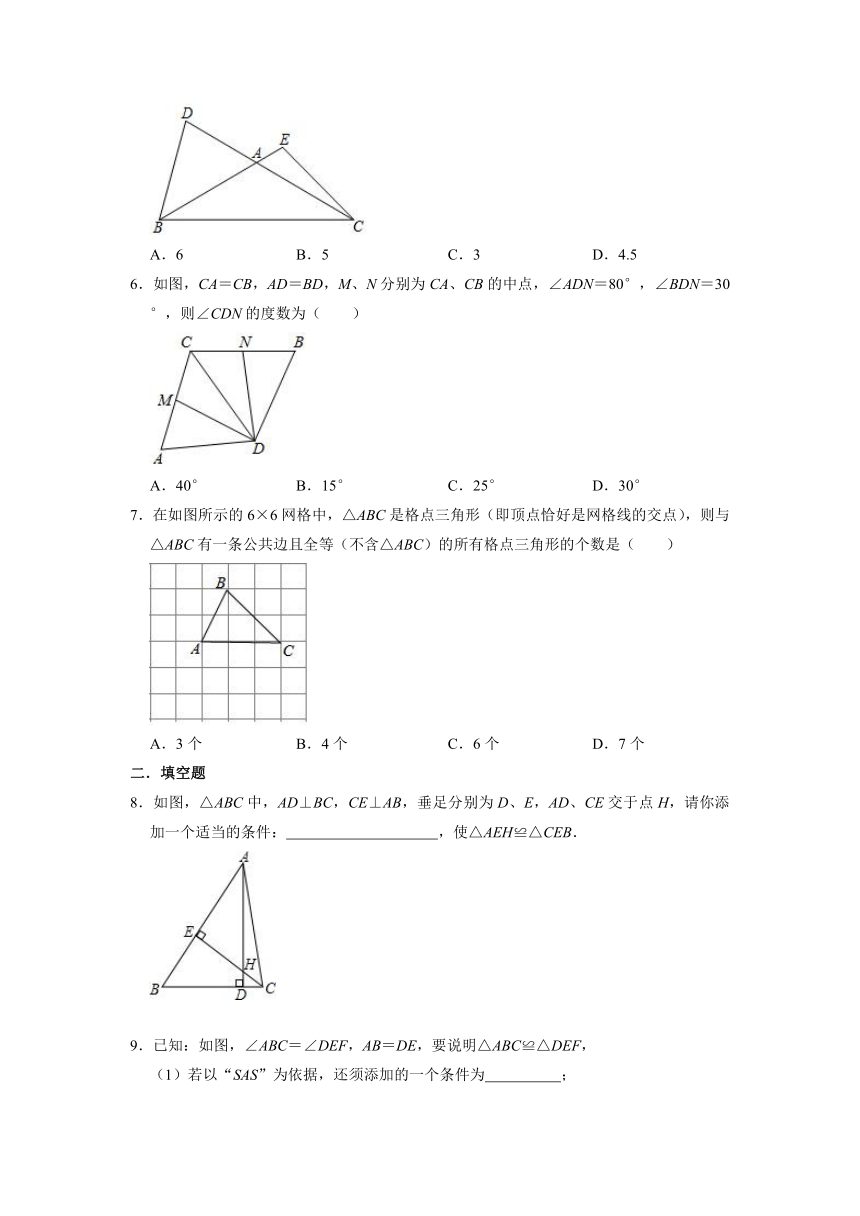
5.如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )
A.6
B.5
C.3
D.4.5
6.如图,CA=CB,AD=BD,M、N分别为CA、CB的中点,∠ADN=80°,∠BDN=30°,则∠CDN的度数为( )
A.40°
B.15°
C.25°
D.30°
7.在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是( )
A.3个
B.4个
C.6个
D.7个
二.填空题
8.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:
,使△AEH≌△CEB.
9.已知:如图,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,
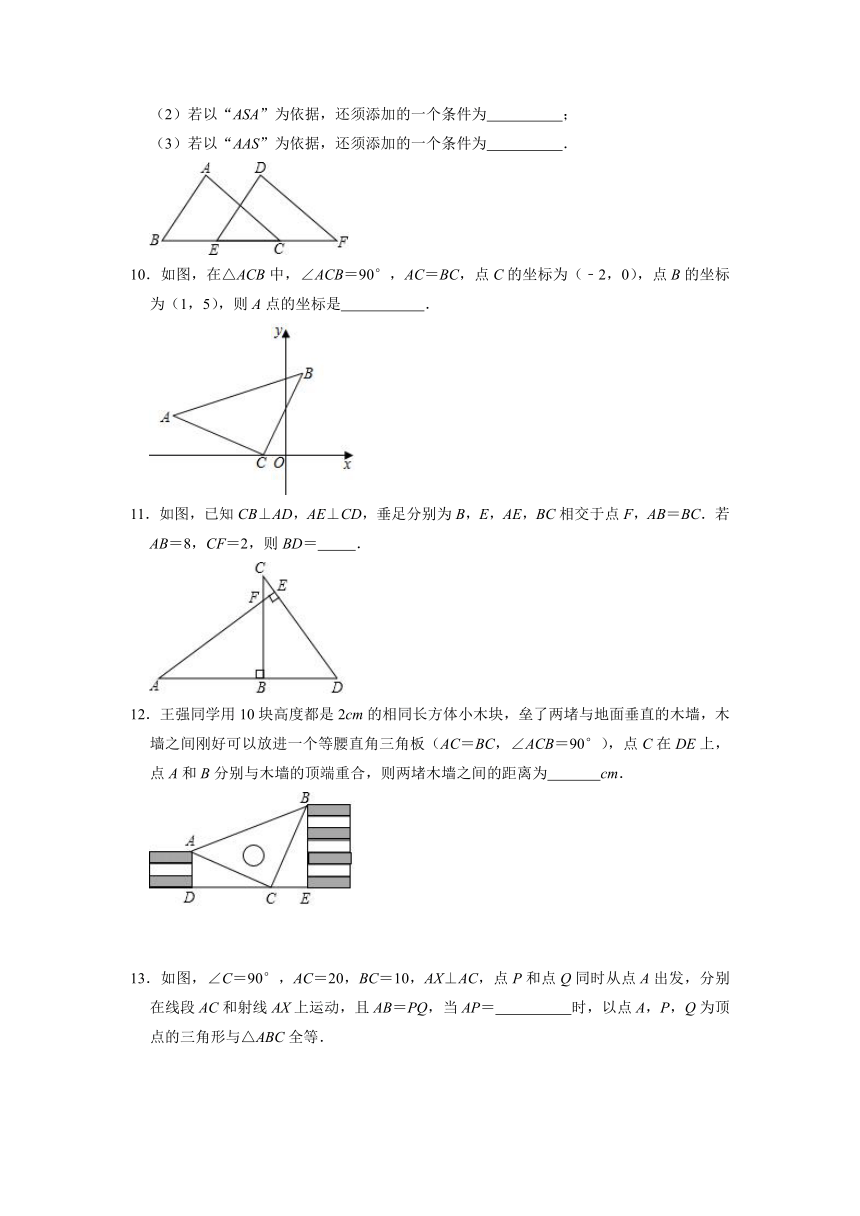
(1)若以“SAS”为依据,还须添加的一个条件为
;
(2)若以“ASA”为依据,还须添加的一个条件为
;
(3)若以“AAS”为依据,还须添加的一个条件为
.
10.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点B的坐标为(1,5),则A点的坐标是
.
11.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E,AE,BC相交于点F,AB=BC.若AB=8,CF=2,则BD=
.
12.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为
cm.
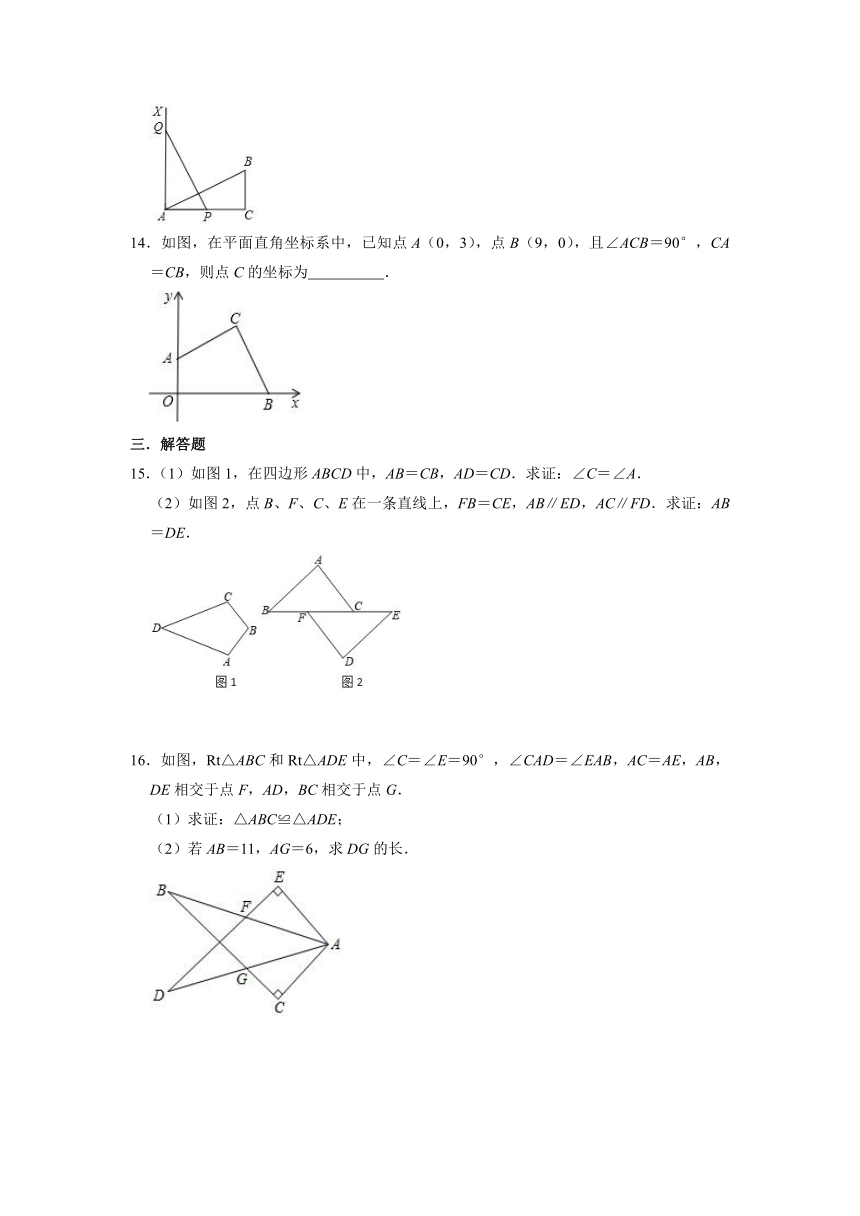
13.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当AP=
时,以点A,P,Q为顶点的三角形与△ABC全等.
14.如图,在平面直角坐标系中,已知点A(0,3),点B(9,0),且∠ACB=90°,CA=CB,则点C的坐标为
.
三.解答题
15.(1)如图1,在四边形ABCD中,AB=CB,AD=CD.求证:∠C=∠A.
(2)如图2,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AB=DE.
16.如图,Rt△ABC和Rt△ADE中,∠C=∠E=90°,∠CAD=∠EAB,AC=AE,AB,DE相交于点F,AD,BC相交于点G.
(1)求证:△ABC≌△ADE;
(2)若AB=11,AG=6,求DG的长.
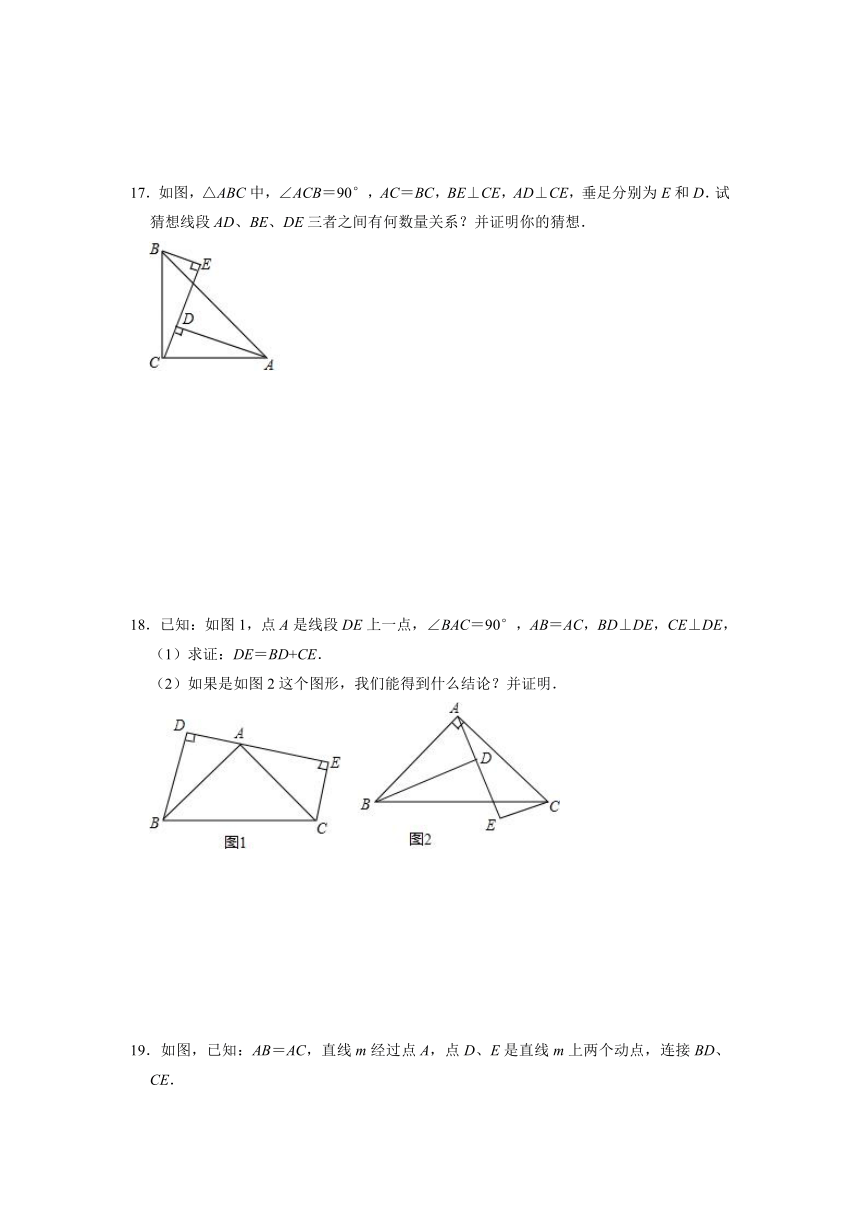
17.如图,△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E和D.试猜想线段AD、BE、DE三者之间有何数量关系?并证明你的猜想.
18.已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
19.如图,已知:AB=AC,直线m经过点A,点D、E是直线m上两个动点,连接BD、CE.
(1)如图1,若∠BAC=90°,BD⊥DE,CE⊥DE.求证:DE=BD+CE.
(2)如图2,若∠BAC=∠BDA=∠AEC,则(1)中的结论DE=BD+CE还成立吗?(只回答,不用证明)
(3)如图3,在(2)的条件下,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,是判定△DEF的形状,并证明你的判定.
20.问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为
.
21.如图,AB∥CD,点E在CB的延长线上,∠A=∠E,AC=ED.
(1)求证:BC=CD;
(2)连接BD,求证:∠ABD=∠EBD.
22.在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌△AFE;
(2)AD=AB+CD.
参考答案
1.解:∵FC∥AB,
∴∠ADF=∠F.
∵∠AED=∠CEF,DE=EF,
∴△ADE≌△CEF(ASA).
∴AD=CF=5.
又∵BD=2,
∴AB=AD+BD=5+2=7,
故选:D.
2.解:乙和△ABC全等;理由如下:
在△ABC和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和图丙的三角形中,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
不能判定甲与△ABC全等;
故选:B.
3.解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,故②正确;
∵∠OAC=∠OBD,
由三角形的外角性质得:
∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°,故①正确;
法一:作OG⊥AM于G,OH⊥DM于H,如图所示,
则∠OGA=∠OHB=90°,
∵△AOC≌△BOD,
∴OG=OH,
∴MO平分∠AMD,故④正确;
法二:∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∴A、B、M、O四点共圆,
∴∠AMO=∠ABO=72°,
同理可得:D、C、M、O四点共圆,
∴∠DMO=∠DCO=72°=∠AMO,
∴MO平分∠AMD,
故④正确;
假设MO平分∠AOD,则∠DOM=∠AOM,
在△AMO与△DMO中,
,
∴△AMO≌△DMO(ASA),
∴AO=OD,
∵OC=OD,
∴OA=OC,
而OA<OC,故③错误;
正确的个数有3个;
故选:B.
4.解:∵AD⊥BC于D,CE⊥AB于E,
∴∠AEF=∠CEB=90°,
在Rt△AEF和Rt△CDF中,∵∠AFE=∠CFD,
∴90°﹣∠AFE=90°﹣∠CFD,
∴∠EAF=∠DCF,
所以根据AAS添加EF=EB或AF=CB,根据ASA添加EA=EC,可证△AEF≌△CEB.
故选:D.
5.解:如图,延长BE使AF=AD,连接CF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴∠F=∠D,BD=CF=6,
∵∠D+∠BEC=180°,∠BEC+∠FEC=180°,
∴∠D=∠FEC,
∴∠F=∠FEC,
∴CF=CE=6,
故选:A.
6.解:在△CAD和△CBD中,
,
∴△CAD≌△CBD(SSS),
∴∠CDA=∠CDB,∠A=∠B,
又∵AC=CB,M,N分别为CA,CB的中点,
∴AM=BN,又AD=BD,
∴△ADM≌△BDN(SAS),
∴∠ADM=∠BDN=30°,
∵∠ADN=80°,
∴∠ADM+2∠CDN=80°,
∴∠CDN=25°,
故选:C.
7.解:如图所示:一共有7个符合题意的点.
故选:D.
8.解:∵AD⊥BC,CE⊥AB,垂足分别为D、E,
∴∠BEC=∠AEC=90°,
在Rt△AEH中,∠EAH=90°﹣∠AHE,
又∵∠EAH=∠BAD,
∴∠BAD=90°﹣∠AHE,
在Rt△AEH和Rt△CDH中,∠CHD=∠AHE,
∴∠EAH=∠DCH,
∴∠EAH=90°﹣∠CHD=∠BCE,
所以根据AAS添加AH=CB或EH=EB;
根据ASA添加AE=CE.
可证△AEH≌△CEB.
故填空答案:AH=CB或EH=EB或AE=CE.
9.解:(1)若以“SAS”为依据,还须添加的一个条件为BC=EF;
(2)若以“ASA”为依据,还须添加的一个条件为∠A=∠D;
(3)若以“AAS”为依据,还须添加的一个条件为∠ACB=∠DFE.
故填BC=EF,∠A=∠D,∠ACB=∠DFE.
10.解:如图,过A作AD⊥OC于D,过点B作BE⊥OC于E,
∵点C的坐标为(﹣2,0),点B的坐标为(1,5),
∴OC=2,OE=1,BE=5,
∵∠ACB=90°,
∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴DC=BE=5,AD=CE=1+2=3,
∴OD=2+5=7,
∴则A点的坐标是(﹣7,3).
故答案为(﹣7,3).
11.证明:∵CB⊥AD,AE⊥CD,
∴∠ABF=∠CBD=∠AED=90°,
∴∠A+∠D=∠C+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中,,
∴△ABF≌△CBD(ASA),
∴BF=BD,
∵BC=AB=8,BF=BC﹣CF=8﹣2=6,
∴BD=BF=6;
故答案为:6.
12.解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
13.解:∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90°,
分两种情况:
①当AP=BC=10时,
在Rt△ABC和Rt△QPA中,
,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=20时,
在△ABC和△PQA中,
,
∴Rt△ABC≌Rt△PQA(HL);
综上所述:当点P运动到AP=10或20时,△ABC与△APQ全等;
故答案为:10或20.
14.解:如图,过点C作CE⊥OA,CF⊥OB,
∵∠AOB=90°,
∴四边形OECF是矩形,
∴∠ECF=90°,
∵∠ACB=90°,
∴∠ACE=∠BCF,
在△ACE和△BCF中,,
∴△ACE≌△BCF,
∴CE=CF,
∵四边形OECF是矩形,
∴矩形OECF是正方形,
∴OE=OF,
∵AE=OE﹣OA=OE﹣3,BF=OB﹣OF=9﹣OF,
∴OE=OF=6,
∴C(6,6),
故答案为:(6,6);
15.证明:(1)如图1中,连接BD.
在△BDC和△BDA中,
,
∴△BDC≌△BDA(SSS),
∴∠C=∠A.
(2)如图2中,
∵FB=CE,
∴BC=EF,
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠EFD,
在△ABC和△DEF中,
,
∴△ACB≌△DFE(ASA),
∴AB=DE.
16.(1)证明:∵∠CAD=∠EAB,
∴∠CAD+∠BAD=∠EAB+∠DAB,即∠CAB=∠EAD.
又AC=AE,∠C=∠E=90°,
∴△ABC≌△ADE(ASA);
(2)∵△ABC≌△ADE,
∴AB=AD.
∵AB=11,
∴AD=11.
又AG=6,
∴DG=11﹣6=5.
17.答:AD﹣BE=DE,
证明:∵∠E=∠CDA=∠ACB=90°,
∴∠BCE+∠ACD=90°,∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△BCE和△CAD中,
,
∴△BCE≌△CAD,
∴BE=CD,AD=CE,
∴AD﹣BE=CE﹣CD=DE.
18.证明:(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∴DE=AD+AE=CE+BD;
(2)BD=DE+CE,理由是:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠ABD+∠EAC=90°,
∴∠BAD=∠EAC,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
19.解:(1)∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵BD⊥AD,
∴∠BDA=90°,
∴∠BAD+∠ABD=90°,
∴∠DBA=∠CAE;
∵CE⊥DE,
∴∠CEA=90°,
∴∠ADB=∠CEA.
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS)
∴AD=CE,BD=AE.
∵DE=DA+AE,
∴DE=BD+CE;
(2)(1)中的结论DE=BD+CE仍然成立.
理由:∵∠DAB+BAC+∠CAE=180°,∠CAE+∠ACE+∠AEC=180°,
∴∠DAB+∠BAC+∠CAE=∠CAE+∠ACE+∠AEC.
∵∠BAC=∠AEC,
∴∠DAB=∠ACE.
在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS)
∴AD=CE,BD=AE.
∵DE=DA+AE,
∴DE=BD+CE;
(3)△DFE是等边三角形.
理由:∵△ADB≌△CEA,
∴∠DBA=∠EAC,BD=EA.
∵△ABF和△ACF均为等边三角形,
∴BF=AB=AF=AC=CF,∠ABF=∠CAF=60°,
∴∠ABF+∠DBA=∠CAF+∠EAC,
∴∠DBF=∠EAF.
在△FDB和△FEA中,
,
∴△FDB≌△FEA(SAS),
∴DF=EF,∠DFB=∠EFA.
∵∠DFB+∠DFA=60°,
∴∠EFA+∠DFA=60°,
即∠DFE=60°
∴△DFE是等边三角形.
20.证明:图②,
∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
∵,
∴△ABD≌△CAF(AAS);
图③,
∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
∵,
∴△ABE≌△CAF(ASA);
图④,
解:∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是:×15=5,
由图3中证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积,是5,
故答案为:5.
21.证明:(1)∵AB∥CD,
∴∠ABC=∠DCE,
在△ABC和△ECD中,
,
∴△ABC≌△ECD(AAS),
∴BC=CD;
(2)如图,连接BD,
∵BC=CD,
∴∠CBD=∠CDB,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
又∵∠CBD+∠EBD=180°,
∴∠ABD=∠EBD.
22.(1)证明:∵AE平分∠BAD,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SAS);
(2)证明:由(1)知,△ABE≌△AFE,
∴EB=EF,∠AEB=∠AEF,
∵∠BEC=180°,∠AED=90°,
∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,
∵点E为BC的中点,
∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,
,
∴△ECD≌△EFD(SAS),
∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
同步培优提升训练(附答案)
一.选择题
1.已知D是△ABC的边AB上一点,DF交AC于点E,DE=EF,FC∥AB,若BD=2,CF=5,则AB的长为( )
A.1
B.3
C.5
D.7
2.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC一定全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
3.如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:
①∠AMB=36°,②AC=BD,③OM平分∠AOD,④MO平分∠AMD.其中正确的结论个数有( )个.
A.4
B.3
C.2
D.1
4.如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F.请你添加一个适当的条件,使△AEF≌△CEB.下列添加的条件不正确的是( )
A.EF=EB
B.EA=EC
C.AF=CB
D.∠AFE=∠B
5.如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )
A.6
B.5
C.3
D.4.5
6.如图,CA=CB,AD=BD,M、N分别为CA、CB的中点,∠ADN=80°,∠BDN=30°,则∠CDN的度数为( )
A.40°
B.15°
C.25°
D.30°
7.在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是( )
A.3个
B.4个
C.6个
D.7个
二.填空题
8.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:
,使△AEH≌△CEB.
9.已知:如图,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,
(1)若以“SAS”为依据,还须添加的一个条件为
;
(2)若以“ASA”为依据,还须添加的一个条件为
;
(3)若以“AAS”为依据,还须添加的一个条件为
.
10.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点B的坐标为(1,5),则A点的坐标是
.
11.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E,AE,BC相交于点F,AB=BC.若AB=8,CF=2,则BD=
.
12.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为
cm.
13.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当AP=
时,以点A,P,Q为顶点的三角形与△ABC全等.
14.如图,在平面直角坐标系中,已知点A(0,3),点B(9,0),且∠ACB=90°,CA=CB,则点C的坐标为
.
三.解答题
15.(1)如图1,在四边形ABCD中,AB=CB,AD=CD.求证:∠C=∠A.
(2)如图2,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AB=DE.
16.如图,Rt△ABC和Rt△ADE中,∠C=∠E=90°,∠CAD=∠EAB,AC=AE,AB,DE相交于点F,AD,BC相交于点G.
(1)求证:△ABC≌△ADE;
(2)若AB=11,AG=6,求DG的长.
17.如图,△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E和D.试猜想线段AD、BE、DE三者之间有何数量关系?并证明你的猜想.
18.已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
19.如图,已知:AB=AC,直线m经过点A,点D、E是直线m上两个动点,连接BD、CE.
(1)如图1,若∠BAC=90°,BD⊥DE,CE⊥DE.求证:DE=BD+CE.
(2)如图2,若∠BAC=∠BDA=∠AEC,则(1)中的结论DE=BD+CE还成立吗?(只回答,不用证明)
(3)如图3,在(2)的条件下,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,是判定△DEF的形状,并证明你的判定.
20.问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图4,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为
.
21.如图,AB∥CD,点E在CB的延长线上,∠A=∠E,AC=ED.
(1)求证:BC=CD;
(2)连接BD,求证:∠ABD=∠EBD.
22.在四边形ABCD中,E为BC边中点.已知:如图,若AE平分∠BAD,∠AED=90°,点F为AD上一点,AF=AB.
求证:(1)△ABE≌△AFE;
(2)AD=AB+CD.
参考答案
1.解:∵FC∥AB,
∴∠ADF=∠F.
∵∠AED=∠CEF,DE=EF,
∴△ADE≌△CEF(ASA).
∴AD=CF=5.
又∵BD=2,
∴AB=AD+BD=5+2=7,
故选:D.
2.解:乙和△ABC全等;理由如下:
在△ABC和图乙的三角形中,满足三角形全等的判定方法:SAS,
所以乙和△ABC全等;
在△ABC和图丙的三角形中,满足三角形全等的判定方法:AAS,
所以丙和△ABC全等;
不能判定甲与△ABC全等;
故选:B.
3.解:∵∠AOB=∠COD=36°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,故②正确;
∵∠OAC=∠OBD,
由三角形的外角性质得:
∠AMB+∠OBD=∠OAC+∠AOB,
∴∠AMB=∠AOB=36°,故①正确;
法一:作OG⊥AM于G,OH⊥DM于H,如图所示,
则∠OGA=∠OHB=90°,
∵△AOC≌△BOD,
∴OG=OH,
∴MO平分∠AMD,故④正确;
法二:∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∴A、B、M、O四点共圆,
∴∠AMO=∠ABO=72°,
同理可得:D、C、M、O四点共圆,
∴∠DMO=∠DCO=72°=∠AMO,
∴MO平分∠AMD,
故④正确;
假设MO平分∠AOD,则∠DOM=∠AOM,
在△AMO与△DMO中,
,
∴△AMO≌△DMO(ASA),
∴AO=OD,
∵OC=OD,
∴OA=OC,
而OA<OC,故③错误;
正确的个数有3个;
故选:B.
4.解:∵AD⊥BC于D,CE⊥AB于E,
∴∠AEF=∠CEB=90°,
在Rt△AEF和Rt△CDF中,∵∠AFE=∠CFD,
∴90°﹣∠AFE=90°﹣∠CFD,
∴∠EAF=∠DCF,
所以根据AAS添加EF=EB或AF=CB,根据ASA添加EA=EC,可证△AEF≌△CEB.
故选:D.
5.解:如图,延长BE使AF=AD,连接CF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴∠F=∠D,BD=CF=6,
∵∠D+∠BEC=180°,∠BEC+∠FEC=180°,
∴∠D=∠FEC,
∴∠F=∠FEC,
∴CF=CE=6,
故选:A.
6.解:在△CAD和△CBD中,
,
∴△CAD≌△CBD(SSS),
∴∠CDA=∠CDB,∠A=∠B,
又∵AC=CB,M,N分别为CA,CB的中点,
∴AM=BN,又AD=BD,
∴△ADM≌△BDN(SAS),
∴∠ADM=∠BDN=30°,
∵∠ADN=80°,
∴∠ADM+2∠CDN=80°,
∴∠CDN=25°,
故选:C.
7.解:如图所示:一共有7个符合题意的点.
故选:D.
8.解:∵AD⊥BC,CE⊥AB,垂足分别为D、E,
∴∠BEC=∠AEC=90°,
在Rt△AEH中,∠EAH=90°﹣∠AHE,
又∵∠EAH=∠BAD,
∴∠BAD=90°﹣∠AHE,
在Rt△AEH和Rt△CDH中,∠CHD=∠AHE,
∴∠EAH=∠DCH,
∴∠EAH=90°﹣∠CHD=∠BCE,
所以根据AAS添加AH=CB或EH=EB;
根据ASA添加AE=CE.
可证△AEH≌△CEB.
故填空答案:AH=CB或EH=EB或AE=CE.
9.解:(1)若以“SAS”为依据,还须添加的一个条件为BC=EF;
(2)若以“ASA”为依据,还须添加的一个条件为∠A=∠D;
(3)若以“AAS”为依据,还须添加的一个条件为∠ACB=∠DFE.
故填BC=EF,∠A=∠D,∠ACB=∠DFE.
10.解:如图,过A作AD⊥OC于D,过点B作BE⊥OC于E,
∵点C的坐标为(﹣2,0),点B的坐标为(1,5),
∴OC=2,OE=1,BE=5,
∵∠ACB=90°,
∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴DC=BE=5,AD=CE=1+2=3,
∴OD=2+5=7,
∴则A点的坐标是(﹣7,3).
故答案为(﹣7,3).
11.证明:∵CB⊥AD,AE⊥CD,
∴∠ABF=∠CBD=∠AED=90°,
∴∠A+∠D=∠C+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中,,
∴△ABF≌△CBD(ASA),
∴BF=BD,
∵BC=AB=8,BF=BC﹣CF=8﹣2=6,
∴BD=BF=6;
故答案为:6.
12.解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
13.解:∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90°,
分两种情况:
①当AP=BC=10时,
在Rt△ABC和Rt△QPA中,
,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=20时,
在△ABC和△PQA中,
,
∴Rt△ABC≌Rt△PQA(HL);
综上所述:当点P运动到AP=10或20时,△ABC与△APQ全等;
故答案为:10或20.
14.解:如图,过点C作CE⊥OA,CF⊥OB,
∵∠AOB=90°,
∴四边形OECF是矩形,
∴∠ECF=90°,
∵∠ACB=90°,
∴∠ACE=∠BCF,
在△ACE和△BCF中,,
∴△ACE≌△BCF,
∴CE=CF,
∵四边形OECF是矩形,
∴矩形OECF是正方形,
∴OE=OF,
∵AE=OE﹣OA=OE﹣3,BF=OB﹣OF=9﹣OF,
∴OE=OF=6,
∴C(6,6),
故答案为:(6,6);
15.证明:(1)如图1中,连接BD.
在△BDC和△BDA中,
,
∴△BDC≌△BDA(SSS),
∴∠C=∠A.
(2)如图2中,
∵FB=CE,
∴BC=EF,
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠EFD,
在△ABC和△DEF中,
,
∴△ACB≌△DFE(ASA),
∴AB=DE.
16.(1)证明:∵∠CAD=∠EAB,
∴∠CAD+∠BAD=∠EAB+∠DAB,即∠CAB=∠EAD.
又AC=AE,∠C=∠E=90°,
∴△ABC≌△ADE(ASA);
(2)∵△ABC≌△ADE,
∴AB=AD.
∵AB=11,
∴AD=11.
又AG=6,
∴DG=11﹣6=5.
17.答:AD﹣BE=DE,
证明:∵∠E=∠CDA=∠ACB=90°,
∴∠BCE+∠ACD=90°,∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△BCE和△CAD中,
,
∴△BCE≌△CAD,
∴BE=CD,AD=CE,
∴AD﹣BE=CE﹣CD=DE.
18.证明:(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∴DE=AD+AE=CE+BD;
(2)BD=DE+CE,理由是:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠ABD+∠EAC=90°,
∴∠BAD=∠EAC,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
19.解:(1)∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵BD⊥AD,
∴∠BDA=90°,
∴∠BAD+∠ABD=90°,
∴∠DBA=∠CAE;
∵CE⊥DE,
∴∠CEA=90°,
∴∠ADB=∠CEA.
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS)
∴AD=CE,BD=AE.
∵DE=DA+AE,
∴DE=BD+CE;
(2)(1)中的结论DE=BD+CE仍然成立.
理由:∵∠DAB+BAC+∠CAE=180°,∠CAE+∠ACE+∠AEC=180°,
∴∠DAB+∠BAC+∠CAE=∠CAE+∠ACE+∠AEC.
∵∠BAC=∠AEC,
∴∠DAB=∠ACE.
在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS)
∴AD=CE,BD=AE.
∵DE=DA+AE,
∴DE=BD+CE;
(3)△DFE是等边三角形.
理由:∵△ADB≌△CEA,
∴∠DBA=∠EAC,BD=EA.
∵△ABF和△ACF均为等边三角形,
∴BF=AB=AF=AC=CF,∠ABF=∠CAF=60°,
∴∠ABF+∠DBA=∠CAF+∠EAC,
∴∠DBF=∠EAF.
在△FDB和△FEA中,
,
∴△FDB≌△FEA(SAS),
∴DF=EF,∠DFB=∠EFA.
∵∠DFB+∠DFA=60°,
∴∠EFA+∠DFA=60°,
即∠DFE=60°
∴△DFE是等边三角形.
20.证明:图②,
∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
∵,
∴△ABD≌△CAF(AAS);
图③,
∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,
在△ABE和△CAF中,
∵,
∴△ABE≌△CAF(ASA);
图④,
解:∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是:×15=5,
由图3中证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积,是5,
故答案为:5.
21.证明:(1)∵AB∥CD,
∴∠ABC=∠DCE,
在△ABC和△ECD中,
,
∴△ABC≌△ECD(AAS),
∴BC=CD;
(2)如图,连接BD,
∵BC=CD,
∴∠CBD=∠CDB,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
又∵∠CBD+∠EBD=180°,
∴∠ABD=∠EBD.
22.(1)证明:∵AE平分∠BAD,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SAS);
(2)证明:由(1)知,△ABE≌△AFE,
∴EB=EF,∠AEB=∠AEF,
∵∠BEC=180°,∠AED=90°,
∴∠AEB+∠DEC=90°,∠AEF+∠DEF=90°,
∴∠DEC=∠DEF,
∵点E为BC的中点,
∴EB=EC,
∴EF=EC,
在△ECD和△EFD中,
,
∴△ECD≌△EFD(SAS),
∴DC=DF,
∵AD=AF+DF,AB=AF,
∴AD=AB+CD.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
