冀教版七年级数学上册第二章几何图形的初步认识 练习题 (word版,含答案)
文档属性
| 名称 | 冀教版七年级数学上册第二章几何图形的初步认识 练习题 (word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 241.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 11:42:47 | ||
图片预览



文档简介
数学
第二章 几何图形的初步认识
类型之一 立体图形的识别与分类
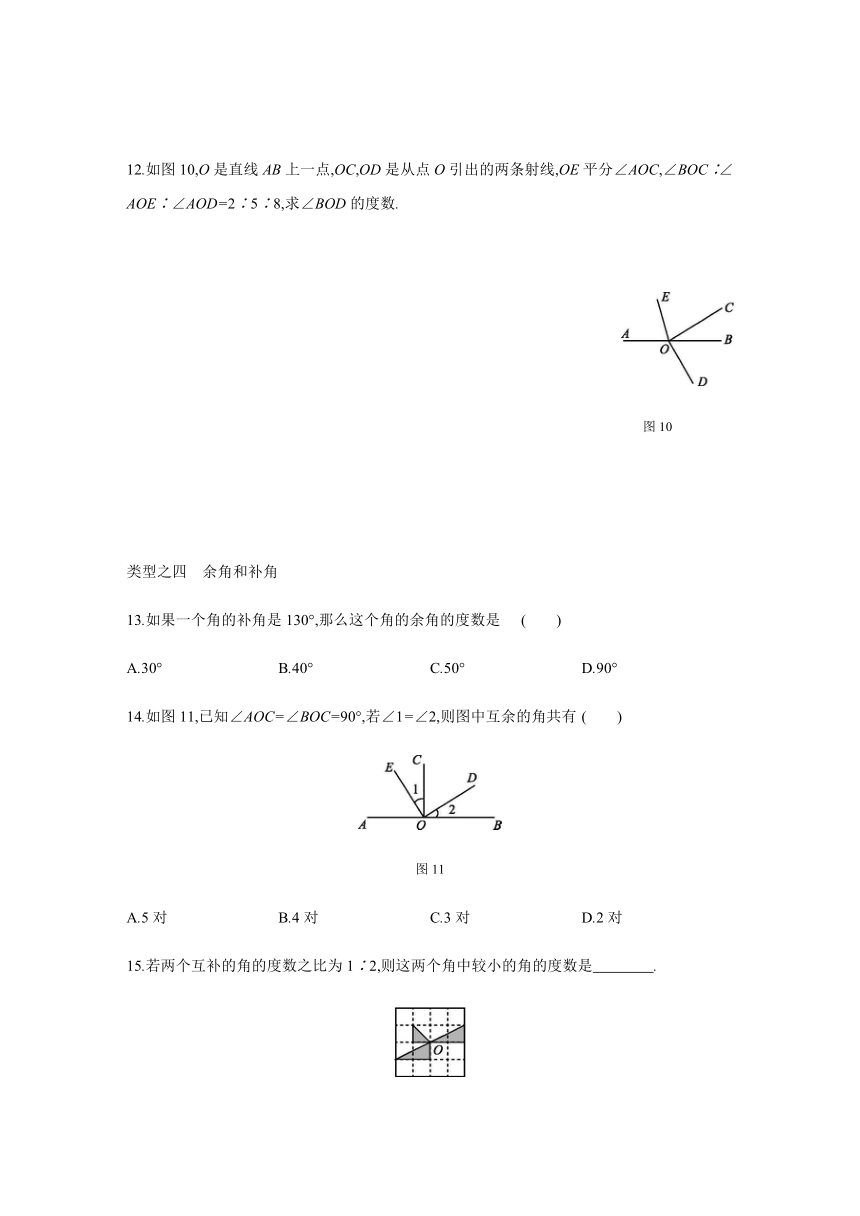
1.对如图1所示的几何体的认识正确的是
( )
图1
A.该棱柱的底面是四边形
B.该棱柱有四个面
C.该几何体是四棱柱
D.该棱柱的底面是三角形
2.下列几何体中,属于柱体的有
( )
图2
A.5个
B.4个
C.3个
D.2个
3.下列几何体中,含有曲面的是 .(填名称)?
图3
类型之二 用数学知识解释现实生活中的实际问题
4.雨滴滴下来形成雨丝,这一现象说明
( )
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
5.如图4,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线.能解释这一实际应用的数学知识是 .?
图4
6.如图5所示,在一条笔直公路l的两侧,分别有A,B两个小区,为了方便居民出行,现要在公路l上建一个公共自行车存放点,使存放点到A,B两个小区的距离之和最小,你认为存放点应该建在 处(填“C”“E”或“D”),理由是 .?
图5
类型之三 线段和角的计算
7.如图6所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是
( )
图6
A.20°
B.25°
C.30°
D.70°
8.如图7,已知M是线段AB的中点,N是线段AM上的点,且满足AN∶MN=1∶2.若AN=2
cm,则AB的长度是
( )
图7
A.6
cm
B.8
cm
C.10
cm
D.12
cm
9.56°48'= °,4.3°= ° '.?
10.如图8,已知线段AB=3
cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线上取一点D,使AD=AB.
(1)求线段BC,DC的长;
(2)K是哪些线段的中点?
图8
11.如图9,∠AOB=110°,∠COD=70°,OA平分∠EOC,OB平分∠DOF,求∠EOF的度数.
图9
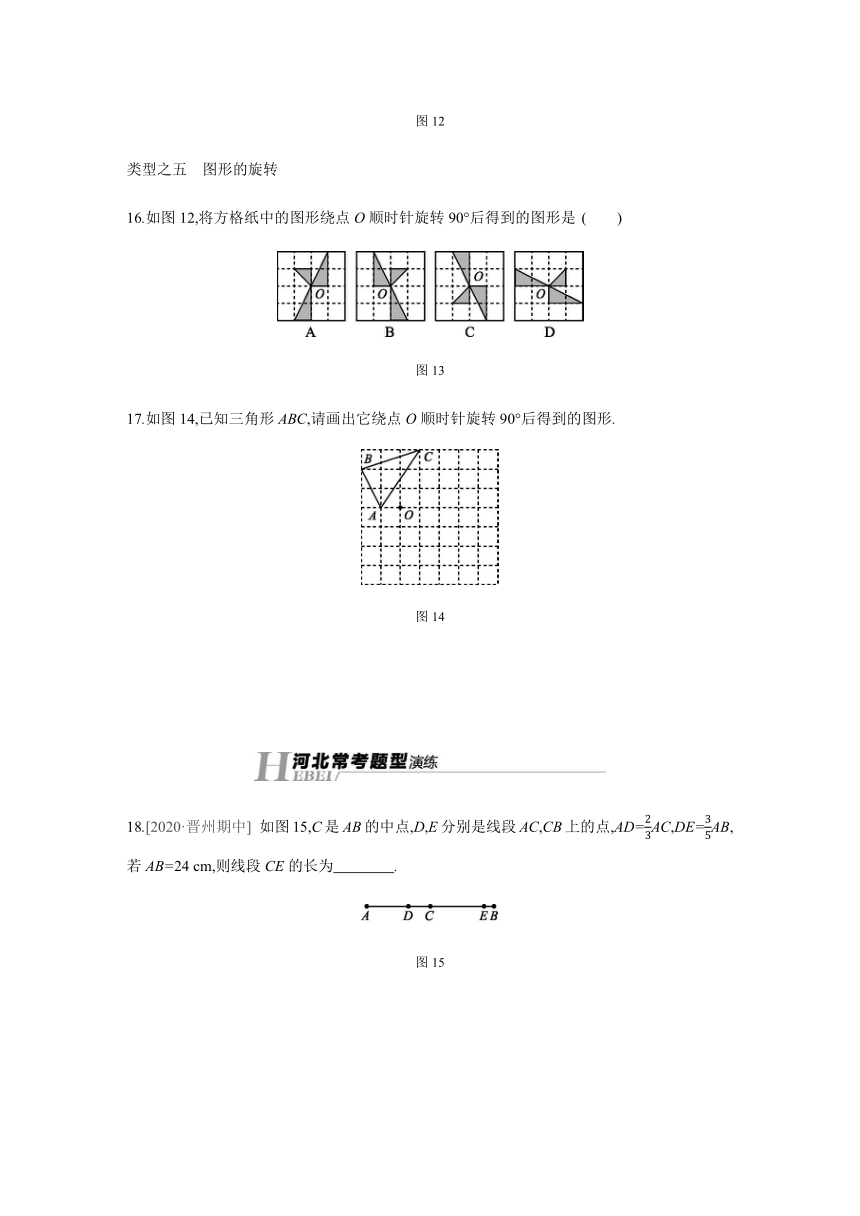
12.如图10,O是直线AB上一点,OC,OD是从点O引出的两条射线,OE平分∠AOC,∠BOC∶∠AOE∶∠AOD=2∶5∶8,求∠BOD的度数.
图10
类型之四 余角和补角
13.如果一个角的补角是130°,那么这个角的余角的度数是
( )
A.30°
B.40°
C.50°
D.90°
14.如图11,已知∠AOC=∠BOC=90°,若∠1=∠2,则图中互余的角共有
( )
图11
A.5对
B.4对
C.3对
D.2对
15.若两个互补的角的度数之比为1∶2,则这两个角中较小的角的度数是 .?
图12
类型之五 图形的旋转
16.如图12,将方格纸中的图形绕点O顺时针旋转90°后得到的图形是
( )
图13
17.如图14,已知三角形ABC,请画出它绕点O顺时针旋转90°后得到的图形.
图14
18.[2020·晋州期中]
如图15,C是AB的中点,D,E分别是线段AC,CB上的点,AD=AC,DE=AB,若AB=24
cm,则线段CE的长为 .?
图15
19.[2020·遵化期中]
如图16,已知O为直线AB上的一点,∠BOC=∠DOE=90°.
(1)如图(a),当射线OC,OD在直线AB的两侧时,请回答下列问题,并说明理由.
①∠COD和∠BOE相等吗?
②∠BOD和∠COE有什么数量关系?
(2)如图(b),当射线OC,OD在直线AB的同侧时,请直接回答下列问题.
①∠COD和∠BOE相等吗?
②(1)②中的∠BOD和∠COE的关系还成立吗?
(a) (b)
图16
答案
1.D [解析]
由题可知该几何体是三棱柱,它有两个底面,是三角形,三个侧面,是四边形,因此选项A,B,C均不符合题意,选项D符合题意.
2.A [解析]
柱体分为圆柱和棱柱,所以图中的柱体有圆柱、正方体、长方体、五棱柱和六棱柱,共5个.
3.球、圆柱
4.A
5.经过两点有一条直线,并且只有一条直线
6.E 两点之间的所有连线中,线段最短
7.D
8.D
9.56.8 4 18
10.解:(1)因为AB=3
cm,
所以AK=BK=AB=×3=1.5(cm).
因为AD=AB,所以AD=×3=1.5(cm).
设BC=x
cm,则AC=3x
cm,
由题意得3x=3+x,
解得x=1.5,即BC=1.5
cm,
所以DC=AD+AB+BC=1.5+3+1.5=6(cm).
(2)因为AK=BK,所以K是线段AB的中点.
又因为AD=BC,
所以AK+AD=BK+BC,即DK=CK,
所以K为线段DC的中点.
故K是线段AB和DC的中点.
11.解:因为∠AOB=110°,∠COD=70°,
所以∠AOC+∠BOD=∠AOB-∠COD=110°-70°=40°.
因为OA平分∠EOC,OB平分∠DOF,
所以∠AOE=∠AOC,∠BOF=∠BOD,
所以∠AOE+∠BOF=40°,
所以∠EOF=∠AOB+∠AOE+∠BOF=110°+40°=150°.
12.解:设∠BOC=2x°,
则∠AOE=5x°,∠AOD=8x°.
因为O是直线AB上一点,
所以∠AOB=180°,所以∠COE=(180-7x)°.
因为OE平分∠AOC,所以∠AOE=∠COE,
即180-7x=5x,解得x=15.
所以∠AOD=8×15°=120°,
所以∠BOD=60°.
13.B [解析]
因为一个角的补角是130°,所以这个角为50°,所以这个角的余角的度数是40°.
14.B
15.60°
16.B [解析]
将方格纸中的图形绕点O顺时针旋转90°后得到的图形如图所示.
17.解:如图,三角形A'B'C'即为所求.
18.10.4
cm [解析]
因为AD=AC,
所以DC=AC.
因为C是线段AB的中点,
所以AC=AB.
所以DC=×AB=AB.
因为CE=DE-DC,
所以CE=AB-AB=×24=10.4(cm).
故答案为10.4
cm.
19.解:(1)①∠COD=∠BOE.
理由:因为∠BOC=∠DOE=90°,
所以∠BOC+∠BOD=∠DOE+∠BOD,
即∠COD=∠BOE.
②∠BOD+∠COE=180°.
理由:因为∠DOE=90°,∠AOE+∠DOE+∠BOD=∠AOB=180°,
所以∠AOE+∠BOD=180°-90°=90°.
因为∠BOC=90°,所以∠AOC=90°,所以∠BOD+∠COE=∠BOD+∠AOE+∠AOC=90°+90°=180°.
(2)①因为∠BOC=∠COD+∠BOD=90°,∠DOE=∠BOD+∠BOE=90°,
所以∠COD=∠BOE.
②因为∠BOC=∠DOE=90°,
所以∠BOD+∠COE=∠BOD+∠COD+∠BOE+∠BOD=∠BOC+∠DOE=90°+90°=180°,
因此(1)②中的∠BOD和∠COE的关系还成立.
第二章 几何图形的初步认识
类型之一 立体图形的识别与分类
1.对如图1所示的几何体的认识正确的是
( )
图1
A.该棱柱的底面是四边形
B.该棱柱有四个面
C.该几何体是四棱柱
D.该棱柱的底面是三角形
2.下列几何体中,属于柱体的有
( )
图2
A.5个
B.4个
C.3个
D.2个
3.下列几何体中,含有曲面的是 .(填名称)?
图3
类型之二 用数学知识解释现实生活中的实际问题
4.雨滴滴下来形成雨丝,这一现象说明
( )
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
5.如图4,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线.能解释这一实际应用的数学知识是 .?
图4
6.如图5所示,在一条笔直公路l的两侧,分别有A,B两个小区,为了方便居民出行,现要在公路l上建一个公共自行车存放点,使存放点到A,B两个小区的距离之和最小,你认为存放点应该建在 处(填“C”“E”或“D”),理由是 .?
图5
类型之三 线段和角的计算
7.如图6所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是
( )
图6
A.20°
B.25°
C.30°
D.70°
8.如图7,已知M是线段AB的中点,N是线段AM上的点,且满足AN∶MN=1∶2.若AN=2
cm,则AB的长度是
( )
图7
A.6
cm
B.8
cm
C.10
cm
D.12
cm
9.56°48'= °,4.3°= ° '.?
10.如图8,已知线段AB=3
cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线上取一点D,使AD=AB.
(1)求线段BC,DC的长;
(2)K是哪些线段的中点?
图8
11.如图9,∠AOB=110°,∠COD=70°,OA平分∠EOC,OB平分∠DOF,求∠EOF的度数.
图9
12.如图10,O是直线AB上一点,OC,OD是从点O引出的两条射线,OE平分∠AOC,∠BOC∶∠AOE∶∠AOD=2∶5∶8,求∠BOD的度数.
图10
类型之四 余角和补角
13.如果一个角的补角是130°,那么这个角的余角的度数是
( )
A.30°
B.40°
C.50°
D.90°
14.如图11,已知∠AOC=∠BOC=90°,若∠1=∠2,则图中互余的角共有
( )
图11
A.5对
B.4对
C.3对
D.2对
15.若两个互补的角的度数之比为1∶2,则这两个角中较小的角的度数是 .?
图12
类型之五 图形的旋转
16.如图12,将方格纸中的图形绕点O顺时针旋转90°后得到的图形是
( )
图13
17.如图14,已知三角形ABC,请画出它绕点O顺时针旋转90°后得到的图形.
图14
18.[2020·晋州期中]
如图15,C是AB的中点,D,E分别是线段AC,CB上的点,AD=AC,DE=AB,若AB=24
cm,则线段CE的长为 .?
图15
19.[2020·遵化期中]
如图16,已知O为直线AB上的一点,∠BOC=∠DOE=90°.
(1)如图(a),当射线OC,OD在直线AB的两侧时,请回答下列问题,并说明理由.
①∠COD和∠BOE相等吗?
②∠BOD和∠COE有什么数量关系?
(2)如图(b),当射线OC,OD在直线AB的同侧时,请直接回答下列问题.
①∠COD和∠BOE相等吗?
②(1)②中的∠BOD和∠COE的关系还成立吗?
(a) (b)
图16
答案
1.D [解析]
由题可知该几何体是三棱柱,它有两个底面,是三角形,三个侧面,是四边形,因此选项A,B,C均不符合题意,选项D符合题意.
2.A [解析]
柱体分为圆柱和棱柱,所以图中的柱体有圆柱、正方体、长方体、五棱柱和六棱柱,共5个.
3.球、圆柱
4.A
5.经过两点有一条直线,并且只有一条直线
6.E 两点之间的所有连线中,线段最短
7.D
8.D
9.56.8 4 18
10.解:(1)因为AB=3
cm,
所以AK=BK=AB=×3=1.5(cm).
因为AD=AB,所以AD=×3=1.5(cm).
设BC=x
cm,则AC=3x
cm,
由题意得3x=3+x,
解得x=1.5,即BC=1.5
cm,
所以DC=AD+AB+BC=1.5+3+1.5=6(cm).
(2)因为AK=BK,所以K是线段AB的中点.
又因为AD=BC,
所以AK+AD=BK+BC,即DK=CK,
所以K为线段DC的中点.
故K是线段AB和DC的中点.
11.解:因为∠AOB=110°,∠COD=70°,
所以∠AOC+∠BOD=∠AOB-∠COD=110°-70°=40°.
因为OA平分∠EOC,OB平分∠DOF,
所以∠AOE=∠AOC,∠BOF=∠BOD,
所以∠AOE+∠BOF=40°,
所以∠EOF=∠AOB+∠AOE+∠BOF=110°+40°=150°.
12.解:设∠BOC=2x°,
则∠AOE=5x°,∠AOD=8x°.
因为O是直线AB上一点,
所以∠AOB=180°,所以∠COE=(180-7x)°.
因为OE平分∠AOC,所以∠AOE=∠COE,
即180-7x=5x,解得x=15.
所以∠AOD=8×15°=120°,
所以∠BOD=60°.
13.B [解析]
因为一个角的补角是130°,所以这个角为50°,所以这个角的余角的度数是40°.
14.B
15.60°
16.B [解析]
将方格纸中的图形绕点O顺时针旋转90°后得到的图形如图所示.
17.解:如图,三角形A'B'C'即为所求.
18.10.4
cm [解析]
因为AD=AC,
所以DC=AC.
因为C是线段AB的中点,
所以AC=AB.
所以DC=×AB=AB.
因为CE=DE-DC,
所以CE=AB-AB=×24=10.4(cm).
故答案为10.4
cm.
19.解:(1)①∠COD=∠BOE.
理由:因为∠BOC=∠DOE=90°,
所以∠BOC+∠BOD=∠DOE+∠BOD,
即∠COD=∠BOE.
②∠BOD+∠COE=180°.
理由:因为∠DOE=90°,∠AOE+∠DOE+∠BOD=∠AOB=180°,
所以∠AOE+∠BOD=180°-90°=90°.
因为∠BOC=90°,所以∠AOC=90°,所以∠BOD+∠COE=∠BOD+∠AOE+∠AOC=90°+90°=180°.
(2)①因为∠BOC=∠COD+∠BOD=90°,∠DOE=∠BOD+∠BOE=90°,
所以∠COD=∠BOE.
②因为∠BOC=∠DOE=90°,
所以∠BOD+∠COE=∠BOD+∠COD+∠BOE+∠BOD=∠BOC+∠DOE=90°+90°=180°,
因此(1)②中的∠BOD和∠COE的关系还成立.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
