冀教版八年级数学上册 第十三章 全等三角形练习题 (word版,含答案)
文档属性
| 名称 | 冀教版八年级数学上册 第十三章 全等三角形练习题 (word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 11:56:41 | ||
图片预览



文档简介
第十三章
全等三角形
类型一 命题与证明
1.下列命题中,其逆命题是真命题的是
( )
A.若a>1且b>1,则a+b>2
B.若ab=1,则a与b互为倒数
C.全等三角形的三个角对应相等
D.全等三角形的面积相等
类型二 全等三角形的判定
2.如图1,已知CD⊥AB于点D,点E在CD上,现有四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④CD=BD.其中不能得出△ADC≌△EDB的条件是
( )
图1
A.①③
B.②④
C.①④
D.②③
3.如图2,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是 .(只填一个即可)?
图2
4.如图3,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
图3
类型三 全等三角形的判定与性质的综合
5.如图4,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是
( )
图4
A.0.5
B.1
C.1.5
D.2
6.如图5,在△ABC中,D,E,F分别是BC,AB,AC上的点.若∠B=∠C,BE=CD,BD=CF,∠EDF=54°,则∠A的度数为
( )
图5
A.54°
B.72°
C.80°
D.108°
7.如图6,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
图6
8.如图7,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
图7
类型四 尺规作图
9.已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法的合理顺序为 .(填序号)?
①分别以点B,C为圆心,c,b为半径作弧,两弧交于点A;
②作射线BP,在射线BP上截取BC=a;
③连接AB,AC,△ABC为所求作的三角形(如图8).
图8
10.已知∠AOB=60°,以点O为圆心,以任意长为半径作弧,分别交OA,OB于点M,N;分别以点M,N为圆心,以大于MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为
( )
A.15°
B.45°
C.15°或30°
D.15°或45°
11.如图9,AC,BD相交于点E,AB=DC,AC=DB,则图中有全等三角形
( )
图9
A.1对
B.2对
C.3对
D.4对
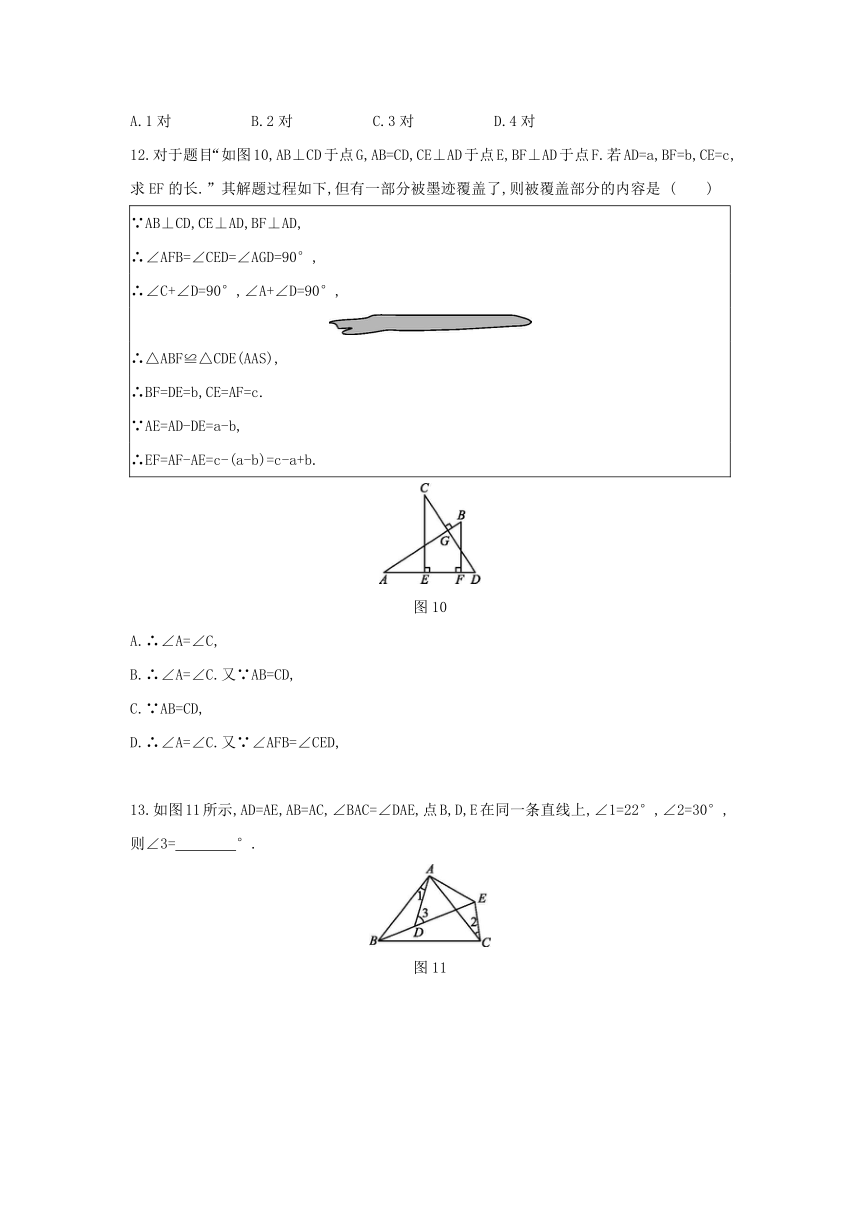
12.对于题目“如图10,AB⊥CD于点G,AB=CD,CE⊥AD于点E,BF⊥AD于点F.若AD=a,BF=b,CE=c,求EF的长.”其解题过程如下,但有一部分被墨迹覆盖了,则被覆盖部分的内容是
( )
∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=∠AGD=90°,
∴∠C+∠D=90°,∠A+∠D=90°,
∴△ABF≌△CDE(AAS),
∴BF=DE=b,CE=AF=c.
∵AE=AD-DE=a-b,
∴EF=AF-AE=c-(a-b)=c-a+b.
图10
A.∴∠A=∠C,
B.∴∠A=∠C.又∵AB=CD,
C.∵AB=CD,
D.∴∠A=∠C.又∵∠AFB=∠CED,
13.如图11所示,AD=AE,AB=AC,∠BAC=∠DAE,点B,D,E在同一条直线上,∠1=22°,∠2=30°,则∠3= °.?
图11
14.如图12,王强同学用10块高度都是2
cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和点B分别与木墙的顶端重合,求两堵木墙之间的距离.
图12
答案
1.B [解析]
A.逆命题是“若a+b>2,则a>1且b>1”,是假命题;B.逆命题是“若a与b互为倒数,则ab=1”,是真命题;C.逆命题是“三个角对应相等的三角形是全等三角形”,是假命题;D.逆命题是“面积相等的三角形全等”,是假命题.
2.D [解析]
A项,∵CD⊥AB,
∴∠ADC=∠EDB=90°.
在△ADC和△EDB中,∵
∴△ADC≌△EDB(AAS),故本选项不符合题意;
B项,∵CD⊥AB,∴∠ADC=∠EDB=90°.
在△ADC和△EDB中,∵
∴△ADC≌△EDB(AAS),故本选项不符合题意;
C项,∵CD⊥AB,∴∠ADC=∠EDB=90°.
在△ADC和△EDB中,∵
∴△ADC≌△EDB(SAS),故本选项不符合题意;
D项,根据三个角对应相等,不能判定两个三角形全等,故本选项符合题意.故选D.
3.答案不唯一,如AD=AC或∠D=∠C或∠ABD=∠ABC等 [解析]
∵∠DAB=∠CAB,AB=AB,∴当添加AD=AC时,可根据“SAS”判定△ABD≌△ABC;当添加∠D=∠C时,可根据“AAS”判定△ABD≌△ABC;当添加∠ABD=∠ABC时,可根据“ASA”判定△ABD≌△ABC.
4.证明:∵DE∥AC,∴∠EDB=∠A.
在△DEB和△ABC中,∵
∴△DEB≌△ABC(SAS).
5.B [解析]
∵FC∥AB,
∴∠A=∠FCE,∠ADE=∠F.
在△ADE和△CFE中,∵
∴△ADE≌△CFE(AAS),∴AD=CF=3.
∵AB=4,∴BD=AB-AD=4-3=1.
6.B [解析]
在△BDE和△CFD中,∵
∴△BDE≌△CFD(SAS),
∴∠BED=∠CDF,
∴∠BED+∠BDE=∠CDF+∠BDE.
∵∠BED+∠BDE+∠B=∠CDF+∠BDE+∠EDF=180°,∴∠B=∠EDF=54°,
∴∠A=180°-∠B-∠C=72°.
7.解:(1)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是BC边上的中线,∴BD=CD.
在△BDE和△CDF中,∵
∴△BDE≌△CDF(AAS).
(2)∵△BDE≌△CDF,∴BE=CF=2,
∴AB=AE+BE=1+2=3.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
在△ADB和△ADC中,∵
∴△ADB≌△ADC,∴AC=AB=3.
8.解:(1)证明:在△BEF和△CDA中,∵
∴△BEF≌△CDA(SAS),∴∠D=∠2.
(2)∵∠D=∠2,∠D=78°,∴∠2=78°.
∵EF∥AC,∴∠BAC=∠2=78°.
9.②①③
10.D [解析]
以点O为圆心,以任意长为半径画弧,分别交OA,OB于点M,N;分别以点M,N为圆心,以大于MN的长度为半径画弧,两弧在∠AOB内交于点P,由两个三角形全等可知,OP为∠AOB的平分线,如图.
以OP为边作∠POC=15°,则射线OC可能在∠POB的内部,也可能在∠POB的外部.
由∠AOB=60°,可得∠POB=30°.
当射线OC在∠POB的内部时,∠BOC=15°;
当射线OC'在∠POB的外部时,∠BOC'=45°.故选D.
11.C [解析]
∵AB=DC,AC=DB,又∵BC=CB,∴△ABC≌△DCB(SSS);又∵AD=DA,∴△ABD≌△DCA(SSS),∴∠BAC=∠CDB;又∵AB=CD,∠AEB=∠DEC,∴△ABE≌△DCE(AAS).
故选C.
12.B [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠AFB=∠CED=∠AGD=90°,∴∠C+∠D=90°,∠A+∠D=90°,∴∠A=∠C.又∵AB=CD,∠AFB=∠CED,∴△ABF≌△CDE(AAS),∴BF=DE=b,CE=AF=c.∵AE=AD-DE=a-b,∴EF=AF-AE=c-(a-b)=c-a+b.故选B.
13.52 [解析]
∵∠BAC=∠DAE,
∴∠1=∠CAE.
在△ABD和△ACE中,∵
∴△ABD≌△ACE(SAS),
∴∠ABD=∠2=30°,
∴∠3=∠1+∠ABD=52°.
14.解:由题意,得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC.
在△ADC和△CEB中,∵
∴△ADC≌△CEB(AAS),
∴AD=CE=6
cm,DC=EB=14
cm,
∴DE=DC+CE=14+6=20(cm).
故两堵木墙之间的距离为20
cm.
全等三角形
类型一 命题与证明
1.下列命题中,其逆命题是真命题的是
( )
A.若a>1且b>1,则a+b>2
B.若ab=1,则a与b互为倒数
C.全等三角形的三个角对应相等
D.全等三角形的面积相等
类型二 全等三角形的判定
2.如图1,已知CD⊥AB于点D,点E在CD上,现有四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④CD=BD.其中不能得出△ADC≌△EDB的条件是
( )
图1
A.①③
B.②④
C.①④
D.②③
3.如图2,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是 .(只填一个即可)?
图2
4.如图3,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
图3
类型三 全等三角形的判定与性质的综合
5.如图4,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是
( )
图4
A.0.5
B.1
C.1.5
D.2
6.如图5,在△ABC中,D,E,F分别是BC,AB,AC上的点.若∠B=∠C,BE=CD,BD=CF,∠EDF=54°,则∠A的度数为
( )
图5
A.54°
B.72°
C.80°
D.108°
7.如图6,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
图6
8.如图7,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
图7
类型四 尺规作图
9.已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法的合理顺序为 .(填序号)?
①分别以点B,C为圆心,c,b为半径作弧,两弧交于点A;
②作射线BP,在射线BP上截取BC=a;
③连接AB,AC,△ABC为所求作的三角形(如图8).
图8
10.已知∠AOB=60°,以点O为圆心,以任意长为半径作弧,分别交OA,OB于点M,N;分别以点M,N为圆心,以大于MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为
( )
A.15°
B.45°
C.15°或30°
D.15°或45°
11.如图9,AC,BD相交于点E,AB=DC,AC=DB,则图中有全等三角形
( )
图9
A.1对
B.2对
C.3对
D.4对
12.对于题目“如图10,AB⊥CD于点G,AB=CD,CE⊥AD于点E,BF⊥AD于点F.若AD=a,BF=b,CE=c,求EF的长.”其解题过程如下,但有一部分被墨迹覆盖了,则被覆盖部分的内容是
( )
∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=∠AGD=90°,
∴∠C+∠D=90°,∠A+∠D=90°,
∴△ABF≌△CDE(AAS),
∴BF=DE=b,CE=AF=c.
∵AE=AD-DE=a-b,
∴EF=AF-AE=c-(a-b)=c-a+b.
图10
A.∴∠A=∠C,
B.∴∠A=∠C.又∵AB=CD,
C.∵AB=CD,
D.∴∠A=∠C.又∵∠AFB=∠CED,
13.如图11所示,AD=AE,AB=AC,∠BAC=∠DAE,点B,D,E在同一条直线上,∠1=22°,∠2=30°,则∠3= °.?
图11
14.如图12,王强同学用10块高度都是2
cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和点B分别与木墙的顶端重合,求两堵木墙之间的距离.
图12
答案
1.B [解析]
A.逆命题是“若a+b>2,则a>1且b>1”,是假命题;B.逆命题是“若a与b互为倒数,则ab=1”,是真命题;C.逆命题是“三个角对应相等的三角形是全等三角形”,是假命题;D.逆命题是“面积相等的三角形全等”,是假命题.
2.D [解析]
A项,∵CD⊥AB,
∴∠ADC=∠EDB=90°.
在△ADC和△EDB中,∵
∴△ADC≌△EDB(AAS),故本选项不符合题意;
B项,∵CD⊥AB,∴∠ADC=∠EDB=90°.
在△ADC和△EDB中,∵
∴△ADC≌△EDB(AAS),故本选项不符合题意;
C项,∵CD⊥AB,∴∠ADC=∠EDB=90°.
在△ADC和△EDB中,∵
∴△ADC≌△EDB(SAS),故本选项不符合题意;
D项,根据三个角对应相等,不能判定两个三角形全等,故本选项符合题意.故选D.
3.答案不唯一,如AD=AC或∠D=∠C或∠ABD=∠ABC等 [解析]
∵∠DAB=∠CAB,AB=AB,∴当添加AD=AC时,可根据“SAS”判定△ABD≌△ABC;当添加∠D=∠C时,可根据“AAS”判定△ABD≌△ABC;当添加∠ABD=∠ABC时,可根据“ASA”判定△ABD≌△ABC.
4.证明:∵DE∥AC,∴∠EDB=∠A.
在△DEB和△ABC中,∵
∴△DEB≌△ABC(SAS).
5.B [解析]
∵FC∥AB,
∴∠A=∠FCE,∠ADE=∠F.
在△ADE和△CFE中,∵
∴△ADE≌△CFE(AAS),∴AD=CF=3.
∵AB=4,∴BD=AB-AD=4-3=1.
6.B [解析]
在△BDE和△CFD中,∵
∴△BDE≌△CFD(SAS),
∴∠BED=∠CDF,
∴∠BED+∠BDE=∠CDF+∠BDE.
∵∠BED+∠BDE+∠B=∠CDF+∠BDE+∠EDF=180°,∴∠B=∠EDF=54°,
∴∠A=180°-∠B-∠C=72°.
7.解:(1)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F.
∵AD是BC边上的中线,∴BD=CD.
在△BDE和△CDF中,∵
∴△BDE≌△CDF(AAS).
(2)∵△BDE≌△CDF,∴BE=CF=2,
∴AB=AE+BE=1+2=3.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
在△ADB和△ADC中,∵
∴△ADB≌△ADC,∴AC=AB=3.
8.解:(1)证明:在△BEF和△CDA中,∵
∴△BEF≌△CDA(SAS),∴∠D=∠2.
(2)∵∠D=∠2,∠D=78°,∴∠2=78°.
∵EF∥AC,∴∠BAC=∠2=78°.
9.②①③
10.D [解析]
以点O为圆心,以任意长为半径画弧,分别交OA,OB于点M,N;分别以点M,N为圆心,以大于MN的长度为半径画弧,两弧在∠AOB内交于点P,由两个三角形全等可知,OP为∠AOB的平分线,如图.
以OP为边作∠POC=15°,则射线OC可能在∠POB的内部,也可能在∠POB的外部.
由∠AOB=60°,可得∠POB=30°.
当射线OC在∠POB的内部时,∠BOC=15°;
当射线OC'在∠POB的外部时,∠BOC'=45°.故选D.
11.C [解析]
∵AB=DC,AC=DB,又∵BC=CB,∴△ABC≌△DCB(SSS);又∵AD=DA,∴△ABD≌△DCA(SSS),∴∠BAC=∠CDB;又∵AB=CD,∠AEB=∠DEC,∴△ABE≌△DCE(AAS).
故选C.
12.B [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠AFB=∠CED=∠AGD=90°,∴∠C+∠D=90°,∠A+∠D=90°,∴∠A=∠C.又∵AB=CD,∠AFB=∠CED,∴△ABF≌△CDE(AAS),∴BF=DE=b,CE=AF=c.∵AE=AD-DE=a-b,∴EF=AF-AE=c-(a-b)=c-a+b.故选B.
13.52 [解析]
∵∠BAC=∠DAE,
∴∠1=∠CAE.
在△ABD和△ACE中,∵
∴△ABD≌△ACE(SAS),
∴∠ABD=∠2=30°,
∴∠3=∠1+∠ABD=52°.
14.解:由题意,得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC.
在△ADC和△CEB中,∵
∴△ADC≌△CEB(AAS),
∴AD=CE=6
cm,DC=EB=14
cm,
∴DE=DC+CE=14+6=20(cm).
故两堵木墙之间的距离为20
cm.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
