2021-2022学年冀教版九年级数学上册23.4 用样本估计总体课时训练卷(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册23.4 用样本估计总体课时训练卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 272.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览


文档简介
冀教版九年级数学上册
23.4
用样本估计总体
课时训练卷
一、选择题(共8小题,4
8=32)
1.一组数据经过整理后的结果如下表:则这组数据的平均数是(
)
分组
0≤x<10
10≤x<20
频数
8
12
A.10
B.11
C.12
D.16
2.抽查某单位6月份5天的日用水量,结果(单位:吨)如下:15,14,17,12,7,根据这些数据,估计该单位6月份总用水量为(
)
A.360吨
B.384吨
C.390吨
D.415吨
3.为了解某校九年级学生每天的睡眠时间情况,随机调查了该校九年级20名学生,将所得数据整理并制成下表:
睡眠时间(小时)
6
7
8
9
学生人数
8
6
4
2
据此估计该校九年级学生每天的平均睡眠时间大约是(
)
A.7小时
B.7.2小时
C.8小时
D.8.3小时
4.有4万个不小于70的两位数,从中随机抽取3
000个数据,统计如下:
数据x
70≤x≤79
80≤x≤89
90≤x≤99
个数
800
1
300
900
平均数
78.1
85
91.9
请根据表格中的信息,估计这4万个数据的平均数为( )
A.92.16
B.85.23
C.84.73
D.77.97
5.为了从甲、乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同的条件下各射靶10次,为了比较两人的成绩,制作了如下统计表:
平均数
中位数
方差
命中10环的次数
甲
9.5
9.5
3.7
1
乙
9.5
9.6
5.4
2
若想选拔一位成绩稳定的选手参赛,则表中几个数据应该重点关注的是( )
A.中位数
B.平均数
C.方差
D.命中10环的次数
6.
去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差s2(单位:千克2)如表所示:
甲
乙
丙
丁
x
24
24
23
20
s2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是(
)
A.甲
B.乙
C.丙
D.丁
7.市运会举行射击比赛,某校射击队从甲、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每人射击10次,计算他们10次成绩的平均数(环)及方差如下表,
?
甲
乙
丙
丁
平均数
8.2
8.0
8.2
8.0
方差
2.0
1.8
1.5
1.6
请你根据表中数据选一人参加比赛,最合适的人选是(
)
A.
甲
B.
乙
C.
丙
D.
丁
8.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是x甲=610千克,x乙=608千克,亩产量的方差分别为s甲2=29.6,s乙2=2.7,则关于两种小麦推广种植的合理决策是(
)
A.甲的平均亩产量较高,应推广甲
B.甲、乙的平均亩产量相差不多,均可推广
C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
二.填空题(共6小题,4
6=24)
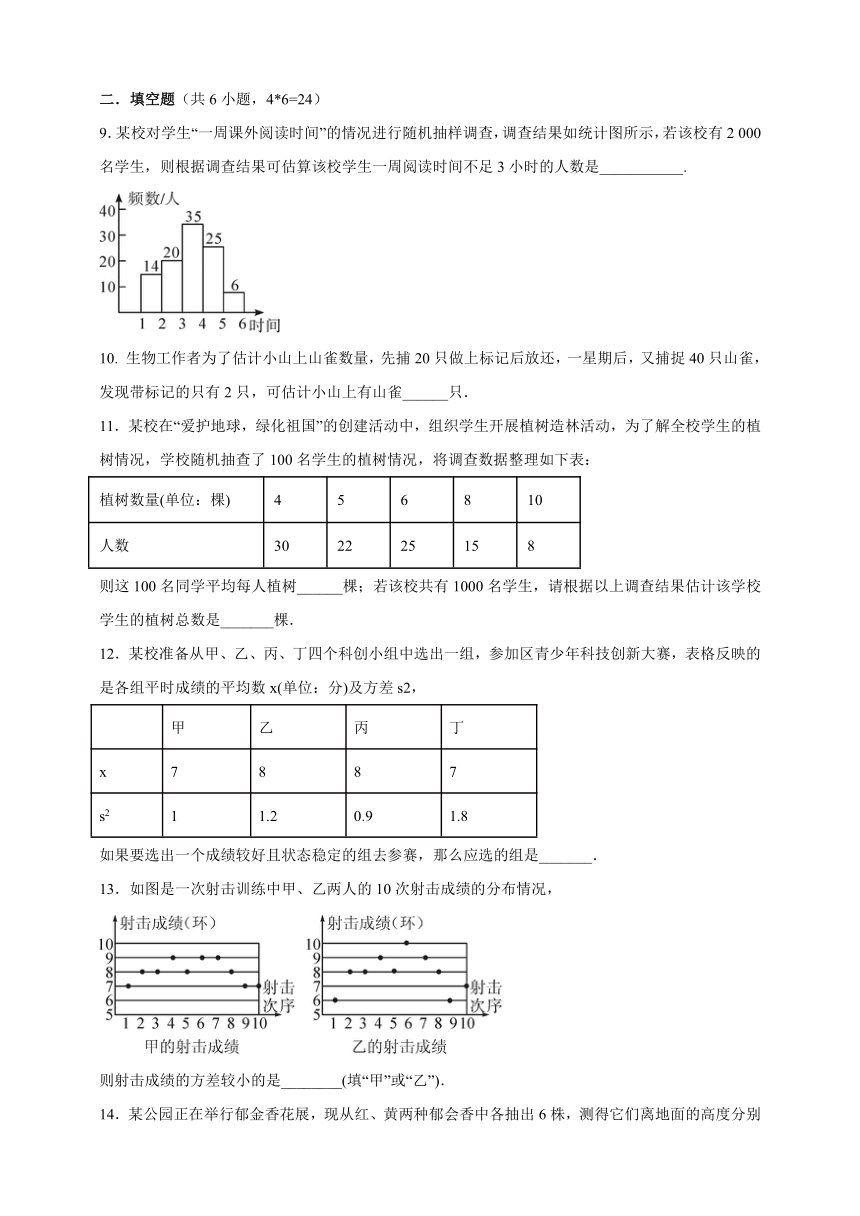
9.某校对学生“一周课外阅读时间”的情况进行随机抽样调查,调查结果如统计图所示,若该校有2
000名学生,则根据调查结果可估算该校学生一周阅读时间不足3小时的人数是___________.
10.
生物工作者为了估计小山上山雀数量,先捕20只做上标记后放还,一星期后,又捕捉40只山雀,发现带标记的只有2只,可估计小山上有山雀______只.
11.某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动,为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵)
4
5
6
8
10
人数
30
22
25
15
8
则这100名同学平均每人植树______棵;若该校共有1000名学生,请根据以上调查结果估计该学校学生的植树总数是_______棵.
12.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数x(单位:分)及方差s2,
甲
乙
丙
丁
x
7
8
8
7
s2
1
1.2
0.9
1.8
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是_______.
13.如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况,
则射击成绩的方差较小的是________(填“甲”或“乙”).
14.某公园正在举行郁金香花展,现从红、黄两种郁会香中各抽出6株,测得它们离地面的高度分别如下(单位:cm):
红:54,44,37,36,35,34;
黄:48,35,38,36,43,40;
已知它们的平均高度均是40
cm,请判断哪种颜色的郁金香样本长得整齐?_______(填“红”或“黄”).
三.解答题(共6小题,
44分)
15.(6分)
在某次慈善一日捐活动中,学校团总支为了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)求这50名同学捐款的平均数;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
16.(8分)
下表是八(2)班30名学生期中测试物理成绩表(已污损):
已知该班期中测试物理成绩的平均分是76分,该班得80分和90分的各有多少人?
17.(8分)
王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已结果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明哪个山上的杨梅产量较稳定.
18.(10分)
为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表:(单位:秒)
类型编号
一
二
三
四
五
六
七
八
九
十
甲种电子钟
1
-3
-4
4
2
-2
2
-1
-1
2
乙种电子钟
4
-3
-1
2
-2
1
-2
2
-2
1
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
19.(12分)
我市民营经济持续发展,2020年城镇民营企业就业人数突破20万.为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2020年月平均收入随机抽样调查,将抽样的数据按“2
000元以内”“2
000~4
000元”“4
000~6
000元”和“6
000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下面两幅不完整的统计图.
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有多少人?在扇形统计图中x的值为多少?表示“月平均收入在2
000元以内”的部分所对应扇形的圆心角的度数是多少度?
(2)将不完整的条形统计图补充完整,并估计我市2020年城镇民营企业20万员工中,每月的收入在“2
000~4
000元”的约有多少人?
(3)统计局根据抽样数据计算得到,2020年我市城镇民营企业员工月平均收入为4
872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
参考答案
1-4
BCAB
5-8CBCD
9.
680人
10.
400
11.
5.8,5800
12.
丙
13.
甲
14.
黄
15.
解:(1)(5×8+10×14+15×20+20×6+25×2)÷50=13(元)
(2)600×13=7800(元)
16.
解:设该班得80分的有x人,得90分的有y人,由题意得解得则该班得80分的有8人,得90分的有5人
17.
解:(1)x甲=40,x乙=40,总产量为40×100×98%×2=7840(千克)
(2)s甲2=[(50-40)2+(36-40)2+(40-40)2+(34-40)2]=38,
s乙2=[(36-40)2+(40-40)2+(48-40)2+(36-40)2]=24,s甲2>s乙2,∴乙山上的杨梅产量较稳定
18.
解:(1)甲种电子钟走时误差的平均数为:
×(1-3-4+4+2-2+2-1-1+2)=0,乙种电子钟走时误差的平均数为:
×(4-3-1+2-2+1-2+2-2+1)=0,∴两种电子钟走时误差的平均数都是0秒
(2)s甲2=6,s乙2=4.8.
(3)我会买乙种电子钟,因平均水平相同,但甲的方差比乙的方差大,说明乙的稳定性更好,故乙种电子钟质量更优
19.
解:(1)本次抽样调查的人数是300÷60%=500,x=100×=14,表示“月平均收入在2
000元以内”的部分所对应扇形的圆心角的度数是360°×=21.6°.
(2)C组的人数是500-30-300-70=100,
补全条形统计图如图所示.
估计我市2020年城镇民营企业20万员工中,每月的收入在“2
000~4
000元”的约有20×=12(万人).
(3)不合理,因为平均数不能代表大多数人的收入,应该用中位数或众数代表.
23.4
用样本估计总体
课时训练卷
一、选择题(共8小题,4
8=32)
1.一组数据经过整理后的结果如下表:则这组数据的平均数是(
)
分组
0≤x<10
10≤x<20
频数
8
12
A.10
B.11
C.12
D.16
2.抽查某单位6月份5天的日用水量,结果(单位:吨)如下:15,14,17,12,7,根据这些数据,估计该单位6月份总用水量为(
)
A.360吨
B.384吨
C.390吨
D.415吨
3.为了解某校九年级学生每天的睡眠时间情况,随机调查了该校九年级20名学生,将所得数据整理并制成下表:
睡眠时间(小时)
6
7
8
9
学生人数
8
6
4
2
据此估计该校九年级学生每天的平均睡眠时间大约是(
)
A.7小时
B.7.2小时
C.8小时
D.8.3小时
4.有4万个不小于70的两位数,从中随机抽取3
000个数据,统计如下:
数据x
70≤x≤79
80≤x≤89
90≤x≤99
个数
800
1
300
900
平均数
78.1
85
91.9
请根据表格中的信息,估计这4万个数据的平均数为( )
A.92.16
B.85.23
C.84.73
D.77.97
5.为了从甲、乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同的条件下各射靶10次,为了比较两人的成绩,制作了如下统计表:
平均数
中位数
方差
命中10环的次数
甲
9.5
9.5
3.7
1
乙
9.5
9.6
5.4
2
若想选拔一位成绩稳定的选手参赛,则表中几个数据应该重点关注的是( )
A.中位数
B.平均数
C.方差
D.命中10环的次数
6.
去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差s2(单位:千克2)如表所示:
甲
乙
丙
丁
x
24
24
23
20
s2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是(
)
A.甲
B.乙
C.丙
D.丁
7.市运会举行射击比赛,某校射击队从甲、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每人射击10次,计算他们10次成绩的平均数(环)及方差如下表,
?
甲
乙
丙
丁
平均数
8.2
8.0
8.2
8.0
方差
2.0
1.8
1.5
1.6
请你根据表中数据选一人参加比赛,最合适的人选是(
)
A.
甲
B.
乙
C.
丙
D.
丁
8.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是x甲=610千克,x乙=608千克,亩产量的方差分别为s甲2=29.6,s乙2=2.7,则关于两种小麦推广种植的合理决策是(
)
A.甲的平均亩产量较高,应推广甲
B.甲、乙的平均亩产量相差不多,均可推广
C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
二.填空题(共6小题,4
6=24)
9.某校对学生“一周课外阅读时间”的情况进行随机抽样调查,调查结果如统计图所示,若该校有2
000名学生,则根据调查结果可估算该校学生一周阅读时间不足3小时的人数是___________.
10.
生物工作者为了估计小山上山雀数量,先捕20只做上标记后放还,一星期后,又捕捉40只山雀,发现带标记的只有2只,可估计小山上有山雀______只.
11.某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动,为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵)
4
5
6
8
10
人数
30
22
25
15
8
则这100名同学平均每人植树______棵;若该校共有1000名学生,请根据以上调查结果估计该学校学生的植树总数是_______棵.
12.某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数x(单位:分)及方差s2,
甲
乙
丙
丁
x
7
8
8
7
s2
1
1.2
0.9
1.8
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是_______.
13.如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况,
则射击成绩的方差较小的是________(填“甲”或“乙”).
14.某公园正在举行郁金香花展,现从红、黄两种郁会香中各抽出6株,测得它们离地面的高度分别如下(单位:cm):
红:54,44,37,36,35,34;
黄:48,35,38,36,43,40;
已知它们的平均高度均是40
cm,请判断哪种颜色的郁金香样本长得整齐?_______(填“红”或“黄”).
三.解答题(共6小题,
44分)
15.(6分)
在某次慈善一日捐活动中,学校团总支为了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)求这50名同学捐款的平均数;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
16.(8分)
下表是八(2)班30名学生期中测试物理成绩表(已污损):
已知该班期中测试物理成绩的平均分是76分,该班得80分和90分的各有多少人?
17.(8分)
王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已结果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明哪个山上的杨梅产量较稳定.
18.(10分)
为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表:(单位:秒)
类型编号
一
二
三
四
五
六
七
八
九
十
甲种电子钟
1
-3
-4
4
2
-2
2
-1
-1
2
乙种电子钟
4
-3
-1
2
-2
1
-2
2
-2
1
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
19.(12分)
我市民营经济持续发展,2020年城镇民营企业就业人数突破20万.为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2020年月平均收入随机抽样调查,将抽样的数据按“2
000元以内”“2
000~4
000元”“4
000~6
000元”和“6
000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下面两幅不完整的统计图.
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有多少人?在扇形统计图中x的值为多少?表示“月平均收入在2
000元以内”的部分所对应扇形的圆心角的度数是多少度?
(2)将不完整的条形统计图补充完整,并估计我市2020年城镇民营企业20万员工中,每月的收入在“2
000~4
000元”的约有多少人?
(3)统计局根据抽样数据计算得到,2020年我市城镇民营企业员工月平均收入为4
872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
参考答案
1-4
BCAB
5-8CBCD
9.
680人
10.
400
11.
5.8,5800
12.
丙
13.
甲
14.
黄
15.
解:(1)(5×8+10×14+15×20+20×6+25×2)÷50=13(元)
(2)600×13=7800(元)
16.
解:设该班得80分的有x人,得90分的有y人,由题意得解得则该班得80分的有8人,得90分的有5人
17.
解:(1)x甲=40,x乙=40,总产量为40×100×98%×2=7840(千克)
(2)s甲2=[(50-40)2+(36-40)2+(40-40)2+(34-40)2]=38,
s乙2=[(36-40)2+(40-40)2+(48-40)2+(36-40)2]=24,s甲2>s乙2,∴乙山上的杨梅产量较稳定
18.
解:(1)甲种电子钟走时误差的平均数为:
×(1-3-4+4+2-2+2-1-1+2)=0,乙种电子钟走时误差的平均数为:
×(4-3-1+2-2+1-2+2-2+1)=0,∴两种电子钟走时误差的平均数都是0秒
(2)s甲2=6,s乙2=4.8.
(3)我会买乙种电子钟,因平均水平相同,但甲的方差比乙的方差大,说明乙的稳定性更好,故乙种电子钟质量更优
19.
解:(1)本次抽样调查的人数是300÷60%=500,x=100×=14,表示“月平均收入在2
000元以内”的部分所对应扇形的圆心角的度数是360°×=21.6°.
(2)C组的人数是500-30-300-70=100,
补全条形统计图如图所示.
估计我市2020年城镇民营企业20万员工中,每月的收入在“2
000~4
000元”的约有20×=12(万人).
(3)不合理,因为平均数不能代表大多数人的收入,应该用中位数或众数代表.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
