25.4相似三角形的判定 同步提高训练(Word版 附答案) 2021-2022学年冀教版九年级数学上册
文档属性
| 名称 | 25.4相似三角形的判定 同步提高训练(Word版 附答案) 2021-2022学年冀教版九年级数学上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 199.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 12:49:22 | ||
图片预览




文档简介
2021-2022学年冀教版九年级数学上册《25.4相似三角形的判定》
同步能力提高训练(附答案)
一.选择题
1.如图,点D,E分别在△ABC的AB,AC边上,增加下列哪个条件不能使△ADE与△ABC相似?( )
A.=
B.=
C.∠AED=∠B
D.∠AED=∠C
2.下列命题是真命题的是( )
A.同旁内角相等,两直线平行
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.两角分别相等的两个三角形相似
3.下列可以判定△ABC∽△A'B'C'的条件是( )
A.∠A=∠B'=∠C'
B.=且∠A=∠C'
C.=且∠A=∠A'
D.以上条件都不对
4.如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,不能判定△APC与△ACB相似的是( )
A.①
B.②
C.③
D.④
5.下列条件中,能使△ABC∽△DEF成立的是( )
A.∠C=98°,∠E=98°,
B.AB=1,AC=1.5,BC=2,EF=8,DE=10,FD=6
C.∠A=∠F=90°,AC=5,BC=13,DF=10,EF=26
D.∠B=35°,BC=10,BC上的高AG=7,∠E=35°,EF=5,EF上的高DH=3.5
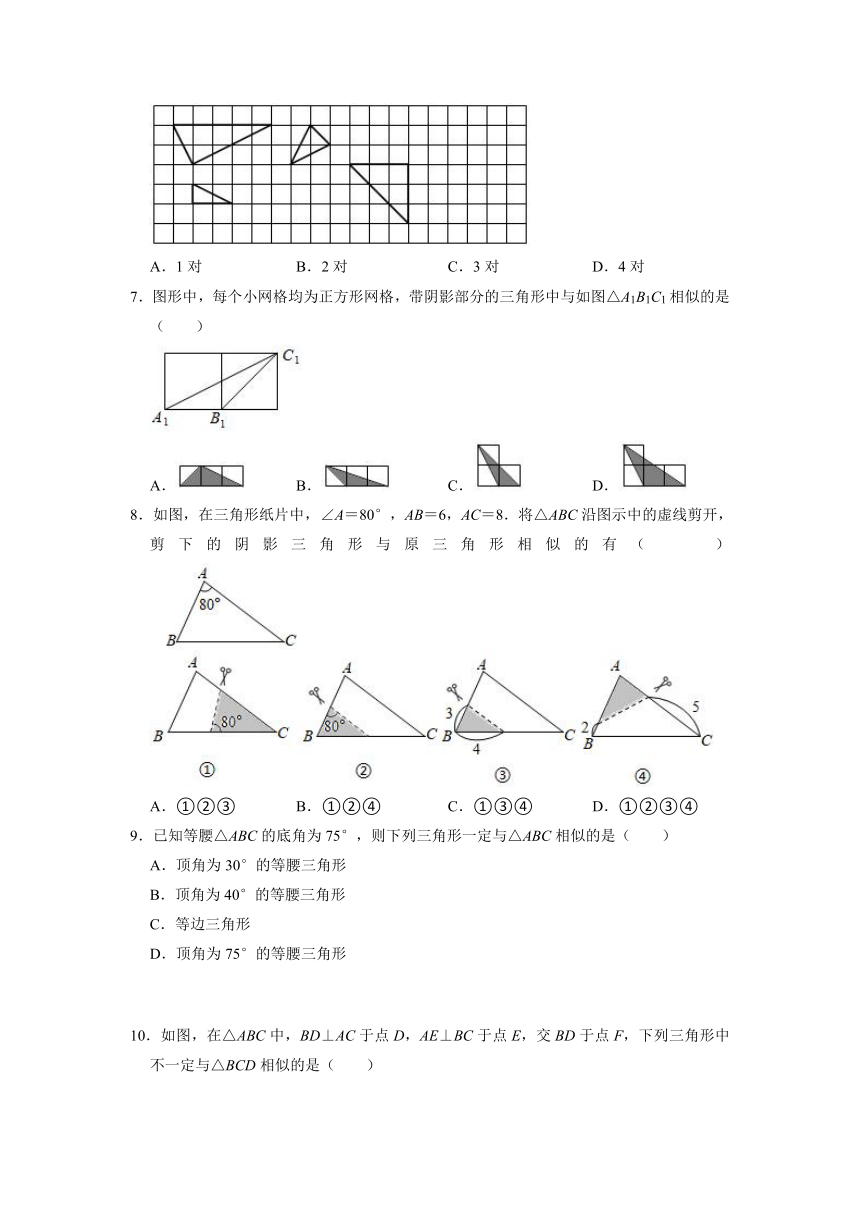
6.如图所示的4个三角形中,相似三角形有( )
A.1对
B.2对
C.3对
D.4对
7.图形中,每个小网格均为正方形网格,带阴影部分的三角形中与如图△A1B1C1相似的是( )
A.
B.
C.
D.
8.如图,在三角形纸片中,∠A=80°,AB=6,AC=8.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )
A.①②③
B.①②④
C.①③④
D.①②③④
9.已知等腰△ABC的底角为75°,则下列三角形一定与△ABC相似的是( )
A.顶角为30°的等腰三角形
B.顶角为40°的等腰三角形
C.等边三角形
D.顶角为75°的等腰三角形
10.如图,在△ABC中,BD⊥AC于点D,AE⊥BC于点E,交BD于点F,下列三角形中不一定与△BCD相似的是( )
A.△BFE
B.△AFD
C.△ACE
D.△BAE
二.解答题
11.如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△PBD.
12.如图,在矩形ABCD中,点E为BC上一点,连接DE,过点A作AF⊥DE于点F,求证:△DEC∽△ADF.
13.如图,点B,C分别在△ADE的边AD,AE上,且AC=3,AB=2.5,EC=2,DB=3.5.求证:△ABC∽△AED.
14.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE?BF=EF?BC.
15.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
16.如图,在△ABC中,点D、E分别在AB、AC上,DE、BC的延长线相交于点F,且EF?DF=CF?BF.求证:△CAB∽△DAE.
17.如图,已知∠DAB=∠ECB,∠ABD=∠CBE.求证:△ABC∽△DBE.
18.如图,AC,BD相交于的点O,且∠ABO=∠C.
求证:△AOB∽△DOC.
19.如图,已知AD?AC=AB?AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
20.在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
参考答案
1.解:∵∠DAE=∠BAC,
∴当=时,△ADE∽△ACB,所以A选项符合题意,B选项不符合题意;
当∠AED=∠B,△ADE∽△ACB,所以C选项不符合题意;
当∠AED=∠C,△ADE∽△ABC,所以D选项不符合题意;
故选:A.
2.解:A、同旁内角互补,两直线平行,故原命题错误,是假命题,不符合题意;
B、对角线相等的平行四边形是矩形,故原命题错误,是假命题,不符合题意;
C、对角线互相垂直的平行四边形是菱形,故原命题错误,是假命题,不符合题意;
D、两角分别相等的两个三角形相似,正确,是真命题,符合题意,
故选:D.
3.解:A、只有一组角对应相等的两个三角形不一定相似;故A不符合题意;
B、两边对应成比例,但夹角不相等的两个三角形不一定相似,故B不符合题意;
C、两边对应成比例且夹角相等的两个三角形相似,故C符合题意;
故选:C.
4.解:①、当∠ACP=∠B,
∵∠A=∠A,
∴△APC∽△ACB,
∴①不符合题意;
②、当∠APC=∠ACB,
∵∠A=∠A,
∴△APC∽△ACB,
∴②不符合题意;
③、当AC2=AP?AB,
即AC:AB=AP:AC,
∵∠A=∠A
∴△APC∽△ACB,
∴③不符合题意;
④、∵当AB?CP=AP?CB,即PC:BC=AP:AB,
而∠PAC=∠CAB,
∴不能判断△APC和△ACB相似,
∴④符合题意;
故选:D.
5.解:A、∠C=∠E=98°,不是对应角相等,故不能判定△ABC∽△DEF;
B、两个三角形的三边不对应成比例,故不能判定△ABC∽△DEF;
C、两个直角三角形的两边不对应成比例,故不能判定△ABC∽△DEF;
D、如图,AG⊥BC,DH⊥EF,
∴∠AGB=∠DHE=90°,
∵∠B=∠E=35°,
∴△ABG∽△DEH,
∴,
∵BC=10,EF=5,
∴,
∴,
∴△ABC∽△DEF.
故选:D.
6.解:第一个三角形的三边的三边之比为:1:2:,
第二个三角形的三边的三边之比为:::,
第三个三角形的三边的三边之比为:1:2:,
第一个四角形的三边的三边之比为:1:1:,
只有第一和第三个三角形的三边成比例,
所以只有第一和第三个三角形相似,
故选:A.
7.解:因为△A1B1C1中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,
故选:B.
8.解:①阴影部分的三角形与原三角形有两个角相等,故两三角形相似;
②阴影部分的三角形与原三角形有两个角相等,故两三角形相似;
③两三角形的对应边不成比例,故两三角形不相似;
④两三角形对应边成比例且夹角相等,故两三角形相似.
故选:B.
9.解:∵等腰△ABC的底角为75°,
∴等腰△ABC的三角分别为30°,75°,75°,
∴一定与△ABC相似的是顶角为30°的等腰三角形,
故选:A.
10.解:∵BD⊥AC,AE⊥BC,
∴∠BDC=∠AEC=90°,
∴∠DBC+∠C=∠EAC+∠C=90°,
∴∠DBC=∠EAC,
∴△ACE∽△BCD,
又∵∠ADF=∠BDC=90°,
∴△AFD∽△BCD,
∵∠FBE=∠DBC,∠BEF=∠BDC=90°,
∴△BFE∽△BCD,
∴一定与△BCD相似的是△BFE,△AFD,△ACE,
故不一定与△BCD相似的是△BAE.
故选:D.
11.证明:∵PC=PD,
∴∠PCD=∠PDC,
∵∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,
又∵∠A=∠BPD,
∴∠B=∠APC,
∴△APC∽△PBD.
12.证明:∵四边形ABCD为矩形,
∴∠C=90°,AD∥BC,
∴∠ADF=∠DEC,
∵AF⊥DE,
∴∠AFD=∠C=90°,
∴△DEC∽△ADF.
13.证明:∵AC=3,AB=2.5,EC=2,DB=3.5.
∴AE=5,AD=6,
∴,,
∴,
∵∠A=∠A,
∴△ABC∽△AED.
14.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)如图,连接DE,
∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE?BF=EF?BC
15.解:∵∠BAC=∠BDC,∠AOB=∠DOC,
∴∠ABE=∠ACD
又∵∠BAC=∠DAE
∴∠BAC+∠EAC=∠DAE+∠EAC
∴∠DAC=∠EAB
∴△ABE∽△ACD.
16.证明:∵EF?DF=CF?BF.
∴,
∵∠EFC=∠BFD,
∴△EFC∽△BFD,
∴∠CEF=∠B,
∴∠B=∠AED,
∵∠CAB=∠DAE,
∴△CAB∽△DAE.
17.证明:∵∠DAB=∠ECB,∠ABD=∠CBE,
∴△ABD∽△CBE,
∴=,
即,
∵∠ABC=∠ABD+∠DBC,∠DBE=∠DBC+CBE,
∵,∠ABC=∠DBE,
∴△ABC∽△DBE.
18.证明:∵AC,BD相交于的点O,
∴∠AOB=∠DOC,
又∵∠ABO=∠C,
∴△AOB∽△DOC.
19.证明:∵AD?AC=AB?AE,
∴=,
∵∠DAE=∠BAC.
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC,
∴△DAB∽△EAC.
20.解(1),
∴=.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴=.
综合以上可得,DE=或.
同步能力提高训练(附答案)
一.选择题
1.如图,点D,E分别在△ABC的AB,AC边上,增加下列哪个条件不能使△ADE与△ABC相似?( )
A.=
B.=
C.∠AED=∠B
D.∠AED=∠C
2.下列命题是真命题的是( )
A.同旁内角相等,两直线平行
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.两角分别相等的两个三角形相似
3.下列可以判定△ABC∽△A'B'C'的条件是( )
A.∠A=∠B'=∠C'
B.=且∠A=∠C'
C.=且∠A=∠A'
D.以上条件都不对
4.如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP?AB;④AB?CP=AP?CB,不能判定△APC与△ACB相似的是( )
A.①
B.②
C.③
D.④
5.下列条件中,能使△ABC∽△DEF成立的是( )
A.∠C=98°,∠E=98°,
B.AB=1,AC=1.5,BC=2,EF=8,DE=10,FD=6
C.∠A=∠F=90°,AC=5,BC=13,DF=10,EF=26
D.∠B=35°,BC=10,BC上的高AG=7,∠E=35°,EF=5,EF上的高DH=3.5
6.如图所示的4个三角形中,相似三角形有( )
A.1对
B.2对
C.3对
D.4对
7.图形中,每个小网格均为正方形网格,带阴影部分的三角形中与如图△A1B1C1相似的是( )
A.
B.
C.
D.
8.如图,在三角形纸片中,∠A=80°,AB=6,AC=8.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形相似的有( )
A.①②③
B.①②④
C.①③④
D.①②③④
9.已知等腰△ABC的底角为75°,则下列三角形一定与△ABC相似的是( )
A.顶角为30°的等腰三角形
B.顶角为40°的等腰三角形
C.等边三角形
D.顶角为75°的等腰三角形
10.如图,在△ABC中,BD⊥AC于点D,AE⊥BC于点E,交BD于点F,下列三角形中不一定与△BCD相似的是( )
A.△BFE
B.△AFD
C.△ACE
D.△BAE
二.解答题
11.如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠A=∠BPD,求证:△APC∽△PBD.
12.如图,在矩形ABCD中,点E为BC上一点,连接DE,过点A作AF⊥DE于点F,求证:△DEC∽△ADF.
13.如图,点B,C分别在△ADE的边AD,AE上,且AC=3,AB=2.5,EC=2,DB=3.5.求证:△ABC∽△AED.
14.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE?BF=EF?BC.
15.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
16.如图,在△ABC中,点D、E分别在AB、AC上,DE、BC的延长线相交于点F,且EF?DF=CF?BF.求证:△CAB∽△DAE.
17.如图,已知∠DAB=∠ECB,∠ABD=∠CBE.求证:△ABC∽△DBE.
18.如图,AC,BD相交于的点O,且∠ABO=∠C.
求证:△AOB∽△DOC.
19.如图,已知AD?AC=AB?AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
20.在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
参考答案
1.解:∵∠DAE=∠BAC,
∴当=时,△ADE∽△ACB,所以A选项符合题意,B选项不符合题意;
当∠AED=∠B,△ADE∽△ACB,所以C选项不符合题意;
当∠AED=∠C,△ADE∽△ABC,所以D选项不符合题意;
故选:A.
2.解:A、同旁内角互补,两直线平行,故原命题错误,是假命题,不符合题意;
B、对角线相等的平行四边形是矩形,故原命题错误,是假命题,不符合题意;
C、对角线互相垂直的平行四边形是菱形,故原命题错误,是假命题,不符合题意;
D、两角分别相等的两个三角形相似,正确,是真命题,符合题意,
故选:D.
3.解:A、只有一组角对应相等的两个三角形不一定相似;故A不符合题意;
B、两边对应成比例,但夹角不相等的两个三角形不一定相似,故B不符合题意;
C、两边对应成比例且夹角相等的两个三角形相似,故C符合题意;
故选:C.
4.解:①、当∠ACP=∠B,
∵∠A=∠A,
∴△APC∽△ACB,
∴①不符合题意;
②、当∠APC=∠ACB,
∵∠A=∠A,
∴△APC∽△ACB,
∴②不符合题意;
③、当AC2=AP?AB,
即AC:AB=AP:AC,
∵∠A=∠A
∴△APC∽△ACB,
∴③不符合题意;
④、∵当AB?CP=AP?CB,即PC:BC=AP:AB,
而∠PAC=∠CAB,
∴不能判断△APC和△ACB相似,
∴④符合题意;
故选:D.
5.解:A、∠C=∠E=98°,不是对应角相等,故不能判定△ABC∽△DEF;
B、两个三角形的三边不对应成比例,故不能判定△ABC∽△DEF;
C、两个直角三角形的两边不对应成比例,故不能判定△ABC∽△DEF;
D、如图,AG⊥BC,DH⊥EF,
∴∠AGB=∠DHE=90°,
∵∠B=∠E=35°,
∴△ABG∽△DEH,
∴,
∵BC=10,EF=5,
∴,
∴,
∴△ABC∽△DEF.
故选:D.
6.解:第一个三角形的三边的三边之比为:1:2:,
第二个三角形的三边的三边之比为:::,
第三个三角形的三边的三边之比为:1:2:,
第一个四角形的三边的三边之比为:1:1:,
只有第一和第三个三角形的三边成比例,
所以只有第一和第三个三角形相似,
故选:A.
7.解:因为△A1B1C1中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,
故选:B.
8.解:①阴影部分的三角形与原三角形有两个角相等,故两三角形相似;
②阴影部分的三角形与原三角形有两个角相等,故两三角形相似;
③两三角形的对应边不成比例,故两三角形不相似;
④两三角形对应边成比例且夹角相等,故两三角形相似.
故选:B.
9.解:∵等腰△ABC的底角为75°,
∴等腰△ABC的三角分别为30°,75°,75°,
∴一定与△ABC相似的是顶角为30°的等腰三角形,
故选:A.
10.解:∵BD⊥AC,AE⊥BC,
∴∠BDC=∠AEC=90°,
∴∠DBC+∠C=∠EAC+∠C=90°,
∴∠DBC=∠EAC,
∴△ACE∽△BCD,
又∵∠ADF=∠BDC=90°,
∴△AFD∽△BCD,
∵∠FBE=∠DBC,∠BEF=∠BDC=90°,
∴△BFE∽△BCD,
∴一定与△BCD相似的是△BFE,△AFD,△ACE,
故不一定与△BCD相似的是△BAE.
故选:D.
11.证明:∵PC=PD,
∴∠PCD=∠PDC,
∵∠A+∠APC=∠PCD,∠B+∠BPD=∠PDC,
又∵∠A=∠BPD,
∴∠B=∠APC,
∴△APC∽△PBD.
12.证明:∵四边形ABCD为矩形,
∴∠C=90°,AD∥BC,
∴∠ADF=∠DEC,
∵AF⊥DE,
∴∠AFD=∠C=90°,
∴△DEC∽△ADF.
13.证明:∵AC=3,AB=2.5,EC=2,DB=3.5.
∴AE=5,AD=6,
∴,,
∴,
∵∠A=∠A,
∴△ABC∽△AED.
14.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)如图,连接DE,
∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE?BF=EF?BC
15.解:∵∠BAC=∠BDC,∠AOB=∠DOC,
∴∠ABE=∠ACD
又∵∠BAC=∠DAE
∴∠BAC+∠EAC=∠DAE+∠EAC
∴∠DAC=∠EAB
∴△ABE∽△ACD.
16.证明:∵EF?DF=CF?BF.
∴,
∵∠EFC=∠BFD,
∴△EFC∽△BFD,
∴∠CEF=∠B,
∴∠B=∠AED,
∵∠CAB=∠DAE,
∴△CAB∽△DAE.
17.证明:∵∠DAB=∠ECB,∠ABD=∠CBE,
∴△ABD∽△CBE,
∴=,
即,
∵∠ABC=∠ABD+∠DBC,∠DBE=∠DBC+CBE,
∵,∠ABC=∠DBE,
∴△ABC∽△DBE.
18.证明:∵AC,BD相交于的点O,
∴∠AOB=∠DOC,
又∵∠ABO=∠C,
∴△AOB∽△DOC.
19.证明:∵AD?AC=AB?AE,
∴=,
∵∠DAE=∠BAC.
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC,
∴△DAB∽△EAC.
20.解(1),
∴=.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴=.
综合以上可得,DE=或.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
