25.5相似三角形的性质 综合型解答题同步优生辅导训练(Word版 附答案)2021-2022学年冀教版九年级数学上册
文档属性
| 名称 | 25.5相似三角形的性质 综合型解答题同步优生辅导训练(Word版 附答案)2021-2022学年冀教版九年级数学上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 672.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 12:52:03 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《25.5相似三角形的性质》综合型解答题
同步优生辅导训练(附答案)
1.如图,O为线段MN的中点,MP与NQ交于点H,∠QOP=∠M=∠N=α,且OQ交MP于D,OP交NH于E.
(1)写出图中两对相似三角形;并证明其中一对.
(2)连接DE,如果α=45°,MN=6,MD=4,求DE的长.
2.如图,M为菱形ABCD边BC上一点,连接AM交BD于点G,∠ABM=2∠BAM.
(1)若AG=2,求GM?DG的值.
(2)延长AM,DC交于点P,若点M为BC的中点,S△MBG=,则△PDG的面积为
.
3.如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD于点O,过点D作DE∥AC交BC的延长线于点E,且BC=CE.
(1)求证:四边形ABCD是菱形;
(2)若OD=DE,OC=1,求菱形ABCD的周长.
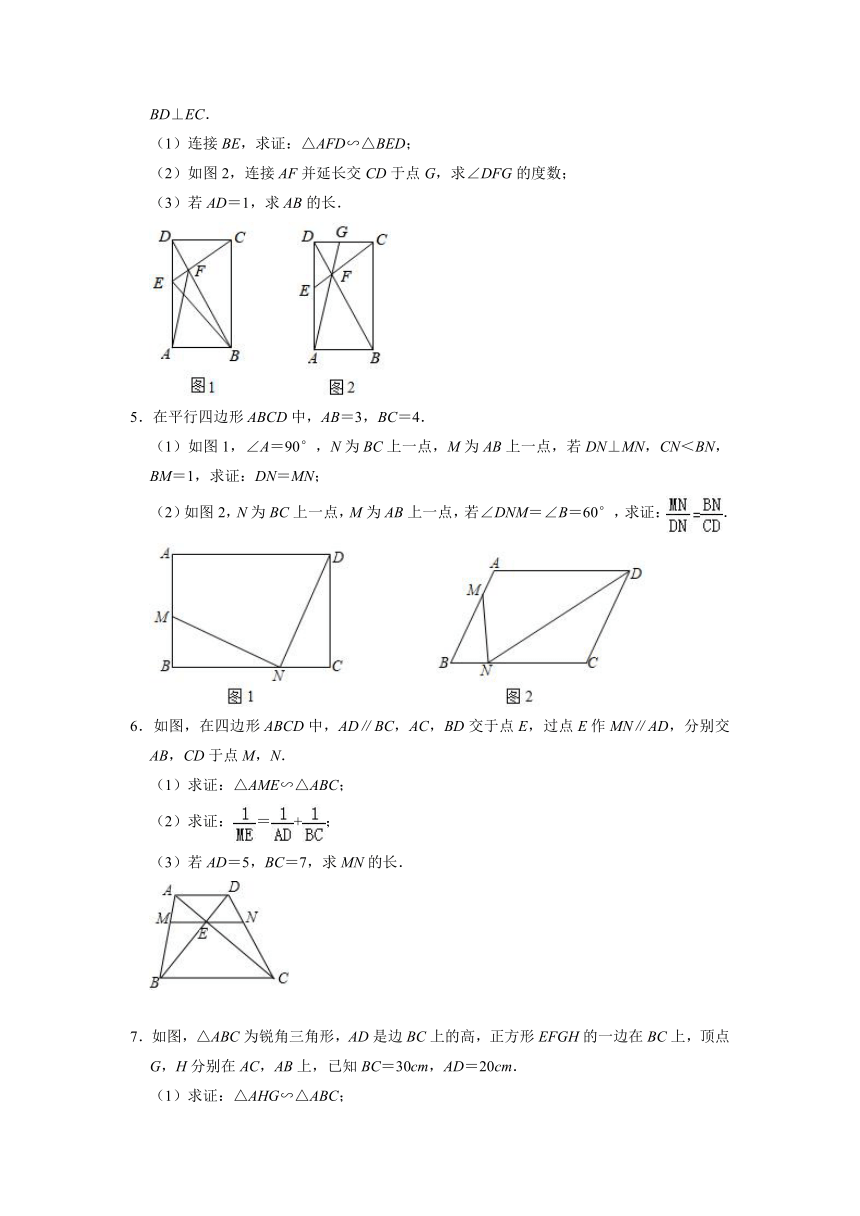
4.如图1,已知四边形ABCD是矩形,点E在AD上,AE=AB,EC与BD相交于点F,且BD⊥EC.
(1)连接BE,求证:△AFD∽△BED;
(2)如图2,连接AF并延长交CD于点G,求∠DFG的度数;
(3)若AD=1,求AB的长.
5.在平行四边形ABCD中,AB=3,BC=4.
(1)如图1,∠A=90°,N为BC上一点,M为AB上一点,若DN⊥MN,CN<BN,BM=1,求证:DN=MN;
(2)如图2,N为BC上一点,M为AB上一点,若∠DNM=∠B=60°,求证:.
6.如图,在四边形ABCD中,AD∥BC,AC,BD交于点E,过点E作MN∥AD,分别交AB,CD于点M,N.
(1)求证:△AME∽△ABC;
(2)求证:=+;
(3)若AD=5,BC=7,求MN的长.
7.如图,△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边在BC上,顶点G,H分别在AC,AB上,已知BC=30cm,AD=20cm.
(1)求证:△AHG∽△ABC;
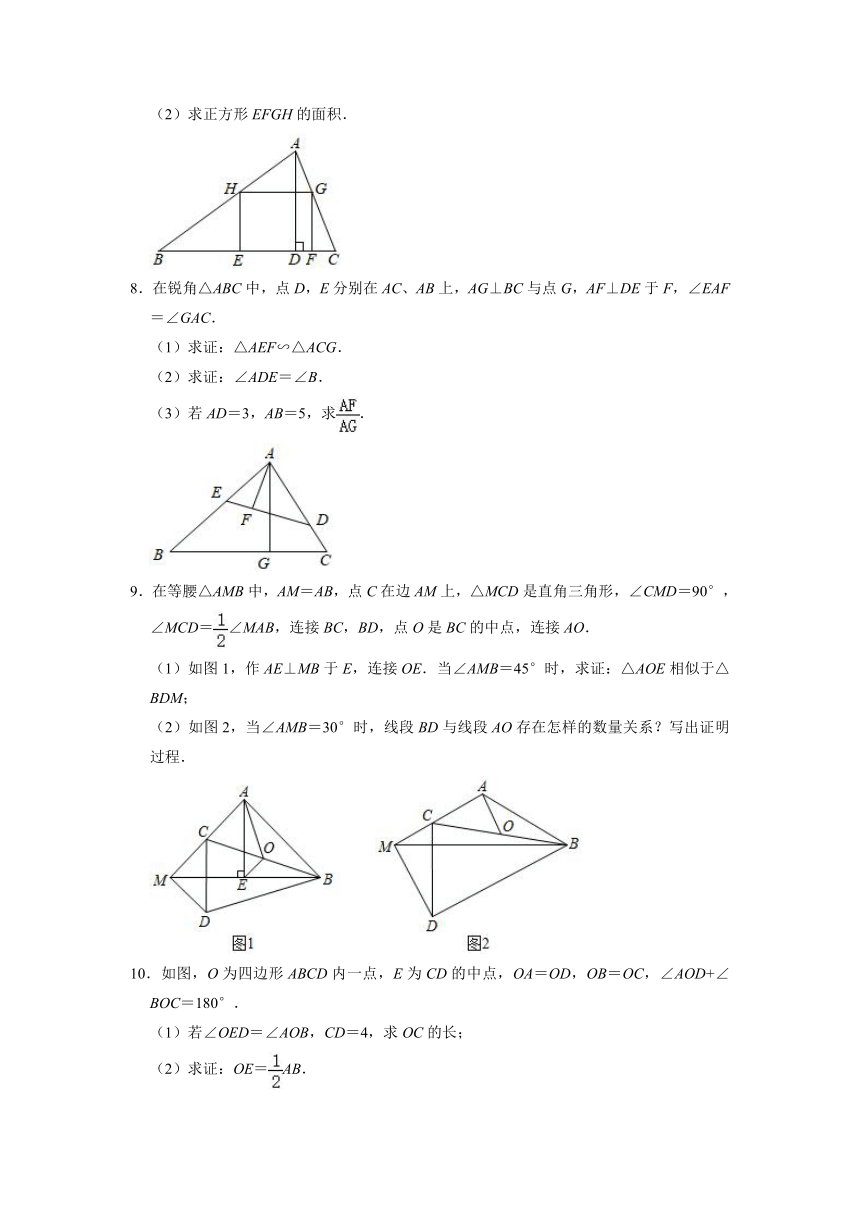
(2)求正方形EFGH的面积.
8.在锐角△ABC中,点D,E分别在AC、AB上,AG⊥BC与点G,AF⊥DE于F,∠EAF=∠GAC.
(1)求证:△AEF∽△ACG.
(2)求证:∠ADE=∠B.
(3)若AD=3,AB=5,求.
9.在等腰△AMB中,AM=AB,点C在边AM上,△MCD是直角三角形,∠CMD=90°,∠MCD=∠MAB,连接BC,BD,点O是BC的中点,连接AO.
(1)如图1,作AE⊥MB于E,连接OE.当∠AMB=45°时,求证:△AOE相似于△BDM;
(2)如图2,当∠AMB=30°时,线段BD与线段AO存在怎样的数量关系?写出证明过程.
10.如图,O为四边形ABCD内一点,E为CD的中点,OA=OD,OB=OC,∠AOD+∠BOC=180°.
(1)若∠OED=∠AOB,CD=4,求OC的长;
(2)求证:OE=AB.
11.如图,在Rt△ABC中,∠C=90°,点P是边AC上的一个动点,过点P作PQ∥AB交BC点Q,点D为线段PQ的中点,且AD平分∠BAC.
(1)求证:△ABC∽△PQC;
(2)若AB=13,BC=12,求AP的长.
12.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°.
(1)试说明:AC2=AB?AD;
(2)点E在边AB上,连接DE、CE,DE交AC于点F,若△AFD∽△CFE.试说明:点E为AB的中点.
13.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且∠ADE=∠B﹣∠A.
(1)求证:△CDE∽△ACB;
(2)若DA=,EA=1时,求CE的长.
14.如图,在四边形ABCD中,AB⊥AD,AB=2,BC=,CD=,DA=1.
(1)求证:∠BCD=45°;
(2)求AC的长.
15.如图,在△ABC中,AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连EF交AD于点G.
(1)求证:AD2=AB?AE;
(2)若AB=5,AE=4,求DG的值.
16.如图,已知BD是△ABC的角平分线,E是BD延长线上的一点,且AE=AB.
(1)求证:△ADE∽△CDB;
(2)若AB=6,BD=4,DE=5,求BC的长.
17.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥BC,EF∥AB.
(1)求证:△ADE∽△EFC.
(2)若=2,△EFC的面积是1,求△ADE的面积.
18.已知:如图,在△ABC中,AD⊥BC,垂足为点D,AD=BD,点E为边AD上一点,且DE=DC,联结BE并延长,交边AC于点F.
(1)求证:BF⊥AC;
(2)过点A作BC的平行线交BF的延长线于点G,联结CG.如果DE2=AE?AD,求证:四边形ADCG是矩形.
19.如图,在△ABC中,D,E分别是AB,AC上的点,△ADE∽△ACB.△ABC的角平分线AF交DE于点G,交BC于点F.
(1)求证:△ADG∽△ACF;
(2)若AE:AB=2:3,求的值.
20.如图,在?ABCD中,点G是边BC延长线上一点,联结AG分别交BD和CD于点E和F,联结DG.
(1)求证:AE2=EF?EG;
(2)如果∠ABD=∠AGD,求证:四边形ABGD是等腰梯形.
21.如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
(1)求证:AC2=CD?BC.
(2)过E做EG⊥AB,延长EG至点F,使FG=EG,若∠B=30°,求证:四边形AFEC是菱形.
22.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证△ADF∽△EAB;
(2)若AB=12,BC=10,求DF的长.
23.如图,△ABC中,∠ACB=90°,过点A作射线AP⊥AB,点D是线段AC上一动点(不与点A、C重合),连接BD,过点D作DE⊥BD,交射线AP于点E.
(1)如图①,当∠BAC=45°时,猜想线段AE与线段CD的数量关系,并说明理由;
(2)如图②,当∠BAC=30°时,猜想线段AE与线段CD的数量关系,并说明理由;
(3)当∠BAC=α时,直接写出线段AE与线段CD的数量关系.(用含α的式子表示)
24.如图,已知在△ABC中,BC>AB,BD平分∠ABC,交边AC于点D,E是BC边上一点,且BE=BA,过点A作AG∥DE,分别交BD、BC于点F、G,联结FE.
(1)求证:四边形AFED是菱形;
(2)求证:AB2=BG?BC;
(3)若AB=AC,BG=CE,联结AE,求的值.
25.已知:如图,在正方形ABCD中,联结BD,E是边AB上一点,BF⊥DE,垂足为点F,且EF?BD=BE?BF.
(1)求证:∠ADE=∠BDE;
(2)延长DF与CB的延长线交于点G,求证:BG=BC+AE.
26.如图,在?ABCD中,∠BAD的平分线交边BC于点E,交DC的延长线于点F,点G在AE上,联结GD,∠GDF=∠F.
(1)求证:AD2=DG?AF;
(2)联结BG,如果BG⊥AE,且AB=6,AD=9,求AF的长.
27.如图,在△ABC中,AD是角平分线,点E,点F分别在线段AB,AD上,且∠EFD=∠BDF.
(1)求证:△AFE∽△ADC.
(2)若=,=2,且∠AFE=∠C,探索BE和DF之间的数量关系.
28.如图,已知,在平行四边形ABCD中,E为射线CB上一点,联结DE交对角线AC于点F,∠ADE=∠BAC.
(1)求证:CF?CA=CB?CE;
(2)如果AC=DE,求证:四边形ABCD是菱形.
29.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且∠ADE=∠B﹣∠A.
(1)求证:△CDE∽△ABC;
(2)当DA:EA=:1时,求△CDE与△ABC的面积比.
30.已知正方形ABCD中,点E是边CD上的一点(点E不与C、D两点重合).
(1)如图1,AE平分∠CAD,将△ADE绕点A顺时针旋转90°得△ABF,连接EF,交AB于点G.求证△AFG∽△ACE;
(2)如图2,点E为CD的中点,将△ADE沿AE所在的直线折叠,使点D落在F处,若AB=4,求BF的长.
参考答案
1.解:(1)①△MOD∽△NEO,②△QOE∽△QNO,证明如下:
①∵∠QOP=∠M=∠N,
∴∠MOD+∠EON=180°﹣α,∠OEN+∠EON=180°﹣α,
∴∠MOD=∠OEN,
∵∠M=∠N,
∴△MOD∽△NEO;
②∵∠QEO是△OEN的外角,∠N=α,
∴∠QEO=∠N+∠EON=α+∠EON,
又∵∠QON=∠QOE+∠EON=α+∠EON,
∴∠QEO=∠QON,
∵∠QOE=∠N=α,
∴△QOE∽△QNO.
(2)∵∠M=∠N=α=45°,
∴∠MHN=90°,MH=NH,
∴△MHN是等腰直角三角形,
∵MN=6,点O是MN的中点,
∴MH=NH=6,MO=NO=3,
∵△MOD∽△NEO,
∴,
∴,
∴EN=,
∴DH=MH﹣MD=6﹣4=2,EH=NH﹣EN=6﹣=,
∴DE==.
2.解:(1)∵四边形ABCD是菱形,
∴AD∥BC,∠ABM=2∠ABD,
∵∠ABM=2∠BAM,
∴∠ABD=∠BAM,
∴AG=BG=2,
∵AD∥BC,
∴∠DAG=∠BMG,∠ADG=MBG,
∴△ADG∽△MBG,
∴,
∴GM?DG=AG?BG=4;
(2)如图,连接CG,
∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,
∴∠BAM=∠CPM,∠ABM=∠PCM,
∴△ABM∽△PCM,
同理,△ABG∽△PDG,
∵M为BC的中点,
∴BM=CM,S△BGM=S△CGM=,
∵△ABM∽△PCM,
∴=1,
∴AB=PC=CD,
∵△ABG∽△PDG,
∴=,
∴==2,
∴S△DGC=2S△BGC=3,
∵PC=DC,
∴S△DGC=S△PCG=3,
∴S△PDG=S△DGC+S△PCG=6,
故答案为:6.
3.解:(1)∵AD∥BC,DE∥AC,
∴四边形ACED是平行四边形,
∴AD=CE,
∵BC=CE,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴?ABCD是菱形;
(2)由(1)知,四边形ACED是平行四边形,
∴AC=DE,
∵OD=DE,
∴OD=AC,
∵四边形ABCD是菱形,
∴OA=OC=1,
∴OD=AC=2,
∵∠COD=90°,
∴CD===,
∴菱形ABCD的周长=4CD=4.
4.(1)证明:∵四边形ABCD是矩形,BD⊥EC,
∴∠DFE=∠DAB=90°,
∵∠FDE=∠ADB,
∴△FDE∽△ADB,
∴=,
∵∠EDB=∠FDA,
∴△AFD∽△BED;
(2)解:连接BE,
∵△AFD∽△BED,
∴∠DFA=∠DEB,
∴∠BEA=∠BFA,
∵AE=AB,∠DAB=90°,
∴∠BEA=45°,
∴∠BFA=45°,
∴∠DFG=∠BFA=45°;
(3)解:∵四边形ABCD是矩形,
∴AB=CD,∠CDE=∠DAB=90°,
∵BD⊥EC,
∴∠ADB=∠DCE,
∴△CDE∽△DAB,
∴=,
设AB的长为x,则DE=1﹣x,
∴=,
解得x1=,x2=(舍去),
∴AB的长为.
5.证明:(1)根据题意可知AB=CD=3,BC=AD=4,∠B=∠C=∠A=90°,
不妨设CN=x,则BN=4﹣x,
∵DN⊥MN,
∴∠MNB+∠DNC=90°,
又∠DNC+∠NDC=90°,
∴∠MNB=∠NDC,
∴△BMN∽△CND,
∴,即,
解得x=1或x=3,
∵CN<BN,
∴x=1,
∴CN=BM=1,BN=DC=3,DN==,MN==,
∴DN=MN;
(2)如下图,
过点D作DE=DN,并与BC的延长线交于点E,
则∠E=∠DNE,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC=60°,
∵AD∥BC,
∴∠ADC=∠DCE=60°,∠ADN=∠DNE,
∴∠B=DCE=∠DNM=60°,
∵∠BMN+∠MNB=120°,∠MNB+∠DNE=120°,
∴∠BMN=∠DNE,
∴∠BMN=∠E,
∴△BMN∽△CED,
∴
∴.
6.(1)证明:∵AD∥BC,MN∥AD,
∴MN∥BC,
∴△AME∽△ABC;
(2)证明:∵MN∥AD,AD∥BC,
∴=,
∵MN∥BC,
∴△AME∽△ABC,△DEN∽△DBC,
∴=,=,∴=,
∴ME=NE,
∴点E是MN的中点,ME=NE=MN,
∵AD∥BC∥MN,
∴△CEN∽△CAD,△AME∽△ABC,
∴=,=,
∴+=+==1,
∴+=1,
∴=+.
(3)结合(2)的结论,
∵AD=5,BC=7,
∴=,
∴ME=,
∵ME=NE,
∴MN=ME+NE=+=.
7.(1)证明:∵四边形EFGH为正方形,
∴GH∥EF.
∴GH∥BC,
∴△AHG∽△ABC.
解:(2)设AD与HG的交点为M,如图,
则AM是△AHG的高.
由(1)知:△AHG∽△ABC.
∴.
∵四边形EFGH为正方形,
∴HG=HE=FG,HG∥BC.
∵AD⊥BC,
∴MD=FG.
∴HG=MD.
设HG=MD=xcm,则AM=AD﹣MD=(20﹣x)cm,
∴.
解得:x=12,
∴正方形EFGH的边长为12cm.
∴正方形EFGH的面积为:12×12=144cm2
8.证明:(1)∵AG⊥BC,AF⊥DE于,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC
∴△AEF∽△ACG.
(2)由(1)知△AEF∽△ACG,
∴∠AEF=∠C
∵∠DAE=∠BAC(公共角),
∴△EAD∽△CAB.
∴∠ADE=∠B.
解:(3)由(2)知:△ADE∽△ABC,
∴.
由(1)知△AEF∽△ACG,
∴.
∴.
∵AD=3,AB=5,
∴.
9.解:(1)证明:∵AM=AB,AE⊥MB,
∴E为MB的中点,
∵∠AMB=45°,
∴∠MAB=180°﹣2×45°=90°,
∴AE=MB,
∵点O是BC的中点,
∴OE∥MC且OE=MC,
∴∠OEB=∠CMB=45°,
∴∠AEO=45°,
∵∠CMD=90°,
∴∠BMD=45°,
∴∠BMD=∠AEO,
∴△BMD∽△AEO;
(2)BD=AO;
证明:如图,作AF⊥MB于F,连接OF,
∵AM=AB,AF⊥MB,
∴F为MB的中点,
∵∠AMB=30°,
∴∠MAB=180°﹣2×30°=120°,
∴∠MCD=∠MAB=60°,
∵∠CMD=90°,
∴∠CDM=30°,
∴tanAMB=tan∠CDM=tan30°==,
∴MB=2AF,
∵点O是BC的中点,
∴OF∥MC且OF=MC,
∴∠OFB=∠CMB=30°,MD=2OF,
∴∠AFO=60°,
∴∠BMD=∠AFO,
∴△BMD∽△AFO,
∴BD=AO.
10.解:(1)∵∠AOD+∠BOC=180°,
∴∠AOB+∠DOC=180°;
∵∠OED=∠AOB,
∴∠OED+∠DOC=180°;
∵∠OED+∠EDO+∠DOE=180°,
∴∠CDO=∠COE,
又∵∠DCO=∠OCE,
∴△DCO∽△OCE(AAA),
∴,即OC2=DC?CE;
∵E为CD的中点,CD=4,
∴CE=2,则OC===.
(2)
将△AOB绕点O逆时针方向旋转,使得OB与OC重合,得ΔA'OC,
∴∠AOB=∠A'OC,OA'=OA,AB=A'C;
∵由(1)得∠AOB+∠DOC=180°,
∴∠A'OC+∠DOC=180°,
∴点D,O,A'在同一直线上;
∵OA=OD,
∴OD=OA',即点O是线段DA'的中点,
又∵E为CD的中点,
∴EO是△DA'C的中位线,
∴OE=CA'=AB.
11.解:(1)∵PQ∥AB,
∴∠B=∠CQP,∠C=∠C=90°,
∴△ABC∽△PQC;
(2)过D作DE⊥AC交AC于点E,DF⊥AB交AB于点F,作CG⊥AB交AB于点G、PQ于点H,
∵AB=13,BC=12,
∴AC=5,
由Rt△ABC面积=×BC×AC=×AB×CG,
∴CG=,
∵PQ∥AB,
∴DF=HG,
∴CH=﹣DF,
在Rt△CHP中,sin∠CPH=sin∠BAC,
∴=,
∴CP=5﹣DF,
∵AD平分∠BAC,
∴DF=DE,
在Rt△DEP中,tan∠DPE==,
∴EP=DF,
∵D是PQ的中点,DE∥BC,
∴CP=2EP=DF,
∴5﹣DF=DF,
∴DF=,
∴CP=,
∴AP=5﹣=.
12.解:(1)∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠CB=90°.
∴△ADC∽△ACB,
∴=,
∴AC2=AB?AD;
(2)∵△AFD∽△CFE.
∴,
∴AD∥CE,
∴∠DAC=∠ACE,
∵∠DAC=∠CAB,
∴∠CAB=∠ACE,
∴AE=CE,
∵∠CAB+∠B=∠ACE+∠BCE=90°,
∴∠BCE=∠B,
∴BE=CE,
∴AE=BE,
∴点E为AB的中点.
13.(1)证明:∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A,
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B﹣∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B,
∴△CDE∽△ACB;
(2)解:∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB=,
∴AB=2,
∵△CDE∽△ACB,
∴,
即,
解得CE=3,CE=﹣4(舍),
∴CE=3.
14.(1)证明:连接BD,
在△BAD中,AB⊥AD,AB=2,DA=1,
则BD==,
在△CBD中,BC2+BD2=()2+()2=10=()2=CD2,
∴∠CBD=90°,
∵BD=BC=,
∴△CBD是等腰直角三角形,
∴∠BCD=45°;
(2)解:作CM⊥AB,交AB的延长线于M,
∵∠ABD+∠ADB=90°,∠ABD+∠CBM=90°,
∴∠ADB=∠CBM,
∵∠DAB=∠BMC=90°,
∴△ABD∽△MCB(AA),
∴=,即=,
解得BM=1,
在△CMB中,CM==2,
∴AM=2+1=3,
在△CMA中,AC===.
15.(1)证明:∵AD⊥BC,DE⊥AC,
∴∠ADC=∠AED=90°,
∵∠DAE=∠CAD,
∴△ADE∽△ACD,
∴AD:AC=AE:AD,
∴AD2=AC?AE,
又∵AB=AC,
∴AD2=AB?AE;
(2)解:连接DF,如图所示:
由(1)得:AD2=AB?AE,
∴AD2=AB?AE=5×4=20,
∴AD=2,
∵AB=AC,AD⊥BC,
∴BD=CD,
∵F是AB的中点,
∴DF是△ABC的中位线,
∴DF=AC=,DF∥AC,
∴△DFG∽△AEG,
∴===,
∴=,
∴DG=AD=×2=.
16.解:(1)∵BD是△ABC的角平分线,
∴∠ABD=∠CBD.
∵AB=AE,
∴∠ABD=∠E.
∴∠E=∠CBD.
∵∠EDA=∠BDC,
∴△ADE∽△CDB.
(2)∵AE=AB,AB=6,
∴AE=6.
∵△ADE∽△CDB,
∴.
∵BD=4,DE=5,
∴.
∴BC=.
17.解:(1)∵DE∥BC,
∴∠AED=∠ECF,∠ADE=∠ABC,
又∵EF∥AB,
∴∠EFC=∠ABC(两直线平行,同位角也相等),
∴∠ADE=∠EFC,
∴△ADE∽△EFC(两角对应相等的两三角形相似);
(2)∵AB∥EF,DE∥BC,
∴四边形BDEF是平行四边形,
∴EF=BD,
∵=2,
∴=2,
又∵△ADE∽△EFC,
∴=()2=22=4(相似△的面积比等于相似比的平方),
∵△EFC的面积为1,
∴S△ADE=4.
18.(1)证明:∵AD⊥BC,
∠ADC=∠BDE=90°,
在△ACD和△BED中,
,
∴△ACD≌△BED(SAS),
∴∠EBD=∠CAD,
又∵∠BED=∠AEF,
∴△BED∽△AEF,
∴∠AFE=∠EDB=90°,
即BF⊥AC;
(2)证明:∵AG∥BC,
∴∠AGE=∠EDB,
由(1)知∠EBD=∠CAD,
∴∠AGE=∠CAD,
又∵∠AEG=∠BED=∠ACD,
∴△AEG∽△DCA,
∴=,
∴AE?AD=DC?AG,
∵DE2=AE?AD,DE=DC,
∴DC?AG=DE2=DC2,
∴DC=AG,
又∵AG∥DC,
∴四边形ADCG是平行四边形,
∵AD⊥BC,
∴四边形ADCG是矩形(有一个角是直角的平行四边形是矩形).
19.解:(1)∵△ADE∽△ACB,
∴∠ADE=∠ACB,
又∵AF为∠BAC的角平分线,
∴∠DAG=∠FAC,
∴在△ADG与△ACF中,
∴△ADG∽△ACF;
(2)∵ADE∽△ACB,
∴==,
在△ADG∽△ACF时,
AG:AF=AD:AC=2:3,
设AG为2x,则AF=3x,
即GF=x,
∴=.
20.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴△ABE∽△FDE.
∴.
∴ADE∽△GBE.
∴.
∴.
∴AE2=EF?EG.
(2)∵AB∥CD,
∴∠ABD=∠CDB.
∵∠ABD=∠AGD,
∴∠CDB=∠AGD.
∵∠DEF=∠GED,
∴△DEF∽GED.
∴.
∴DE2=EF?EG.
由(1)知:AE2=EF?EG.
∴DE=AE.
在△ABE和△DEG中,
.
∴△ABE≌△DEG(AAS).
∴AB=DG.
∵AD∥BG,
∴四边形ABGD是等腰梯形.
21.证明:(1)∵AC平分∠BCD,
∴∠DCA=∠ACB.
又∵AC⊥AB,AD⊥AE,
∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.
又∵E是BC的中点,
∴AE=BE,
∴∠EAB=∠ABC,
∴∠DAC=∠ABC,
∴△ACD∽△BCA,
∴=,
∴AC2=CD?BC;
(2)∵AC⊥AB,∠B=30°,E是BC的中点,
∴AC=BC=EB=EC,
∵EG⊥AB,∠B=30°,
∴EG=EB,
又∵EG=FG,
∴2EG=FE=EB,
∴EF=AC,
∵EG⊥AB,FG=EG,
∴AF=AE=EB,
∴AF=FE=EC=CA,
∴四边形AFEC是菱形.
22.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ADF∽△EAB;
(2)解:∵BC=AD=10,E是BC边的中点,
∴BE=5,
∴AE===13,
由(1)得:△ADF∽△EAB,
∴=,
即=,
解得:DF=.
23.解:(1)AE=CD,
如图1,在BC上取一点G,使AD=BG,连接DG,
∵∠BAC=45°,∠ACB=90°,
∴△ACB是等腰直角三角形,
∴AC=BC,
∴AC﹣CD=BC﹣BG,
即CD=CG,
∴△CDG是等腰直角三角形,
∴DG=CD,∠DGC=45°,
∴∠DGB=135°,
∵AP⊥AB,
∴∠BAP=90°,
∵∠DAE=90°+45°=135°,
∴∠DAE=∠DGB,
∵DE⊥DB,
∴∠EDB=90°,
∴∠EDA+∠BDC=90°,
∵∠BDC+∠DBC=90°,
∴∠EDA=∠DBC,
∴△EAD≌△DGB(ASA),
∴AE=DG,
∴AE=CD;
(2)AE=2CD,理由是
如图2,
过D作DF∥AB,交BC于F,
则∠FDC=∠BAC=30°,,
∴,
∵AP⊥AB,DE⊥BD,
∴∠BAP=∠BDE=90°,
∵∠ADE+∠BDE+∠BDC=180°,
∴∠ADE+∠BDC=90°,
∵∠ACB=90°,∠FDC=30°
∴∠DBC+∠BDC=90°,CF=DF,
∴∠ADE=∠DBC,
∵∠DAE=∠BAC+∠BAP,∠BFD=∠FDC+∠ACB,
∴∠DAE=∠DBC,
∴△DAE∽△BFD,
∴,
∴,
∴,
∴=2,即AE=2CD;
(3)CD=AE?sinα,理由是
如图3,
过D作DF∥AB,交BC于F,
则∠FDC=∠BAC=α,,
∴,
∵AP⊥AB,DE⊥BD,
∴∠BAP=∠BDE=90°,
∵∠ADE+∠BDE+∠BDC=180°,
∴∠ADE+∠BDC=90°,
∵∠ACB=90°,∠FDC=α
∴∠DBC+∠BDC=90°,sin∠FDC=sinα=,
∴∠ADE=∠DBC,
∵∠DAE=∠BAC+∠BAP,∠BFD=∠FDC+∠ACB,
∴∠DAE=∠BFD,
∴△DAE∽△BFD,
∴,
∴,
∴=sinα,
∴CD=AE?sinα.
24.解:(1)证明:如图,
∵BD平分∠ABC,
∴∠ABF=∠EBF,
∵BA=BE,BF=BF,
∴△ABF≌△EBF(SAS),
∴AF=EF,
同理可得△ABD≌△EBD(SAS),
∴AD=ED,∠ADB=∠EDB,
∵AG∥DE,
∴∠AFD=∠EDF,
∴∠AFD=∠ADF,
∴AF=AD,
∴AF=FE=ED=DA,
∴四边形AFED是菱形.
(2)证明:由(1)得△ABF≌△EBF,
∴∠BAG=∠BEF,
∵四边形AFED是菱形,
∴AD∥FE,
∴∠BEF=∠C,
∴∠BAG=∠C,
∵∠ABG=∠CBA,
∴△ABG∽△CBA,
∴,即AB2=BG?BC.
(3)由(2)得,△ABG∽△CBA,AB=AC,
∴AG=BG,
∴∠GAB=∠GBA,
∴∠AGC=2∠GAB,
∵BG=CE,
∴BE=CG,
∴CG=CA,
∴∠CAG=∠CGA,
∵∠CAG=2∠DAE,
∴∠DAE=∠ABC,
∴∠DEA=∠ACB,
∴△DAE∽△ABC,
∴=()2,
∵AB2=BG?BC,AB=BE,BG=EC,
∴BE2=EC?BC,
∴点E是BC的黄金分割点,
∴=,
∴=,
∵∠EAC=∠C,
∴CE=AE,
∴=,
∴=.
25.解:(1)证明:∵BF⊥DE,
∴∠BFD=90°,
在Rt△BEF中,sin∠EBF=,
在Rt△DBF中,sin∠BDE=,
∵EF?BD=BE?BF,
∴=,
∴sin∠EBF=sin∠BDE,
∴∠EBF=∠BDE,
∵正方形ABCD,
∴∠DAE=90°=∠BFD,
∴∠EBF+∠BEF=∠ADE+∠AED=90°,
∵∠BEF=∠AED,
∴∠EBF=∠ADE,
∴∠ADE=∠BDE;
(2)证明:如图,延长BF交DA的延长线于H,
∵∠ADE=∠BDE,∠DFH=∠DFB=90°,DF=DF,
∴△DFH≌△DFB(ASA),
∴HF=BF,
∵正方形ABCD,
∴AD∥BC,AD=AB=BC,
∴∠G=∠ADE,∠GBF=∠H,
在△GBF和△DHF中,
,
∴△GBF≌△DHF(AAS),
∴BG=DH=AD+AH=BC+AH,
在△DAE和△BAH中,
,
∴△DAE≌△BAH(ASA),
∴AH=AE,
∴BG=BC+AE.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,AD∥BC,
∵AE平分∠BAD,
∴∠BAF=∠DAF=∠F,
∴AD=DF,
∵∠GDF=∠F,
∴△GDF∽△DAF,
∴=,
∴AD2=DG?AF;
(2)解:∵AF平分∠BAD,
∴∠BAE=∠DAF,
∵AD∥BC,
∴∠BEA=∠DAF,
∴∠BEA=∠BAE,
∵BG⊥AE,AB=6,AD=9,
∴BA=BE=6,
∵∠BEA=∠CEF,
∴∠CEF=∠F,
∴EC=CF=3,DF=AD=9,
∴==,
即AG=GE=EF,
∵AD2=DG?AF,
∴AF2=81,
∴AF=.
27.解:(1)∵AD为∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠EFD=∠BDF,
∴180°﹣∠EFD=180°﹣∠BDF,
∴∠AFE=∠ADC,
∴△AFE∽△ADC;
(2)由(1)得,△AFE∽△ADC,
∴∠AEF=∠C,
∵∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∵=,△AFE∽△ADC,
∴,
∴,
∵=2,AE=AF,
∴,
∴EB=2FD.
28.证明:(1)∵四边形ABCD是平行四边形.
∴AD∥BC.
∴∠ADE=∠E.
∵∠ADE=∠BAC.
∴∠BAC=∠E.
∵∠ACB=∠ECF.
∴△ACB∽△ECF.
∴.
∴CF?CA=CB?CE
(2)由(1)知∠ADE=∠E.
∵∠ADF=∠CFE.
∴△ADF∽△CEF.
∴.
∴.
∵AC=DE.
∴EF=CF.
∵△ACB∽△ECF.
∴AB=BC
∵四边形ABCD是平行四边形.
∴四边形ABCD是菱形.
29.(1)证明:∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A,
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B﹣∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B,
∴△CDE∽△ABC,
(2)解:令EA=k,DA=,CE=x,
∵△CDE∽△ABC,
∴,
即,
解得x=3k,x=﹣4k(舍),
所以.
30.解:(1)∵将△ADE绕点A顺时针旋转90°得△ABF,
∴∠DAE=∠BAF,AE=AF,
∴△AEF是等腰直角三角形,
∴∠AFE=45°,
∵AE平分∠DAC,
∴∠DAE=∠EAC,
∴∠FAB=∠CAE,
在正方形ABCD中,∠ACD=45°,
∴∠ACD=∠AFE,
∴△AFG∽△ACE,
(2)过F作BC平行线交AB,CD于G,H,
∴△AGF∽△FHE,
∵,
设FH=x,
则AG=2x,GF=4﹣x,EH=,
∵AG=DH,
∴2x=2+,
解得x=,
∴AG=,GF=4﹣=,
∴BG=4﹣=,
在Rt△BGF中,BF=.
同步优生辅导训练(附答案)
1.如图,O为线段MN的中点,MP与NQ交于点H,∠QOP=∠M=∠N=α,且OQ交MP于D,OP交NH于E.
(1)写出图中两对相似三角形;并证明其中一对.
(2)连接DE,如果α=45°,MN=6,MD=4,求DE的长.
2.如图,M为菱形ABCD边BC上一点,连接AM交BD于点G,∠ABM=2∠BAM.
(1)若AG=2,求GM?DG的值.
(2)延长AM,DC交于点P,若点M为BC的中点,S△MBG=,则△PDG的面积为
.
3.如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD于点O,过点D作DE∥AC交BC的延长线于点E,且BC=CE.
(1)求证:四边形ABCD是菱形;
(2)若OD=DE,OC=1,求菱形ABCD的周长.
4.如图1,已知四边形ABCD是矩形,点E在AD上,AE=AB,EC与BD相交于点F,且BD⊥EC.
(1)连接BE,求证:△AFD∽△BED;
(2)如图2,连接AF并延长交CD于点G,求∠DFG的度数;
(3)若AD=1,求AB的长.
5.在平行四边形ABCD中,AB=3,BC=4.
(1)如图1,∠A=90°,N为BC上一点,M为AB上一点,若DN⊥MN,CN<BN,BM=1,求证:DN=MN;
(2)如图2,N为BC上一点,M为AB上一点,若∠DNM=∠B=60°,求证:.
6.如图,在四边形ABCD中,AD∥BC,AC,BD交于点E,过点E作MN∥AD,分别交AB,CD于点M,N.
(1)求证:△AME∽△ABC;
(2)求证:=+;
(3)若AD=5,BC=7,求MN的长.
7.如图,△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边在BC上,顶点G,H分别在AC,AB上,已知BC=30cm,AD=20cm.
(1)求证:△AHG∽△ABC;
(2)求正方形EFGH的面积.
8.在锐角△ABC中,点D,E分别在AC、AB上,AG⊥BC与点G,AF⊥DE于F,∠EAF=∠GAC.
(1)求证:△AEF∽△ACG.
(2)求证:∠ADE=∠B.
(3)若AD=3,AB=5,求.
9.在等腰△AMB中,AM=AB,点C在边AM上,△MCD是直角三角形,∠CMD=90°,∠MCD=∠MAB,连接BC,BD,点O是BC的中点,连接AO.
(1)如图1,作AE⊥MB于E,连接OE.当∠AMB=45°时,求证:△AOE相似于△BDM;
(2)如图2,当∠AMB=30°时,线段BD与线段AO存在怎样的数量关系?写出证明过程.
10.如图,O为四边形ABCD内一点,E为CD的中点,OA=OD,OB=OC,∠AOD+∠BOC=180°.
(1)若∠OED=∠AOB,CD=4,求OC的长;
(2)求证:OE=AB.
11.如图,在Rt△ABC中,∠C=90°,点P是边AC上的一个动点,过点P作PQ∥AB交BC点Q,点D为线段PQ的中点,且AD平分∠BAC.
(1)求证:△ABC∽△PQC;
(2)若AB=13,BC=12,求AP的长.
12.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°.
(1)试说明:AC2=AB?AD;
(2)点E在边AB上,连接DE、CE,DE交AC于点F,若△AFD∽△CFE.试说明:点E为AB的中点.
13.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且∠ADE=∠B﹣∠A.
(1)求证:△CDE∽△ACB;
(2)若DA=,EA=1时,求CE的长.
14.如图,在四边形ABCD中,AB⊥AD,AB=2,BC=,CD=,DA=1.
(1)求证:∠BCD=45°;
(2)求AC的长.
15.如图,在△ABC中,AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连EF交AD于点G.
(1)求证:AD2=AB?AE;
(2)若AB=5,AE=4,求DG的值.
16.如图,已知BD是△ABC的角平分线,E是BD延长线上的一点,且AE=AB.
(1)求证:△ADE∽△CDB;
(2)若AB=6,BD=4,DE=5,求BC的长.
17.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥BC,EF∥AB.
(1)求证:△ADE∽△EFC.
(2)若=2,△EFC的面积是1,求△ADE的面积.
18.已知:如图,在△ABC中,AD⊥BC,垂足为点D,AD=BD,点E为边AD上一点,且DE=DC,联结BE并延长,交边AC于点F.
(1)求证:BF⊥AC;
(2)过点A作BC的平行线交BF的延长线于点G,联结CG.如果DE2=AE?AD,求证:四边形ADCG是矩形.
19.如图,在△ABC中,D,E分别是AB,AC上的点,△ADE∽△ACB.△ABC的角平分线AF交DE于点G,交BC于点F.
(1)求证:△ADG∽△ACF;
(2)若AE:AB=2:3,求的值.
20.如图,在?ABCD中,点G是边BC延长线上一点,联结AG分别交BD和CD于点E和F,联结DG.
(1)求证:AE2=EF?EG;
(2)如果∠ABD=∠AGD,求证:四边形ABGD是等腰梯形.
21.如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
(1)求证:AC2=CD?BC.
(2)过E做EG⊥AB,延长EG至点F,使FG=EG,若∠B=30°,求证:四边形AFEC是菱形.
22.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证△ADF∽△EAB;
(2)若AB=12,BC=10,求DF的长.
23.如图,△ABC中,∠ACB=90°,过点A作射线AP⊥AB,点D是线段AC上一动点(不与点A、C重合),连接BD,过点D作DE⊥BD,交射线AP于点E.
(1)如图①,当∠BAC=45°时,猜想线段AE与线段CD的数量关系,并说明理由;
(2)如图②,当∠BAC=30°时,猜想线段AE与线段CD的数量关系,并说明理由;
(3)当∠BAC=α时,直接写出线段AE与线段CD的数量关系.(用含α的式子表示)
24.如图,已知在△ABC中,BC>AB,BD平分∠ABC,交边AC于点D,E是BC边上一点,且BE=BA,过点A作AG∥DE,分别交BD、BC于点F、G,联结FE.
(1)求证:四边形AFED是菱形;
(2)求证:AB2=BG?BC;
(3)若AB=AC,BG=CE,联结AE,求的值.
25.已知:如图,在正方形ABCD中,联结BD,E是边AB上一点,BF⊥DE,垂足为点F,且EF?BD=BE?BF.
(1)求证:∠ADE=∠BDE;
(2)延长DF与CB的延长线交于点G,求证:BG=BC+AE.
26.如图,在?ABCD中,∠BAD的平分线交边BC于点E,交DC的延长线于点F,点G在AE上,联结GD,∠GDF=∠F.
(1)求证:AD2=DG?AF;
(2)联结BG,如果BG⊥AE,且AB=6,AD=9,求AF的长.
27.如图,在△ABC中,AD是角平分线,点E,点F分别在线段AB,AD上,且∠EFD=∠BDF.
(1)求证:△AFE∽△ADC.
(2)若=,=2,且∠AFE=∠C,探索BE和DF之间的数量关系.
28.如图,已知,在平行四边形ABCD中,E为射线CB上一点,联结DE交对角线AC于点F,∠ADE=∠BAC.
(1)求证:CF?CA=CB?CE;
(2)如果AC=DE,求证:四边形ABCD是菱形.
29.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且∠ADE=∠B﹣∠A.
(1)求证:△CDE∽△ABC;
(2)当DA:EA=:1时,求△CDE与△ABC的面积比.
30.已知正方形ABCD中,点E是边CD上的一点(点E不与C、D两点重合).
(1)如图1,AE平分∠CAD,将△ADE绕点A顺时针旋转90°得△ABF,连接EF,交AB于点G.求证△AFG∽△ACE;
(2)如图2,点E为CD的中点,将△ADE沿AE所在的直线折叠,使点D落在F处,若AB=4,求BF的长.
参考答案
1.解:(1)①△MOD∽△NEO,②△QOE∽△QNO,证明如下:
①∵∠QOP=∠M=∠N,
∴∠MOD+∠EON=180°﹣α,∠OEN+∠EON=180°﹣α,
∴∠MOD=∠OEN,
∵∠M=∠N,
∴△MOD∽△NEO;
②∵∠QEO是△OEN的外角,∠N=α,
∴∠QEO=∠N+∠EON=α+∠EON,
又∵∠QON=∠QOE+∠EON=α+∠EON,
∴∠QEO=∠QON,
∵∠QOE=∠N=α,
∴△QOE∽△QNO.
(2)∵∠M=∠N=α=45°,
∴∠MHN=90°,MH=NH,
∴△MHN是等腰直角三角形,
∵MN=6,点O是MN的中点,
∴MH=NH=6,MO=NO=3,
∵△MOD∽△NEO,
∴,
∴,
∴EN=,
∴DH=MH﹣MD=6﹣4=2,EH=NH﹣EN=6﹣=,
∴DE==.
2.解:(1)∵四边形ABCD是菱形,
∴AD∥BC,∠ABM=2∠ABD,
∵∠ABM=2∠BAM,
∴∠ABD=∠BAM,
∴AG=BG=2,
∵AD∥BC,
∴∠DAG=∠BMG,∠ADG=MBG,
∴△ADG∽△MBG,
∴,
∴GM?DG=AG?BG=4;
(2)如图,连接CG,
∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,
∴∠BAM=∠CPM,∠ABM=∠PCM,
∴△ABM∽△PCM,
同理,△ABG∽△PDG,
∵M为BC的中点,
∴BM=CM,S△BGM=S△CGM=,
∵△ABM∽△PCM,
∴=1,
∴AB=PC=CD,
∵△ABG∽△PDG,
∴=,
∴==2,
∴S△DGC=2S△BGC=3,
∵PC=DC,
∴S△DGC=S△PCG=3,
∴S△PDG=S△DGC+S△PCG=6,
故答案为:6.
3.解:(1)∵AD∥BC,DE∥AC,
∴四边形ACED是平行四边形,
∴AD=CE,
∵BC=CE,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴?ABCD是菱形;
(2)由(1)知,四边形ACED是平行四边形,
∴AC=DE,
∵OD=DE,
∴OD=AC,
∵四边形ABCD是菱形,
∴OA=OC=1,
∴OD=AC=2,
∵∠COD=90°,
∴CD===,
∴菱形ABCD的周长=4CD=4.
4.(1)证明:∵四边形ABCD是矩形,BD⊥EC,
∴∠DFE=∠DAB=90°,
∵∠FDE=∠ADB,
∴△FDE∽△ADB,
∴=,
∵∠EDB=∠FDA,
∴△AFD∽△BED;
(2)解:连接BE,
∵△AFD∽△BED,
∴∠DFA=∠DEB,
∴∠BEA=∠BFA,
∵AE=AB,∠DAB=90°,
∴∠BEA=45°,
∴∠BFA=45°,
∴∠DFG=∠BFA=45°;
(3)解:∵四边形ABCD是矩形,
∴AB=CD,∠CDE=∠DAB=90°,
∵BD⊥EC,
∴∠ADB=∠DCE,
∴△CDE∽△DAB,
∴=,
设AB的长为x,则DE=1﹣x,
∴=,
解得x1=,x2=(舍去),
∴AB的长为.
5.证明:(1)根据题意可知AB=CD=3,BC=AD=4,∠B=∠C=∠A=90°,
不妨设CN=x,则BN=4﹣x,
∵DN⊥MN,
∴∠MNB+∠DNC=90°,
又∠DNC+∠NDC=90°,
∴∠MNB=∠NDC,
∴△BMN∽△CND,
∴,即,
解得x=1或x=3,
∵CN<BN,
∴x=1,
∴CN=BM=1,BN=DC=3,DN==,MN==,
∴DN=MN;
(2)如下图,
过点D作DE=DN,并与BC的延长线交于点E,
则∠E=∠DNE,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC=60°,
∵AD∥BC,
∴∠ADC=∠DCE=60°,∠ADN=∠DNE,
∴∠B=DCE=∠DNM=60°,
∵∠BMN+∠MNB=120°,∠MNB+∠DNE=120°,
∴∠BMN=∠DNE,
∴∠BMN=∠E,
∴△BMN∽△CED,
∴
∴.
6.(1)证明:∵AD∥BC,MN∥AD,
∴MN∥BC,
∴△AME∽△ABC;
(2)证明:∵MN∥AD,AD∥BC,
∴=,
∵MN∥BC,
∴△AME∽△ABC,△DEN∽△DBC,
∴=,=,∴=,
∴ME=NE,
∴点E是MN的中点,ME=NE=MN,
∵AD∥BC∥MN,
∴△CEN∽△CAD,△AME∽△ABC,
∴=,=,
∴+=+==1,
∴+=1,
∴=+.
(3)结合(2)的结论,
∵AD=5,BC=7,
∴=,
∴ME=,
∵ME=NE,
∴MN=ME+NE=+=.
7.(1)证明:∵四边形EFGH为正方形,
∴GH∥EF.
∴GH∥BC,
∴△AHG∽△ABC.
解:(2)设AD与HG的交点为M,如图,
则AM是△AHG的高.
由(1)知:△AHG∽△ABC.
∴.
∵四边形EFGH为正方形,
∴HG=HE=FG,HG∥BC.
∵AD⊥BC,
∴MD=FG.
∴HG=MD.
设HG=MD=xcm,则AM=AD﹣MD=(20﹣x)cm,
∴.
解得:x=12,
∴正方形EFGH的边长为12cm.
∴正方形EFGH的面积为:12×12=144cm2
8.证明:(1)∵AG⊥BC,AF⊥DE于,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC
∴△AEF∽△ACG.
(2)由(1)知△AEF∽△ACG,
∴∠AEF=∠C
∵∠DAE=∠BAC(公共角),
∴△EAD∽△CAB.
∴∠ADE=∠B.
解:(3)由(2)知:△ADE∽△ABC,
∴.
由(1)知△AEF∽△ACG,
∴.
∴.
∵AD=3,AB=5,
∴.
9.解:(1)证明:∵AM=AB,AE⊥MB,
∴E为MB的中点,
∵∠AMB=45°,
∴∠MAB=180°﹣2×45°=90°,
∴AE=MB,
∵点O是BC的中点,
∴OE∥MC且OE=MC,
∴∠OEB=∠CMB=45°,
∴∠AEO=45°,
∵∠CMD=90°,
∴∠BMD=45°,
∴∠BMD=∠AEO,
∴△BMD∽△AEO;
(2)BD=AO;
证明:如图,作AF⊥MB于F,连接OF,
∵AM=AB,AF⊥MB,
∴F为MB的中点,
∵∠AMB=30°,
∴∠MAB=180°﹣2×30°=120°,
∴∠MCD=∠MAB=60°,
∵∠CMD=90°,
∴∠CDM=30°,
∴tanAMB=tan∠CDM=tan30°==,
∴MB=2AF,
∵点O是BC的中点,
∴OF∥MC且OF=MC,
∴∠OFB=∠CMB=30°,MD=2OF,
∴∠AFO=60°,
∴∠BMD=∠AFO,
∴△BMD∽△AFO,
∴BD=AO.
10.解:(1)∵∠AOD+∠BOC=180°,
∴∠AOB+∠DOC=180°;
∵∠OED=∠AOB,
∴∠OED+∠DOC=180°;
∵∠OED+∠EDO+∠DOE=180°,
∴∠CDO=∠COE,
又∵∠DCO=∠OCE,
∴△DCO∽△OCE(AAA),
∴,即OC2=DC?CE;
∵E为CD的中点,CD=4,
∴CE=2,则OC===.
(2)
将△AOB绕点O逆时针方向旋转,使得OB与OC重合,得ΔA'OC,
∴∠AOB=∠A'OC,OA'=OA,AB=A'C;
∵由(1)得∠AOB+∠DOC=180°,
∴∠A'OC+∠DOC=180°,
∴点D,O,A'在同一直线上;
∵OA=OD,
∴OD=OA',即点O是线段DA'的中点,
又∵E为CD的中点,
∴EO是△DA'C的中位线,
∴OE=CA'=AB.
11.解:(1)∵PQ∥AB,
∴∠B=∠CQP,∠C=∠C=90°,
∴△ABC∽△PQC;
(2)过D作DE⊥AC交AC于点E,DF⊥AB交AB于点F,作CG⊥AB交AB于点G、PQ于点H,
∵AB=13,BC=12,
∴AC=5,
由Rt△ABC面积=×BC×AC=×AB×CG,
∴CG=,
∵PQ∥AB,
∴DF=HG,
∴CH=﹣DF,
在Rt△CHP中,sin∠CPH=sin∠BAC,
∴=,
∴CP=5﹣DF,
∵AD平分∠BAC,
∴DF=DE,
在Rt△DEP中,tan∠DPE==,
∴EP=DF,
∵D是PQ的中点,DE∥BC,
∴CP=2EP=DF,
∴5﹣DF=DF,
∴DF=,
∴CP=,
∴AP=5﹣=.
12.解:(1)∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠CB=90°.
∴△ADC∽△ACB,
∴=,
∴AC2=AB?AD;
(2)∵△AFD∽△CFE.
∴,
∴AD∥CE,
∴∠DAC=∠ACE,
∵∠DAC=∠CAB,
∴∠CAB=∠ACE,
∴AE=CE,
∵∠CAB+∠B=∠ACE+∠BCE=90°,
∴∠BCE=∠B,
∴BE=CE,
∴AE=BE,
∴点E为AB的中点.
13.(1)证明:∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A,
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B﹣∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B,
∴△CDE∽△ACB;
(2)解:∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB=,
∴AB=2,
∵△CDE∽△ACB,
∴,
即,
解得CE=3,CE=﹣4(舍),
∴CE=3.
14.(1)证明:连接BD,
在△BAD中,AB⊥AD,AB=2,DA=1,
则BD==,
在△CBD中,BC2+BD2=()2+()2=10=()2=CD2,
∴∠CBD=90°,
∵BD=BC=,
∴△CBD是等腰直角三角形,
∴∠BCD=45°;
(2)解:作CM⊥AB,交AB的延长线于M,
∵∠ABD+∠ADB=90°,∠ABD+∠CBM=90°,
∴∠ADB=∠CBM,
∵∠DAB=∠BMC=90°,
∴△ABD∽△MCB(AA),
∴=,即=,
解得BM=1,
在△CMB中,CM==2,
∴AM=2+1=3,
在△CMA中,AC===.
15.(1)证明:∵AD⊥BC,DE⊥AC,
∴∠ADC=∠AED=90°,
∵∠DAE=∠CAD,
∴△ADE∽△ACD,
∴AD:AC=AE:AD,
∴AD2=AC?AE,
又∵AB=AC,
∴AD2=AB?AE;
(2)解:连接DF,如图所示:
由(1)得:AD2=AB?AE,
∴AD2=AB?AE=5×4=20,
∴AD=2,
∵AB=AC,AD⊥BC,
∴BD=CD,
∵F是AB的中点,
∴DF是△ABC的中位线,
∴DF=AC=,DF∥AC,
∴△DFG∽△AEG,
∴===,
∴=,
∴DG=AD=×2=.
16.解:(1)∵BD是△ABC的角平分线,
∴∠ABD=∠CBD.
∵AB=AE,
∴∠ABD=∠E.
∴∠E=∠CBD.
∵∠EDA=∠BDC,
∴△ADE∽△CDB.
(2)∵AE=AB,AB=6,
∴AE=6.
∵△ADE∽△CDB,
∴.
∵BD=4,DE=5,
∴.
∴BC=.
17.解:(1)∵DE∥BC,
∴∠AED=∠ECF,∠ADE=∠ABC,
又∵EF∥AB,
∴∠EFC=∠ABC(两直线平行,同位角也相等),
∴∠ADE=∠EFC,
∴△ADE∽△EFC(两角对应相等的两三角形相似);
(2)∵AB∥EF,DE∥BC,
∴四边形BDEF是平行四边形,
∴EF=BD,
∵=2,
∴=2,
又∵△ADE∽△EFC,
∴=()2=22=4(相似△的面积比等于相似比的平方),
∵△EFC的面积为1,
∴S△ADE=4.
18.(1)证明:∵AD⊥BC,
∠ADC=∠BDE=90°,
在△ACD和△BED中,
,
∴△ACD≌△BED(SAS),
∴∠EBD=∠CAD,
又∵∠BED=∠AEF,
∴△BED∽△AEF,
∴∠AFE=∠EDB=90°,
即BF⊥AC;
(2)证明:∵AG∥BC,
∴∠AGE=∠EDB,
由(1)知∠EBD=∠CAD,
∴∠AGE=∠CAD,
又∵∠AEG=∠BED=∠ACD,
∴△AEG∽△DCA,
∴=,
∴AE?AD=DC?AG,
∵DE2=AE?AD,DE=DC,
∴DC?AG=DE2=DC2,
∴DC=AG,
又∵AG∥DC,
∴四边形ADCG是平行四边形,
∵AD⊥BC,
∴四边形ADCG是矩形(有一个角是直角的平行四边形是矩形).
19.解:(1)∵△ADE∽△ACB,
∴∠ADE=∠ACB,
又∵AF为∠BAC的角平分线,
∴∠DAG=∠FAC,
∴在△ADG与△ACF中,
∴△ADG∽△ACF;
(2)∵ADE∽△ACB,
∴==,
在△ADG∽△ACF时,
AG:AF=AD:AC=2:3,
设AG为2x,则AF=3x,
即GF=x,
∴=.
20.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴△ABE∽△FDE.
∴.
∴ADE∽△GBE.
∴.
∴.
∴AE2=EF?EG.
(2)∵AB∥CD,
∴∠ABD=∠CDB.
∵∠ABD=∠AGD,
∴∠CDB=∠AGD.
∵∠DEF=∠GED,
∴△DEF∽GED.
∴.
∴DE2=EF?EG.
由(1)知:AE2=EF?EG.
∴DE=AE.
在△ABE和△DEG中,
.
∴△ABE≌△DEG(AAS).
∴AB=DG.
∵AD∥BG,
∴四边形ABGD是等腰梯形.
21.证明:(1)∵AC平分∠BCD,
∴∠DCA=∠ACB.
又∵AC⊥AB,AD⊥AE,
∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.
又∵E是BC的中点,
∴AE=BE,
∴∠EAB=∠ABC,
∴∠DAC=∠ABC,
∴△ACD∽△BCA,
∴=,
∴AC2=CD?BC;
(2)∵AC⊥AB,∠B=30°,E是BC的中点,
∴AC=BC=EB=EC,
∵EG⊥AB,∠B=30°,
∴EG=EB,
又∵EG=FG,
∴2EG=FE=EB,
∴EF=AC,
∵EG⊥AB,FG=EG,
∴AF=AE=EB,
∴AF=FE=EC=CA,
∴四边形AFEC是菱形.
22.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ADF∽△EAB;
(2)解:∵BC=AD=10,E是BC边的中点,
∴BE=5,
∴AE===13,
由(1)得:△ADF∽△EAB,
∴=,
即=,
解得:DF=.
23.解:(1)AE=CD,
如图1,在BC上取一点G,使AD=BG,连接DG,
∵∠BAC=45°,∠ACB=90°,
∴△ACB是等腰直角三角形,
∴AC=BC,
∴AC﹣CD=BC﹣BG,
即CD=CG,
∴△CDG是等腰直角三角形,
∴DG=CD,∠DGC=45°,
∴∠DGB=135°,
∵AP⊥AB,
∴∠BAP=90°,
∵∠DAE=90°+45°=135°,
∴∠DAE=∠DGB,
∵DE⊥DB,
∴∠EDB=90°,
∴∠EDA+∠BDC=90°,
∵∠BDC+∠DBC=90°,
∴∠EDA=∠DBC,
∴△EAD≌△DGB(ASA),
∴AE=DG,
∴AE=CD;
(2)AE=2CD,理由是
如图2,
过D作DF∥AB,交BC于F,
则∠FDC=∠BAC=30°,,
∴,
∵AP⊥AB,DE⊥BD,
∴∠BAP=∠BDE=90°,
∵∠ADE+∠BDE+∠BDC=180°,
∴∠ADE+∠BDC=90°,
∵∠ACB=90°,∠FDC=30°
∴∠DBC+∠BDC=90°,CF=DF,
∴∠ADE=∠DBC,
∵∠DAE=∠BAC+∠BAP,∠BFD=∠FDC+∠ACB,
∴∠DAE=∠DBC,
∴△DAE∽△BFD,
∴,
∴,
∴,
∴=2,即AE=2CD;
(3)CD=AE?sinα,理由是
如图3,
过D作DF∥AB,交BC于F,
则∠FDC=∠BAC=α,,
∴,
∵AP⊥AB,DE⊥BD,
∴∠BAP=∠BDE=90°,
∵∠ADE+∠BDE+∠BDC=180°,
∴∠ADE+∠BDC=90°,
∵∠ACB=90°,∠FDC=α
∴∠DBC+∠BDC=90°,sin∠FDC=sinα=,
∴∠ADE=∠DBC,
∵∠DAE=∠BAC+∠BAP,∠BFD=∠FDC+∠ACB,
∴∠DAE=∠BFD,
∴△DAE∽△BFD,
∴,
∴,
∴=sinα,
∴CD=AE?sinα.
24.解:(1)证明:如图,
∵BD平分∠ABC,
∴∠ABF=∠EBF,
∵BA=BE,BF=BF,
∴△ABF≌△EBF(SAS),
∴AF=EF,
同理可得△ABD≌△EBD(SAS),
∴AD=ED,∠ADB=∠EDB,
∵AG∥DE,
∴∠AFD=∠EDF,
∴∠AFD=∠ADF,
∴AF=AD,
∴AF=FE=ED=DA,
∴四边形AFED是菱形.
(2)证明:由(1)得△ABF≌△EBF,
∴∠BAG=∠BEF,
∵四边形AFED是菱形,
∴AD∥FE,
∴∠BEF=∠C,
∴∠BAG=∠C,
∵∠ABG=∠CBA,
∴△ABG∽△CBA,
∴,即AB2=BG?BC.
(3)由(2)得,△ABG∽△CBA,AB=AC,
∴AG=BG,
∴∠GAB=∠GBA,
∴∠AGC=2∠GAB,
∵BG=CE,
∴BE=CG,
∴CG=CA,
∴∠CAG=∠CGA,
∵∠CAG=2∠DAE,
∴∠DAE=∠ABC,
∴∠DEA=∠ACB,
∴△DAE∽△ABC,
∴=()2,
∵AB2=BG?BC,AB=BE,BG=EC,
∴BE2=EC?BC,
∴点E是BC的黄金分割点,
∴=,
∴=,
∵∠EAC=∠C,
∴CE=AE,
∴=,
∴=.
25.解:(1)证明:∵BF⊥DE,
∴∠BFD=90°,
在Rt△BEF中,sin∠EBF=,
在Rt△DBF中,sin∠BDE=,
∵EF?BD=BE?BF,
∴=,
∴sin∠EBF=sin∠BDE,
∴∠EBF=∠BDE,
∵正方形ABCD,
∴∠DAE=90°=∠BFD,
∴∠EBF+∠BEF=∠ADE+∠AED=90°,
∵∠BEF=∠AED,
∴∠EBF=∠ADE,
∴∠ADE=∠BDE;
(2)证明:如图,延长BF交DA的延长线于H,
∵∠ADE=∠BDE,∠DFH=∠DFB=90°,DF=DF,
∴△DFH≌△DFB(ASA),
∴HF=BF,
∵正方形ABCD,
∴AD∥BC,AD=AB=BC,
∴∠G=∠ADE,∠GBF=∠H,
在△GBF和△DHF中,
,
∴△GBF≌△DHF(AAS),
∴BG=DH=AD+AH=BC+AH,
在△DAE和△BAH中,
,
∴△DAE≌△BAH(ASA),
∴AH=AE,
∴BG=BC+AE.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,AD∥BC,
∵AE平分∠BAD,
∴∠BAF=∠DAF=∠F,
∴AD=DF,
∵∠GDF=∠F,
∴△GDF∽△DAF,
∴=,
∴AD2=DG?AF;
(2)解:∵AF平分∠BAD,
∴∠BAE=∠DAF,
∵AD∥BC,
∴∠BEA=∠DAF,
∴∠BEA=∠BAE,
∵BG⊥AE,AB=6,AD=9,
∴BA=BE=6,
∵∠BEA=∠CEF,
∴∠CEF=∠F,
∴EC=CF=3,DF=AD=9,
∴==,
即AG=GE=EF,
∵AD2=DG?AF,
∴AF2=81,
∴AF=.
27.解:(1)∵AD为∠BAC的平分线,
∴∠BAD=∠DAC,
∵∠EFD=∠BDF,
∴180°﹣∠EFD=180°﹣∠BDF,
∴∠AFE=∠ADC,
∴△AFE∽△ADC;
(2)由(1)得,△AFE∽△ADC,
∴∠AEF=∠C,
∵∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∵=,△AFE∽△ADC,
∴,
∴,
∵=2,AE=AF,
∴,
∴EB=2FD.
28.证明:(1)∵四边形ABCD是平行四边形.
∴AD∥BC.
∴∠ADE=∠E.
∵∠ADE=∠BAC.
∴∠BAC=∠E.
∵∠ACB=∠ECF.
∴△ACB∽△ECF.
∴.
∴CF?CA=CB?CE
(2)由(1)知∠ADE=∠E.
∵∠ADF=∠CFE.
∴△ADF∽△CEF.
∴.
∴.
∵AC=DE.
∴EF=CF.
∵△ACB∽△ECF.
∴AB=BC
∵四边形ABCD是平行四边形.
∴四边形ABCD是菱形.
29.(1)证明:∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A,
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B﹣∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B,
∴△CDE∽△ABC,
(2)解:令EA=k,DA=,CE=x,
∵△CDE∽△ABC,
∴,
即,
解得x=3k,x=﹣4k(舍),
所以.
30.解:(1)∵将△ADE绕点A顺时针旋转90°得△ABF,
∴∠DAE=∠BAF,AE=AF,
∴△AEF是等腰直角三角形,
∴∠AFE=45°,
∵AE平分∠DAC,
∴∠DAE=∠EAC,
∴∠FAB=∠CAE,
在正方形ABCD中,∠ACD=45°,
∴∠ACD=∠AFE,
∴△AFG∽△ACE,
(2)过F作BC平行线交AB,CD于G,H,
∴△AGF∽△FHE,
∵,
设FH=x,
则AG=2x,GF=4﹣x,EH=,
∵AG=DH,
∴2x=2+,
解得x=,
∴AG=,GF=4﹣=,
∴BG=4﹣=,
在Rt△BGF中,BF=.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
