13.3全等三角形的判定 同步能力提升训练 2021-2022学年冀教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 13.3全等三角形的判定 同步能力提升训练 2021-2022学年冀教版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 13:22:24 | ||
图片预览



文档简介
2021-2022学年冀教版八年级数学上册《13.3全等三角形的判定》
同步能力提升训练(附答案)
一.选择题
1.如图,∠C=∠D,∠ABC=∠BAD,证明△ABC≌△BAD的判定定理( )
A.SSS
B.SAS
C.AAS
D.HL
2.在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是( )
A.0<AD<12
B.1<AD<6
C.0<AD<6
D.2<AD<12
3.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=EC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
4.如图,直线EF经过AC中点O,交AB于点E,交CD于点F,下列能使△AOE≌△COF的条件有( )①∠A=∠C;②AB∥CD;③AE=CF;④OE=OF.
A.1个
B.2个
C.3个
D.4个
5.如图,AB=14,AC=6,AC⊥AB,BD⊥AB,垂足分别为A、B.点P从点A出发,以每秒2个单位的速度沿AB向点B运动;点Q从点B出发,以每秒a个单位的速度沿射线BD方向运动.点P、点Q同时出发,当以P、B、Q为顶点的三角形与△CAP全等时,a的值为( )
A.2
B.3
C.2或3
D.2或
6.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20°
B.40°
C.60°
D.70°
二.填空题
7.如图,在△ABC和△ADE中,∠BAC=∠DAE,BC=DE,请你添加一个条件
,使△ABC≌△ADE(填一个即可).
8.如图,在△ABC和△EBD中,AB=EB,AC=ED,若再添加一个条件,则下列条件中能使得△ABC与△EBD全等的有
.
①BC=BD;②∠C=∠D;③∠A=∠E;④∠ABC=∠DBE=90°.
9.如图,在△ABC中,AB=AC,D为线段BC上一动点(不与点B、C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接CE,当CE∥AB,∠BAD=36°时,∠DEC=
度.
10.如图,在△ACD与△BCE中,AD与BE相交于点P,若AC=BC,AD=BE,CD=CE,∠DCE=55°,则∠APB的度数为
.
11.如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=
cm.
三.解答题
12.如图,点A,D,B在同一直线上,AC=BD,AB=DE,∠C=∠DFB.试说明:△DEB≌△ABC.
13.如图,CB为∠ACE的角平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
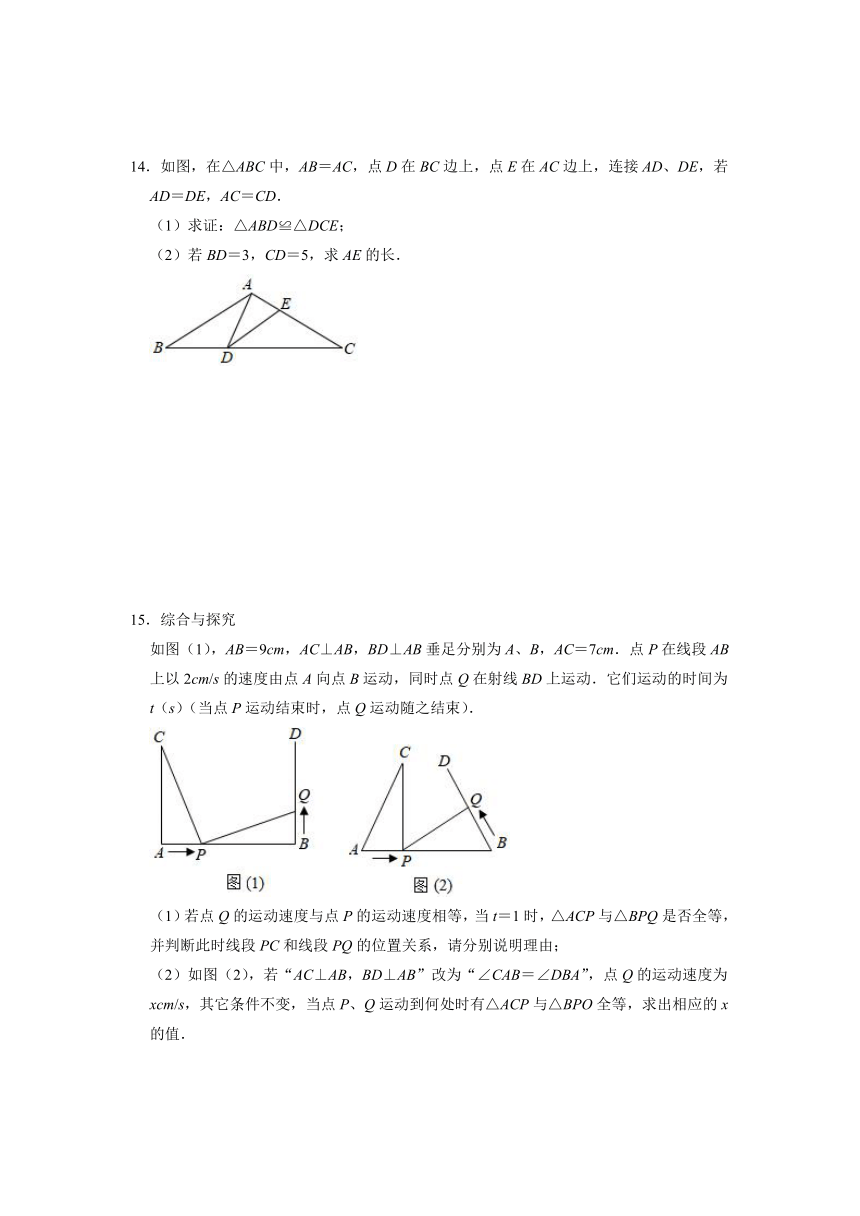
14.如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连接AD、DE,若AD=DE,AC=CD.
(1)求证:△ABD≌△DCE;
(2)若BD=3,CD=5,求AE的长.
15.综合与探究
如图(1),AB=9cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=7cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点Q的运动速度为xcm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPO全等,求出相应的x的值.
16.如图,若AB∥CD,AB=CD且CE=BF.
(1)求证:AE=DF;
(2)若∠AEB=62°,∠C=47°,求∠A的度数.
17.如图所示,在△ABC中,AD是∠BAC的平分线,M是BC的中点,MF∥DA交BA的延长线于点E,交AC于点F,求证:BE=CF.
18.如图,△ABC中,AB=AC,点E,F在边BC上;BE=CF.
(1)求证:△ABE≌△ACF;
(2)若点D在AF的延长线上,AD=AC,∠BAE=30°,∠BAD=75°,求证:AB∥DC.
19.在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AC上,且AD=6cm,过点A作射线AE⊥AC(AE与BC在AC同侧),若动点P从点A出发,沿射线AE匀速运动,运动速度为1cm/s,设点P运动时间为t秒.连接PD、BD.
(1)如图①,当PD⊥BD时,求证:△PDA≌△DBC;
(2)如图②,当PD⊥AB于点F时,求此时t的值.
20.如图,四边形ABCD中,AD∥BC,E为CD的中点,连结BE并延长交AD的延长线于点F.
(1)求证:△BCE≌△FDE;
(2)连结AE,当AE⊥BF,BC=2,AD=1时,求AB的长.
参考答案
1.解:在△ABC和△BAD中,
,
∴△ABC≌△BAD(AAS).
故选:C.
2.解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7﹣5<AE<7+5,
即7﹣5<2AD<7+5,
∴1<AD<6.
故选:B.
3.解:A.AB=DE,BC=EC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,BC=EC,AB=DE,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
所以∠B=∠E,∠ACB=∠DCE,AB=DE,符合全等三角形的判定定理AAS,能推出△ABC≌△DEC,故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
4.解:∵O点为AC的中点,
∴OA=OC,
∵∠AOE=∠COF,
∴当①∠A=∠C,可根据“ASA“判断△AOE≌△COF;
当②AB∥CD,则∠A=∠C,可根据“ASA“判断△AOE≌△COF;
当④OE=OF,则可根据“SAS“判断△AOE≌△COF.
故选:C.
5.解:当△CAP≌△PBQ时,则AC=PB,AP=BQ,
∵AC=6,AB=14,
∴PB=6,AP=AB﹣AP=14﹣6=8,
∴BQ=8,
∴8÷a=8÷2,
解得a=2;
当△CAP≌△QBP时,则AC=BQ,AP=BP,.
∵AC=6,AB=14,
∴BQ=6,AP=BP=7,
∴6÷a=7÷2,
解得a=;
由上可得a的值是2或,
故选:D.
6.解:∵BD是高,∠CBD=20°,
∴∠BCD=180°﹣90°﹣20°=70°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL),
∴∠BCD=∠CBE=70°,
∴∠A=180°﹣70°﹣70°=40°.
故选:B.
7.解:∵∠BAD=∠CAE,BC=DE,
添加∠B=∠D,利用AAS得出△ABC≌△ADE;
添加∠ACB=∠AED,利用AAS得出△ABC≌△ADE;
故答案为:∠B=∠D或∠ACB=∠AED.
8.解:∵AB=EB,AC=ED,
∴当BC=BD时,可根据“SSS”可证△ABC≌△EBD;
当∠C=∠D时,无法证明△ABC≌△EBD;
当∠A=∠E时,可根据“SAS”可证△ABC≌△EBD;
当∠ABC=∠DBE=90°,可根据“HL”可证△ABC≌△EBD;
故答案为①③④.
9.解:∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠BAC=∠B,
∴AC=BC,
∴△ABC是等边三角形,
∴∠BAC=∠DAE=∠ACB=∠ACE=60°,
∴△DAE是等边三角形,
∴∠AED=60°,
∴∠DEC=180°﹣36°﹣60°﹣60°=24°,
故答案为:24.
10.解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠D=∠E,
∵∠DPE+∠1+∠E=∠DCE+∠2+∠D,
而∠1=∠2,
∴∠DPE=∠DCE=55°,
∴∠APB=∠DPE=55°.
故答案为55°.
11.解:∵CF∥AB,
∴∠AED=∠F,∠FCD=∠A.
∵点D为AC的中点,
∴AD=CD.
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS).
∴AE=CF,
∵AB=15cm,CF=10cm,
∴BE=AB﹣AE=AB﹣CF=15﹣10=5(cm).
故答案为5.
12.证明:∵∠C=∠DFB,
∴AC∥DE,
∴∠A=∠BDE,
在△ABC与△DEB中,
,
∴△ABC≌△DEB(SAS).
13.证明:(1)∵CB为∠ACE的角平分线,
∴∠ACB=∠FCE,
在△ABC与△FEC中,
,
∴△ABC≌△FEC(AAS),
∴AB=FE;
(2)∵AB∥CE,
∴∠B=∠FCE,
∴∠E=∠B=∠FCE=∠ACB,
∵ED⊥AC,即∠CDE=90°,
∴∠E+∠FCE+∠ACB=90°,
即3∠ACB=90°,
∴∠ACB=30°,
∴∠B=30°,
∴∠A=180°﹣∠B﹣∠ACB=180°﹣30°﹣30°=120°.
14.证明:∵AB=AC,
∴∠B=∠C,
又∠1=∠2,AD=DE,
在△ABD与△DCE中,
,
∴△ABD≌△DCE(AAS);
(2)解:∵△ABD≌△DCE,
∴AB=DC=5,CE=BD=3,
∵AC=AB,
∴AC=5,
∴AE=AB﹣EC=5﹣3=2.
15.解:(1)△ACP?△BPO,PC⊥PO.
理由:∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
∵AP=BQ=2,
∴BP=7,
∴BP=AC,
在△ACP和△BPQ中,
,
∴△ACP?△BPQ(SAS),
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)①若△ACP?△BPQ,
则AC=BP,AP=BQ,
可得:7=9﹣2t,2t=xt,
解得:x=2,t=1;
②若△ACP?△BOP,
则AC=BQ,AP=BP,可得:7=xt,2t=9﹣2t
解得:,.
综上所述,当△ACP与△BPQ全等时x的值为2或.
16.(1)证明:∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CF=BE,
在△CDF和△BAE中,
∴△CDF≌△BAE(SAS),
∴AE=DF;
(2)解:∵△CDF≌△BAE,
∴∠C=∠B=47°,
∵∠AEB=62°,
∴∠A=180°﹣∠AEB﹣∠B=180°﹣62°﹣47°=71°.
17.证明:如图,过点B作BN∥AC交EM的延长线于N,
∴∠MBN=∠C,∠N=∠MFC,
∵M为BC的中点,
∴BM=CM,
在△BMN和△CMF中,
,
∴△BMN≌△CMF(AAS),
∴BN=CF,
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵ME∥AD,
∴∠E=∠BAD,∠MFC=∠CAD,
∴∠E=∠MFC,
∴∠E=∠N,
∴BE=BN,
∴BE=CF.
18.证明:∵AB=AC,
∴∠B=∠ACF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS);
(2)∵△ABE≌△ACF,∠BAE=30°,
∴∠BAE=∠CAF=30°,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ADC==75°,
∵∠BAD=75°,
∴∠BAD=∠ADC,
∴AB∥DC.
19.(1)证明:如图①,∵PD⊥BD,
∴∠PDB=90°,
∴∠BDC+∠PDA=90°,
又∵∠C=90°,
∴∠BDC+∠CBD=90°,
∴∠PDA=∠CBD,
又∵AE⊥AC,
∴∠PAD=90°,
∴∠PAD=∠C=90°,
又∵BC=6cm,AD=6cm,
∴AD=BC,
在△PAD和△DCB中,
,
∴△PDA≌△DBC(ASA);
(2)解:如图②,∵PD⊥AB,
∴∠AFD=∠AFP=90°,
∴∠PAF+∠APF=90°,
又∵AE⊥AC,
∴∠PAF+∠CAB=90°,
∴∠APF=∠CAB,
在△APD和△CAB中,
,
∴△APD≌△CAB(AAS),
∴AP=AC,
∵AC=8cm,
∴AP=8cm,
∴t=8.
20.解:(1)∵AD∥BC,
∴∠F=∠EBC,∠FDE=∠C,
∵点E为CD的中点,
∴ED=EC,
在△FDE和△BEC中,
,
∴△FDE≌△BEC(AAS);
(2)∵△FDE≌△BEC,
∴BE=EF,BC=DF,
∵AE⊥BF,
∴AB=AF,
∴AB=AF=AD+DF=AD+BC=1+2=3,
∴AB的长为3.
同步能力提升训练(附答案)
一.选择题
1.如图,∠C=∠D,∠ABC=∠BAD,证明△ABC≌△BAD的判定定理( )
A.SSS
B.SAS
C.AAS
D.HL
2.在△ABC中,AB=5,AC=7,AD是BC边上的中线,则AD的取值范围是( )
A.0<AD<12
B.1<AD<6
C.0<AD<6
D.2<AD<12
3.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=EC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
4.如图,直线EF经过AC中点O,交AB于点E,交CD于点F,下列能使△AOE≌△COF的条件有( )①∠A=∠C;②AB∥CD;③AE=CF;④OE=OF.
A.1个
B.2个
C.3个
D.4个
5.如图,AB=14,AC=6,AC⊥AB,BD⊥AB,垂足分别为A、B.点P从点A出发,以每秒2个单位的速度沿AB向点B运动;点Q从点B出发,以每秒a个单位的速度沿射线BD方向运动.点P、点Q同时出发,当以P、B、Q为顶点的三角形与△CAP全等时,a的值为( )
A.2
B.3
C.2或3
D.2或
6.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20°
B.40°
C.60°
D.70°
二.填空题
7.如图,在△ABC和△ADE中,∠BAC=∠DAE,BC=DE,请你添加一个条件
,使△ABC≌△ADE(填一个即可).
8.如图,在△ABC和△EBD中,AB=EB,AC=ED,若再添加一个条件,则下列条件中能使得△ABC与△EBD全等的有
.
①BC=BD;②∠C=∠D;③∠A=∠E;④∠ABC=∠DBE=90°.
9.如图,在△ABC中,AB=AC,D为线段BC上一动点(不与点B、C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接CE,当CE∥AB,∠BAD=36°时,∠DEC=
度.
10.如图,在△ACD与△BCE中,AD与BE相交于点P,若AC=BC,AD=BE,CD=CE,∠DCE=55°,则∠APB的度数为
.
11.如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=
cm.
三.解答题
12.如图,点A,D,B在同一直线上,AC=BD,AB=DE,∠C=∠DFB.试说明:△DEB≌△ABC.
13.如图,CB为∠ACE的角平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB∥CE,求∠A的度数.
14.如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连接AD、DE,若AD=DE,AC=CD.
(1)求证:△ABD≌△DCE;
(2)若BD=3,CD=5,求AE的长.
15.综合与探究
如图(1),AB=9cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=7cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点Q的运动速度为xcm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPO全等,求出相应的x的值.
16.如图,若AB∥CD,AB=CD且CE=BF.
(1)求证:AE=DF;
(2)若∠AEB=62°,∠C=47°,求∠A的度数.
17.如图所示,在△ABC中,AD是∠BAC的平分线,M是BC的中点,MF∥DA交BA的延长线于点E,交AC于点F,求证:BE=CF.
18.如图,△ABC中,AB=AC,点E,F在边BC上;BE=CF.
(1)求证:△ABE≌△ACF;
(2)若点D在AF的延长线上,AD=AC,∠BAE=30°,∠BAD=75°,求证:AB∥DC.
19.在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AC上,且AD=6cm,过点A作射线AE⊥AC(AE与BC在AC同侧),若动点P从点A出发,沿射线AE匀速运动,运动速度为1cm/s,设点P运动时间为t秒.连接PD、BD.
(1)如图①,当PD⊥BD时,求证:△PDA≌△DBC;
(2)如图②,当PD⊥AB于点F时,求此时t的值.
20.如图,四边形ABCD中,AD∥BC,E为CD的中点,连结BE并延长交AD的延长线于点F.
(1)求证:△BCE≌△FDE;
(2)连结AE,当AE⊥BF,BC=2,AD=1时,求AB的长.
参考答案
1.解:在△ABC和△BAD中,
,
∴△ABC≌△BAD(AAS).
故选:C.
2.解:如图,延长中线AD到E,使DE=AD,
∵AD是三角形的中线,
∴BD=CD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE,
∵AB=5,BE=AC=7,
∴7﹣5<AE<7+5,
即7﹣5<2AD<7+5,
∴1<AD<6.
故选:B.
3.解:A.AB=DE,BC=EC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,BC=EC,AB=DE,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
所以∠B=∠E,∠ACB=∠DCE,AB=DE,符合全等三角形的判定定理AAS,能推出△ABC≌△DEC,故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
4.解:∵O点为AC的中点,
∴OA=OC,
∵∠AOE=∠COF,
∴当①∠A=∠C,可根据“ASA“判断△AOE≌△COF;
当②AB∥CD,则∠A=∠C,可根据“ASA“判断△AOE≌△COF;
当④OE=OF,则可根据“SAS“判断△AOE≌△COF.
故选:C.
5.解:当△CAP≌△PBQ时,则AC=PB,AP=BQ,
∵AC=6,AB=14,
∴PB=6,AP=AB﹣AP=14﹣6=8,
∴BQ=8,
∴8÷a=8÷2,
解得a=2;
当△CAP≌△QBP时,则AC=BQ,AP=BP,.
∵AC=6,AB=14,
∴BQ=6,AP=BP=7,
∴6÷a=7÷2,
解得a=;
由上可得a的值是2或,
故选:D.
6.解:∵BD是高,∠CBD=20°,
∴∠BCD=180°﹣90°﹣20°=70°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL),
∴∠BCD=∠CBE=70°,
∴∠A=180°﹣70°﹣70°=40°.
故选:B.
7.解:∵∠BAD=∠CAE,BC=DE,
添加∠B=∠D,利用AAS得出△ABC≌△ADE;
添加∠ACB=∠AED,利用AAS得出△ABC≌△ADE;
故答案为:∠B=∠D或∠ACB=∠AED.
8.解:∵AB=EB,AC=ED,
∴当BC=BD时,可根据“SSS”可证△ABC≌△EBD;
当∠C=∠D时,无法证明△ABC≌△EBD;
当∠A=∠E时,可根据“SAS”可证△ABC≌△EBD;
当∠ABC=∠DBE=90°,可根据“HL”可证△ABC≌△EBD;
故答案为①③④.
9.解:∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠BAC=∠B,
∴AC=BC,
∴△ABC是等边三角形,
∴∠BAC=∠DAE=∠ACB=∠ACE=60°,
∴△DAE是等边三角形,
∴∠AED=60°,
∴∠DEC=180°﹣36°﹣60°﹣60°=24°,
故答案为:24.
10.解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠D=∠E,
∵∠DPE+∠1+∠E=∠DCE+∠2+∠D,
而∠1=∠2,
∴∠DPE=∠DCE=55°,
∴∠APB=∠DPE=55°.
故答案为55°.
11.解:∵CF∥AB,
∴∠AED=∠F,∠FCD=∠A.
∵点D为AC的中点,
∴AD=CD.
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS).
∴AE=CF,
∵AB=15cm,CF=10cm,
∴BE=AB﹣AE=AB﹣CF=15﹣10=5(cm).
故答案为5.
12.证明:∵∠C=∠DFB,
∴AC∥DE,
∴∠A=∠BDE,
在△ABC与△DEB中,
,
∴△ABC≌△DEB(SAS).
13.证明:(1)∵CB为∠ACE的角平分线,
∴∠ACB=∠FCE,
在△ABC与△FEC中,
,
∴△ABC≌△FEC(AAS),
∴AB=FE;
(2)∵AB∥CE,
∴∠B=∠FCE,
∴∠E=∠B=∠FCE=∠ACB,
∵ED⊥AC,即∠CDE=90°,
∴∠E+∠FCE+∠ACB=90°,
即3∠ACB=90°,
∴∠ACB=30°,
∴∠B=30°,
∴∠A=180°﹣∠B﹣∠ACB=180°﹣30°﹣30°=120°.
14.证明:∵AB=AC,
∴∠B=∠C,
又∠1=∠2,AD=DE,
在△ABD与△DCE中,
,
∴△ABD≌△DCE(AAS);
(2)解:∵△ABD≌△DCE,
∴AB=DC=5,CE=BD=3,
∵AC=AB,
∴AC=5,
∴AE=AB﹣EC=5﹣3=2.
15.解:(1)△ACP?△BPO,PC⊥PO.
理由:∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
∵AP=BQ=2,
∴BP=7,
∴BP=AC,
在△ACP和△BPQ中,
,
∴△ACP?△BPQ(SAS),
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)①若△ACP?△BPQ,
则AC=BP,AP=BQ,
可得:7=9﹣2t,2t=xt,
解得:x=2,t=1;
②若△ACP?△BOP,
则AC=BQ,AP=BP,可得:7=xt,2t=9﹣2t
解得:,.
综上所述,当△ACP与△BPQ全等时x的值为2或.
16.(1)证明:∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CF=BE,
在△CDF和△BAE中,
∴△CDF≌△BAE(SAS),
∴AE=DF;
(2)解:∵△CDF≌△BAE,
∴∠C=∠B=47°,
∵∠AEB=62°,
∴∠A=180°﹣∠AEB﹣∠B=180°﹣62°﹣47°=71°.
17.证明:如图,过点B作BN∥AC交EM的延长线于N,
∴∠MBN=∠C,∠N=∠MFC,
∵M为BC的中点,
∴BM=CM,
在△BMN和△CMF中,
,
∴△BMN≌△CMF(AAS),
∴BN=CF,
∵AD为∠BAC的角平分线,
∴∠BAD=∠CAD,
∵ME∥AD,
∴∠E=∠BAD,∠MFC=∠CAD,
∴∠E=∠MFC,
∴∠E=∠N,
∴BE=BN,
∴BE=CF.
18.证明:∵AB=AC,
∴∠B=∠ACF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS);
(2)∵△ABE≌△ACF,∠BAE=30°,
∴∠BAE=∠CAF=30°,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ADC==75°,
∵∠BAD=75°,
∴∠BAD=∠ADC,
∴AB∥DC.
19.(1)证明:如图①,∵PD⊥BD,
∴∠PDB=90°,
∴∠BDC+∠PDA=90°,
又∵∠C=90°,
∴∠BDC+∠CBD=90°,
∴∠PDA=∠CBD,
又∵AE⊥AC,
∴∠PAD=90°,
∴∠PAD=∠C=90°,
又∵BC=6cm,AD=6cm,
∴AD=BC,
在△PAD和△DCB中,
,
∴△PDA≌△DBC(ASA);
(2)解:如图②,∵PD⊥AB,
∴∠AFD=∠AFP=90°,
∴∠PAF+∠APF=90°,
又∵AE⊥AC,
∴∠PAF+∠CAB=90°,
∴∠APF=∠CAB,
在△APD和△CAB中,
,
∴△APD≌△CAB(AAS),
∴AP=AC,
∵AC=8cm,
∴AP=8cm,
∴t=8.
20.解:(1)∵AD∥BC,
∴∠F=∠EBC,∠FDE=∠C,
∵点E为CD的中点,
∴ED=EC,
在△FDE和△BEC中,
,
∴△FDE≌△BEC(AAS);
(2)∵△FDE≌△BEC,
∴BE=EF,BC=DF,
∵AE⊥BF,
∴AB=AF,
∴AB=AF=AD+DF=AD+BC=1+2=3,
∴AB的长为3.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
