2021—2022学年冀教版八年级数学上册16.1轴对称分层训练 (word解析版)
文档属性
| 名称 | 2021—2022学年冀教版八年级数学上册16.1轴对称分层训练 (word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 311.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 15:29:32 | ||
图片预览




文档简介
16.1 轴对称
【基础练习】
知识点
1 轴对称图形
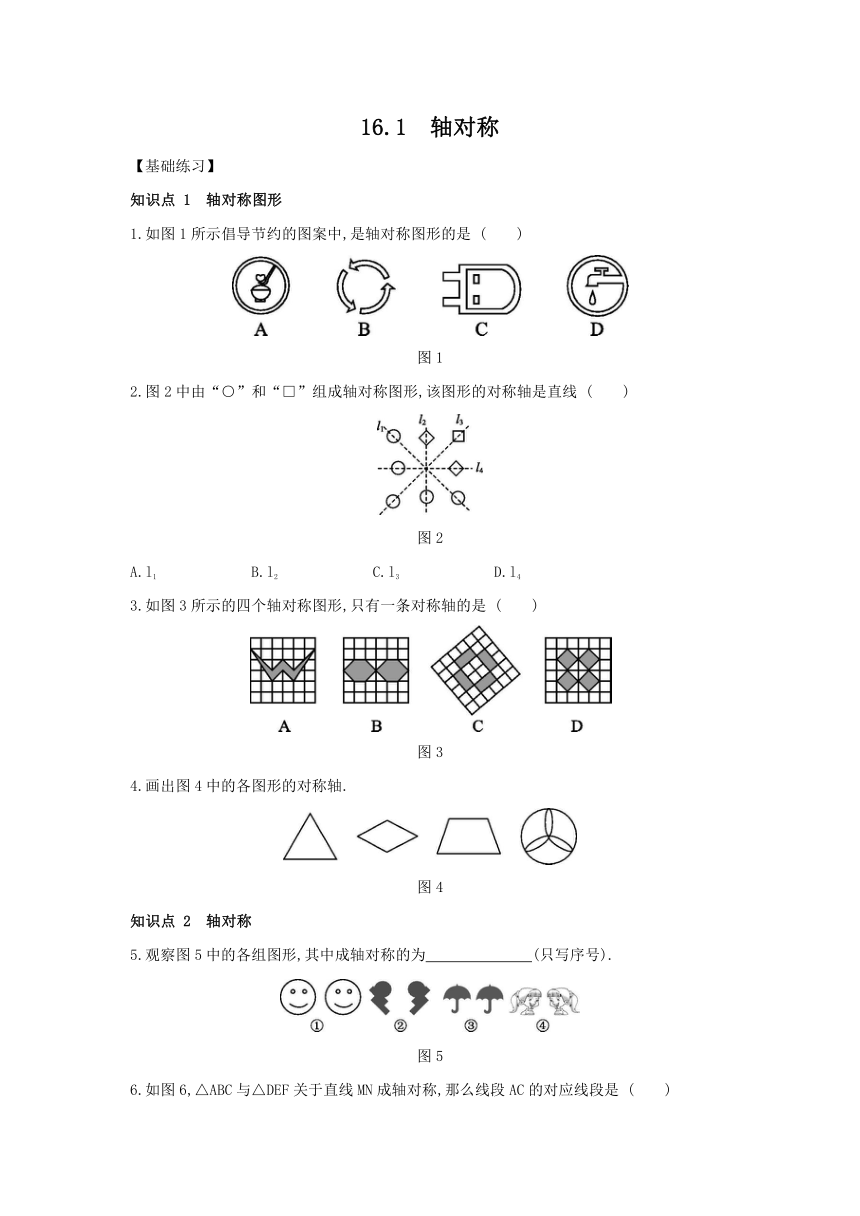
1.如图1所示倡导节约的图案中,是轴对称图形的是
( )
图1
2.图2中由“○”和“□”组成轴对称图形,该图形的对称轴是直线
( )
图2
A.l1
B.l2
C.l3
D.l4
3.如图3所示的四个轴对称图形,只有一条对称轴的是
( )
图3
4.画出图4中的各图形的对称轴.
图4
知识点
2 轴对称
5.观察图5中的各组图形,其中成轴对称的为 (只写序号).?
图5
6.如图6,△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是
( )
图6
A.AB
B.DF
C.DE
D.EF
知识点
3 轴对称的性质
7.下列说法中,正确的是
( )
A.
两个全等的三角形一定关于某条直线对称
B.两个图形关于某条直线对称,对应点一定在直线两旁
C.成轴对称的两个图形对应点连线的垂线,就是它们的对称轴
D.关于某条直线对称的两个三角形是全等三角形
8.如图7,直线MN是四边形AMBN的对称轴,与对角线AB交于点Q,P是直线MN上一点,下列判断错误的是
( )
图7
A.AQ=BQ
C.∠MAP=∠MBP
B.AP=BP
D.∠ANM=∠NMB
9.如图8,已知△ABC和△A'B'C'关于直线l成轴对称.
(1)在图中标出点A,B,C的对应点A',B',C';
(2)若AB=5,则对应线段A'B'= ;?
(3)若∠A=50°,∠C'=20°,求∠B的度数.
图8
知识点
4 利用轴对称的性质作图
10.如图9,用三角尺画出△ABC关于直线MN的对称图形.(不写作法,保留作图痕迹)
图9
【能力提升】
11.将一张长方形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可能见到的图形是
( )
图10
12.如图11所示,把一张长方形纸片沿EF折叠后,点D,C分别落在点D',C'的位置.若∠EFB=65°,则∠AED'等于
( )
图11
A.70°
B.65°
C.50°
D.25°
13.如图12,在由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有
( )
图12
A.1个
B.2个
C.3个
D.4个
14.如图13,△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,OC与BD交于点E.若∠C=15°,∠D=25°,则∠BEC的度数为
.?
图13
15.如图14,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为 .?
图14
16.如图15,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB的对称点是D,连接CD交OA于点M,交OB于点N.
(1)①若∠AOB=60°,则∠COD= °;?
②若∠AOB=α,求∠COD的度数.
(2)若CD=4,则△PMN的周长为 .?
图15
17.在如图16所示的网格中,每个小正方形的边长均为1.认真观察图中阴影部分构成的图案,回答下列问题:
图16
(1)请写出四个图案都具有的两个共同特征.
特征1:
;?
特征2:
.?
(2)请在备用图中设计出你心中最美丽的图案,使它也具备你在(1)中写出的特征.
16.1 轴对称
1.C [解析]
根据轴对称图形的定义可以发现A,B,D都不是轴对称图形,只有C符合要求.
2.C
3.A [解析]
A中的图案只有1条对称轴;B中的图案有2条对称轴;C中的图案有4条对称轴;D中的图案有4条对称轴.
4.解:如图.
5.①②④ [解析]
③中的伞把部分不对称,故填①②④.
6.B [解析]
△ABC与△DEF关于直线MN成轴对称,线段AC的对应线段是DF.
7.D [解析]
根据轴对称的性质可知:A项,两个三角形全等,它们不一定关于某条直线对称,故本选项错误.B项,两个图形关于某条直线对称,对应点不一定在直线两旁,还有可能在直线上,故本选项错误.C项,成轴对称的两个图形的对应点连线的垂直平分线,就是它们的对称轴,故本选项错误.D项,两个关于某条直线对称的三角形是全等三角形,故本选项正确.故选D.
8.D [解析]
∵直线MN是四边形AMBN的对称轴,∴点A与点B是对应点,
∴AP=BP,AQ=BQ.
∵P是直线MN上的点,
∴∠MAP=∠MBP,
∴A,B,C正确,D错误.
9.解:(1)A',B',C'如图所示.
(2)5
(3)∵△ABC与△A'B'C'关于直线l对称,
∴∠C=∠C'=20°,
∴∠B=180°-∠A-∠C=180°-50°-20°=110°.
10.解:如图所示,△A'B'C'即为所求.
11.C
12.C [解析]
由题意得AD∥BC.因为∠EFB=65°,所以∠DEF=∠EFB=65°.
由轴对称的性质,得∠FED'=∠DEF=65°,所以∠DED'=∠FED'+∠DEF=130°,
所以∠AED'=180°-∠DED'=180°-130°=50°.
13.D [解析]
如图,分别以大正方形的两条对角线AB,EF及MN,CH所在的直线为对称轴,作轴对称图形,则△ABN,△BAM,△EFH,△FEC都是符合题意的三角形.
14.95° [解析]
∵△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,
∴∠C=∠ABO=∠DBO=15°,∠D=∠BAO=∠OAC=25°,∴∠BAC=50°,
∴∠BOC=∠BAC+∠C+∠ABO=80°,∴∠BEC=∠BOC+∠DBO=80°+15°=95°.
15.8 [解析]
由翻折变换的性质可知AD=A'B',A'H=AH,B'G=DG,阴影部分的周长=A'B'+(A'H+BH)+BC+(CG+B'G)=AD+AB+BC+CD=2×4=8.故答案为8.
16.解:(1)①120 [解析]
∵点C和点P关于OA对称,∴∠AOC=∠AOP.∵点P关于OB的对称点是D,∴∠BOD=∠BOP,∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°.故答案为120.
②∵点C和点P关于OA对称,
∴∠AOC=∠AOP.
∵点P关于OB的对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)4 [解析]
根据轴对称的性质,可知CM=PM,DN=PN,∴△PMN的周长为PM+PN+MN=CM+DN+MN=CD=4.
17.解:(1)答案不唯一,如特征1:都是轴对称图形;特征2:图案的总面积都是4.
(2)答案不唯一,如图.
【基础练习】
知识点
1 轴对称图形
1.如图1所示倡导节约的图案中,是轴对称图形的是
( )
图1
2.图2中由“○”和“□”组成轴对称图形,该图形的对称轴是直线
( )
图2
A.l1
B.l2
C.l3
D.l4
3.如图3所示的四个轴对称图形,只有一条对称轴的是
( )
图3
4.画出图4中的各图形的对称轴.
图4
知识点
2 轴对称
5.观察图5中的各组图形,其中成轴对称的为 (只写序号).?
图5
6.如图6,△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是
( )
图6
A.AB
B.DF
C.DE
D.EF
知识点
3 轴对称的性质
7.下列说法中,正确的是
( )
A.
两个全等的三角形一定关于某条直线对称
B.两个图形关于某条直线对称,对应点一定在直线两旁
C.成轴对称的两个图形对应点连线的垂线,就是它们的对称轴
D.关于某条直线对称的两个三角形是全等三角形
8.如图7,直线MN是四边形AMBN的对称轴,与对角线AB交于点Q,P是直线MN上一点,下列判断错误的是
( )
图7
A.AQ=BQ
C.∠MAP=∠MBP
B.AP=BP
D.∠ANM=∠NMB
9.如图8,已知△ABC和△A'B'C'关于直线l成轴对称.
(1)在图中标出点A,B,C的对应点A',B',C';
(2)若AB=5,则对应线段A'B'= ;?
(3)若∠A=50°,∠C'=20°,求∠B的度数.
图8
知识点
4 利用轴对称的性质作图
10.如图9,用三角尺画出△ABC关于直线MN的对称图形.(不写作法,保留作图痕迹)
图9
【能力提升】
11.将一张长方形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可能见到的图形是
( )
图10
12.如图11所示,把一张长方形纸片沿EF折叠后,点D,C分别落在点D',C'的位置.若∠EFB=65°,则∠AED'等于
( )
图11
A.70°
B.65°
C.50°
D.25°
13.如图12,在由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有
( )
图12
A.1个
B.2个
C.3个
D.4个
14.如图13,△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,OC与BD交于点E.若∠C=15°,∠D=25°,则∠BEC的度数为
.?
图13
15.如图14,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为 .?
图14
16.如图15,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB的对称点是D,连接CD交OA于点M,交OB于点N.
(1)①若∠AOB=60°,则∠COD= °;?
②若∠AOB=α,求∠COD的度数.
(2)若CD=4,则△PMN的周长为 .?
图15
17.在如图16所示的网格中,每个小正方形的边长均为1.认真观察图中阴影部分构成的图案,回答下列问题:
图16
(1)请写出四个图案都具有的两个共同特征.
特征1:
;?
特征2:
.?
(2)请在备用图中设计出你心中最美丽的图案,使它也具备你在(1)中写出的特征.
16.1 轴对称
1.C [解析]
根据轴对称图形的定义可以发现A,B,D都不是轴对称图形,只有C符合要求.
2.C
3.A [解析]
A中的图案只有1条对称轴;B中的图案有2条对称轴;C中的图案有4条对称轴;D中的图案有4条对称轴.
4.解:如图.
5.①②④ [解析]
③中的伞把部分不对称,故填①②④.
6.B [解析]
△ABC与△DEF关于直线MN成轴对称,线段AC的对应线段是DF.
7.D [解析]
根据轴对称的性质可知:A项,两个三角形全等,它们不一定关于某条直线对称,故本选项错误.B项,两个图形关于某条直线对称,对应点不一定在直线两旁,还有可能在直线上,故本选项错误.C项,成轴对称的两个图形的对应点连线的垂直平分线,就是它们的对称轴,故本选项错误.D项,两个关于某条直线对称的三角形是全等三角形,故本选项正确.故选D.
8.D [解析]
∵直线MN是四边形AMBN的对称轴,∴点A与点B是对应点,
∴AP=BP,AQ=BQ.
∵P是直线MN上的点,
∴∠MAP=∠MBP,
∴A,B,C正确,D错误.
9.解:(1)A',B',C'如图所示.
(2)5
(3)∵△ABC与△A'B'C'关于直线l对称,
∴∠C=∠C'=20°,
∴∠B=180°-∠A-∠C=180°-50°-20°=110°.
10.解:如图所示,△A'B'C'即为所求.
11.C
12.C [解析]
由题意得AD∥BC.因为∠EFB=65°,所以∠DEF=∠EFB=65°.
由轴对称的性质,得∠FED'=∠DEF=65°,所以∠DED'=∠FED'+∠DEF=130°,
所以∠AED'=180°-∠DED'=180°-130°=50°.
13.D [解析]
如图,分别以大正方形的两条对角线AB,EF及MN,CH所在的直线为对称轴,作轴对称图形,则△ABN,△BAM,△EFH,△FEC都是符合题意的三角形.
14.95° [解析]
∵△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,
∴∠C=∠ABO=∠DBO=15°,∠D=∠BAO=∠OAC=25°,∴∠BAC=50°,
∴∠BOC=∠BAC+∠C+∠ABO=80°,∴∠BEC=∠BOC+∠DBO=80°+15°=95°.
15.8 [解析]
由翻折变换的性质可知AD=A'B',A'H=AH,B'G=DG,阴影部分的周长=A'B'+(A'H+BH)+BC+(CG+B'G)=AD+AB+BC+CD=2×4=8.故答案为8.
16.解:(1)①120 [解析]
∵点C和点P关于OA对称,∴∠AOC=∠AOP.∵点P关于OB的对称点是D,∴∠BOD=∠BOP,∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°.故答案为120.
②∵点C和点P关于OA对称,
∴∠AOC=∠AOP.
∵点P关于OB的对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)4 [解析]
根据轴对称的性质,可知CM=PM,DN=PN,∴△PMN的周长为PM+PN+MN=CM+DN+MN=CD=4.
17.解:(1)答案不唯一,如特征1:都是轴对称图形;特征2:图案的总面积都是4.
(2)答案不唯一,如图.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
