2021—2022学年冀教版八年级数学上册:16.3 角的平分线分层训练(word版,含答案)
文档属性
| 名称 | 2021—2022学年冀教版八年级数学上册:16.3 角的平分线分层训练(word版,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 15:30:10 | ||
图片预览



文档简介
16.3 角的平分线
【基础练习】
知识点
1 角平分线的性质定理
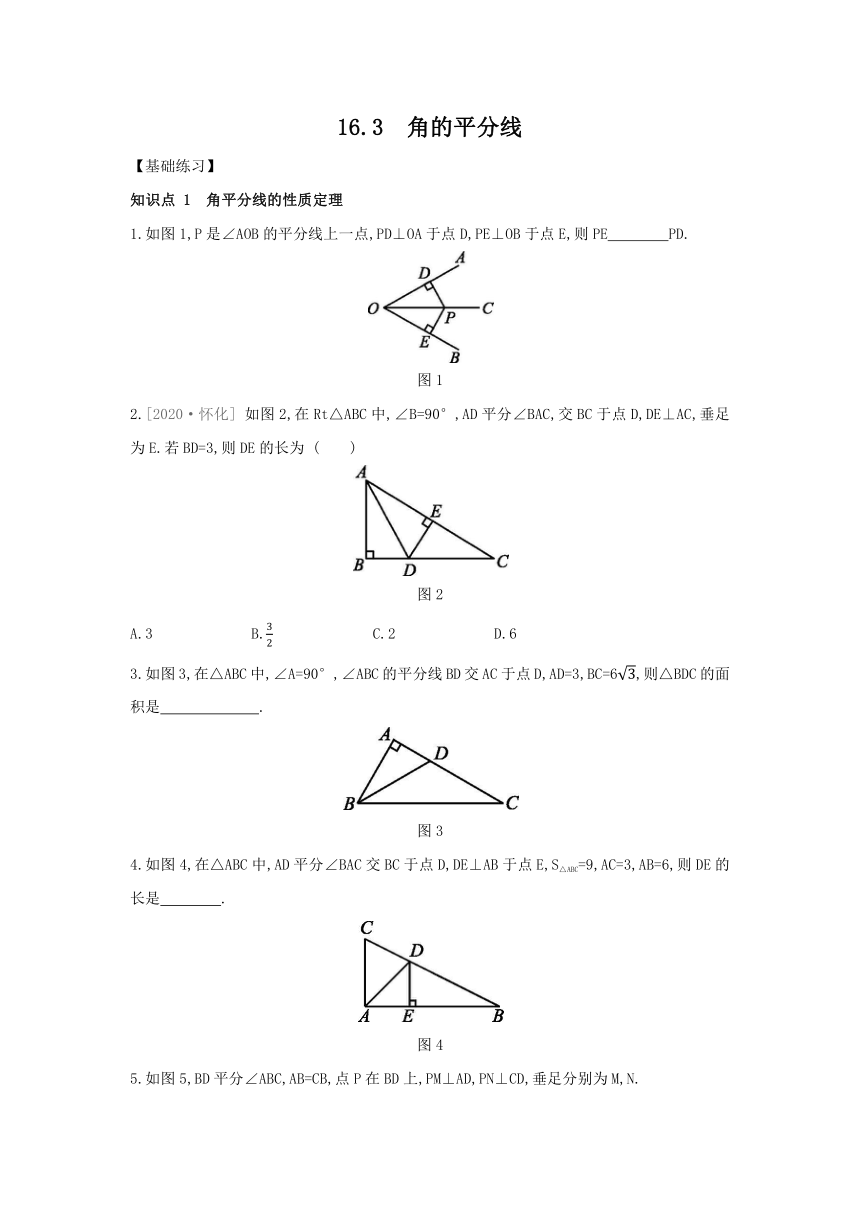
1.如图1,P是∠AOB的平分线上一点,PD⊥OA于点D,PE⊥OB于点E,则PE PD.?
图1
2.[2020·怀化]
如图2,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为E.若BD=3,则DE的长为
( )
图2
A.3
B.
C.2
D.6
3.如图3,在△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=6,则△BDC的面积是
.?
图3
4.如图4,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,S△ABC=9,AC=3,AB=6,则DE的长是 .?
图4
5.如图5,BD平分∠ABC,AB=CB,点P在BD上,PM⊥AD,PN⊥CD,垂足分别为M,N.
求证:PM=PN.
图5
知识点
2 角平分线性质定理的逆定理
6.如图6,∵PM⊥OA,PN⊥OB,PM= ,∴点P在∠AOB的平分线上,即OC平分 .?
图6
7.如图7,直线AB,CD相交于点O,PE⊥AB于点E,PF⊥CD于点F.若PE=PF,且∠AOC=50°,则∠EOP的度数为
( )
图7
A.65°
B.60°
C.45°
D.30°
8.如图8,PB⊥AB,PC⊥AC,垂足分别为B,C,且PB=PC,D是AP上一点.求证:∠BPD=∠CPD.
图8
知识点
3 尺规作图
9.
如图9①,已知∠ABC,用尺规作它的角平分线.
如图②,步骤如下:
第一步:以点B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;
第二步:分别以点D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;
第三步:画射线BP.射线BP即为所求.
下列说法正确的是
( )
图9
A.a,b均无限制
B.a>0,b>DE的长
C.a有最小限制,b无限制
D.a≥0,b10.如图10,在△ABC中,∠C=90°,作△ABC的角平分线AD,交BC于点D(要求:尺规作图,保留作图痕迹,不写作法).
图10
【能力提升】
11.已知在△ABC中,两个完全一样的三角板如图11摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M处,则点M一定在
( )
图11
A.∠A的平分线上
B.AC边的高上
C.BC边的垂直平分线上
D.AB边的中线上
12.[教材复习题C组第5题变式]
如图12,直线a,b,c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有
( )
图12
A.1处
B.2处
C.3处
D.4处
13.如图13,已知AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于点E,且OE=2,则两平行线AB,CD间的距离等于 .?
图13
14.国庆节期间,小红外出游玩时看到了鲜花拼成的“71”字样以及“7”内部的两个花坛M,N,抽象为数学图形具体位置如图14所示,请用尺规作图帮小红找一处观赏位置P,满足观赏点P到AB和BC的距离相等,并且观赏点P到点M,N的距离也相等.(保留作图痕迹,不写作法)
图14
15.已知:如图15,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
(1)求证:AM平分∠DAB;
(2)试猜想线段DM与AM有怎样的位置关系,并证明你的结论.
图15
16.3 角的平分线
1.=
2.A [解析]
∵∠B=90°,∴DB⊥AB.又∵AD平分∠BAC,DE⊥AC,∴DE=BD=3.
3.9 [解析]
过点D作DE⊥BC于点E,根据角平分线的性质求出DE=AD=3,再根据三角形的面积公式求出△BDC的面积即可.
4.2 [解析]
过点D作DH⊥AC于点H.∵AD平分∠BAC,DE⊥AB,DH⊥AC,∴DE=DH.设DE=DH=x.∵S△ADB+S△ADC=S△ABC,∴×3x+×6x=9,解得x=2.
5.证明:在△ABD和△CBD中,∵
∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB.
又∵PM⊥AD,PN⊥CD,∴PM=PN.
6.PN ∠AOB
7.A [解析]
∵PE⊥AB,PF⊥CD,PE=PF,
∴OP平分∠AOD,
∴∠EOP=∠AOD=(180°-∠AOC)=65°.
8.证明:∵PB⊥AB,PC⊥AC,PB=PC,
∴AP平分∠BAC,∴∠BAP=∠CAP.
又∵∠BAP+∠BPD=180°-90°=90°,∠CAP+∠CPD=180°-90°=90°,
∴∠BPD=∠CPD(等角的余角相等).
9.B [解析]
以点B为圆心画弧时,半径a必须大于0,分别以点D,E为圆心,以b为半径画弧时,b必须大于DE的长,否则没有交点.故选B.
10.解:作图如下:
11.A [解析]
如图,作射线AM.由题意,得MG=MH,MG⊥AB,MH⊥AC,∴AM平分∠BAC.
12.D [解析]
∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;
如图,P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,垂足分别为E,D,F,
∴PE=PF,PF=PD,∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足条件的点有3个.
综上,到三条公路的距离相等的点有4个,∴可供选择的地址有4处.
13.4 [解析]
本题考查的是角平分线的性质.过点O作AB的垂线MN分别与AB,CD交于点M,N.
∵AO平分∠BAC,OE⊥AC,MN⊥AB,
∴OM=OE=2.
∵MN⊥AB,AB∥CD,∴MN⊥CD.
∵CO平分∠ACD,OE⊥AC,MN⊥CD,∴ON=OE=2,∴MN=OM+ON=4.故答案为4.
14.解:如图,点P即为所求.
15.解:(1)证明:如图,过点M作ME⊥AD于点E.
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴MC=ME.
∵M是BC的中点,
∴MB=MC,∴MB=ME.
又∵∠B=90°,ME⊥AD,∴AM平分∠DAB.
(2)AM⊥DM.
证明:∵∠B=∠C=90°,∴∠B+∠C=180°,∴AB∥DC,∴∠DAB+∠ADC=180°.
∵AM平分∠DAB,DM平分∠ADC,
∴∠MAD=∠DAB,∠MDA=∠ADC,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,即AM⊥DM.
【基础练习】
知识点
1 角平分线的性质定理
1.如图1,P是∠AOB的平分线上一点,PD⊥OA于点D,PE⊥OB于点E,则PE PD.?
图1
2.[2020·怀化]
如图2,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为E.若BD=3,则DE的长为
( )
图2
A.3
B.
C.2
D.6
3.如图3,在△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=6,则△BDC的面积是
.?
图3
4.如图4,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,S△ABC=9,AC=3,AB=6,则DE的长是 .?
图4
5.如图5,BD平分∠ABC,AB=CB,点P在BD上,PM⊥AD,PN⊥CD,垂足分别为M,N.
求证:PM=PN.
图5
知识点
2 角平分线性质定理的逆定理
6.如图6,∵PM⊥OA,PN⊥OB,PM= ,∴点P在∠AOB的平分线上,即OC平分 .?
图6
7.如图7,直线AB,CD相交于点O,PE⊥AB于点E,PF⊥CD于点F.若PE=PF,且∠AOC=50°,则∠EOP的度数为
( )
图7
A.65°
B.60°
C.45°
D.30°
8.如图8,PB⊥AB,PC⊥AC,垂足分别为B,C,且PB=PC,D是AP上一点.求证:∠BPD=∠CPD.
图8
知识点
3 尺规作图
9.
如图9①,已知∠ABC,用尺规作它的角平分线.
如图②,步骤如下:
第一步:以点B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;
第二步:分别以点D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;
第三步:画射线BP.射线BP即为所求.
下列说法正确的是
( )
图9
A.a,b均无限制
B.a>0,b>DE的长
C.a有最小限制,b无限制
D.a≥0,b
图10
【能力提升】
11.已知在△ABC中,两个完全一样的三角板如图11摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M处,则点M一定在
( )
图11
A.∠A的平分线上
B.AC边的高上
C.BC边的垂直平分线上
D.AB边的中线上
12.[教材复习题C组第5题变式]
如图12,直线a,b,c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有
( )
图12
A.1处
B.2处
C.3处
D.4处
13.如图13,已知AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于点E,且OE=2,则两平行线AB,CD间的距离等于 .?
图13
14.国庆节期间,小红外出游玩时看到了鲜花拼成的“71”字样以及“7”内部的两个花坛M,N,抽象为数学图形具体位置如图14所示,请用尺规作图帮小红找一处观赏位置P,满足观赏点P到AB和BC的距离相等,并且观赏点P到点M,N的距离也相等.(保留作图痕迹,不写作法)
图14
15.已知:如图15,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
(1)求证:AM平分∠DAB;
(2)试猜想线段DM与AM有怎样的位置关系,并证明你的结论.
图15
16.3 角的平分线
1.=
2.A [解析]
∵∠B=90°,∴DB⊥AB.又∵AD平分∠BAC,DE⊥AC,∴DE=BD=3.
3.9 [解析]
过点D作DE⊥BC于点E,根据角平分线的性质求出DE=AD=3,再根据三角形的面积公式求出△BDC的面积即可.
4.2 [解析]
过点D作DH⊥AC于点H.∵AD平分∠BAC,DE⊥AB,DH⊥AC,∴DE=DH.设DE=DH=x.∵S△ADB+S△ADC=S△ABC,∴×3x+×6x=9,解得x=2.
5.证明:在△ABD和△CBD中,∵
∴△ABD≌△CBD(SAS),∴∠ADB=∠CDB.
又∵PM⊥AD,PN⊥CD,∴PM=PN.
6.PN ∠AOB
7.A [解析]
∵PE⊥AB,PF⊥CD,PE=PF,
∴OP平分∠AOD,
∴∠EOP=∠AOD=(180°-∠AOC)=65°.
8.证明:∵PB⊥AB,PC⊥AC,PB=PC,
∴AP平分∠BAC,∴∠BAP=∠CAP.
又∵∠BAP+∠BPD=180°-90°=90°,∠CAP+∠CPD=180°-90°=90°,
∴∠BPD=∠CPD(等角的余角相等).
9.B [解析]
以点B为圆心画弧时,半径a必须大于0,分别以点D,E为圆心,以b为半径画弧时,b必须大于DE的长,否则没有交点.故选B.
10.解:作图如下:
11.A [解析]
如图,作射线AM.由题意,得MG=MH,MG⊥AB,MH⊥AC,∴AM平分∠BAC.
12.D [解析]
∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;
如图,P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,垂足分别为E,D,F,
∴PE=PF,PF=PD,∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足条件的点有3个.
综上,到三条公路的距离相等的点有4个,∴可供选择的地址有4处.
13.4 [解析]
本题考查的是角平分线的性质.过点O作AB的垂线MN分别与AB,CD交于点M,N.
∵AO平分∠BAC,OE⊥AC,MN⊥AB,
∴OM=OE=2.
∵MN⊥AB,AB∥CD,∴MN⊥CD.
∵CO平分∠ACD,OE⊥AC,MN⊥CD,∴ON=OE=2,∴MN=OM+ON=4.故答案为4.
14.解:如图,点P即为所求.
15.解:(1)证明:如图,过点M作ME⊥AD于点E.
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴MC=ME.
∵M是BC的中点,
∴MB=MC,∴MB=ME.
又∵∠B=90°,ME⊥AD,∴AM平分∠DAB.
(2)AM⊥DM.
证明:∵∠B=∠C=90°,∴∠B+∠C=180°,∴AB∥DC,∴∠DAB+∠ADC=180°.
∵AM平分∠DAB,DM平分∠ADC,
∴∠MAD=∠DAB,∠MDA=∠ADC,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,即AM⊥DM.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
