2021—2022学年冀教版八年级数学上册16.1—16.3练习题(word解析版)
文档属性
| 名称 | 2021—2022学年冀教版八年级数学上册16.1—16.3练习题(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 278.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览


文档简介
16.1——16.3
一、选择题(每小题5分,共35分)
1.下列四个图形中,是轴对称图形的是
( )
图1
2.下列图形中,只有一条对称轴的轴对称图形是
( )
图2
3.尺规作图要求:(Ⅰ)过直线外一点作这条直线的垂线;(Ⅱ)作线段的垂直平分线;(Ⅲ)过直线上一点作这条直线的垂线;(Ⅳ)作角的平分线.
图3是按上述要求排乱顺序的尺规作图:
图3
则正确的配对是
( )
A.①-Ⅳ,②-Ⅱ,③-Ⅰ,④-Ⅲ
B.①-Ⅳ,②-Ⅲ,③-Ⅱ,④-Ⅰ
C.①-Ⅱ,②-Ⅳ,③-Ⅲ,④-Ⅰ
D.①-Ⅳ,②-Ⅰ,③-Ⅱ,④-Ⅲ
4.如图4,DE垂直平分AC,△ABD的周长是8.5
cm,AC=3
cm,则△ABC的周长是
( )
图4
A.8.5
cm
B.10
cm
C.11.5
cm
D.13
cm
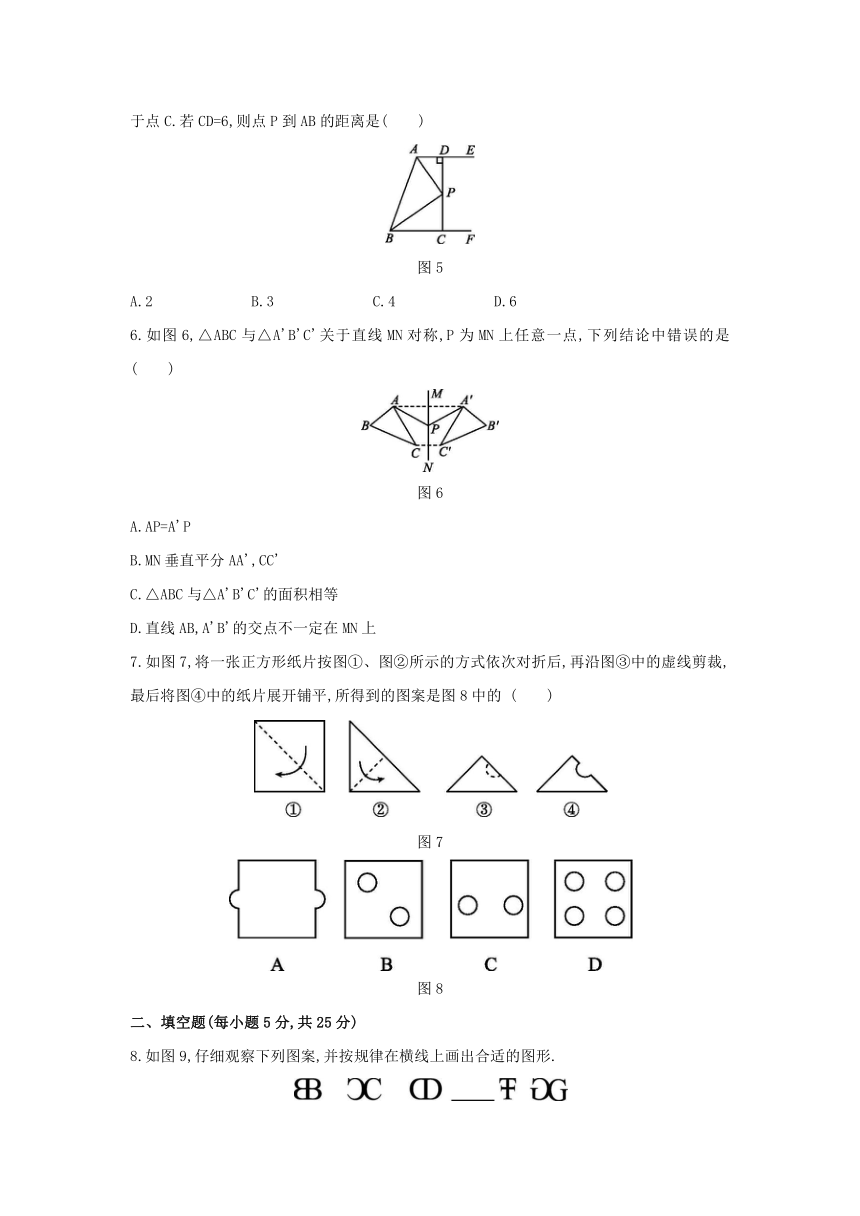
5.如图5,AE∥BF,∠BAE和∠ABF的平分线交于点P,过点P作PD⊥AE于点D,延长DP交BF于点C.若CD=6,则点P到AB的距离是( )
图5
A.2
B.3
C.4
D.6
6.如图6,△ABC与△A'B'C'关于直线MN对称,P为MN上任意一点,下列结论中错误的是
( )
图6
A.AP=A'P
B.MN垂直平分AA',CC'
C.△ABC与△A'B'C'的面积相等
D.直线AB,A'B'的交点不一定在MN上
7.如图7,将一张正方形纸片按图①、图②所示的方式依次对折后,再沿图③中的虚线剪裁,最后将图④中的纸片展开铺平,所得到的图案是图8中的
( )
图7
图8
二、填空题(每小题5分,共25分)
8.如图9,仔细观察下列图案,并按规律在横线上画出合适的图形.
图9
9.如图10,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是 .?
图10
10.如图11,OP平分∠MON,PA⊥ON于点A,Q是射线OM上的一个动点.若PA=2,则PQ长的最小值为 .?
图11
11.如图12,在△ABC中,∠B=55°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为 .?
图12
12.如图13,在△ABC中,∠A=36°,∠C=72°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.有下列结论:
①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BDO;④点D到线段BC的距离等于线段OD的长.
其中正确的是 .(把所有正确结论的序号都填在横线上)?
图13
三、解答题(共40分)
13.(12分)如图14,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1(要求:点A与点A1,点B与点B1,点C与点C1相对应);
(2)在第(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
图14
14.(14分)如图15,在△ABC中,∠ABC的平分线与△ABC的外角∠ACE的平分线交于点P,PD⊥AC于点D,PH⊥BA,交BA的延长线于点H.
(1)若PH=8
cm,求点P到直线BC的距离;
(2)求证:点P在∠HAC的平分线上.
图15
15.(14分)如图16,在△ABC中,∠C=90°,DE是AB的垂直平分线,垂足为E,交BC于点D,连接AD.
(1)若AC=5,BC=7,求△ACD的周长;
(2)若∠BAD∶∠CAD=2∶1,求∠B的度数.
图16
答案
1.D
2.D [解析]
A.不是轴对称图形,没有对称轴;B.有四条对称轴;C.有四条对称轴;D.只有一条对称轴.
3.D
4.C [解析]
∵DE垂直平分AC,
∴AD=CD,故可得出AB+BD+AD=AB+BC=8.5
cm.
∵AC=3
cm,∴△ABC的周长=AB+BC+AC=8.5+3=11.5(cm).
5.B [解析]
如图,过点P作PH⊥AB于点H.
∵AP平分∠BAE,PH⊥AB,PD⊥AE,
∴PH=PD,
同理可得PH=PC,∴PH=PC=PD.
又∵PC+PD=CD=6,∴PH=PC=3,
∴点P到AB的距离是3.
6.D [解析]
本题考查轴对称的性质与运用,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
∵△ABC与△A'B'C'关于直线MN对称,P为MN上任意一点,
∴MN垂直平分AA',CC',AP=A'P,△ABC与△A'B'C'的面积相等,故A,B,C选项正确;
∵AB,A'B'关于直线MN对称,∴其交点一定在MN上.故D选项错误.
7.B [解析]
严格按照图中的顺序进行操作,展开得到的图形如选项B所示.故选B.
8.
9.16 [解析]
∵DE是AB的垂直平分线,∴AE=BE.∵AC=10,BC=6,∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=6+10=16.
10.2
11.69° [解析]
∵在△ABC中,∠B=55°,∠C=28°,∴∠BAC=180°-55°-28°=97°.
由直线MN是线段AC的垂直平分线,
易得∠CAD=∠C=28°,
∴∠BAD=∠BAC-∠CAD=97°-28°=69°.
12.①②④
13.解:(1)如图,△A1B1C1是△ABC关于直线l对称的图形.
(2)由图得四边形BB1C1C是梯形,BB1=4,CC1=2,高是4,
∴=(BB1+CC1)×4=×(4+2)×4=12.
14.解:(1)过点P作PQ⊥BE于点Q,如图.
∵BP平分∠ABC,PH⊥BA,PQ⊥BC,
∴PQ=PH=8
cm,
即点P到直线BC的距离为8
cm.
(2)证明:∵CP平分∠ACE,PD⊥AC,PQ⊥BE,∴PD=PQ.
由(1)知,PH=PQ,∴PD=PH.
又∵PD⊥AC,PH⊥BA,
∴点P在∠HAC的平分线上.
15.解:(1)∵DE是AB的垂直平分线,∴DA=DB,
∴△ACD的周长=AC+CD+DA=AC+CD+DB=AC+BC=5+7=12.
(2)在△EAD与△EBD中,∵
∴△EAD≌△EBD,∴∠BAD=∠B.
设∠CAD=x,则∠BAD=∠B=2x.
∵∠C=90°,
∴∠CAB+∠B=90°,即x+2x+2x=90°,
解得x=18°,∴∠B=2x=36°.
一、选择题(每小题5分,共35分)
1.下列四个图形中,是轴对称图形的是
( )
图1
2.下列图形中,只有一条对称轴的轴对称图形是
( )
图2
3.尺规作图要求:(Ⅰ)过直线外一点作这条直线的垂线;(Ⅱ)作线段的垂直平分线;(Ⅲ)过直线上一点作这条直线的垂线;(Ⅳ)作角的平分线.
图3是按上述要求排乱顺序的尺规作图:
图3
则正确的配对是
( )
A.①-Ⅳ,②-Ⅱ,③-Ⅰ,④-Ⅲ
B.①-Ⅳ,②-Ⅲ,③-Ⅱ,④-Ⅰ
C.①-Ⅱ,②-Ⅳ,③-Ⅲ,④-Ⅰ
D.①-Ⅳ,②-Ⅰ,③-Ⅱ,④-Ⅲ
4.如图4,DE垂直平分AC,△ABD的周长是8.5
cm,AC=3
cm,则△ABC的周长是
( )
图4
A.8.5
cm
B.10
cm
C.11.5
cm
D.13
cm
5.如图5,AE∥BF,∠BAE和∠ABF的平分线交于点P,过点P作PD⊥AE于点D,延长DP交BF于点C.若CD=6,则点P到AB的距离是( )
图5
A.2
B.3
C.4
D.6
6.如图6,△ABC与△A'B'C'关于直线MN对称,P为MN上任意一点,下列结论中错误的是
( )
图6
A.AP=A'P
B.MN垂直平分AA',CC'
C.△ABC与△A'B'C'的面积相等
D.直线AB,A'B'的交点不一定在MN上
7.如图7,将一张正方形纸片按图①、图②所示的方式依次对折后,再沿图③中的虚线剪裁,最后将图④中的纸片展开铺平,所得到的图案是图8中的
( )
图7
图8
二、填空题(每小题5分,共25分)
8.如图9,仔细观察下列图案,并按规律在横线上画出合适的图形.
图9
9.如图10,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是 .?
图10
10.如图11,OP平分∠MON,PA⊥ON于点A,Q是射线OM上的一个动点.若PA=2,则PQ长的最小值为 .?
图11
11.如图12,在△ABC中,∠B=55°,∠C=28°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为 .?
图12
12.如图13,在△ABC中,∠A=36°,∠C=72°,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.有下列结论:
①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BDO;④点D到线段BC的距离等于线段OD的长.
其中正确的是 .(把所有正确结论的序号都填在横线上)?
图13
三、解答题(共40分)
13.(12分)如图14,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1(要求:点A与点A1,点B与点B1,点C与点C1相对应);
(2)在第(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
图14
14.(14分)如图15,在△ABC中,∠ABC的平分线与△ABC的外角∠ACE的平分线交于点P,PD⊥AC于点D,PH⊥BA,交BA的延长线于点H.
(1)若PH=8
cm,求点P到直线BC的距离;
(2)求证:点P在∠HAC的平分线上.
图15
15.(14分)如图16,在△ABC中,∠C=90°,DE是AB的垂直平分线,垂足为E,交BC于点D,连接AD.
(1)若AC=5,BC=7,求△ACD的周长;
(2)若∠BAD∶∠CAD=2∶1,求∠B的度数.
图16
答案
1.D
2.D [解析]
A.不是轴对称图形,没有对称轴;B.有四条对称轴;C.有四条对称轴;D.只有一条对称轴.
3.D
4.C [解析]
∵DE垂直平分AC,
∴AD=CD,故可得出AB+BD+AD=AB+BC=8.5
cm.
∵AC=3
cm,∴△ABC的周长=AB+BC+AC=8.5+3=11.5(cm).
5.B [解析]
如图,过点P作PH⊥AB于点H.
∵AP平分∠BAE,PH⊥AB,PD⊥AE,
∴PH=PD,
同理可得PH=PC,∴PH=PC=PD.
又∵PC+PD=CD=6,∴PH=PC=3,
∴点P到AB的距离是3.
6.D [解析]
本题考查轴对称的性质与运用,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
∵△ABC与△A'B'C'关于直线MN对称,P为MN上任意一点,
∴MN垂直平分AA',CC',AP=A'P,△ABC与△A'B'C'的面积相等,故A,B,C选项正确;
∵AB,A'B'关于直线MN对称,∴其交点一定在MN上.故D选项错误.
7.B [解析]
严格按照图中的顺序进行操作,展开得到的图形如选项B所示.故选B.
8.
9.16 [解析]
∵DE是AB的垂直平分线,∴AE=BE.∵AC=10,BC=6,∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=6+10=16.
10.2
11.69° [解析]
∵在△ABC中,∠B=55°,∠C=28°,∴∠BAC=180°-55°-28°=97°.
由直线MN是线段AC的垂直平分线,
易得∠CAD=∠C=28°,
∴∠BAD=∠BAC-∠CAD=97°-28°=69°.
12.①②④
13.解:(1)如图,△A1B1C1是△ABC关于直线l对称的图形.
(2)由图得四边形BB1C1C是梯形,BB1=4,CC1=2,高是4,
∴=(BB1+CC1)×4=×(4+2)×4=12.
14.解:(1)过点P作PQ⊥BE于点Q,如图.
∵BP平分∠ABC,PH⊥BA,PQ⊥BC,
∴PQ=PH=8
cm,
即点P到直线BC的距离为8
cm.
(2)证明:∵CP平分∠ACE,PD⊥AC,PQ⊥BE,∴PD=PQ.
由(1)知,PH=PQ,∴PD=PH.
又∵PD⊥AC,PH⊥BA,
∴点P在∠HAC的平分线上.
15.解:(1)∵DE是AB的垂直平分线,∴DA=DB,
∴△ACD的周长=AC+CD+DA=AC+CD+DB=AC+BC=5+7=12.
(2)在△EAD与△EBD中,∵
∴△EAD≌△EBD,∴∠BAD=∠B.
设∠CAD=x,则∠BAD=∠B=2x.
∵∠C=90°,
∴∠CAB+∠B=90°,即x+2x+2x=90°,
解得x=18°,∴∠B=2x=36°.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
