2021-2022学年冀教版九年级数学上册 23.3.2 方差的应用 课时训练卷(word含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册 23.3.2 方差的应用 课时训练卷(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览



文档简介
冀教版九年级数学上册
23.3.2
方差的应用
课时训练卷
一、选择题(共8小题,4
8=32)
1.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们的成绩的(
)
A.众数
B.中位数
C.方差
D.以上都不对
2.甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是s甲2=1.2,s乙2=1.1,s丙2=0.6,s丁2=0.9,则射击成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁
3.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数/cm
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中的数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择(
)
A.甲
B.乙
C.丙
D.丁
4.去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差s2(单位:千克2)如表所示:
甲
乙
丙
丁
x
24
24
23
20
s2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是(
)
A.甲
B.乙
C.丙
D.丁
5.在一次比赛中,有5位裁判分别给某位选手的打分情况如下表,
裁判人数
2
2
1
选手得分
9.1
9.3
9.7
则这位选手得分的平均数和方差分别是( )
A.
9.3,0.04
B.9.3,0.048
C.9.22,0.048
D.9.37,0.04
6.
已知A样本的数据如下:72,73,76,76,77,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数
B.方差
C.中位数
D.众数
7.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是x甲=610千克,x乙=608千克,亩产量的方差分别为s甲2=29.6,s乙2=2.7,则关于两种小麦推广种植的合理决策是(
)
A.甲的平均亩产量较高,应推广甲
B.甲、乙的平均亩产量相差不多,均可推广
C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
8.甲、乙两人连续5次射击成绩如图所示,下列说法中正确的是( )
A.甲的成绩更稳定
B.乙的成绩更稳定
C.甲、乙的成绩一样稳定
D.无法判断谁的成绩更稳定
二.填空题(共6小题,4
6=24)
9.甲、乙、丙、丁参加体育训练,近期10次跳绳测试的平均成绩都是每分钟174个,其方差如下表:
选手
甲
乙
丙
丁
方差
0.023
0.018
0.020
0.021
则这10次跳绳中,这四个人发挥最稳定的是________.
10.
从甲、乙、丙、丁四人中选一人参加射击比赛,经过三轮初赛,他们的平均成绩都是9环,方差分别是s甲2=0.25,s乙2=0.3,s丙2=0.4,s丁2=0.35,你认为派________去参赛更合适.
11.为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛,我市四名中学生参加了男子100
m自由泳训练,他们成绩的平均数及其方差s2如下表所示:
甲
乙
丙
丁
1′05″33
1′04″26
1′04″26
1′07″29
s2
1.1
1.1
1.3
1.6
如果选拔一名学生去参赛,应派______去.
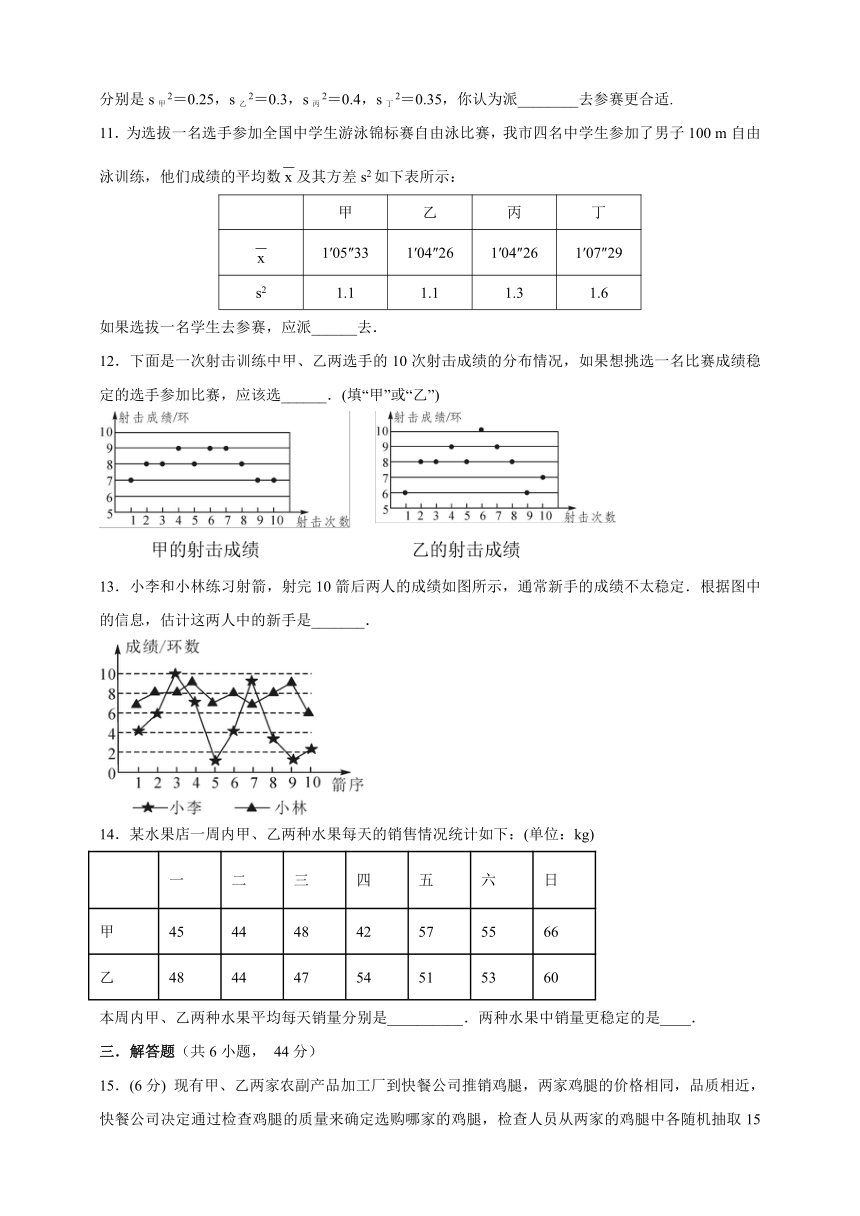
12.下面是一次射击训练中甲、乙两选手的10次射击成绩的分布情况,如果想挑选一名比赛成绩稳定的选手参加比赛,应该选______.(填“甲”或“乙”)
13.小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定.根据图中的信息,估计这两人中的新手是_______.
14.某水果店一周内甲、乙两种水果每天的销售情况统计如下:(单位:kg)
一
二
三
四
五
六
日
甲
45
44
48
42
57
55
66
乙
48
44
47
54
51
53
60
本周内甲、乙两种水果平均每天销量分别是__________.两种水果中销量更稳定的是____.
三.解答题(共6小题,
44分)
15.(6分)
现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近,快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿,检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.
质量(g)
73
74
75
76
77
78
甲的数量
2
4
4
3
1
1
乙的数量
2
3
6
2
1
1
根据表中数据,回答下列问题:
(1)甲厂抽取质量的中位数是_____g,乙厂抽取质量的众数是_____g;
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数x乙=75,方差s乙2≈1.73.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿
16.(8分)
甲、乙两名工人同时加工10个同一种零件,加工后对零件的长度进行检测,结果如下:(单位:mm)
甲:19.9,19.7,19.8,20.0,20.2,20.1,19.9,20.3,20.1,20.2;
乙:20.2,20.4,20.0,19.9,20.2,19.8,19.7,20.1,19.7,20.2.
(1)分别计算上面两组数据的平均数和方差;
(2)若技术要求零件长度为20.0±0.5(mm),根据上面的计算,说明哪个工人加工的10个零件质量比较稳定.
17.(8分)
王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已结果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明哪个山上的杨梅产量较稳定.
18.(10分)
八年级一、二班举行投篮比赛,每班各挑选10名同学代表班级参加7轮积分赛,投篮命中率如下:
场次
1
2
3
4
5
6
7
一班
85%
88%
77%
75%
85%
80%
70%
二班
90%
85%
70%
80%
60%
83%
92%
你认为哪个班级的投篮命中率较稳定?为什么?
19.(12分)
某厂生产A,B两种产品,其单价随市场变化而进行相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图(如图).
A,B产品单价变化统计表
第一次
第二次
第三次
A产品单价/(元/件)
6
5.2
6.5
B产品单价/(元/件)
3.5
4
3
并求得了A产品三次单价数据的平均数和方差:
xA=5.9;sA2=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了________%;
(2)求B产品三次单价数据的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数比B产品这四次单价中位数的2倍少1,求m的值.
参考答案
1-4CCAB
5-8BBDB
9.
乙
10.
甲
11.
乙
12.
甲
13.
小李
14.
51,51,乙
15.
解:(1)75,75
(2)x甲=75,s甲2≈1.87,∵x甲=x乙,s甲2>s乙2,∴两家加工厂的鸡腿质量大致相等,但乙加工厂的鸡腿质量更稳定,因此快餐公司应选购乙加工厂生产的鸡腿
16.
解:(1)甲的平均数和方差分别为20.02,0.0336,乙的平均数和方差分别为20.02,0.0516
(2)甲加工的质量比较稳定
17.
解:(1)x甲=40,x乙=40,总产量为40×100×98%×2=7840(千克)
(2)s甲2=[(50-40)2+(36-40)2+(40-40)2+(34-40)2]=38,s乙2=[(36-40)2+(40-40)2+(48-40)2+(36-40)2]=24,s甲2>s乙2,∴乙山上的杨梅产量较稳定
18.
解:一班投篮命中率的平均数是:x-=(85%+88%+77%+75%+85%+80%+70%)÷7=80%;一班投篮命中率的方差是:s2=[(85%-80%)2+(88%-80%)2+(77%-80%)2+(75%-80%)2+(85%-80%)2+(80%-80%)2+(70%-80%)2]÷7=0.0035429;
二班投篮命中率的平均数是:x-=(90%+85%+70%+80%+60%+83%+92%)÷7=80%;二班投篮命中率的方差是:s2=[(90%-80%)2+(85%-80%)2+(70%-80%)2+(80%-80%)2+(60%-80%)2+(83%-80%)2+(92%-80%)2]÷7=0.0111143.
∴一班的方差s2<二班的方差s2.
∴一班的投篮命中率较稳定.
19.
解:(1)如图所示.
25.
(2)B产品三次单价数据的平均数为xB=×(3.5+4+3)=3.5,方差为sB2==.
因为<,所以B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=(元/件).对于B产品,因为m>0,所以第四次单价大于3元/件.又因为×2-1=>,所以第四次单价小于4元/件.所以×2-1=.
所以m=25.
23.3.2
方差的应用
课时训练卷
一、选择题(共8小题,4
8=32)
1.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们的成绩的(
)
A.众数
B.中位数
C.方差
D.以上都不对
2.甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是s甲2=1.2,s乙2=1.1,s丙2=0.6,s丁2=0.9,则射击成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁
3.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数/cm
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中的数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择(
)
A.甲
B.乙
C.丙
D.丁
4.去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差s2(单位:千克2)如表所示:
甲
乙
丙
丁
x
24
24
23
20
s2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是(
)
A.甲
B.乙
C.丙
D.丁
5.在一次比赛中,有5位裁判分别给某位选手的打分情况如下表,
裁判人数
2
2
1
选手得分
9.1
9.3
9.7
则这位选手得分的平均数和方差分别是( )
A.
9.3,0.04
B.9.3,0.048
C.9.22,0.048
D.9.37,0.04
6.
已知A样本的数据如下:72,73,76,76,77,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数
B.方差
C.中位数
D.众数
7.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是x甲=610千克,x乙=608千克,亩产量的方差分别为s甲2=29.6,s乙2=2.7,则关于两种小麦推广种植的合理决策是(
)
A.甲的平均亩产量较高,应推广甲
B.甲、乙的平均亩产量相差不多,均可推广
C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
8.甲、乙两人连续5次射击成绩如图所示,下列说法中正确的是( )
A.甲的成绩更稳定
B.乙的成绩更稳定
C.甲、乙的成绩一样稳定
D.无法判断谁的成绩更稳定
二.填空题(共6小题,4
6=24)
9.甲、乙、丙、丁参加体育训练,近期10次跳绳测试的平均成绩都是每分钟174个,其方差如下表:
选手
甲
乙
丙
丁
方差
0.023
0.018
0.020
0.021
则这10次跳绳中,这四个人发挥最稳定的是________.
10.
从甲、乙、丙、丁四人中选一人参加射击比赛,经过三轮初赛,他们的平均成绩都是9环,方差分别是s甲2=0.25,s乙2=0.3,s丙2=0.4,s丁2=0.35,你认为派________去参赛更合适.
11.为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛,我市四名中学生参加了男子100
m自由泳训练,他们成绩的平均数及其方差s2如下表所示:
甲
乙
丙
丁
1′05″33
1′04″26
1′04″26
1′07″29
s2
1.1
1.1
1.3
1.6
如果选拔一名学生去参赛,应派______去.
12.下面是一次射击训练中甲、乙两选手的10次射击成绩的分布情况,如果想挑选一名比赛成绩稳定的选手参加比赛,应该选______.(填“甲”或“乙”)
13.小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定.根据图中的信息,估计这两人中的新手是_______.
14.某水果店一周内甲、乙两种水果每天的销售情况统计如下:(单位:kg)
一
二
三
四
五
六
日
甲
45
44
48
42
57
55
66
乙
48
44
47
54
51
53
60
本周内甲、乙两种水果平均每天销量分别是__________.两种水果中销量更稳定的是____.
三.解答题(共6小题,
44分)
15.(6分)
现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近,快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿,检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.
质量(g)
73
74
75
76
77
78
甲的数量
2
4
4
3
1
1
乙的数量
2
3
6
2
1
1
根据表中数据,回答下列问题:
(1)甲厂抽取质量的中位数是_____g,乙厂抽取质量的众数是_____g;
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数x乙=75,方差s乙2≈1.73.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿
16.(8分)
甲、乙两名工人同时加工10个同一种零件,加工后对零件的长度进行检测,结果如下:(单位:mm)
甲:19.9,19.7,19.8,20.0,20.2,20.1,19.9,20.3,20.1,20.2;
乙:20.2,20.4,20.0,19.9,20.2,19.8,19.7,20.1,19.7,20.2.
(1)分别计算上面两组数据的平均数和方差;
(2)若技术要求零件长度为20.0±0.5(mm),根据上面的计算,说明哪个工人加工的10个零件质量比较稳定.
17.(8分)
王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已结果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明哪个山上的杨梅产量较稳定.
18.(10分)
八年级一、二班举行投篮比赛,每班各挑选10名同学代表班级参加7轮积分赛,投篮命中率如下:
场次
1
2
3
4
5
6
7
一班
85%
88%
77%
75%
85%
80%
70%
二班
90%
85%
70%
80%
60%
83%
92%
你认为哪个班级的投篮命中率较稳定?为什么?
19.(12分)
某厂生产A,B两种产品,其单价随市场变化而进行相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图(如图).
A,B产品单价变化统计表
第一次
第二次
第三次
A产品单价/(元/件)
6
5.2
6.5
B产品单价/(元/件)
3.5
4
3
并求得了A产品三次单价数据的平均数和方差:
xA=5.9;sA2=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了________%;
(2)求B产品三次单价数据的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数比B产品这四次单价中位数的2倍少1,求m的值.
参考答案
1-4CCAB
5-8BBDB
9.
乙
10.
甲
11.
乙
12.
甲
13.
小李
14.
51,51,乙
15.
解:(1)75,75
(2)x甲=75,s甲2≈1.87,∵x甲=x乙,s甲2>s乙2,∴两家加工厂的鸡腿质量大致相等,但乙加工厂的鸡腿质量更稳定,因此快餐公司应选购乙加工厂生产的鸡腿
16.
解:(1)甲的平均数和方差分别为20.02,0.0336,乙的平均数和方差分别为20.02,0.0516
(2)甲加工的质量比较稳定
17.
解:(1)x甲=40,x乙=40,总产量为40×100×98%×2=7840(千克)
(2)s甲2=[(50-40)2+(36-40)2+(40-40)2+(34-40)2]=38,s乙2=[(36-40)2+(40-40)2+(48-40)2+(36-40)2]=24,s甲2>s乙2,∴乙山上的杨梅产量较稳定
18.
解:一班投篮命中率的平均数是:x-=(85%+88%+77%+75%+85%+80%+70%)÷7=80%;一班投篮命中率的方差是:s2=[(85%-80%)2+(88%-80%)2+(77%-80%)2+(75%-80%)2+(85%-80%)2+(80%-80%)2+(70%-80%)2]÷7=0.0035429;
二班投篮命中率的平均数是:x-=(90%+85%+70%+80%+60%+83%+92%)÷7=80%;二班投篮命中率的方差是:s2=[(90%-80%)2+(85%-80%)2+(70%-80%)2+(80%-80%)2+(60%-80%)2+(83%-80%)2+(92%-80%)2]÷7=0.0111143.
∴一班的方差s2<二班的方差s2.
∴一班的投篮命中率较稳定.
19.
解:(1)如图所示.
25.
(2)B产品三次单价数据的平均数为xB=×(3.5+4+3)=3.5,方差为sB2==.
因为<,所以B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=(元/件).对于B产品,因为m>0,所以第四次单价大于3元/件.又因为×2-1=>,所以第四次单价小于4元/件.所以×2-1=.
所以m=25.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
