2021—2022学年冀教版九年级数学上册25.3相似三角形 同步练习题(word版含答案)
文档属性
| 名称 | 2021—2022学年冀教版九年级数学上册25.3相似三角形 同步练习题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 131.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 19:12:50 | ||
图片预览


文档简介
25.3 相似三角形
【基础练习】
知识点
1 相似三角形的相关定义
1.如图1所示,D是△ABC的边AB上的一点,当∠ADC=∠ACB,∠ACD= ,∠A=∠A,==时,△ADC △ACB.?
图1
2.
下列说法中,错误的是
( )
A.两个全等三角形一定是相似三角形
B.两个等腰三角形一定相似
C.两个等边三角形一定相似
D.两个等腰直角三角形一定相似
3.若△ABC∽△DEF,AB=4cm,DE=8cm,则△ABC与△DEF的相似比为 ,△DEF与△ABC的相似比为 .?
知识点
2 相似三角形的应用
4.如图2,△ADE∽△ACB,则
图2
(1)==;
(2)∠ADE= ,∠AED= .?
5.已知△ABC∽△DEF,AB=6cm,BC=4cm,AC=9cm,且△DEF的最短边的长为8cm,则最长边的长为
( )
A.16cm
B.18cm
C.4.5cm
D.13cm
6.如图3,已知△ABC∽△DEB,BE=3,CE=2,则的值为
( )
图3
A.
B.
C.
D.
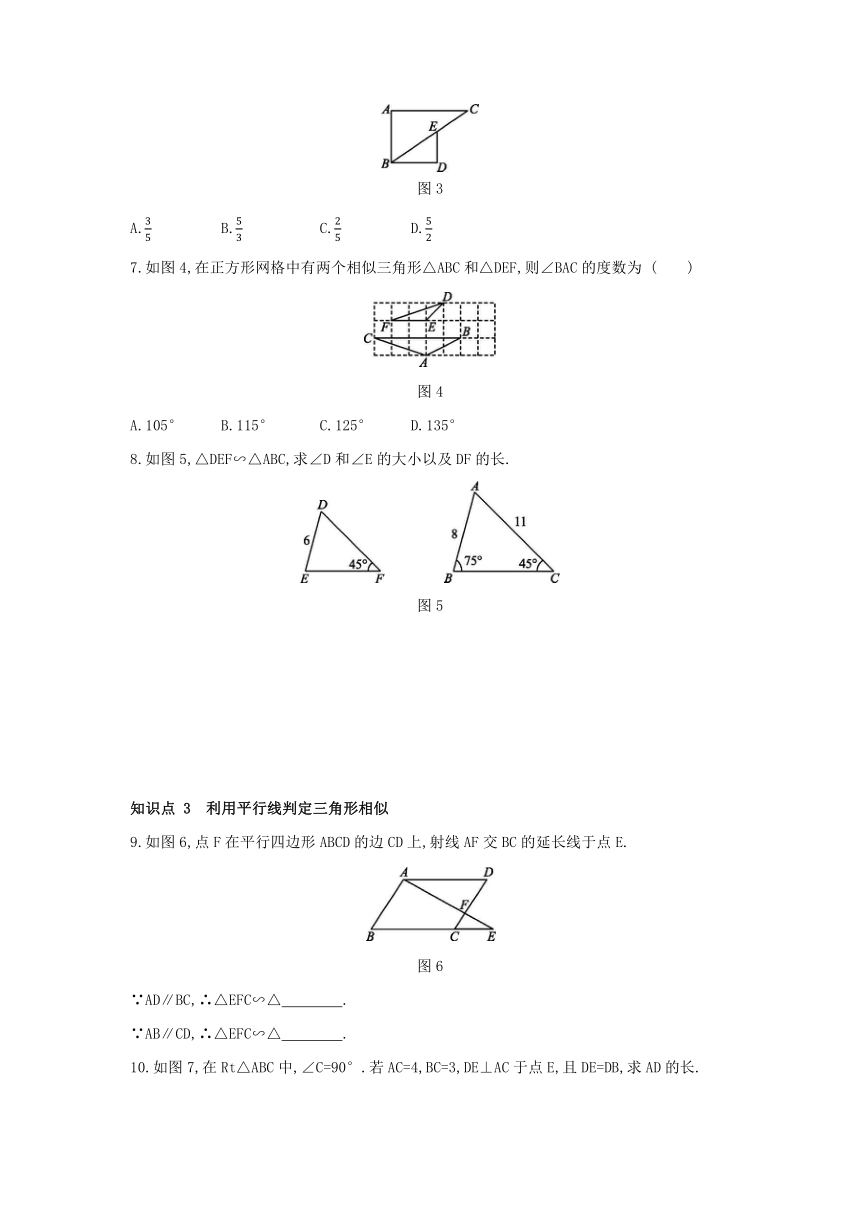
7.如图4,在正方形网格中有两个相似三角形△ABC和△DEF,则∠BAC的度数为
( )
图4
A.105°
B.115°
C.125°
D.135°
8.如图5,△DEF∽△ABC,求∠D和∠E的大小以及DF的长.
图5
知识点
3 利用平行线判定三角形相似
9.如图6,点F在平行四边形ABCD的边CD上,射线AF交BC的延长线于点E.
图6
∵AD∥BC,∴△EFC∽△ .?
∵AB∥CD,∴△EFC∽△ .?
10.如图7,在Rt△ABC中,∠C=90°.若AC=4,BC=3,DE⊥AC于点E,且DE=DB,求AD的长.
图7
【能力提升】
11.如图8,在△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是
( )
图8
A.AB2=BC·BD
B.AB2=AC·BD
C.AB·AD=BD·BC
D.AB·AD=AD·CD
12.如图9,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B= °.?
图9
13.如图10,在△ABC中,E为BC上一点,CF⊥AB于点F,ED⊥AB于点D,G为AC边上一点,∠1=∠2.求证:△AFG∽△ABC.
图10
14.如图11,AB⊥BC于点B,DC⊥BC于点C,AB=4,DC=6,BC=14,点P在BC上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长.
图11
15.如图12,在△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从点C出发以1cm/s的速度向点A移动,当其中一点到达终点时,另一点也随之停止移动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB?
图12
16.从三角形(不是等腰三角形)的一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图13①,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB= °;?
图13
(2)如图②,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
答案
1.∠B AC ∽
2.B
3. 2
4.(1)AC AB (2)∠C ∠B
5.B [解析]
设△DEF的最长边的长为x
cm.∵△ABC∽△DEF,AB=6
cm,BC=4
cm,AC=9
cm,△DEF的最短边的长为8
cm,∴8∶4=x∶9,解得x=18,∴最长边的长为18
cm.
6.A [解析]
∵BE=3,CE=2,∴BC=BE+CE=5.∵△ABC∽△DEB,∴==,∴=.
7.D [解析]
因为△ABC∽△EDF,所以∠BAC=∠DEF.又∠DEF=90°+45°=135°,所以∠BAC=135°.
8.解:在△ABC中,∠A=180°-∠B-∠C=180°-75°-45°=60°.∵△DEF∽△ABC,∴∠D=∠A=60°,∠E=∠B=75°,=,∴=,∴DF=.
9.AFD EAB
10.解:在Rt△ABC中,∵AC=4,BC=3,∴AB=5.∵DE⊥AC,∠C=90°,∴DE∥BC,∴△ADE∽△ABC,∴=.∵DE=DB,∴DE=5-AD,∴=,解得AD=.故AD的长为.
11.A
12.30 [解析]
由作图可知,AD平分∠CAB,∴∠CAD=∠DAB.∵△DAC∽△ABC,∴∠CAD=∠B,∴∠CAB=2∠B.∵∠CAB+∠B=90°,∴3∠B=90°,∴∠B=30°.
13.证明:∵CF⊥AB,ED⊥AB,∴∠AFC=∠ADE=90°,∴∠2+∠AFG=∠1+∠B=90°.又∵∠1=∠2,∴∠AFG=∠B,∴FG∥BC,∴△AFG∽△ABC.
14.解:(1)当△ABP∽△PCD时,=,则=,解得BP=2或BP=12;
(2)当△ABP∽△DCP时,=,则=,解得BP=5.6.综上可得,当PB的长为2或12或5.6时,两三角形相似.
15.解:设经过t
s时,PQ∥AB,则BP=2t
cm,QC=t
cm,PC=(4-2t)cm.根据题意,得Rt△ABC∽Rt△QPC,所以=,即=,解得t=1.2.经检验,t=1.2是所列分式方程的解.由于点P的移动速度为2
cm/s,点Q的移动速度为1
cm/s,因此t的取值范围为0≤t≤2,所以t=1.2满足题目要求.答:经过1.2
s时,PQ∥AB.
16.解:(1)96 [解析]
当AD=CD时,∠ACD=∠A=48°.∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°.
(2)由已知,得AD=AC=2.∵△BAC∽△BCD,∴=.设BD=x,则()2=x(x+2).∵x>0,∴x=
-1.∵△BCD∽△BAC,∴==,∴CD=×2=-.故完美分割线CD的长为-.
【基础练习】
知识点
1 相似三角形的相关定义
1.如图1所示,D是△ABC的边AB上的一点,当∠ADC=∠ACB,∠ACD= ,∠A=∠A,==时,△ADC △ACB.?
图1
2.
下列说法中,错误的是
( )
A.两个全等三角形一定是相似三角形
B.两个等腰三角形一定相似
C.两个等边三角形一定相似
D.两个等腰直角三角形一定相似
3.若△ABC∽△DEF,AB=4cm,DE=8cm,则△ABC与△DEF的相似比为 ,△DEF与△ABC的相似比为 .?
知识点
2 相似三角形的应用
4.如图2,△ADE∽△ACB,则
图2
(1)==;
(2)∠ADE= ,∠AED= .?
5.已知△ABC∽△DEF,AB=6cm,BC=4cm,AC=9cm,且△DEF的最短边的长为8cm,则最长边的长为
( )
A.16cm
B.18cm
C.4.5cm
D.13cm
6.如图3,已知△ABC∽△DEB,BE=3,CE=2,则的值为
( )
图3
A.
B.
C.
D.
7.如图4,在正方形网格中有两个相似三角形△ABC和△DEF,则∠BAC的度数为
( )
图4
A.105°
B.115°
C.125°
D.135°
8.如图5,△DEF∽△ABC,求∠D和∠E的大小以及DF的长.
图5
知识点
3 利用平行线判定三角形相似
9.如图6,点F在平行四边形ABCD的边CD上,射线AF交BC的延长线于点E.
图6
∵AD∥BC,∴△EFC∽△ .?
∵AB∥CD,∴△EFC∽△ .?
10.如图7,在Rt△ABC中,∠C=90°.若AC=4,BC=3,DE⊥AC于点E,且DE=DB,求AD的长.
图7
【能力提升】
11.如图8,在△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是
( )
图8
A.AB2=BC·BD
B.AB2=AC·BD
C.AB·AD=BD·BC
D.AB·AD=AD·CD
12.如图9,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B= °.?
图9
13.如图10,在△ABC中,E为BC上一点,CF⊥AB于点F,ED⊥AB于点D,G为AC边上一点,∠1=∠2.求证:△AFG∽△ABC.
图10
14.如图11,AB⊥BC于点B,DC⊥BC于点C,AB=4,DC=6,BC=14,点P在BC上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长.
图11
15.如图12,在△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从点C出发以1cm/s的速度向点A移动,当其中一点到达终点时,另一点也随之停止移动.若动点P,Q同时出发,则经过多少秒时,PQ∥AB?
图12
16.从三角形(不是等腰三角形)的一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图13①,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB= °;?
图13
(2)如图②,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
答案
1.∠B AC ∽
2.B
3. 2
4.(1)AC AB (2)∠C ∠B
5.B [解析]
设△DEF的最长边的长为x
cm.∵△ABC∽△DEF,AB=6
cm,BC=4
cm,AC=9
cm,△DEF的最短边的长为8
cm,∴8∶4=x∶9,解得x=18,∴最长边的长为18
cm.
6.A [解析]
∵BE=3,CE=2,∴BC=BE+CE=5.∵△ABC∽△DEB,∴==,∴=.
7.D [解析]
因为△ABC∽△EDF,所以∠BAC=∠DEF.又∠DEF=90°+45°=135°,所以∠BAC=135°.
8.解:在△ABC中,∠A=180°-∠B-∠C=180°-75°-45°=60°.∵△DEF∽△ABC,∴∠D=∠A=60°,∠E=∠B=75°,=,∴=,∴DF=.
9.AFD EAB
10.解:在Rt△ABC中,∵AC=4,BC=3,∴AB=5.∵DE⊥AC,∠C=90°,∴DE∥BC,∴△ADE∽△ABC,∴=.∵DE=DB,∴DE=5-AD,∴=,解得AD=.故AD的长为.
11.A
12.30 [解析]
由作图可知,AD平分∠CAB,∴∠CAD=∠DAB.∵△DAC∽△ABC,∴∠CAD=∠B,∴∠CAB=2∠B.∵∠CAB+∠B=90°,∴3∠B=90°,∴∠B=30°.
13.证明:∵CF⊥AB,ED⊥AB,∴∠AFC=∠ADE=90°,∴∠2+∠AFG=∠1+∠B=90°.又∵∠1=∠2,∴∠AFG=∠B,∴FG∥BC,∴△AFG∽△ABC.
14.解:(1)当△ABP∽△PCD时,=,则=,解得BP=2或BP=12;
(2)当△ABP∽△DCP时,=,则=,解得BP=5.6.综上可得,当PB的长为2或12或5.6时,两三角形相似.
15.解:设经过t
s时,PQ∥AB,则BP=2t
cm,QC=t
cm,PC=(4-2t)cm.根据题意,得Rt△ABC∽Rt△QPC,所以=,即=,解得t=1.2.经检验,t=1.2是所列分式方程的解.由于点P的移动速度为2
cm/s,点Q的移动速度为1
cm/s,因此t的取值范围为0≤t≤2,所以t=1.2满足题目要求.答:经过1.2
s时,PQ∥AB.
16.解:(1)96 [解析]
当AD=CD时,∠ACD=∠A=48°.∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°.
(2)由已知,得AD=AC=2.∵△BAC∽△BCD,∴=.设BD=x,则()2=x(x+2).∵x>0,∴x=
-1.∵△BCD∽△BAC,∴==,∴CD=×2=-.故完美分割线CD的长为-.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
