2021-2022学年冀教版九年级数学上册25.4 相似三角形的判定 同步辅优训练(word解析版)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册25.4 相似三角形的判定 同步辅优训练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 288.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《25.4相似三角形的判定》
同步优生辅导训练(附答案)
一.选择题
1.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.=
D.=
2.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.=
B.=
C.=
D.=
3.如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
A.0个
B.1个
C.2个
D.3个
4.如图,在△ABC中,CE⊥AB于点E,BF⊥AC于点F,则图中相似三角形共有( )
A.5对
B.6对
C.7对
D.8对
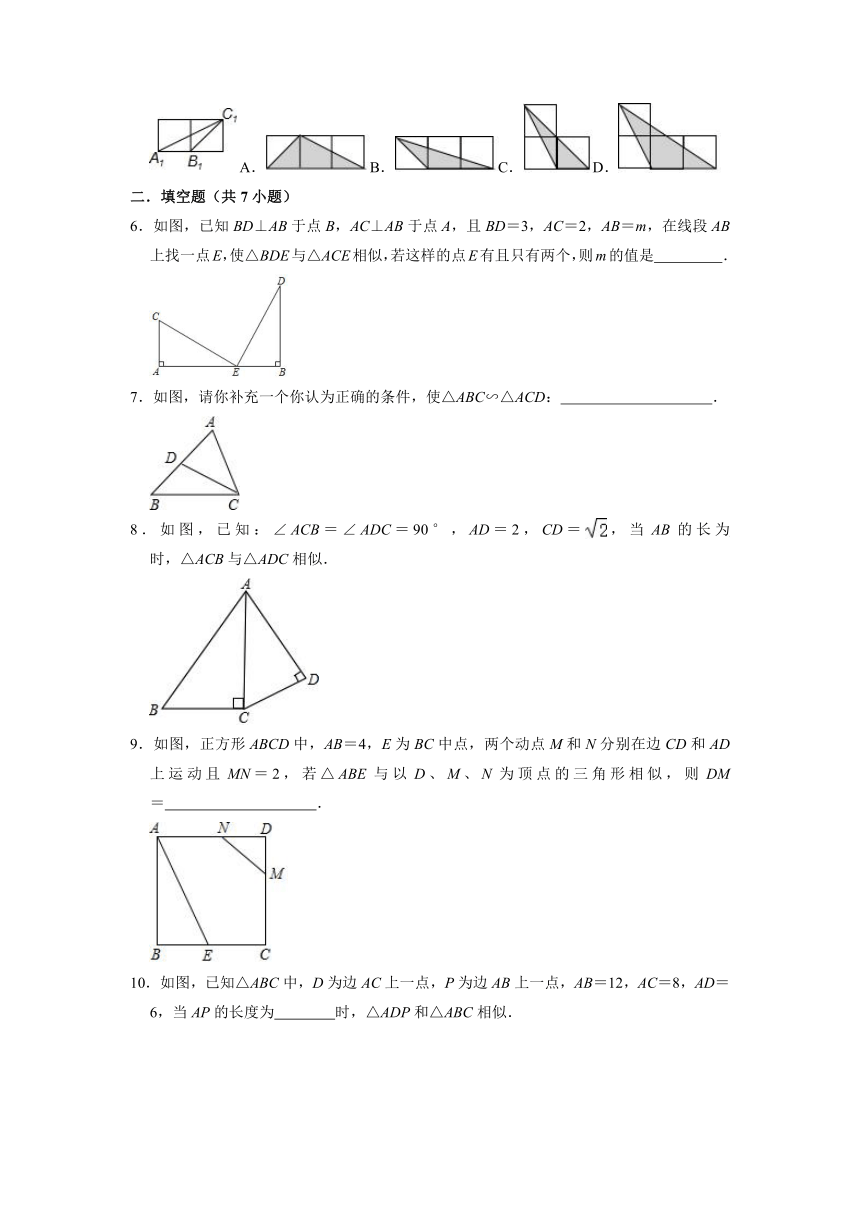
5.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
A.B.C.D.
二.填空题(共7小题)
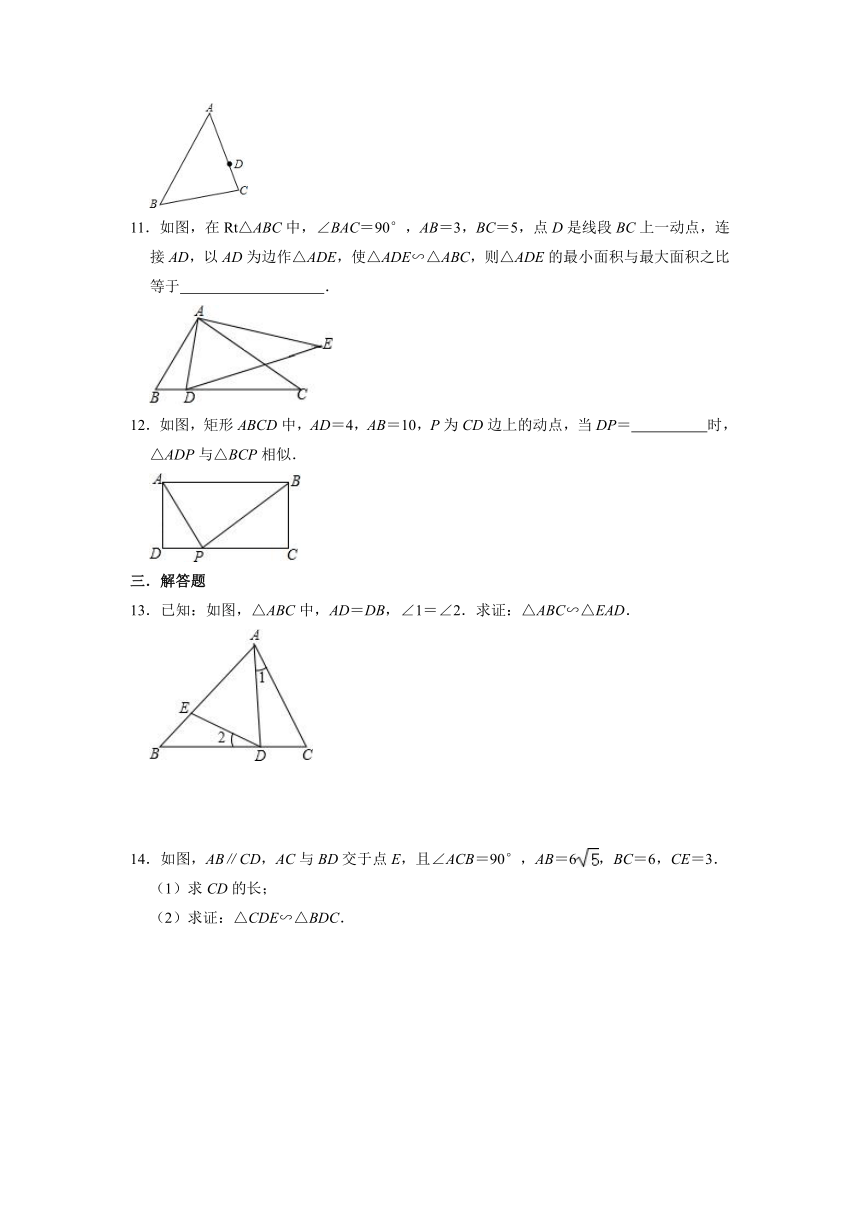
6.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是
.
7.如图,请你补充一个你认为正确的条件,使△ABC∽△ACD:
.
8.如图,已知:∠ACB=∠ADC=90°,AD=2,CD=,当AB的长为
时,△ACB与△ADC相似.
9.如图,正方形ABCD中,AB=4,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=2,若△ABE与以D、M、N为顶点的三角形相似,则DM=
.
10.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为
时,△ADP和△ABC相似.
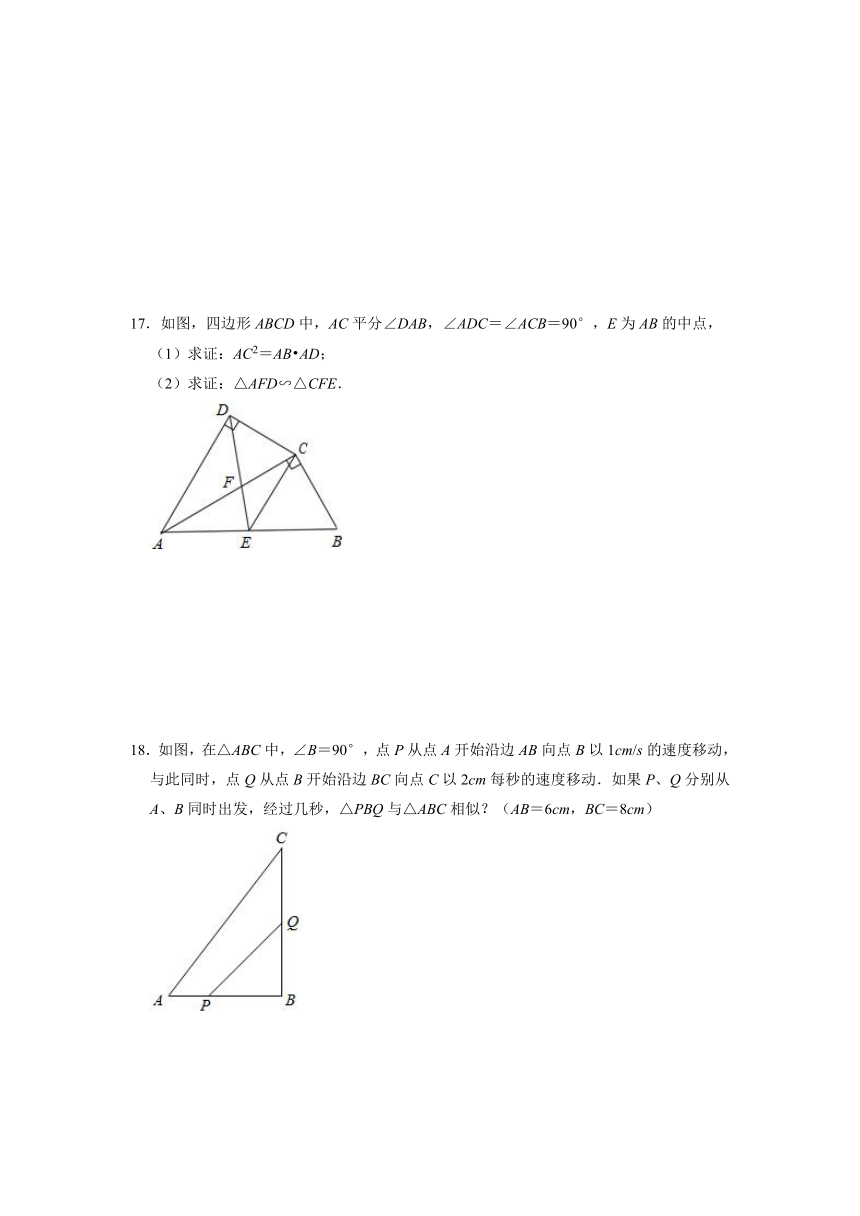
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点D是线段BC上一动点,连接AD,以AD为边作△ADE,使△ADE∽△ABC,则△ADE的最小面积与最大面积之比等于
.
12.如图,矩形ABCD中,AD=4,AB=10,P为CD边上的动点,当DP=
时,△ADP与△BCP相似.
三.解答题
13.已知:如图,△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
14.如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
15.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE?BF=EF?BC.
16.如图,锐角三角形ABC中,CD,BE分别是AB,AC边上的高,垂足为D,E.
(1)证明:△ACD∽△ABE.
(2)若将D,E连接起来,则△AED与△ABC能相似吗?说说你的理由.
17.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB?AD;
(2)求证:△AFD∽△CFE.
18.如图,在△ABC中,∠B=90°,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm每秒的速度移动.如果P、Q分别从A、B同时出发,经过几秒,△PBQ与△ABC相似?(AB=6cm,BC=8cm)
19.如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC=
,BC=
;
(2)判断△ABC与△DEF是否相似?并证明你的结论.
20.如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,
(Ⅰ)证明:△ABD≌△BCE;
(Ⅱ)证明:△ABE∽△FAE;
(Ⅲ)若AF=7,DF=1,求BD的长.
21.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.
参考答案
1.解:A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
C、当=时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
D、无法得到△ABP∽△ACB,故此选项符合题意.
故选:D.
2.解:∵∠BAC=∠D,,
∴△ABC∽△DEA.
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴△AEF∽△CBF,△AEF∽△DEC,
∴与△AEF相似的三角形有2个.
故选:C.
4.解:图中有△ABF∽△ACE,△BPE∽△CPF,△CPF∽△CAE,△CPF∽△ABF,△BPE∽△BFA,△BPE∽△CAE,△AEF∽△ACB,△EPF∽△BPC,8对三角形相似.
故选:D.
5.解:因为△A1B1C1中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,
故选:B.
6.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
当∠ACE=∠BDE时,△ACE∽△BDE,
∴==,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,即AE×BE=AC×BD=2×3=6②,
由①②得:BE2=6,
解得:BE=3,
∴AE=2,
∴AB=AE+BE=5,即m=5;
当AE=2时,BE=3,两个三角形相似;
当AE=3时,BE=2,两个三角形全等,符合题目要求;
设AE=x,则BE=m﹣x,
∴x:3=2:(m﹣x),
整理得:x2﹣mx+6=0,
方程有唯一解时,△=m2﹣24=0,
解得:m=±2(负值舍去),
∴m=2;
当m=2时,
AE:BE=2:3时,两个三角形相似;
AE=BE=时,两个三角形相似;同样是两个点可以满足要求;
综上所述,△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是5或2;
故答案为:5或2.
7.解:
①∵∠DAC=∠CAB,
又∵∠ADC=∠ACB,
∴△ADC∽△ACB;
②∵∠ACD=∠B,∠DAC=∠CAB,
∴△ADC∽△ACB;
③∵∠DAC=∠CAB,AC2=AD?AB,
∴△ADC∽△ACB.
8.解:∵AD=2,CD=,
∴AC==.
要使这两个直角三角形相似,有两种情况:(1)当Rt△ABC∽Rt△ACD时,有,∴AB=3;
(2)当Rt△ACB∽Rt△CDA时,有,∴AB=3.
即当AB的长为3或3时,这两个直角三角形相似.
故答案为:3或3.
9.解:∵正方形ABCD中,AB=4,E为BC中点,
∴BE=2,
由勾股定理得,AE==2,
当△ABE∽△MDN时,=,即=,
解得,DM=,
同理,当△ABE∽△NDM时,DM=,
∴DM为或,
故答案是:或.
10.解:当△ADP∽△ACB时,
∴=,
∴=,
解得:AP=9,
当△ADP∽△ABC时,
∴=,
∴=,
解得:AP=4,
∴当AP的长度为4或9时,△ADP和△ABC相似.
故答案为:4或9.
11.解:∵在Rt△ABC中,∠BAC=90°,AB=3,BC=5,
∴AC=4,
当AD⊥BC时,△ADE的面积最小,
∴AD===,
∵△ADE∽△ABC,
∴=,
∴=,
∴AE=,
∴△ADE的最小面积=×=;
当D与C重合时,△ADE的面积最大,
∵△ADE∽△ABC,
∴=,
∴=,
∴AE=,
∴△ADE的最大面积==,
∴△ADE的最小面积与最大面积之比==,
故答案为:.
12.解:①当△APD∽△PBC时,
,
即,
解得:PD=2或PD=8;
②当△PAD∽△PBC时,
,
即=,
解得:DP=5.
综上所述,DP的长度是2或8或5.
故答案是:2或8或5.
13.证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
14.(1)解:∵∠ACB=90°AB=6,BC=6,
∴AC==12;
∴AE=AC﹣CE=9,
∵AB∥CD,
∴△CDE∽△ABE;
∴,
∴CD===2,
(2)证明:∵∠ACB=90°,CE=3,BC=6,
∴BE==3,
∵AB∥CD,
∴△CDE∽△ABE,
∴,
∴DE=,
∴BD=4,
∵,,
∴,
∵∠D=∠D,
∴△CDE∽△BDC.
15.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)如图,连接DE,
∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE?BF=EF?BC
16.证明:(1)∵CD,BE分别是AB,AC边上的高,
∴∠ADC=∠AEB=90°.
∵∠A=∠A,
∴△ACD∽△ABE.
(2)连接DE,
∵△ACD∽△ABE,
∴AD:AE=AC:AB,
∴AD:AC=AE:AB,
∵∠A=∠A,
∴△AED∽△ABC.
17.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB?AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
18.解:设经过y秒后,以
P、Q、B三点为顶点的三角形与△ABC相似:
则AP=ycm,BQ=2ycm,
∴BP=AB﹣AP=(6﹣y)cm,
①若△PBQ∽△ABC,则有,即,
解得:y=;
②若△QBP∽△ABC,则有,即,
解得:y=.
答:经过或秒后,以
P、Q、B三点为顶点的三角形与△ABC相似.
19.(1)解:∠ABC=90°+45°=135°,
BC===2;
故答案为:135°;2.
(2)△ABC∽△DEF.
证明:∵在4×4的正方形方格中,
∠ABC=135°,∠DEF=90°+45°=135°,
∴∠ABC=∠DEF.
∵AB=2,BC=2,FE=2,DE=
∴==,==.
∴△ABC∽△DEF.
20.解:(Ⅰ)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE,
在△ABD与△BCE中
,
∴△ABD≌△BCE(SAS);
(Ⅱ)由(1)得:∠BAD=∠CBE,
又∵∠ABC=∠BAC,
∴∠ABE=∠EAF,
又∵∠AEF=∠BEA,
∴△AEF∽△BEA;
(Ⅲ)∵∠BAD=∠CBE,∠BDA=∠FDB,
∴△ABD∽△BFD,
∴,
∴BD2=AD?DF=(AF+DF)?DF=8,
∴BD=2.
21.(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴,
∴,
∴CD=;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFE,
∴AF=AB,
∴AD=AF+DF=AB+CD.
同步优生辅导训练(附答案)
一.选择题
1.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.=
D.=
2.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.=
B.=
C.=
D.=
3.如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
A.0个
B.1个
C.2个
D.3个
4.如图,在△ABC中,CE⊥AB于点E,BF⊥AC于点F,则图中相似三角形共有( )
A.5对
B.6对
C.7对
D.8对
5.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
A.B.C.D.
二.填空题(共7小题)
6.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是
.
7.如图,请你补充一个你认为正确的条件,使△ABC∽△ACD:
.
8.如图,已知:∠ACB=∠ADC=90°,AD=2,CD=,当AB的长为
时,△ACB与△ADC相似.
9.如图,正方形ABCD中,AB=4,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=2,若△ABE与以D、M、N为顶点的三角形相似,则DM=
.
10.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为
时,△ADP和△ABC相似.
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点D是线段BC上一动点,连接AD,以AD为边作△ADE,使△ADE∽△ABC,则△ADE的最小面积与最大面积之比等于
.
12.如图,矩形ABCD中,AD=4,AB=10,P为CD边上的动点,当DP=
时,△ADP与△BCP相似.
三.解答题
13.已知:如图,△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
14.如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
15.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE?BF=EF?BC.
16.如图,锐角三角形ABC中,CD,BE分别是AB,AC边上的高,垂足为D,E.
(1)证明:△ACD∽△ABE.
(2)若将D,E连接起来,则△AED与△ABC能相似吗?说说你的理由.
17.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB?AD;
(2)求证:△AFD∽△CFE.
18.如图,在△ABC中,∠B=90°,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm每秒的速度移动.如果P、Q分别从A、B同时出发,经过几秒,△PBQ与△ABC相似?(AB=6cm,BC=8cm)
19.如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC=
,BC=
;
(2)判断△ABC与△DEF是否相似?并证明你的结论.
20.如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,
(Ⅰ)证明:△ABD≌△BCE;
(Ⅱ)证明:△ABE∽△FAE;
(Ⅲ)若AF=7,DF=1,求BD的长.
21.如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.
参考答案
1.解:A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
C、当=时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
D、无法得到△ABP∽△ACB,故此选项符合题意.
故选:D.
2.解:∵∠BAC=∠D,,
∴△ABC∽△DEA.
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴△AEF∽△CBF,△AEF∽△DEC,
∴与△AEF相似的三角形有2个.
故选:C.
4.解:图中有△ABF∽△ACE,△BPE∽△CPF,△CPF∽△CAE,△CPF∽△ABF,△BPE∽△BFA,△BPE∽△CAE,△AEF∽△ACB,△EPF∽△BPC,8对三角形相似.
故选:D.
5.解:因为△A1B1C1中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,
故选:B.
6.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
当∠ACE=∠BDE时,△ACE∽△BDE,
∴==,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,即AE×BE=AC×BD=2×3=6②,
由①②得:BE2=6,
解得:BE=3,
∴AE=2,
∴AB=AE+BE=5,即m=5;
当AE=2时,BE=3,两个三角形相似;
当AE=3时,BE=2,两个三角形全等,符合题目要求;
设AE=x,则BE=m﹣x,
∴x:3=2:(m﹣x),
整理得:x2﹣mx+6=0,
方程有唯一解时,△=m2﹣24=0,
解得:m=±2(负值舍去),
∴m=2;
当m=2时,
AE:BE=2:3时,两个三角形相似;
AE=BE=时,两个三角形相似;同样是两个点可以满足要求;
综上所述,△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是5或2;
故答案为:5或2.
7.解:
①∵∠DAC=∠CAB,
又∵∠ADC=∠ACB,
∴△ADC∽△ACB;
②∵∠ACD=∠B,∠DAC=∠CAB,
∴△ADC∽△ACB;
③∵∠DAC=∠CAB,AC2=AD?AB,
∴△ADC∽△ACB.
8.解:∵AD=2,CD=,
∴AC==.
要使这两个直角三角形相似,有两种情况:(1)当Rt△ABC∽Rt△ACD时,有,∴AB=3;
(2)当Rt△ACB∽Rt△CDA时,有,∴AB=3.
即当AB的长为3或3时,这两个直角三角形相似.
故答案为:3或3.
9.解:∵正方形ABCD中,AB=4,E为BC中点,
∴BE=2,
由勾股定理得,AE==2,
当△ABE∽△MDN时,=,即=,
解得,DM=,
同理,当△ABE∽△NDM时,DM=,
∴DM为或,
故答案是:或.
10.解:当△ADP∽△ACB时,
∴=,
∴=,
解得:AP=9,
当△ADP∽△ABC时,
∴=,
∴=,
解得:AP=4,
∴当AP的长度为4或9时,△ADP和△ABC相似.
故答案为:4或9.
11.解:∵在Rt△ABC中,∠BAC=90°,AB=3,BC=5,
∴AC=4,
当AD⊥BC时,△ADE的面积最小,
∴AD===,
∵△ADE∽△ABC,
∴=,
∴=,
∴AE=,
∴△ADE的最小面积=×=;
当D与C重合时,△ADE的面积最大,
∵△ADE∽△ABC,
∴=,
∴=,
∴AE=,
∴△ADE的最大面积==,
∴△ADE的最小面积与最大面积之比==,
故答案为:.
12.解:①当△APD∽△PBC时,
,
即,
解得:PD=2或PD=8;
②当△PAD∽△PBC时,
,
即=,
解得:DP=5.
综上所述,DP的长度是2或8或5.
故答案是:2或8或5.
13.证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
14.(1)解:∵∠ACB=90°AB=6,BC=6,
∴AC==12;
∴AE=AC﹣CE=9,
∵AB∥CD,
∴△CDE∽△ABE;
∴,
∴CD===2,
(2)证明:∵∠ACB=90°,CE=3,BC=6,
∴BE==3,
∵AB∥CD,
∴△CDE∽△ABE,
∴,
∴DE=,
∴BD=4,
∵,,
∴,
∵∠D=∠D,
∴△CDE∽△BDC.
15.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)如图,连接DE,
∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE?BF=EF?BC
16.证明:(1)∵CD,BE分别是AB,AC边上的高,
∴∠ADC=∠AEB=90°.
∵∠A=∠A,
∴△ACD∽△ABE.
(2)连接DE,
∵△ACD∽△ABE,
∴AD:AE=AC:AB,
∴AD:AC=AE:AB,
∵∠A=∠A,
∴△AED∽△ABC.
17.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB?AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
18.解:设经过y秒后,以
P、Q、B三点为顶点的三角形与△ABC相似:
则AP=ycm,BQ=2ycm,
∴BP=AB﹣AP=(6﹣y)cm,
①若△PBQ∽△ABC,则有,即,
解得:y=;
②若△QBP∽△ABC,则有,即,
解得:y=.
答:经过或秒后,以
P、Q、B三点为顶点的三角形与△ABC相似.
19.(1)解:∠ABC=90°+45°=135°,
BC===2;
故答案为:135°;2.
(2)△ABC∽△DEF.
证明:∵在4×4的正方形方格中,
∠ABC=135°,∠DEF=90°+45°=135°,
∴∠ABC=∠DEF.
∵AB=2,BC=2,FE=2,DE=
∴==,==.
∴△ABC∽△DEF.
20.解:(Ⅰ)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE,
在△ABD与△BCE中
,
∴△ABD≌△BCE(SAS);
(Ⅱ)由(1)得:∠BAD=∠CBE,
又∵∠ABC=∠BAC,
∴∠ABE=∠EAF,
又∵∠AEF=∠BEA,
∴△AEF∽△BEA;
(Ⅲ)∵∠BAD=∠CBE,∠BDA=∠FDB,
∴△ABD∽△BFD,
∴,
∴BD2=AD?DF=(AF+DF)?DF=8,
∴BD=2.
21.(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴,
∴,
∴CD=;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFE,
∴AF=AB,
∴AD=AF+DF=AB+CD.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
