2021-2022学年冀教版九年级数学上册25.6相似三角形的应用 同步能力提高训练(word解析版)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册25.6相似三角形的应用 同步能力提高训练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 312.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《25.6相似三角形的应用》
同步能力提高训练(附答案)
一.选择题
1.下列图形不是相似图形的是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
2.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB是( )
A.4米
B.4.5米
C.5米
D.5.5米
3.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度约为( )
A.39米
B.30米
C.24米
D.15米
4.如图,在一块斜边长60cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若CD:CB=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.202.5cm2
B.320cm2
C.400cm2
D.405cm2
5.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米
B.减小1.5米
C.增大3.5米
D.减小3.5米
6.小明身高为1.6米,他在距路灯5米处的位置发现自己的影长为1米,他在向前走距离路灯为7米时,他的影长将( )
A.增长0.4米
B.减少0.4米
C.增长1.4米
D.减少1.4米
7.在小孔成像问题中,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A.
B.
C.2倍
D.3倍
二.填空题
8.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.8米,BD=1米,BE=0.2米,那么AC为
米.
9.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子高CD为2m,那么这棵大树高
m.
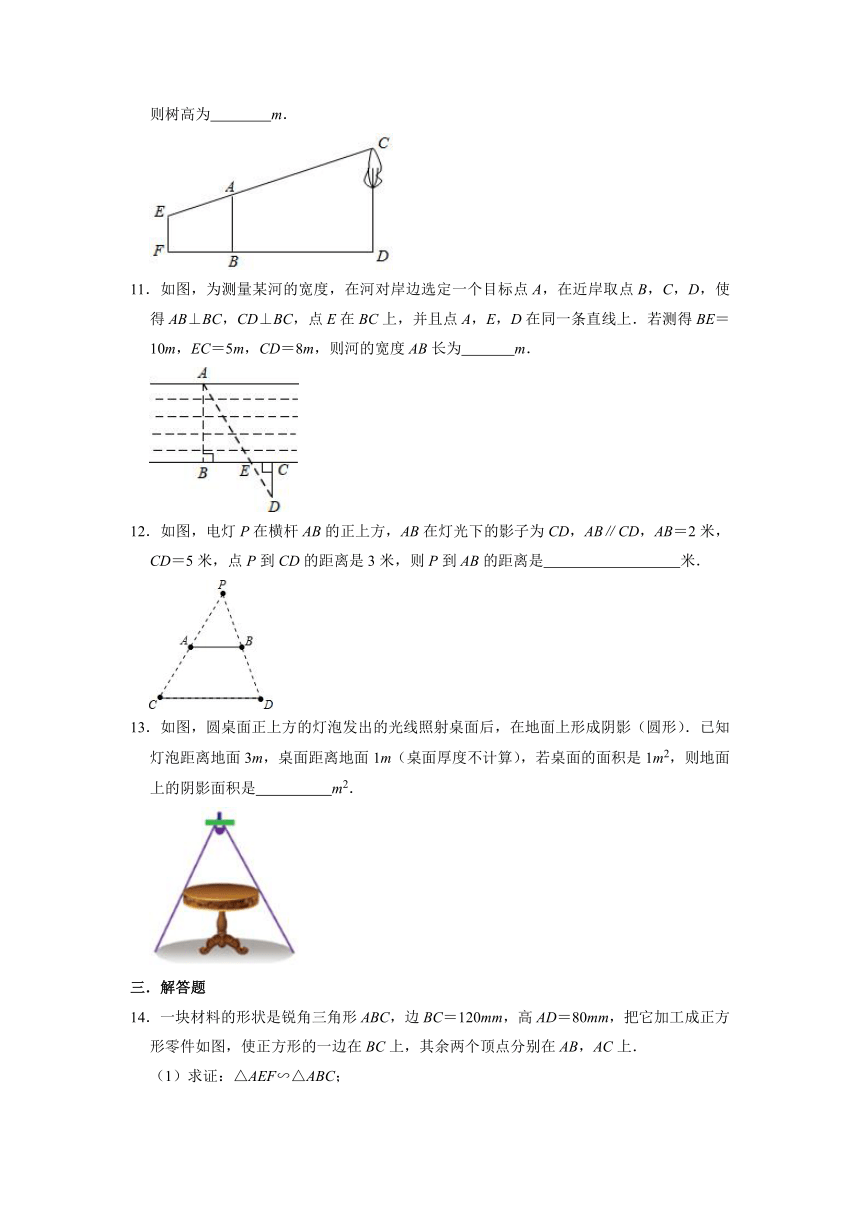
10.如图,为了测量一棵树CD的高度,测量者在B处立了一根高为2.5m的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上,若测得BD=7m,FB=3m,EF=1.6m,则树高为
m.
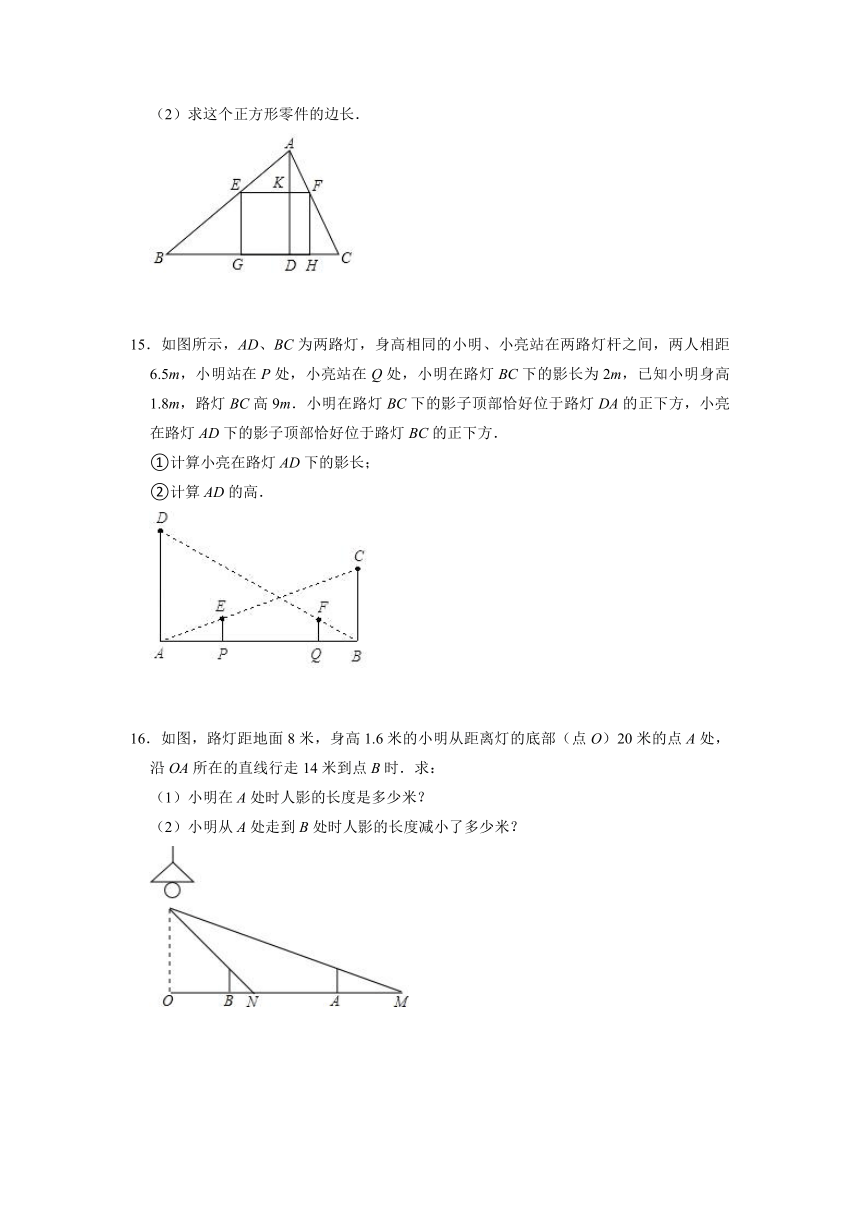
11.如图,为测量某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=10m,EC=5m,CD=8m,则河的宽度AB长为
m.
12.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2米,CD=5米,点P到CD的距离是3米,则P到AB的距离是
米.
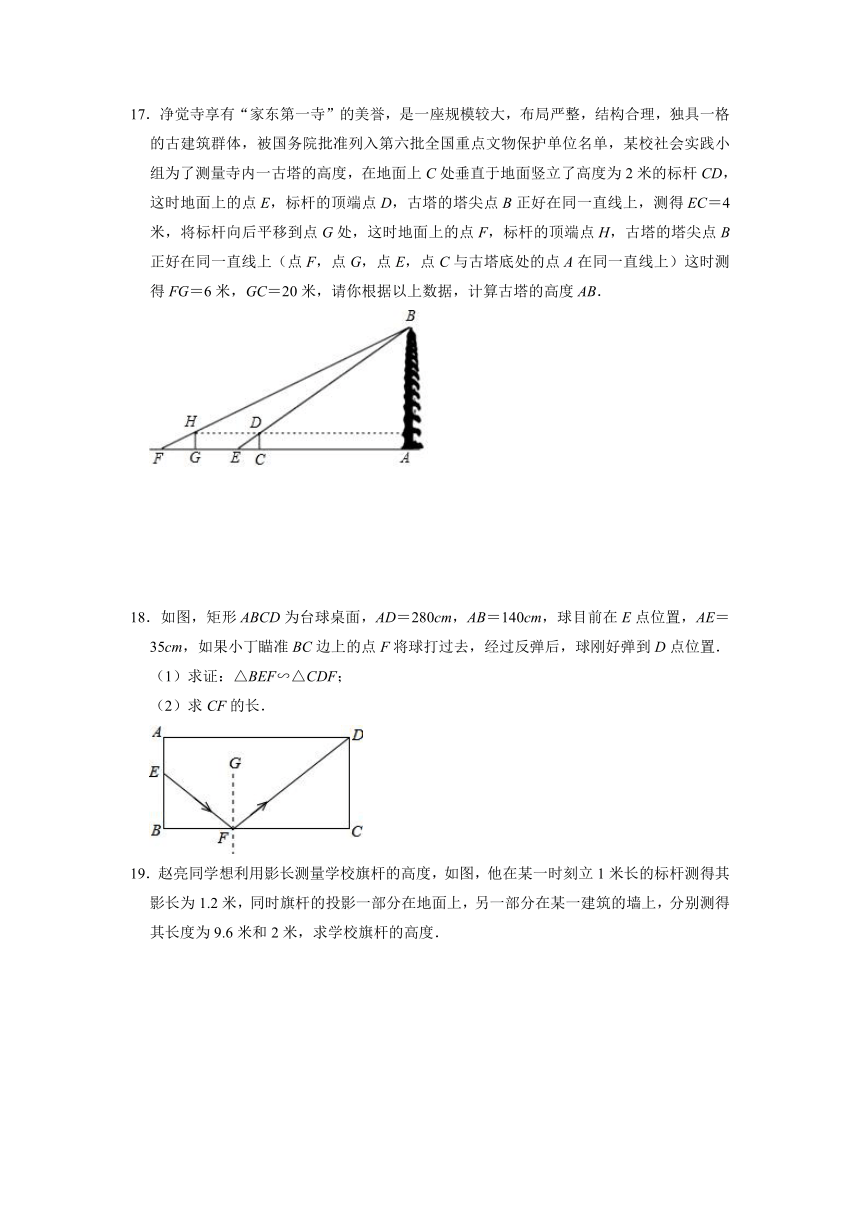
13.如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面3m,桌面距离地面1m(桌面厚度不计算),若桌面的面积是1m2,则地面上的阴影面积是
m2.
三.解答题
14.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长.
15.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯BC下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
①计算小亮在路灯AD下的影长;
②计算AD的高.
16.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时.求:
(1)小明在A处时人影的长度是多少米?
(2)小明从A处走到B处时人影的长度减小了多少米?
17.净觉寺享有“家东第一寺”的美誉,是一座规模较大,布局严整,结构合理,独具一格的古建筑群体,被国务院批准列入第六批全国重点文物保护单位名单,某校社会实践小组为了测量寺内一古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上)这时测得FG=6米,GC=20米,请你根据以上数据,计算古塔的高度AB.
18.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
19.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.
20.小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与地面成30°角,且在此时测得1m杆的影长为2m,求电线杆的高度.
参考答案
1.解:A、同一张底片冲洗出来的两张大小不同的照片,是相似图形,不合题意;
B、用放大镜将一个细小物体图案放大过程中原有图案和放大图案,相似图形,不合题意;
C、某人的侧身照片和正面像,不是相似图形,符合题意;
D、大小不同的两张中国地图,相似图形,不合题意;
故选:C.
2.解:在△DEF和△DBC中,,
∴△DEF∽△DBC,
∴=,
即=,
解得:BC=4,
∵AC=1.5m,
∴AB=AC+BC=1.5+4=5.5m,
即树高5.5m.
故选:D.
3.解:根据题意,得到:△ABP∽△CDP.
即,
故CD=×AB=×1.5=39米;
那么该大厦的高度是39米.
故选:A.
4.解:
∵四边形CDEF为正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∵CD:CB=1:3,
∴==,
设AF=x,则AC=3x,EF=CF=2x,
∴BC=6x,
在Rt△ABC中,AB2=AC2+BC2,即602=(3x)2+(6x)2,
解得,x=4,
∴AC=12,BC=24,
∴剩余部分的面积=×24×12﹣8×8=400(cm2),
故选:C.
5.解:设小明在A处时影长为x,B处时影长为y.
∵AC∥OP,BD∥OP,
∴△ACM∽△OPM,△BDN∽△OPN,
∴,,
则,
∴x=5,
,
∴y=1.5,
∴x﹣y=3.5,
减少了3.5米.
故选:D.
6.解:设路灯距地面的高度是x米,
∵小明身高为1.6米,他在距路灯5米处的位置发现自己的影长为1米,
∴,
∴x=9.6,
设他在向前走距离路灯为7米时,他的影长为y米,
∵他在向前走距离路灯为7米,
∴,
∴y=1.4,
∴他的影长将增长0.4米,
故选:A.
7.解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴===(相似三角形的对应高的比等于相似比),
∴CD=AB,
故选:A.
8.解:∵BD⊥AB,AC⊥AB,
∴BD∥AC,
∴△ACE∽△BDE,
∴=,
∵AB=1.8米,BD=1米,BE=0.2米,
∴AE=AB﹣BE=1.6米,
∴=,
∴AC=8(米),
故答案为8.
9.解:如图所示,过D作DE⊥AB于E,
则BE=CD=2(m),DE=BC=5(m).
∵同一时刻物高和影长成正比,
∴=,
∴AE=7m,
∴AB=AE+BE=7+2=9(m),
即:这棵大树高为9m.
故答案为:9.
10.解:作EH⊥CD于H,交AB于G,如图,
则EG=BF=3m,GH=BD=7m,GB=HD=EF=1.6m,
所以AG=AB﹣GB=2.5﹣1.6=0.9(m),
∵AG∥CH,
∴△EAG∽△EHC,
∴=,即=,
解得:CH=3,
∴CD=CH+DH=4.6(m).
故答案为:4.6.
11.解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC(对顶角相等),
∴△ABE∽△DCE,
∴=,
即=,
解得AB=16m.
故答案为:16.
12.解:∵AB∥CD
∴△PAB∽△PCD
∴AB:CD=P到AB的距离:点P到CD的距离.
∴2:5=P到AB的距离:3
∴P到AB的距离为m,
故答案为.
13.解:如图设C,D分别是桌面和其地面影子的圆心,
∵CB∥AD,
∴△OBC∽△OAD
∴=,
∵OD=3,CD=1,
∴OC=OD﹣CD=2,
=
∴S阴影=2.25m2,
这样地面上阴影部分的面积为2.25m2;
故答案为:2.25.
14.(1)证明:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC.
(2)解:设这个正方形零件的边长是xmm,
∵EF∥BC,
∴=,
∴=,
解得x=48
答:这个正方形零件的边长是48mm.
15.解:①∵EP⊥AB,CB⊥AB,
∴∠EPA=∠CBA=90°
∵∠EAP=∠CAB,
∴△EAP∽△CAB
∴
∴
∴AB=10
BQ=10﹣2﹣6.5=1.5;
②∵FQ⊥AB,DA⊥AB,
∴∠FQB=∠DAB=90°
∵∠FBQ=∠DBA,
∴△BFQ∽△BDA
∴=
∴
∴DA=12.
16.解:(1)解:由题意AC∥OP,BD∥OP,
∴△ACM∽△OPM,
∴,
设AM=x,AC=1.6,OP=8,OM=OA+AM=20+x,
∴,
∴x=5,
∴小明在A处是的人影的长度是5米;
(2)∵BD∥OP,
∴△BDN∽△OPN,
∴,
∵OP=8,BD=1.6,OB=OA﹣AB=20﹣14=6,
设BN=y,ON=OB+y=6+y
∴,
∴y=1.5
∴x﹣y=5﹣1.5=3.5
∴影长减少了3.5米.
17.解:∵△EDC∽△EBA,
∴=,
∵△FHG∽△FBA,
∴=,
∵DC=HG,
∴=,
∴=,
∴CA=40(米),
∵=,
∴=,
∴AB=22(米),
答:古塔的高度AB为22米.
18.(1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴=,
设FC=xcm,则=,
解得:x=160,
答:CF的长为160cm.
19.解:作DE⊥AB于点E,
根据题意得:=,
=,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
20.解:如图,过D作DE⊥BC的延长线于E,连接AD并延长交BC的延长线于F,
∵CD=4米,CD与地面成30°角,
∴DE=CD=×4=2米,根据勾股定理得,CE===2米,
∵1米杆的影长为2米,
∴=,
∴EF=2DE=2×2=4米,
∴BF=BC+CE+EF=10+2+4=(14+2)米,
∵=,
∴AB=(14+2)=(7+)米.
答:电线杆的高度为(7+)m.
同步能力提高训练(附答案)
一.选择题
1.下列图形不是相似图形的是( )
A.同一张底片冲洗出来的两张大小不同的照片
B.用放大镜将一个细小物体图案放大过程中原有图案和放大图案
C.某人的侧身照片和正面照片
D.大小不同的两张中国地图
2.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB是( )
A.4米
B.4.5米
C.5米
D.5.5米
3.某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度约为( )
A.39米
B.30米
C.24米
D.15米
4.如图,在一块斜边长60cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若CD:CB=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.202.5cm2
B.320cm2
C.400cm2
D.405cm2
5.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米
B.减小1.5米
C.增大3.5米
D.减小3.5米
6.小明身高为1.6米,他在距路灯5米处的位置发现自己的影长为1米,他在向前走距离路灯为7米时,他的影长将( )
A.增长0.4米
B.减少0.4米
C.增长1.4米
D.减少1.4米
7.在小孔成像问题中,如图所示,若O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A.
B.
C.2倍
D.3倍
二.填空题
8.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.8米,BD=1米,BE=0.2米,那么AC为
米.
9.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子高CD为2m,那么这棵大树高
m.
10.如图,为了测量一棵树CD的高度,测量者在B处立了一根高为2.5m的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上,若测得BD=7m,FB=3m,EF=1.6m,则树高为
m.
11.如图,为测量某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=10m,EC=5m,CD=8m,则河的宽度AB长为
m.
12.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2米,CD=5米,点P到CD的距离是3米,则P到AB的距离是
米.
13.如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面3m,桌面距离地面1m(桌面厚度不计算),若桌面的面积是1m2,则地面上的阴影面积是
m2.
三.解答题
14.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长.
15.如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯BC下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
①计算小亮在路灯AD下的影长;
②计算AD的高.
16.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时.求:
(1)小明在A处时人影的长度是多少米?
(2)小明从A处走到B处时人影的长度减小了多少米?
17.净觉寺享有“家东第一寺”的美誉,是一座规模较大,布局严整,结构合理,独具一格的古建筑群体,被国务院批准列入第六批全国重点文物保护单位名单,某校社会实践小组为了测量寺内一古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上)这时测得FG=6米,GC=20米,请你根据以上数据,计算古塔的高度AB.
18.如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
19.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.
20.小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与地面成30°角,且在此时测得1m杆的影长为2m,求电线杆的高度.
参考答案
1.解:A、同一张底片冲洗出来的两张大小不同的照片,是相似图形,不合题意;
B、用放大镜将一个细小物体图案放大过程中原有图案和放大图案,相似图形,不合题意;
C、某人的侧身照片和正面像,不是相似图形,符合题意;
D、大小不同的两张中国地图,相似图形,不合题意;
故选:C.
2.解:在△DEF和△DBC中,,
∴△DEF∽△DBC,
∴=,
即=,
解得:BC=4,
∵AC=1.5m,
∴AB=AC+BC=1.5+4=5.5m,
即树高5.5m.
故选:D.
3.解:根据题意,得到:△ABP∽△CDP.
即,
故CD=×AB=×1.5=39米;
那么该大厦的高度是39米.
故选:A.
4.解:
∵四边形CDEF为正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∵CD:CB=1:3,
∴==,
设AF=x,则AC=3x,EF=CF=2x,
∴BC=6x,
在Rt△ABC中,AB2=AC2+BC2,即602=(3x)2+(6x)2,
解得,x=4,
∴AC=12,BC=24,
∴剩余部分的面积=×24×12﹣8×8=400(cm2),
故选:C.
5.解:设小明在A处时影长为x,B处时影长为y.
∵AC∥OP,BD∥OP,
∴△ACM∽△OPM,△BDN∽△OPN,
∴,,
则,
∴x=5,
,
∴y=1.5,
∴x﹣y=3.5,
减少了3.5米.
故选:D.
6.解:设路灯距地面的高度是x米,
∵小明身高为1.6米,他在距路灯5米处的位置发现自己的影长为1米,
∴,
∴x=9.6,
设他在向前走距离路灯为7米时,他的影长为y米,
∵他在向前走距离路灯为7米,
∴,
∴y=1.4,
∴他的影长将增长0.4米,
故选:A.
7.解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴===(相似三角形的对应高的比等于相似比),
∴CD=AB,
故选:A.
8.解:∵BD⊥AB,AC⊥AB,
∴BD∥AC,
∴△ACE∽△BDE,
∴=,
∵AB=1.8米,BD=1米,BE=0.2米,
∴AE=AB﹣BE=1.6米,
∴=,
∴AC=8(米),
故答案为8.
9.解:如图所示,过D作DE⊥AB于E,
则BE=CD=2(m),DE=BC=5(m).
∵同一时刻物高和影长成正比,
∴=,
∴AE=7m,
∴AB=AE+BE=7+2=9(m),
即:这棵大树高为9m.
故答案为:9.
10.解:作EH⊥CD于H,交AB于G,如图,
则EG=BF=3m,GH=BD=7m,GB=HD=EF=1.6m,
所以AG=AB﹣GB=2.5﹣1.6=0.9(m),
∵AG∥CH,
∴△EAG∽△EHC,
∴=,即=,
解得:CH=3,
∴CD=CH+DH=4.6(m).
故答案为:4.6.
11.解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC(对顶角相等),
∴△ABE∽△DCE,
∴=,
即=,
解得AB=16m.
故答案为:16.
12.解:∵AB∥CD
∴△PAB∽△PCD
∴AB:CD=P到AB的距离:点P到CD的距离.
∴2:5=P到AB的距离:3
∴P到AB的距离为m,
故答案为.
13.解:如图设C,D分别是桌面和其地面影子的圆心,
∵CB∥AD,
∴△OBC∽△OAD
∴=,
∵OD=3,CD=1,
∴OC=OD﹣CD=2,
=
∴S阴影=2.25m2,
这样地面上阴影部分的面积为2.25m2;
故答案为:2.25.
14.(1)证明:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC.
(2)解:设这个正方形零件的边长是xmm,
∵EF∥BC,
∴=,
∴=,
解得x=48
答:这个正方形零件的边长是48mm.
15.解:①∵EP⊥AB,CB⊥AB,
∴∠EPA=∠CBA=90°
∵∠EAP=∠CAB,
∴△EAP∽△CAB
∴
∴
∴AB=10
BQ=10﹣2﹣6.5=1.5;
②∵FQ⊥AB,DA⊥AB,
∴∠FQB=∠DAB=90°
∵∠FBQ=∠DBA,
∴△BFQ∽△BDA
∴=
∴
∴DA=12.
16.解:(1)解:由题意AC∥OP,BD∥OP,
∴△ACM∽△OPM,
∴,
设AM=x,AC=1.6,OP=8,OM=OA+AM=20+x,
∴,
∴x=5,
∴小明在A处是的人影的长度是5米;
(2)∵BD∥OP,
∴△BDN∽△OPN,
∴,
∵OP=8,BD=1.6,OB=OA﹣AB=20﹣14=6,
设BN=y,ON=OB+y=6+y
∴,
∴y=1.5
∴x﹣y=5﹣1.5=3.5
∴影长减少了3.5米.
17.解:∵△EDC∽△EBA,
∴=,
∵△FHG∽△FBA,
∴=,
∵DC=HG,
∴=,
∴=,
∴CA=40(米),
∵=,
∴=,
∴AB=22(米),
答:古塔的高度AB为22米.
18.(1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴=,
设FC=xcm,则=,
解得:x=160,
答:CF的长为160cm.
19.解:作DE⊥AB于点E,
根据题意得:=,
=,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
20.解:如图,过D作DE⊥BC的延长线于E,连接AD并延长交BC的延长线于F,
∵CD=4米,CD与地面成30°角,
∴DE=CD=×4=2米,根据勾股定理得,CE===2米,
∵1米杆的影长为2米,
∴=,
∴EF=2DE=2×2=4米,
∴BF=BC+CE+EF=10+2+4=(14+2)米,
∵=,
∴AB=(14+2)=(7+)米.
答:电线杆的高度为(7+)m.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
