2021-2022学年冀教版九年级数学上册25.5相似三角形的性质 同步能力提高训练(word解析版)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册25.5相似三角形的性质 同步能力提高训练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 675.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《25.5相似三角形的性质》
同步能力提高训练(附答案)
一.选择题
1.如图,在平行四边形ABCD中,点E是边AD上的中点,EC交对角线BD于点F,则等于( )
A.
B.
C.
D.
2.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.
B.
C.
D.
3.如图,在△ABC中,DE∥BC,=2,记△ADE的面积为a,四边形DBCE的面积为b,则的值是( )
A.
B.
C.
D.
4.如图,在△ABC中,∠C=90°,AB=10,BC=8.E是AC边上一动点,过点E作EF∥AB交BC于点F,D为线段EF的中点,当BD平分∠ABC时,AE的长度是( )
A.
B.
C.
D.
5.如图△ABC中,点D、E分别在AB、AC上,且==,下列结论正确的是( )
A.DE:BC=1:2
B.△ADE与△ABC的面积比为1:3
C.△ADE与△ABC的周长比为1:2
D.DE∥BC
6.如图,D、E分别为△ABC的边AB、AC上的点,且DE∥BC,CD、BE相交于点O,BD=2AD.若△ODE的面积为1,则△BCE的面积为( )
A.6
B.8
C.10
D.12
7.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,则点A到直线DE的距离AF的长度为( )
A.
B.
C.2.5
D.
8.已知∠MAN=30°,点B在射线AM上,按以下步骤作图:
①分别以A,B为圆心,大于AB的长为半径画弧,两弧相交于P,Q两点;
②作直线PQ,交射线AN于点C,连接BC;
③以B为圆心,BA长为半径画弧,交射线AN于点D.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠BCD=60°
B.AB2=AD?AC
C.∠ABD=4∠CBA
D.AD=2AB
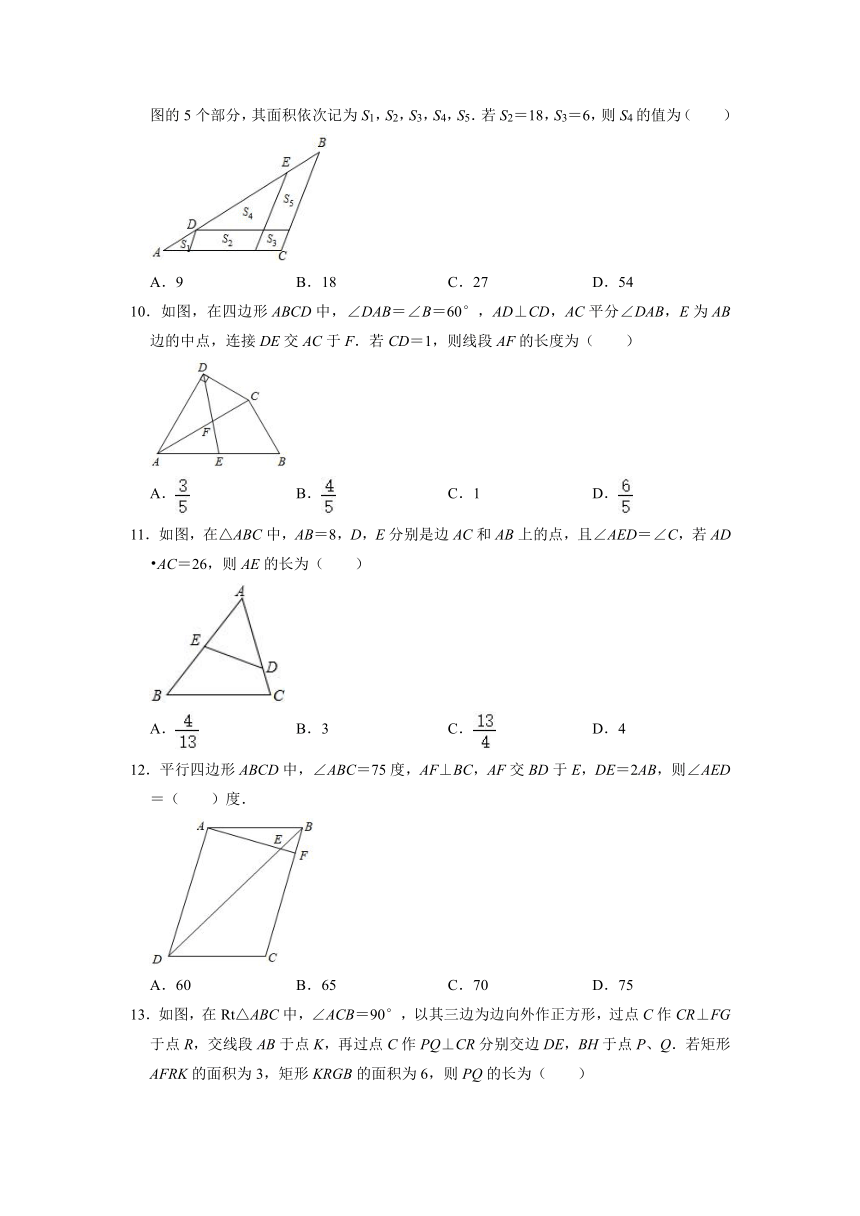
9.《几何原本》有一个图形:在△ABC中,D,E是边AB上的两点(AD<AE),且满足AD=BE.过点D,E分别作BC的平行线,过点D作AC的平行线,它们将△ABC分成如图的5个部分,其面积依次记为S1,S2,S3,S4,S5.若S2=18,S3=6,则S4的值为( )
A.9
B.18
C.27
D.54
10.如图,在四边形ABCD中,∠DAB=∠B=60°,AD⊥CD,AC平分∠DAB,E为AB边的中点,连接DE交AC于F.若CD=1,则线段AF的长度为( )
A.
B.
C.1
D.
11.如图,在△ABC中,AB=8,D,E分别是边AC和AB上的点,且∠AED=∠C,若AD?AC=26,则AE的长为( )
A.
B.3
C.
D.4
12.平行四边形ABCD中,∠ABC=75度,AF⊥BC,AF交BD于E,DE=2AB,则∠AED=( )度.
A.60
B.65
C.70
D.75
13.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,交线段AB于点K,再过点C作PQ⊥CR分别交边DE,BH于点P、Q.若矩形AFRK的面积为3,矩形KRGB的面积为6,则PQ的长为( )
A.4.5
B.5
C.3
D.3
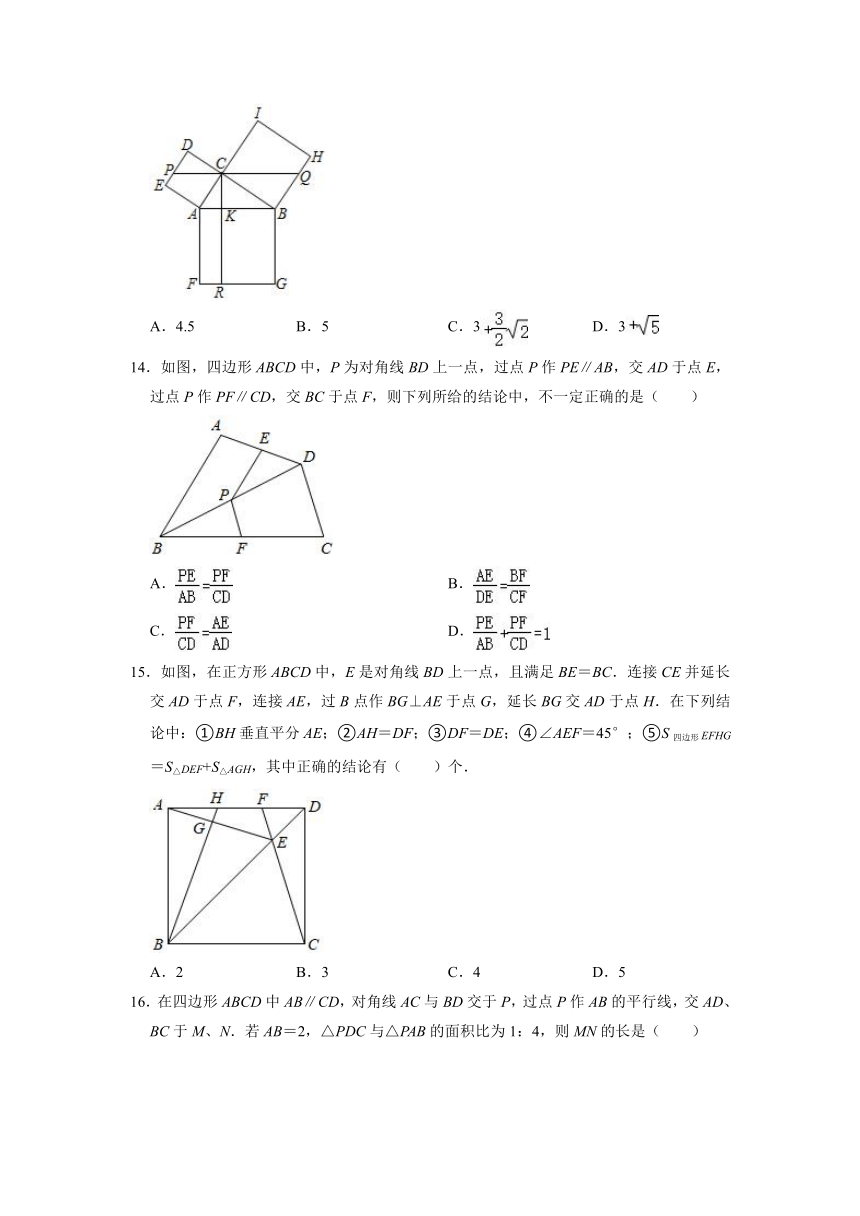
14.如图,四边形ABCD中,P为对角线BD上一点,过点P作PE∥AB,交AD于点E,过点P作PF∥CD,交BC于点F,则下列所给的结论中,不一定正确的是( )
A.
B.
C.
D.
15.如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:①BH垂直平分AE;②AH=DF;③DF=DE;④∠AEF=45°;⑤S四边形EFHG=S△DEF+S△AGH,其中正确的结论有( )个.
A.2
B.3
C.4
D.5
16.在四边形ABCD中AB∥CD,对角线AC与BD交于P,过点P作AB的平行线,交AD、BC于M、N.若AB=2,△PDC与△PAB的面积比为1:4,则MN的长是( )
A.
B.
C.
D.
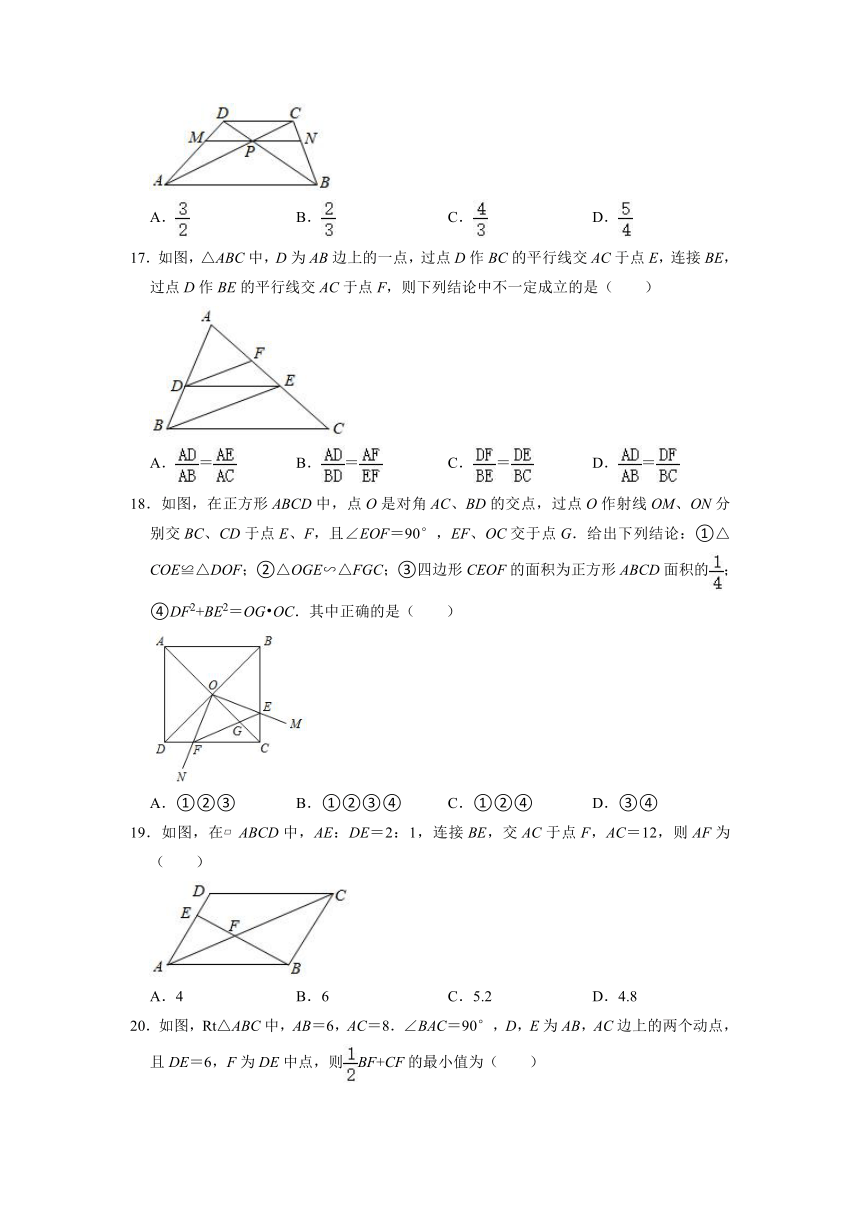
17.如图,△ABC中,D为AB边上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论中不一定成立的是( )
A.=
B.=
C.=
D.=
18.如图,在正方形ABCD中,点O是对角AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,EF、OC交于点G.给出下列结论:①△COE≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG?OC.其中正确的是( )
A.①②③
B.①②③④
C.①②④
D.③④
19.如图,在?ABCD中,AE:DE=2:1,连接BE,交AC于点F,AC=12,则AF为( )
A.4
B.6
C.5.2
D.4.8
20.如图,Rt△ABC中,AB=6,AC=8.∠BAC=90°,D,E为AB,AC边上的两个动点,且DE=6,F为DE中点,则BF+CF的最小值为( )
A.2
B.
C.
D.
21.如图,已知Rt△ABC中,AC=BC=2,∠ACB=90°,将△ABC绕点A沿逆时针方向旋转后得到△ADE,直线BD、CE相交于点F,连接AF.则下列结论中:
①△ABD∽△ACE;②∠BFC=45°;③F为BD的中点;④△AFC面积的最大值为.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
22.如图,在矩形ABCD中,AB=6,BC=3,E是对角线BD上一动点,过E作MN⊥BD于E,交AB于M,交CD于N,当点E在BD上移动时,MN的长是( )
A.3
B.
C.
D.无法确定
23.如图,在四边形ABCD中,∠ADB=∠ACB=90°,∠DAB=55°,∠ABC=65°.则的值为( )
A.
B.
C.
D.
24.如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①;②△AFC∽△AGD;③2AE2=AH?AC;④DG⊥AC.其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
25.如图,在平面直角坐标系中,平行四边形OABC的顶点O与原点重合,点A在x轴的正半轴上,AC⊥OC.按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OC于点E,F;②分别以点E、F为圆心,大于EF的长为半径作弧,两弧在∠AOC内交于点P;③作射线OP,交边AC于点D.若CD=3,AD=5,则点B的坐标为( )
A.(10,)
B.(,)
C.(12,)
D.(,)
26.如图,在△ABC中,点D在BC边上,连接AD,DE∥AC交AB于点E,过点E作EF∥BC交AD于点F,下列式子一定正确的是( )
A.=
B.=
C.=
D.=
27.如图,在平行四边形ABCD中,点E是AD上一点,AE=2ED,连接BE交AC于点G,延长BE交CD的延长线于点F,则的值为( )
A.
B.
C.
D.
28.如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则的值为( )
A.
B.
C.
D.
29.如图,在△ABC中,BC=3,点D为AC延长线上的一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,若∠CBD=∠A,则AB的长为( )
A.6
B.5
C.4
D.4.2
二.解答题
30.如图,在菱形ABCD中,点E,F分别在边BC,DC上,AE与BD交于点H,AE的延长线与DC的延长线交于点G,∠BAE=∠DAF.
(1)求证:AD2=DF?DG;
(2)若HE=4,EG=5,求AH的长.
31.如图,已知在△ABC中,BC>AB,BD平分∠ABC,交边AC于点D,E是BC边上一点,且BE=BA,过点A作AG∥DE,分别交BD、BC于点F、G,联结FE.
(1)求证:四边形AFED是菱形;
(2)求证:AB2=BG?BC.
32.如图,正方形ABCD与正方形AEFG有公共的顶点A,连接DG,BE,AC,CF.
(1)求证:DG=BE;
(2)求的值.
33.在平行四边形ABCD中,AB=3,BC=4.
(1)如图1,∠A=90°,N为BC上一点,M为AB上一点,若DN⊥MN,CN<BN,BM=1,求证:DN=MN;
(2)如图2,N为BC上一点,M为AB上一点,若∠DNM=∠B=60°,求证:.
34.如图,△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边在BC上,顶点G,H分别在AC,AB上,已知BC=30cm,AD=20cm.
(1)求证:△AHG∽△ABC;
(2)求正方形EFGH的面积.
35.在锐角△ABC中,点D,E分别在AC、AB上,AG⊥BC与点G,AF⊥DE于F,∠EAF=∠GAC.
(1)求证:△AEF∽△ACG.
(2)求证:∠ADE=∠B.
(3)若AD=3,AB=5,求.
参考答案
1.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴△EDF∽△CBF,
∴,
∵点E是边AD的中点,
∴AD=2ED,
∴BC=2ED,
∴=,
故选:B.
2.解:∵GE∥BD,GF∥AC,
∴=,,
∴.
故选:C.
3.解:∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∴S△ADE:S△ABC=,
即,
故,
故选:A.
4.解:∵∠C=90°,AB=10,BC=8.
∴AC===6,
∵EF∥AB,
∴∠ABD=∠BDF,又∠ABD=∠FBD,
∴∠FBD=∠BDF,
∴FB=FD,
∴EF=2FB,
∵EF∥AB,
∴△CEF∽△CAB,
∴==,
∴==,
解得,BF=,
∴AE=.
故选:B.
5.解:∵==,
∴DE:BC=1:3,故A错误;
∵=,
∴=,∠A=∠A,
∴△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,故B和C错误;
∵=,
∴=,∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
故选:D.
6.解:∵BD=2AD,AD+BD=AB,
∴=,
∵DE∥BC,
∴△ADE∽ABC,
∴==,
∵DE∥BC,
∴△ODE∽OCB,
∴==,
∴=()2=,=,
∵S△ODE=1,
∴S△OCB=9,S△OCE=3,
∴S△BCE=S△OCB+S△OCE=12,
故选:D.
7.解:∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,CD=AB=3,BC=AD=2,
∴DE===,
∵AF⊥DE,
∴∠AFD=∠C=90°,
∴∠DAF+∠ADF=∠ADF+∠CDE=90°,
∴∠DAF=∠CDE,
∴△ADF∽△DCE,
∴=,
∴=,
∴AF=.
故选:A.
8.解:由作图可知:PQ垂直平分AB,AB=DB,
∴AC=BC,∠BDA=∠A,
∵∠A=30°,
∴∠ABC=∠A=30°,∠BDA=30°,
∵∠BCD=∠A+∠ABC,
∴∠BCD=30°+30°=60°,故A选项不符合题意;
∵∠A=∠A,∠ABC=∠BDA=30°,
∴△ABC∽△ADB,
∴AB:AD=AC:AB,
即AB2=AD?AC,故B选项不符合题意;
∵∠A+∠BDA+∠ABD=180°,
∴∠ABD=180°﹣30°﹣30°=120°,
∵∠CAB=30°,
∴∠ABD=4∠CAB,故C选项不符合题意;
过B作BE⊥AD,垂足为点E,
∵∠A=30°,
∴AB=2BE,
∴AE=,
∵AB=DB,
∴AD=2AE=AB,故D选项符合题意,
故选:D.
9.解:如图,连接GF,
∵AD=BE,DG∥AC,EF∥BC,
∴===,
∵∠DHE=∠GHF,
∴△DHE∽△GHF,
∴=()2,
∵S2=18,S3=6,
∴=,S△HGF=S3,
∴S△DHE=()2×3=27,
则S4的值为27.
故选:C.
10.解:∵∠DAB=∠B=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∵AD⊥CD,CD=1,
∴AD=,AC=2,
延长AD、BC交于点G,如图,
∵∠DAB=∠B=60°,
∴∠G=60°,
∴△ABG为等边三角形,
∵AC平分∠DAB,
∴C为GB的中点,且AC⊥GB,
∴AB=AC÷cos30°=,
连接EC,
∵E为AB边的中点,
∴EC=AB=,
∵C为GB的中点,
∴EC∥AD,
∴△EFC∽△DFA,
∴==,
∴AF=AC=.
故选:D.
11.解:∵∠AED=∠C,∠EAD=∠CAB,
∴△AED∽△ACB,
∴,即AE?AB=AD?AC,
∵AB=8,AD?AC=26,
∴AE=,
故选:C.
12.解:如图,取DE中点O,连接AO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB=180°﹣∠ABC=105°,
∵AF⊥BC,
∴AF⊥AD,
∴∠DAE=90°,
∴OA=DE=OD=OE,
∵DE=2AB,
∴OA=AB,
∴∠AOB=∠ABO,∠ADO=∠DAO,∠AED=∠EAO,
∵∠AOB=∠ADO+∠DAO=2∠ADO,
∴∠ABD=∠AOB=2∠ADO,
∴∠ABD+∠ADO+∠DAB=180°,
∴∠ADO=25°,∠AOB=50°,
∴∠AED+∠EAO+∠AOD=180°,
∴∠AED=65°.
故选:B.
13.解:∵矩形AFRK的面积为3,矩形KRGB的面积为6,
∴正方形ABGF的面积为9,
∴AB=AF=BG=3,
∵矩形AFRK的面积为3,矩形KRGB的面积为6,
∴AK=1,BK=2,
∵PQ⊥CR,CR⊥FG,FG∥AB,
∴CR⊥AB,PQ∥AB,
∵∠ACB=∠CBQ=90°,
∴AC∥BQ,
∴四边形ABQC是平行四边形,
∴CQ=AB=3,
∵∠CAB=∠CAK,∠ACB=∠AKC,
∴△ACK∽△ABC,
∴,
∴AC2=1×3,
∴AC==DC,
∴CK===,
∵∠DCA=∠PCK=90°,
∴∠DCP=∠ACK,
又∵∠D=∠AKC=90°,
∴△DCP∽△KCA,
∴,
∴,
∴PC=,
∴PQ=PC+CQ=3+,
故选:C.
14.解:∵PE∥AB,
∴△DEF∽△DAB,
∴=,
∵PF∥CD,
∴△BPF∽△BDC,
∴=,
∴+=+=1,所以A选项符合题意,D选项不符合题意;
∵PE∥AB,
∴=,
∵PF∥CD,
∴=,
∴=,所以B选项不符合题意;
∵PE∥AB,
∴=,
∵=,
∴=,所以C选项不符合题意.
故选:A.
15.解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,故①正确;
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在Rt△ABH和Rt△DCF中,
,
∴Rt△ABH≌Rt△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,故②正确;
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故④正确;
∵∠FDE=45°,∠DFE=∠FAE+∠AEF=22.5°+45°=67.5°,
∴∠DEF=180°﹣45°﹣67.5°=67.5°,
∴DF=DE,故③正确;
如图,连接HE,
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故⑤错误,
∴正确的是①②③④,
故选:C.
16.解:设PM=x,PN=y,
∵AB∥CD,MN∥AB,
∴AB∥MN∥CD,
∴△CDP∽△ABP,
∵AB=2,△PDC与△PAB的面积比为1:4,
∴CD=1,
∵AB∥MN∥CD,
∴△DMP∽△DAB,△CPN∽△CAB,
∴,,
∵,
∴,
∴,
解得:x=y=,
∴MN=x+y=.
故选:C.
17.解:∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠C,
∵∠A=∠A,
∴△ADE∽△ABC,
∴,故A成立;
∵DF∥BE,
∴,故B成立;
∵DE∥BC,DF∥BE,
∴,,
∴,故C成立;
∵DF∥BC,
∴,而BE≠BC,故D不成立.
故选:D.
18.解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE=∠EOF﹣∠COF=90°﹣∠COF,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
故①正确;
②由①全等可得OE=OF,
∴∠OEF=∠OCF=45°,∠OGE=∠CGF,
∴△OGE∽△FGC,
故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的,
故③正确;
④∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,
在Rt△ECF中,CE2+CF2=EF2,
∴DF2+BE2=EF2,
∵∠OCE=∠OEG=45°,∠EOG=∠COE,
∴△EOG∽△COE,
∴,
∴OG?OC=EO2≠EF2,
∴DF2+BE2≠OG?OC,
故④不正确;
综上所述,正确的是①②③,
故选:A.
19.解:在?ABCD中,AD=BC,AD∥BC,
∵AE:DE=2:1,
∴AE=AD,
∴AE=AD=BC
∵AD∥BC,
∴∠AEF=∠CBF,∠FAE=∠FCB,
∴△AFE∽△CFB,
∴=,
∵AC=12,
∴AF=×12=4.8.
故选:D.
20.解:连接AF,在AB上截取AG=1.5,连接FG,CG,
∵∠BAC=90°,F为DE中点,
∴AF=DE=3,
∵=,∠GAF=∠BAF,
∴△AGF∽△AFB,
∴,
∴GF=BF,
∴BF+CF=GF+CF,
∴当点G,点F,点C共线时,最小值为GC的长,
∵CG===,
∴BF+CF的最小值为,
故选:D.
21.解:由旋转性质可知,AC=BC=AE=DE=2,AB=AD=,
∴.
∵∠DAE=∠CAB=45°,
∴∠DAE+∠EAB=∠CAB+∠EAB,即∠DAB=∠EAC.
故△ABD∽△ACE,故①正确;
设AB、CE交于点G,如图.
由△ABD∽△ACE,可得∠DBA=∠ECA,
又∠FGB=∠CGA,
∴∠BFC=∠BAC=45°,
故②正确;
由∠BFC=∠BAC=45°,可知A、C、B、F四点共圆,
由圆内接四边形性质知∠BFA+∠BCA=180°,
则∠BFA=90°,
又AB=AD,△ABD为等腰三角形,
∴由三线合一性质知AF为BD上中线,即F为BD中点.
故③正确;
以AC作△AFC底边,则F到AC距离为高,设高为h,
当h最大时,△AFC面积才最大.
此时h=,
故△AFC的面积最大值为,
故④错误.
故正确的一共有3个,
故选:C.
22.解:如图,过点M作MH⊥DC于H,
∴∠MHC=∠C=∠ABC=90°,
∴四边形BCHM是矩形,
∴MH=BC=3,
∵AB=CD=6,BC=AD=3,
∴BD===3,
∵MN⊥BD,
∴∠DEN=∠MHN=∠C=90°,
∴∠MNH+∠BDC=∠BDC+∠DBC=90°,
∴∠DBC=∠MNH,
∴△DBC∽△MNH,
∴,
∴=,
∴MN=,
故选:C.
23.解:
∵∠ADB=∠ACB=90°,∠DAB=55°,∠ABC=65°,
∴∠DBA=35°,∠CAB=25°,∠DAC=55°﹣25°=30°.
设AC,BD的交点为O,∠DOA=∠COB,
∴Rt△ADO∽Rt△BCO,
∴∠CBO=∠DAO=30°.
∵直角三角形中30°角所对直角边是斜边的一半,
∴OD=OA,OC=OB,
∴OD:OA=OC:OB=1:2,
∵∠DOC=∠AOB,
∴△DOC∽△AOB,
∴==,
故选:B.
24.解:①∵四边形AEFG和四边形ABCD均为正方形,
∴∠EAG=∠BAD=90°,
又∵∠EAB=90°﹣∠BAG,∠GAD=90°﹣∠BAG,
∴∠EAB=∠GAD,
∴选项①正确;
②∵四边形AEFG和四边形ABCD均为正方形,
∴AD=DC,AG=FG,
∴AC=AD,AF=AG,
∴=,=,即=,
又∵∠DAG+∠GAC=∠FAC+∠GAC,
∴∠DAG=∠CAF,
∴△AFC∽△AGD,
∴选项②正确;
③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线,
∴∠AFH=∠ACF=45°,
又∵∠FAH=∠CAF,
∴△HAF∽△FAC,
∴=,即AF2=AC?AH,
又∵AF=AE,
∴2AE2=AH?AC,
∴选项③正确;
④由②知△AFC∽△AGD,
又∵四边形ABCD为正方形,AC为对角线,
∴∠ADG=∠ACF=45°,
∴DG在正方形另外一条对角线上,
∴DG⊥AC,
∴④正确,
故选:D.
25.解:过D作DQ⊥OA交OA于点Q,过B作BH⊥OA于H,如图所示,
由题意知:OD是∠COA的角平分线,
∴∠COD=∠QOD,
∵AC⊥OC,DQ⊥OA,
在△COD和△QOD中,
∴△COD≌QOD)(AAS),
∴DC=DQ=3,
∴OC=OQ,
∵AD=5,
∴AQ===4,
设OC=OQ=a,
在Rt△AOC中,有a2+(3+5)2=(a+4)2,
解得:a=6,
∴OA=OQ+QA=6+4=10,
∵四边形OACB是平行四边形,
∴OC∥AB,
∴∠COA=∠BAH,OC=AB,
∴△ABH∽△OAC,
∴,,
∴AH===,
BH==,
∴OH=OA+AH=10+=,
∴B(,).
故选:D.
26.解:∵EF∥BC,
∴≠,
故A错误;
∵EF∥BC,EF∥BC,
∴,,
∴,
故B错误;
∵EF∥BC,EF∥BC,
∴,,
∴,
故C正确;
∵EF∥BC,EF∥BC,
∴,
故D错误;
故选:C.
27.解:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△ABG∽△CFG,
∴=
∵△ABE∽△DFE,
∴=,
∵AE=2ED,
∴AB=2DF,
∴=,
∴=.
故选:A.
28.解:∵四边形AEDC是正方形,
∴∠EAC=∠DCA=90°,EA∥DC,
∴∠MAB=∠CBA,
又∵四边形AFGB是正方形,
∴AB=BG,∠ABG=90°,
∴∠ACB=∠ABM=90°,
∴△ACB∽△MBA,
∴,
又∵M是BG中点,设BM=a,
∴AB=BG=2a,AM=a,
∴AC===,BC=,
∴IA=,
又AE∥DC,IM与BC相交于O,
∴,,
∴CO=AM=,
∴BO=BC﹣OC=﹣=,
∴.
故选:A.
29.解:∵DH∥AB,
∴△ABC∽△DHC,
∴,
∵BC=3,AC=3CD,
∴CH=1.
∴BH=4,
∵∠CBD=∠A,∠ABC=∠BHD,
∴△ABC∽△BHD,
∴,
∵△ABC∽△DHC,
∴,
∴AB=3DH,
∴,
解得DH=2,
∴AB=3DH=3×2=6,
故选:A.
30.(1)证明:∵四边形ABCD为菱形,
∴AB∥DG,
∴∠BAE=∠DGA,
又∠BAE=∠DAF,
∴∠DGA=∠DAF,
又∠ADF=∠GDA,
∴△ADF∽△GDA,
∴,
∴AD2=DF?DG.
(2)解:∵AB∥GD,
∴,
∵AD∥BC,
∴,
∴,
即AH2=HG?HE=(4+5)×4=36,
∴AH=6.
31.解:(1)证明:
∵BD平分∠ABC,
∴∠ABF=∠EBF.
∵BA=BE,BF=BF,
∴△ABF≌△EBF(SAS).
∴AF=EF.
同理可得△ABD≌△EBD(SAS).
∴AD=ED,∠ADB=∠EDB.
∵AG∥DE,
∴∠AFD=∠EDF.
∴∠AFD=∠ADF.
∴AF=AD.
∴AF=FE=ED=DA.
∴四边形AFED是菱形.
(2)证明:由(1)得△ABF≌△EBF,
∴∠BAG=∠BEF.
∵四边形AFED是菱形,
∴AD∥FE.
∴∠BEF=∠C.
∴∠BAG=∠C.
∵∠ABG=∠CBA,
∴△ABG∽△CBA.
∴,
即AB2=BG?BC.
32.证明:(1)∵四边形ABCD和四边形AEFG是正方形,
∴AD=AB,AG=AE,∠DAB=∠GAE=90°,
∴∠DAB﹣∠GAB=∠GAE﹣∠GAB,
∴∠DAG=∠BAE.
∴△DAG≌△BAE.
∴DG=BE.
(2)解:如图,连接AF.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠BAC=45°,
AC=.
∴,
同理,.
∴=.
∵∠CAF=∠CAB﹣∠FAB=45°﹣∠FAB,
同理可得∠BAE=45°﹣∠FAB,
∴∠CAF=∠BAE.
∴△CAF∽△BAE.
∴.
33.证明:(1)根据题意可知AB=CD=3,BC=AD=4,∠B=∠C=∠A=90°,
不妨设CN=x,则BN=4﹣x,
∵DN⊥MN,
∴∠MNB+∠DNC=90°,
又∠DNC+∠NDC=90°,
∴∠MNB=∠NDC,
∴△BMN∽△CND,
∴,即,
解得x=1或x=3,
∵CN<BN,
∴x=1,
∴CN=BM=1,BN=DC=3,DN==,MN==,
∴DN=MN;
(2)如下图,
过点D作DE=DN,并与BC的延长线交于点E,
则∠E=∠DNE,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC=60°,
∵AD∥BC,
∴∠ADC=∠DCE=60°,∠ADN=∠DNE,
∴∠B=DCE=∠DNM=60°,
∵∠BMN+∠MNB=120°,∠MNB+∠DNE=120°,
∴∠BMN=∠DNE,
∴∠BMN=∠E,
∴△BMN∽△CED,
∴
∴.
34.(1)证明:∵四边形EFGH为正方形,
∴GH∥EF.
∴GH∥BC,
∴△AHG∽△ABC.
解:(2)设AD与HG的交点为M,如图,
则AM是△AHG的高.
由(1)知:△AHG∽△ABC.
∴.
∵四边形EFGH为正方形,
∴HG=HE=FG,HG∥BC.
∵AD⊥BC,
∴MD=FG.
∴HG=MD.
设HG=MD=xcm,则AM=AD﹣MD=(20﹣x)cm,
∴.
解得:x=12,
∴正方形EFGH的边长为12cm.
∴正方形EFGH的面积为:12×12=144cm2
35.证明:(1)∵AG⊥BC,AF⊥DE于,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC
∴△AEF∽△ACG.
(2)由(1)知△AEF∽△ACG,
∴∠AEF=∠C
∵∠DAE=∠BAC(公共角),
∴△EAD∽△CAB.
∴∠ADE=∠B.
解:(3)由(2)知:△ADE∽△ABC,
∴.
由(1)知△AEF∽△ACG,
∴.
∴.
∵AD=3,AB=5,
∴.
同步能力提高训练(附答案)
一.选择题
1.如图,在平行四边形ABCD中,点E是边AD上的中点,EC交对角线BD于点F,则等于( )
A.
B.
C.
D.
2.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.
B.
C.
D.
3.如图,在△ABC中,DE∥BC,=2,记△ADE的面积为a,四边形DBCE的面积为b,则的值是( )
A.
B.
C.
D.
4.如图,在△ABC中,∠C=90°,AB=10,BC=8.E是AC边上一动点,过点E作EF∥AB交BC于点F,D为线段EF的中点,当BD平分∠ABC时,AE的长度是( )
A.
B.
C.
D.
5.如图△ABC中,点D、E分别在AB、AC上,且==,下列结论正确的是( )
A.DE:BC=1:2
B.△ADE与△ABC的面积比为1:3
C.△ADE与△ABC的周长比为1:2
D.DE∥BC
6.如图,D、E分别为△ABC的边AB、AC上的点,且DE∥BC,CD、BE相交于点O,BD=2AD.若△ODE的面积为1,则△BCE的面积为( )
A.6
B.8
C.10
D.12
7.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,则点A到直线DE的距离AF的长度为( )
A.
B.
C.2.5
D.
8.已知∠MAN=30°,点B在射线AM上,按以下步骤作图:
①分别以A,B为圆心,大于AB的长为半径画弧,两弧相交于P,Q两点;
②作直线PQ,交射线AN于点C,连接BC;
③以B为圆心,BA长为半径画弧,交射线AN于点D.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠BCD=60°
B.AB2=AD?AC
C.∠ABD=4∠CBA
D.AD=2AB
9.《几何原本》有一个图形:在△ABC中,D,E是边AB上的两点(AD<AE),且满足AD=BE.过点D,E分别作BC的平行线,过点D作AC的平行线,它们将△ABC分成如图的5个部分,其面积依次记为S1,S2,S3,S4,S5.若S2=18,S3=6,则S4的值为( )
A.9
B.18
C.27
D.54
10.如图,在四边形ABCD中,∠DAB=∠B=60°,AD⊥CD,AC平分∠DAB,E为AB边的中点,连接DE交AC于F.若CD=1,则线段AF的长度为( )
A.
B.
C.1
D.
11.如图,在△ABC中,AB=8,D,E分别是边AC和AB上的点,且∠AED=∠C,若AD?AC=26,则AE的长为( )
A.
B.3
C.
D.4
12.平行四边形ABCD中,∠ABC=75度,AF⊥BC,AF交BD于E,DE=2AB,则∠AED=( )度.
A.60
B.65
C.70
D.75
13.如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,交线段AB于点K,再过点C作PQ⊥CR分别交边DE,BH于点P、Q.若矩形AFRK的面积为3,矩形KRGB的面积为6,则PQ的长为( )
A.4.5
B.5
C.3
D.3
14.如图,四边形ABCD中,P为对角线BD上一点,过点P作PE∥AB,交AD于点E,过点P作PF∥CD,交BC于点F,则下列所给的结论中,不一定正确的是( )
A.
B.
C.
D.
15.如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:①BH垂直平分AE;②AH=DF;③DF=DE;④∠AEF=45°;⑤S四边形EFHG=S△DEF+S△AGH,其中正确的结论有( )个.
A.2
B.3
C.4
D.5
16.在四边形ABCD中AB∥CD,对角线AC与BD交于P,过点P作AB的平行线,交AD、BC于M、N.若AB=2,△PDC与△PAB的面积比为1:4,则MN的长是( )
A.
B.
C.
D.
17.如图,△ABC中,D为AB边上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论中不一定成立的是( )
A.=
B.=
C.=
D.=
18.如图,在正方形ABCD中,点O是对角AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,EF、OC交于点G.给出下列结论:①△COE≌△DOF;②△OGE∽△FGC;③四边形CEOF的面积为正方形ABCD面积的;④DF2+BE2=OG?OC.其中正确的是( )
A.①②③
B.①②③④
C.①②④
D.③④
19.如图,在?ABCD中,AE:DE=2:1,连接BE,交AC于点F,AC=12,则AF为( )
A.4
B.6
C.5.2
D.4.8
20.如图,Rt△ABC中,AB=6,AC=8.∠BAC=90°,D,E为AB,AC边上的两个动点,且DE=6,F为DE中点,则BF+CF的最小值为( )
A.2
B.
C.
D.
21.如图,已知Rt△ABC中,AC=BC=2,∠ACB=90°,将△ABC绕点A沿逆时针方向旋转后得到△ADE,直线BD、CE相交于点F,连接AF.则下列结论中:
①△ABD∽△ACE;②∠BFC=45°;③F为BD的中点;④△AFC面积的最大值为.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
22.如图,在矩形ABCD中,AB=6,BC=3,E是对角线BD上一动点,过E作MN⊥BD于E,交AB于M,交CD于N,当点E在BD上移动时,MN的长是( )
A.3
B.
C.
D.无法确定
23.如图,在四边形ABCD中,∠ADB=∠ACB=90°,∠DAB=55°,∠ABC=65°.则的值为( )
A.
B.
C.
D.
24.如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①;②△AFC∽△AGD;③2AE2=AH?AC;④DG⊥AC.其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
25.如图,在平面直角坐标系中,平行四边形OABC的顶点O与原点重合,点A在x轴的正半轴上,AC⊥OC.按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OC于点E,F;②分别以点E、F为圆心,大于EF的长为半径作弧,两弧在∠AOC内交于点P;③作射线OP,交边AC于点D.若CD=3,AD=5,则点B的坐标为( )
A.(10,)
B.(,)
C.(12,)
D.(,)
26.如图,在△ABC中,点D在BC边上,连接AD,DE∥AC交AB于点E,过点E作EF∥BC交AD于点F,下列式子一定正确的是( )
A.=
B.=
C.=
D.=
27.如图,在平行四边形ABCD中,点E是AD上一点,AE=2ED,连接BE交AC于点G,延长BE交CD的延长线于点F,则的值为( )
A.
B.
C.
D.
28.如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则的值为( )
A.
B.
C.
D.
29.如图,在△ABC中,BC=3,点D为AC延长线上的一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,若∠CBD=∠A,则AB的长为( )
A.6
B.5
C.4
D.4.2
二.解答题
30.如图,在菱形ABCD中,点E,F分别在边BC,DC上,AE与BD交于点H,AE的延长线与DC的延长线交于点G,∠BAE=∠DAF.
(1)求证:AD2=DF?DG;
(2)若HE=4,EG=5,求AH的长.
31.如图,已知在△ABC中,BC>AB,BD平分∠ABC,交边AC于点D,E是BC边上一点,且BE=BA,过点A作AG∥DE,分别交BD、BC于点F、G,联结FE.
(1)求证:四边形AFED是菱形;
(2)求证:AB2=BG?BC.
32.如图,正方形ABCD与正方形AEFG有公共的顶点A,连接DG,BE,AC,CF.
(1)求证:DG=BE;
(2)求的值.
33.在平行四边形ABCD中,AB=3,BC=4.
(1)如图1,∠A=90°,N为BC上一点,M为AB上一点,若DN⊥MN,CN<BN,BM=1,求证:DN=MN;
(2)如图2,N为BC上一点,M为AB上一点,若∠DNM=∠B=60°,求证:.
34.如图,△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边在BC上,顶点G,H分别在AC,AB上,已知BC=30cm,AD=20cm.
(1)求证:△AHG∽△ABC;
(2)求正方形EFGH的面积.
35.在锐角△ABC中,点D,E分别在AC、AB上,AG⊥BC与点G,AF⊥DE于F,∠EAF=∠GAC.
(1)求证:△AEF∽△ACG.
(2)求证:∠ADE=∠B.
(3)若AD=3,AB=5,求.
参考答案
1.解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴△EDF∽△CBF,
∴,
∵点E是边AD的中点,
∴AD=2ED,
∴BC=2ED,
∴=,
故选:B.
2.解:∵GE∥BD,GF∥AC,
∴=,,
∴.
故选:C.
3.解:∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∴S△ADE:S△ABC=,
即,
故,
故选:A.
4.解:∵∠C=90°,AB=10,BC=8.
∴AC===6,
∵EF∥AB,
∴∠ABD=∠BDF,又∠ABD=∠FBD,
∴∠FBD=∠BDF,
∴FB=FD,
∴EF=2FB,
∵EF∥AB,
∴△CEF∽△CAB,
∴==,
∴==,
解得,BF=,
∴AE=.
故选:B.
5.解:∵==,
∴DE:BC=1:3,故A错误;
∵=,
∴=,∠A=∠A,
∴△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,故B和C错误;
∵=,
∴=,∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
故选:D.
6.解:∵BD=2AD,AD+BD=AB,
∴=,
∵DE∥BC,
∴△ADE∽ABC,
∴==,
∵DE∥BC,
∴△ODE∽OCB,
∴==,
∴=()2=,=,
∵S△ODE=1,
∴S△OCB=9,S△OCE=3,
∴S△BCE=S△OCB+S△OCE=12,
故选:D.
7.解:∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,CD=AB=3,BC=AD=2,
∴DE===,
∵AF⊥DE,
∴∠AFD=∠C=90°,
∴∠DAF+∠ADF=∠ADF+∠CDE=90°,
∴∠DAF=∠CDE,
∴△ADF∽△DCE,
∴=,
∴=,
∴AF=.
故选:A.
8.解:由作图可知:PQ垂直平分AB,AB=DB,
∴AC=BC,∠BDA=∠A,
∵∠A=30°,
∴∠ABC=∠A=30°,∠BDA=30°,
∵∠BCD=∠A+∠ABC,
∴∠BCD=30°+30°=60°,故A选项不符合题意;
∵∠A=∠A,∠ABC=∠BDA=30°,
∴△ABC∽△ADB,
∴AB:AD=AC:AB,
即AB2=AD?AC,故B选项不符合题意;
∵∠A+∠BDA+∠ABD=180°,
∴∠ABD=180°﹣30°﹣30°=120°,
∵∠CAB=30°,
∴∠ABD=4∠CAB,故C选项不符合题意;
过B作BE⊥AD,垂足为点E,
∵∠A=30°,
∴AB=2BE,
∴AE=,
∵AB=DB,
∴AD=2AE=AB,故D选项符合题意,
故选:D.
9.解:如图,连接GF,
∵AD=BE,DG∥AC,EF∥BC,
∴===,
∵∠DHE=∠GHF,
∴△DHE∽△GHF,
∴=()2,
∵S2=18,S3=6,
∴=,S△HGF=S3,
∴S△DHE=()2×3=27,
则S4的值为27.
故选:C.
10.解:∵∠DAB=∠B=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∵AD⊥CD,CD=1,
∴AD=,AC=2,
延长AD、BC交于点G,如图,
∵∠DAB=∠B=60°,
∴∠G=60°,
∴△ABG为等边三角形,
∵AC平分∠DAB,
∴C为GB的中点,且AC⊥GB,
∴AB=AC÷cos30°=,
连接EC,
∵E为AB边的中点,
∴EC=AB=,
∵C为GB的中点,
∴EC∥AD,
∴△EFC∽△DFA,
∴==,
∴AF=AC=.
故选:D.
11.解:∵∠AED=∠C,∠EAD=∠CAB,
∴△AED∽△ACB,
∴,即AE?AB=AD?AC,
∵AB=8,AD?AC=26,
∴AE=,
故选:C.
12.解:如图,取DE中点O,连接AO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB=180°﹣∠ABC=105°,
∵AF⊥BC,
∴AF⊥AD,
∴∠DAE=90°,
∴OA=DE=OD=OE,
∵DE=2AB,
∴OA=AB,
∴∠AOB=∠ABO,∠ADO=∠DAO,∠AED=∠EAO,
∵∠AOB=∠ADO+∠DAO=2∠ADO,
∴∠ABD=∠AOB=2∠ADO,
∴∠ABD+∠ADO+∠DAB=180°,
∴∠ADO=25°,∠AOB=50°,
∴∠AED+∠EAO+∠AOD=180°,
∴∠AED=65°.
故选:B.
13.解:∵矩形AFRK的面积为3,矩形KRGB的面积为6,
∴正方形ABGF的面积为9,
∴AB=AF=BG=3,
∵矩形AFRK的面积为3,矩形KRGB的面积为6,
∴AK=1,BK=2,
∵PQ⊥CR,CR⊥FG,FG∥AB,
∴CR⊥AB,PQ∥AB,
∵∠ACB=∠CBQ=90°,
∴AC∥BQ,
∴四边形ABQC是平行四边形,
∴CQ=AB=3,
∵∠CAB=∠CAK,∠ACB=∠AKC,
∴△ACK∽△ABC,
∴,
∴AC2=1×3,
∴AC==DC,
∴CK===,
∵∠DCA=∠PCK=90°,
∴∠DCP=∠ACK,
又∵∠D=∠AKC=90°,
∴△DCP∽△KCA,
∴,
∴,
∴PC=,
∴PQ=PC+CQ=3+,
故选:C.
14.解:∵PE∥AB,
∴△DEF∽△DAB,
∴=,
∵PF∥CD,
∴△BPF∽△BDC,
∴=,
∴+=+=1,所以A选项符合题意,D选项不符合题意;
∵PE∥AB,
∴=,
∵PF∥CD,
∴=,
∴=,所以B选项不符合题意;
∵PE∥AB,
∴=,
∵=,
∴=,所以C选项不符合题意.
故选:A.
15.解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,故①正确;
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在Rt△ABH和Rt△DCF中,
,
∴Rt△ABH≌Rt△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,故②正确;
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故④正确;
∵∠FDE=45°,∠DFE=∠FAE+∠AEF=22.5°+45°=67.5°,
∴∠DEF=180°﹣45°﹣67.5°=67.5°,
∴DF=DE,故③正确;
如图,连接HE,
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故⑤错误,
∴正确的是①②③④,
故选:C.
16.解:设PM=x,PN=y,
∵AB∥CD,MN∥AB,
∴AB∥MN∥CD,
∴△CDP∽△ABP,
∵AB=2,△PDC与△PAB的面积比为1:4,
∴CD=1,
∵AB∥MN∥CD,
∴△DMP∽△DAB,△CPN∽△CAB,
∴,,
∵,
∴,
∴,
解得:x=y=,
∴MN=x+y=.
故选:C.
17.解:∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠C,
∵∠A=∠A,
∴△ADE∽△ABC,
∴,故A成立;
∵DF∥BE,
∴,故B成立;
∵DE∥BC,DF∥BE,
∴,,
∴,故C成立;
∵DF∥BC,
∴,而BE≠BC,故D不成立.
故选:D.
18.解:①在正方形ABCD中,OC=OD,∠COD=90°,∠ODC=∠OCB=45°,
∵∠EOF=90°,
∴∠COE=∠EOF﹣∠COF=90°﹣∠COF,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
故①正确;
②由①全等可得OE=OF,
∴∠OEF=∠OCF=45°,∠OGE=∠CGF,
∴△OGE∽△FGC,
故②正确;
③由①全等可得四边形CEOF的面积与△OCD面积相等,
∴四边形CEOF的面积为正方形ABCD面积的,
故③正确;
④∵△COE≌△DOF,
∴CE=DF,
∵四边形ABCD为正方形,
∴BC=CD,
∴BE=CF,
在Rt△ECF中,CE2+CF2=EF2,
∴DF2+BE2=EF2,
∵∠OCE=∠OEG=45°,∠EOG=∠COE,
∴△EOG∽△COE,
∴,
∴OG?OC=EO2≠EF2,
∴DF2+BE2≠OG?OC,
故④不正确;
综上所述,正确的是①②③,
故选:A.
19.解:在?ABCD中,AD=BC,AD∥BC,
∵AE:DE=2:1,
∴AE=AD,
∴AE=AD=BC
∵AD∥BC,
∴∠AEF=∠CBF,∠FAE=∠FCB,
∴△AFE∽△CFB,
∴=,
∵AC=12,
∴AF=×12=4.8.
故选:D.
20.解:连接AF,在AB上截取AG=1.5,连接FG,CG,
∵∠BAC=90°,F为DE中点,
∴AF=DE=3,
∵=,∠GAF=∠BAF,
∴△AGF∽△AFB,
∴,
∴GF=BF,
∴BF+CF=GF+CF,
∴当点G,点F,点C共线时,最小值为GC的长,
∵CG===,
∴BF+CF的最小值为,
故选:D.
21.解:由旋转性质可知,AC=BC=AE=DE=2,AB=AD=,
∴.
∵∠DAE=∠CAB=45°,
∴∠DAE+∠EAB=∠CAB+∠EAB,即∠DAB=∠EAC.
故△ABD∽△ACE,故①正确;
设AB、CE交于点G,如图.
由△ABD∽△ACE,可得∠DBA=∠ECA,
又∠FGB=∠CGA,
∴∠BFC=∠BAC=45°,
故②正确;
由∠BFC=∠BAC=45°,可知A、C、B、F四点共圆,
由圆内接四边形性质知∠BFA+∠BCA=180°,
则∠BFA=90°,
又AB=AD,△ABD为等腰三角形,
∴由三线合一性质知AF为BD上中线,即F为BD中点.
故③正确;
以AC作△AFC底边,则F到AC距离为高,设高为h,
当h最大时,△AFC面积才最大.
此时h=,
故△AFC的面积最大值为,
故④错误.
故正确的一共有3个,
故选:C.
22.解:如图,过点M作MH⊥DC于H,
∴∠MHC=∠C=∠ABC=90°,
∴四边形BCHM是矩形,
∴MH=BC=3,
∵AB=CD=6,BC=AD=3,
∴BD===3,
∵MN⊥BD,
∴∠DEN=∠MHN=∠C=90°,
∴∠MNH+∠BDC=∠BDC+∠DBC=90°,
∴∠DBC=∠MNH,
∴△DBC∽△MNH,
∴,
∴=,
∴MN=,
故选:C.
23.解:
∵∠ADB=∠ACB=90°,∠DAB=55°,∠ABC=65°,
∴∠DBA=35°,∠CAB=25°,∠DAC=55°﹣25°=30°.
设AC,BD的交点为O,∠DOA=∠COB,
∴Rt△ADO∽Rt△BCO,
∴∠CBO=∠DAO=30°.
∵直角三角形中30°角所对直角边是斜边的一半,
∴OD=OA,OC=OB,
∴OD:OA=OC:OB=1:2,
∵∠DOC=∠AOB,
∴△DOC∽△AOB,
∴==,
故选:B.
24.解:①∵四边形AEFG和四边形ABCD均为正方形,
∴∠EAG=∠BAD=90°,
又∵∠EAB=90°﹣∠BAG,∠GAD=90°﹣∠BAG,
∴∠EAB=∠GAD,
∴选项①正确;
②∵四边形AEFG和四边形ABCD均为正方形,
∴AD=DC,AG=FG,
∴AC=AD,AF=AG,
∴=,=,即=,
又∵∠DAG+∠GAC=∠FAC+∠GAC,
∴∠DAG=∠CAF,
∴△AFC∽△AGD,
∴选项②正确;
③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线,
∴∠AFH=∠ACF=45°,
又∵∠FAH=∠CAF,
∴△HAF∽△FAC,
∴=,即AF2=AC?AH,
又∵AF=AE,
∴2AE2=AH?AC,
∴选项③正确;
④由②知△AFC∽△AGD,
又∵四边形ABCD为正方形,AC为对角线,
∴∠ADG=∠ACF=45°,
∴DG在正方形另外一条对角线上,
∴DG⊥AC,
∴④正确,
故选:D.
25.解:过D作DQ⊥OA交OA于点Q,过B作BH⊥OA于H,如图所示,
由题意知:OD是∠COA的角平分线,
∴∠COD=∠QOD,
∵AC⊥OC,DQ⊥OA,
在△COD和△QOD中,
∴△COD≌QOD)(AAS),
∴DC=DQ=3,
∴OC=OQ,
∵AD=5,
∴AQ===4,
设OC=OQ=a,
在Rt△AOC中,有a2+(3+5)2=(a+4)2,
解得:a=6,
∴OA=OQ+QA=6+4=10,
∵四边形OACB是平行四边形,
∴OC∥AB,
∴∠COA=∠BAH,OC=AB,
∴△ABH∽△OAC,
∴,,
∴AH===,
BH==,
∴OH=OA+AH=10+=,
∴B(,).
故选:D.
26.解:∵EF∥BC,
∴≠,
故A错误;
∵EF∥BC,EF∥BC,
∴,,
∴,
故B错误;
∵EF∥BC,EF∥BC,
∴,,
∴,
故C正确;
∵EF∥BC,EF∥BC,
∴,
故D错误;
故选:C.
27.解:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴△ABG∽△CFG,
∴=
∵△ABE∽△DFE,
∴=,
∵AE=2ED,
∴AB=2DF,
∴=,
∴=.
故选:A.
28.解:∵四边形AEDC是正方形,
∴∠EAC=∠DCA=90°,EA∥DC,
∴∠MAB=∠CBA,
又∵四边形AFGB是正方形,
∴AB=BG,∠ABG=90°,
∴∠ACB=∠ABM=90°,
∴△ACB∽△MBA,
∴,
又∵M是BG中点,设BM=a,
∴AB=BG=2a,AM=a,
∴AC===,BC=,
∴IA=,
又AE∥DC,IM与BC相交于O,
∴,,
∴CO=AM=,
∴BO=BC﹣OC=﹣=,
∴.
故选:A.
29.解:∵DH∥AB,
∴△ABC∽△DHC,
∴,
∵BC=3,AC=3CD,
∴CH=1.
∴BH=4,
∵∠CBD=∠A,∠ABC=∠BHD,
∴△ABC∽△BHD,
∴,
∵△ABC∽△DHC,
∴,
∴AB=3DH,
∴,
解得DH=2,
∴AB=3DH=3×2=6,
故选:A.
30.(1)证明:∵四边形ABCD为菱形,
∴AB∥DG,
∴∠BAE=∠DGA,
又∠BAE=∠DAF,
∴∠DGA=∠DAF,
又∠ADF=∠GDA,
∴△ADF∽△GDA,
∴,
∴AD2=DF?DG.
(2)解:∵AB∥GD,
∴,
∵AD∥BC,
∴,
∴,
即AH2=HG?HE=(4+5)×4=36,
∴AH=6.
31.解:(1)证明:
∵BD平分∠ABC,
∴∠ABF=∠EBF.
∵BA=BE,BF=BF,
∴△ABF≌△EBF(SAS).
∴AF=EF.
同理可得△ABD≌△EBD(SAS).
∴AD=ED,∠ADB=∠EDB.
∵AG∥DE,
∴∠AFD=∠EDF.
∴∠AFD=∠ADF.
∴AF=AD.
∴AF=FE=ED=DA.
∴四边形AFED是菱形.
(2)证明:由(1)得△ABF≌△EBF,
∴∠BAG=∠BEF.
∵四边形AFED是菱形,
∴AD∥FE.
∴∠BEF=∠C.
∴∠BAG=∠C.
∵∠ABG=∠CBA,
∴△ABG∽△CBA.
∴,
即AB2=BG?BC.
32.证明:(1)∵四边形ABCD和四边形AEFG是正方形,
∴AD=AB,AG=AE,∠DAB=∠GAE=90°,
∴∠DAB﹣∠GAB=∠GAE﹣∠GAB,
∴∠DAG=∠BAE.
∴△DAG≌△BAE.
∴DG=BE.
(2)解:如图,连接AF.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠BAC=45°,
AC=.
∴,
同理,.
∴=.
∵∠CAF=∠CAB﹣∠FAB=45°﹣∠FAB,
同理可得∠BAE=45°﹣∠FAB,
∴∠CAF=∠BAE.
∴△CAF∽△BAE.
∴.
33.证明:(1)根据题意可知AB=CD=3,BC=AD=4,∠B=∠C=∠A=90°,
不妨设CN=x,则BN=4﹣x,
∵DN⊥MN,
∴∠MNB+∠DNC=90°,
又∠DNC+∠NDC=90°,
∴∠MNB=∠NDC,
∴△BMN∽△CND,
∴,即,
解得x=1或x=3,
∵CN<BN,
∴x=1,
∴CN=BM=1,BN=DC=3,DN==,MN==,
∴DN=MN;
(2)如下图,
过点D作DE=DN,并与BC的延长线交于点E,
则∠E=∠DNE,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC=60°,
∵AD∥BC,
∴∠ADC=∠DCE=60°,∠ADN=∠DNE,
∴∠B=DCE=∠DNM=60°,
∵∠BMN+∠MNB=120°,∠MNB+∠DNE=120°,
∴∠BMN=∠DNE,
∴∠BMN=∠E,
∴△BMN∽△CED,
∴
∴.
34.(1)证明:∵四边形EFGH为正方形,
∴GH∥EF.
∴GH∥BC,
∴△AHG∽△ABC.
解:(2)设AD与HG的交点为M,如图,
则AM是△AHG的高.
由(1)知:△AHG∽△ABC.
∴.
∵四边形EFGH为正方形,
∴HG=HE=FG,HG∥BC.
∵AD⊥BC,
∴MD=FG.
∴HG=MD.
设HG=MD=xcm,则AM=AD﹣MD=(20﹣x)cm,
∴.
解得:x=12,
∴正方形EFGH的边长为12cm.
∴正方形EFGH的面积为:12×12=144cm2
35.证明:(1)∵AG⊥BC,AF⊥DE于,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC
∴△AEF∽△ACG.
(2)由(1)知△AEF∽△ACG,
∴∠AEF=∠C
∵∠DAE=∠BAC(公共角),
∴△EAD∽△CAB.
∴∠ADE=∠B.
解:(3)由(2)知:△ADE∽△ABC,
∴.
由(1)知△AEF∽△ACG,
∴.
∴.
∵AD=3,AB=5,
∴.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
