2021—2022学年冀教版九年级数学上册28.3圆心角的概念和性质 同步练习题(word含答案)
文档属性
| 名称 | 2021—2022学年冀教版九年级数学上册28.3圆心角的概念和性质 同步练习题(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览


文档简介
28.3 第1课时 圆心角的概念和性质
【基础练习】
知识点
1 圆心角的定义及求法
1.下列四个图中的角,是圆心角的是( )
图1
2.如图2,AB为☉O的弦,∠OAB=60°,则弦AB所对的圆心角的度数为 .?
图2
如图3,在△ABC中,∠ACB=90°,∠B=35°,以点C为圆心,AC长为半径的圆交AB于点D,则所对的圆心角等于 °.?
图3
知识点
2 圆心角、弧、弦的关系
4.如图4,AB,CD是☉O的两条弦.依据圆心角、弧、弦的关系将下面横线上的内容补充完整.
图4
(1)∵∠AOB=∠COD,∴= ,AB= ;?
(2)∵,∴∠AOB= ,AB= ;?
(3)∵AB=CD,∴ =, =∠COD.?
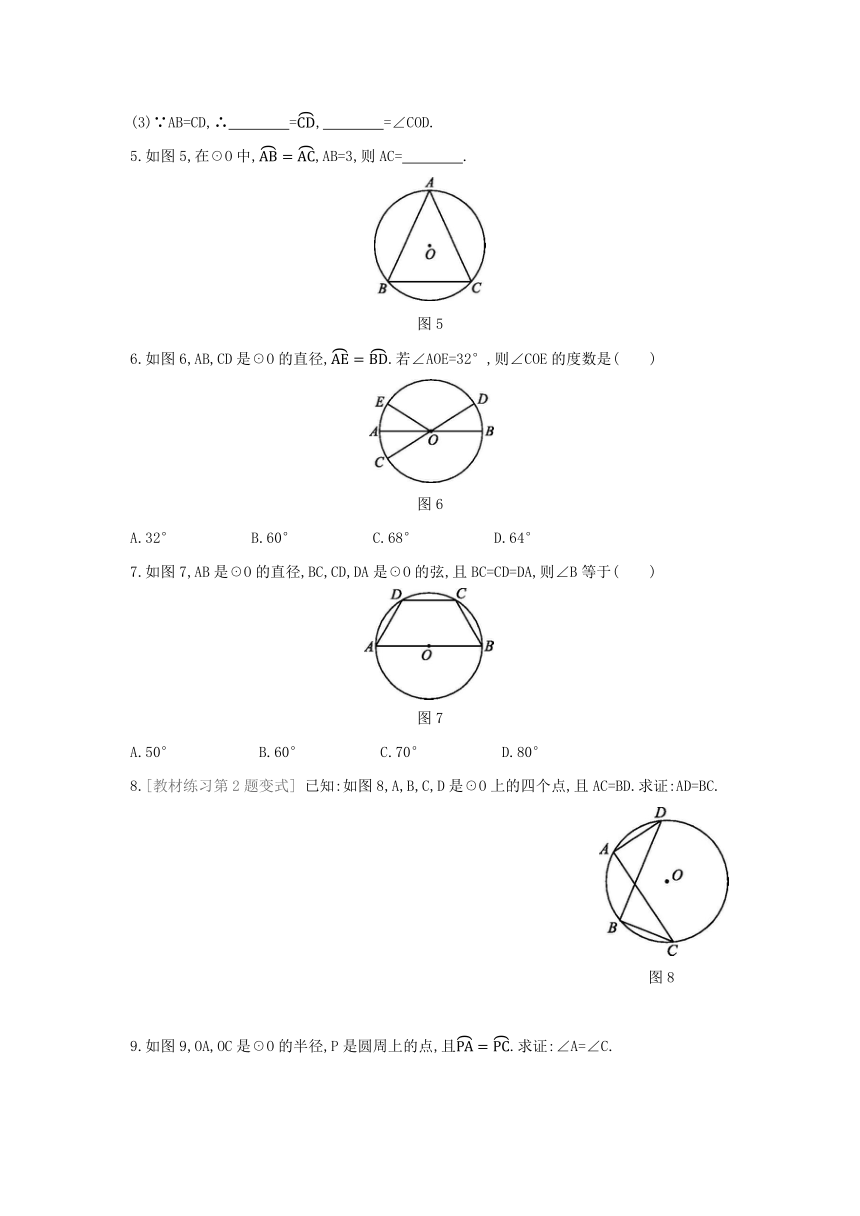
5.如图5,在☉O中,,AB=3,则AC= .?
图5
6.如图6,AB,CD是☉O的直径,.若∠AOE=32°,则∠COE的度数是( )
图6
A.32°
B.60°
C.68°
D.64°
7.如图7,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则∠B等于( )
图7
A.50°
B.60°
C.70°
D.80°
8.[教材练习第2题变式]
已知:如图8,A,B,C,D是☉O上的四个点,且AC=BD.求证:AD=BC.
图8
9.如图9,OA,OC是☉O的半径,P是圆周上的点,且.求证:∠A=∠C.
图9
【能力提升】
10.如图10,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么所对的圆心角的度数是( )
图10
A.60°
B.75°
C.80°
D.90°
11.下列说法正确的是
( )
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的弧相等
12.在☉O中,=2,则AB 2CD(填“>”“<”或“=”).?
13.如图11,AB和DE是☉O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
图11
14.如图12,M为☉O上一点,,MD⊥OA于点D,ME⊥OB于点E.求证:MD=ME.
图12
15.如图13,在☉O中,,∠ACB=60°.
(1)求证:∠AOB=∠BOC=∠AOC;
(2)若D是的中点,求证:四边形OADB是菱形.
图13
16.如图14,在☉O中,∠AON=60°,B是的中点,P是直径MN上的一个动点,☉O的半径为1,求AP+BP的最小值.
图14
答案
1.D 2.60° 3.70
4.(1) CD (2)∠COD CD
(3) ∠AOB
5.3 [解析]∵在☉O中,,∴AC=AB=3.
6.D [解析]∵,∴∠BOD=∠AOE=32°.∵∠BOD=∠AOC,∴∠AOC=32°,
∴∠COE=32°+32°=64°.
7.B
8.证明:∵AC=BD,
∴,
∴--,
∴,∴BC=AD.
9.证明:如图,连接OP.∵,∴PA=PC.
在△POA与△POC中,
∴△POA≌△POC(SSS),
∴∠A=∠C.
10.D [解析]如图,作AB的垂直平分线,作BC的垂直平分线,它们的交点Q为这条圆弧所在圆的圆心.连接AQ,CQ,易知∠AQC=90°,即所对的圆心角的度数是90°.
11.B
12.< [解析]如图,取的中点E,连接AE,BE.
则,
∴AE=BE=CD.
在△ABE中,AE+BE>AB,即2CD>AB,
∴AB<2CD.
13.3 [解析]如图,连接OC.∵AC∥DE,
∴∠A=∠1,∠2=∠ACO.
∵OA=OC,∴∠A=∠ACO,
∴∠1=∠2,
∴CE=BE=3.
14.证明:如图所示,连接MO.
∵,
∴∠MOD=∠MOE.
∵MD⊥OA,ME⊥OB,
∴∠MDO=∠MEO=90°.又∵OM=OM,
∴△MDO≌△MEO,∴MD=ME.
15.证明:(1)∵,∴AB=AC.
又∵∠ACB=60°,∴△ABC是等边三角形,
∴AB=BC=AC,
∴∠AOB=∠BOC=∠AOC.
(2)由(1)易知∠AOB=120°.如图,连接OD.
∵D是的中点,
∴,
∴∠AOD=∠BOD=∠AOB=60°.
又∵OD=OA,OD=OB,
∴△OAD和△OBD都是等边三角形,
则OA=AD=OD,OB=BD=OD,
∴OA=AD=BD=OB,
∴四边形OADB是菱形.
16.[解析]根据圆是轴对称图形,在下半圆上作点B关于MN的对称点B',连接AB'交MN于点P,易得BP=B'P,∠AOB'=90°,再根据“两点之间线段最短”可求.
解:作点B关于MN的对称点B',则点B'在☉O上,连接AB'交MN于点P,连接BP,根据“两点之间线段最短”,可知此时AP+BP的值最小,连接OB,OB'.
由对称性可知BP=B'P,,
∴AP+BP=AP+B'P=AB',∠BON=∠B'ON.
∵∠AON=60°,B是的中点,
∴∠BON=∠AON=30°,
∴∠B'ON=30°,∴∠AOB'=90°.
在Rt△AOB'中,∵OA=OB'=1,
∴AB'=,∴AP+BP=.
故AP+BP的最小值是.
【基础练习】
知识点
1 圆心角的定义及求法
1.下列四个图中的角,是圆心角的是( )
图1
2.如图2,AB为☉O的弦,∠OAB=60°,则弦AB所对的圆心角的度数为 .?
图2
如图3,在△ABC中,∠ACB=90°,∠B=35°,以点C为圆心,AC长为半径的圆交AB于点D,则所对的圆心角等于 °.?
图3
知识点
2 圆心角、弧、弦的关系
4.如图4,AB,CD是☉O的两条弦.依据圆心角、弧、弦的关系将下面横线上的内容补充完整.
图4
(1)∵∠AOB=∠COD,∴= ,AB= ;?
(2)∵,∴∠AOB= ,AB= ;?
(3)∵AB=CD,∴ =, =∠COD.?
5.如图5,在☉O中,,AB=3,则AC= .?
图5
6.如图6,AB,CD是☉O的直径,.若∠AOE=32°,则∠COE的度数是( )
图6
A.32°
B.60°
C.68°
D.64°
7.如图7,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则∠B等于( )
图7
A.50°
B.60°
C.70°
D.80°
8.[教材练习第2题变式]
已知:如图8,A,B,C,D是☉O上的四个点,且AC=BD.求证:AD=BC.
图8
9.如图9,OA,OC是☉O的半径,P是圆周上的点,且.求证:∠A=∠C.
图9
【能力提升】
10.如图10,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么所对的圆心角的度数是( )
图10
A.60°
B.75°
C.80°
D.90°
11.下列说法正确的是
( )
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的弧相等
12.在☉O中,=2,则AB 2CD(填“>”“<”或“=”).?
13.如图11,AB和DE是☉O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
图11
14.如图12,M为☉O上一点,,MD⊥OA于点D,ME⊥OB于点E.求证:MD=ME.
图12
15.如图13,在☉O中,,∠ACB=60°.
(1)求证:∠AOB=∠BOC=∠AOC;
(2)若D是的中点,求证:四边形OADB是菱形.
图13
16.如图14,在☉O中,∠AON=60°,B是的中点,P是直径MN上的一个动点,☉O的半径为1,求AP+BP的最小值.
图14
答案
1.D 2.60° 3.70
4.(1) CD (2)∠COD CD
(3) ∠AOB
5.3 [解析]∵在☉O中,,∴AC=AB=3.
6.D [解析]∵,∴∠BOD=∠AOE=32°.∵∠BOD=∠AOC,∴∠AOC=32°,
∴∠COE=32°+32°=64°.
7.B
8.证明:∵AC=BD,
∴,
∴--,
∴,∴BC=AD.
9.证明:如图,连接OP.∵,∴PA=PC.
在△POA与△POC中,
∴△POA≌△POC(SSS),
∴∠A=∠C.
10.D [解析]如图,作AB的垂直平分线,作BC的垂直平分线,它们的交点Q为这条圆弧所在圆的圆心.连接AQ,CQ,易知∠AQC=90°,即所对的圆心角的度数是90°.
11.B
12.< [解析]如图,取的中点E,连接AE,BE.
则,
∴AE=BE=CD.
在△ABE中,AE+BE>AB,即2CD>AB,
∴AB<2CD.
13.3 [解析]如图,连接OC.∵AC∥DE,
∴∠A=∠1,∠2=∠ACO.
∵OA=OC,∴∠A=∠ACO,
∴∠1=∠2,
∴CE=BE=3.
14.证明:如图所示,连接MO.
∵,
∴∠MOD=∠MOE.
∵MD⊥OA,ME⊥OB,
∴∠MDO=∠MEO=90°.又∵OM=OM,
∴△MDO≌△MEO,∴MD=ME.
15.证明:(1)∵,∴AB=AC.
又∵∠ACB=60°,∴△ABC是等边三角形,
∴AB=BC=AC,
∴∠AOB=∠BOC=∠AOC.
(2)由(1)易知∠AOB=120°.如图,连接OD.
∵D是的中点,
∴,
∴∠AOD=∠BOD=∠AOB=60°.
又∵OD=OA,OD=OB,
∴△OAD和△OBD都是等边三角形,
则OA=AD=OD,OB=BD=OD,
∴OA=AD=BD=OB,
∴四边形OADB是菱形.
16.[解析]根据圆是轴对称图形,在下半圆上作点B关于MN的对称点B',连接AB'交MN于点P,易得BP=B'P,∠AOB'=90°,再根据“两点之间线段最短”可求.
解:作点B关于MN的对称点B',则点B'在☉O上,连接AB'交MN于点P,连接BP,根据“两点之间线段最短”,可知此时AP+BP的值最小,连接OB,OB'.
由对称性可知BP=B'P,,
∴AP+BP=AP+B'P=AB',∠BON=∠B'ON.
∵∠AON=60°,B是的中点,
∴∠BON=∠AON=30°,
∴∠B'ON=30°,∴∠AOB'=90°.
在Rt△AOB'中,∵OA=OB'=1,
∴AB'=,∴AP+BP=.
故AP+BP的最小值是.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
