2021-2022学年冀教版九年级数学上册25.6相似三角形的应用同步辅优训练(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册25.6相似三角形的应用同步辅优训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 852.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《25.6相似三角形的应用》
同步优生辅导训练(附答案)
1.小亮想用镜子测量一棵松树的高度,如图所示,第一次他把镜子水平放置在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子水平放置在D点,人在G点正好看到树尖A,已知B、C、F、D、H在水平地面的同一直线上,小亮的眼睛距离地面1.7m,得CD=34m,CF=1.7m,DH=3.4m,请你求出松树的高.
2.在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,某数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度,在同一时刻的阳光下,他们合作完成了以下工作:
(1)测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如图1).
(2)测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米,
(1)在横线上直接填写甲树的高度为
米,
(2)图3为图2的示意图,请利用图3求出乙树的高度.
3.如图,建筑物BC上有一根旗杆AB,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上,已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A、B、C在一条直线上,点C、D、E、G在一条直线上,AC、FD均垂直于CG,请你帮助小芳求出这座建筑物的高BC.
4.新型冠状病毒感染引发“疫情就是命令,现场就是战场”.家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进0.8m到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
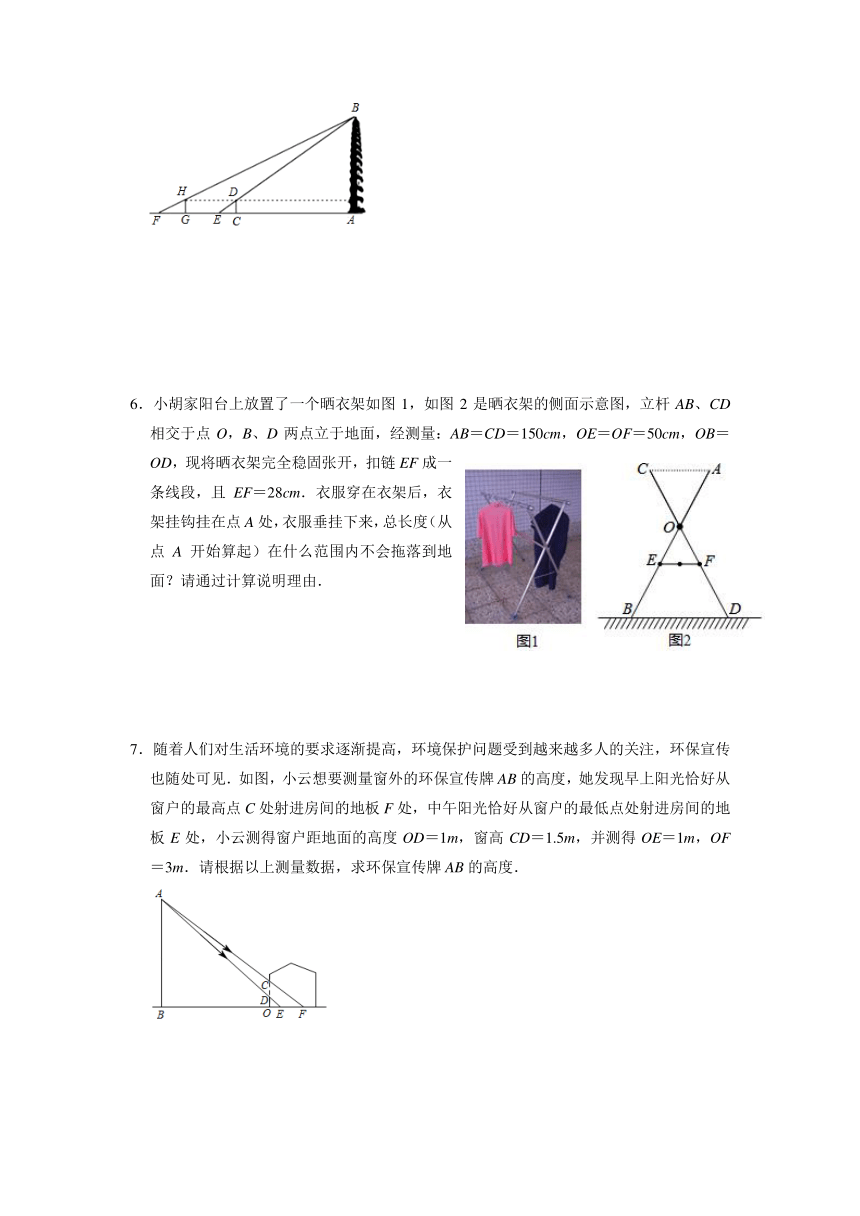
5.西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.
6.小胡家阳台上放置了一个晒衣架如图1,如图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面,经测量:AB=CD=150cm,OE=OF=50cm,OB=OD,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=28cm.衣服穿在衣架后,衣架挂钩挂在点A处,衣服垂挂下来,总长度(从点A开始算起)在什么范围内不会拖落到地面?请通过计算说明理由.
7.随着人们对生活环境的要求逐渐提高,环境保护问题受到越来越多人的关注,环保宣传也随处可见.如图,小云想要测量窗外的环保宣传牌AB的高度,她发现早上阳光恰好从窗户的最高点C处射进房间的地板F处,中午阳光恰好从窗户的最低点处射进房间的地板E处,小云测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求环保宣传牌AB的高度.
8.如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
9.如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合:小亮又在点C1处直立高3m的竹竿CD1,然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m,EC1=6m,C1E1=3m,求电线杆AB的高度.
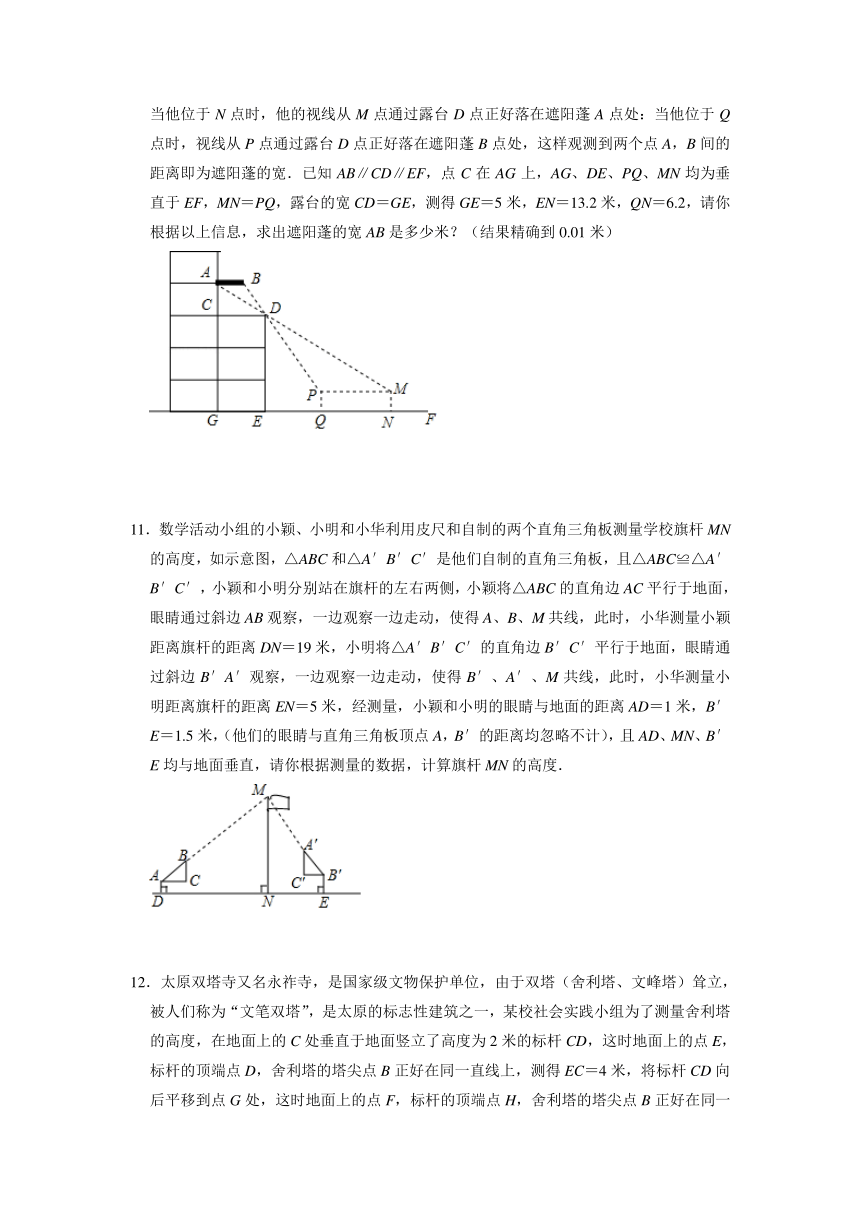
10.周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳蓬的宽度,如图,由于无法直接测量,小凯便在楼前面的地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳蓬A点处:当他位于Q点时,视线从P点通过露台D点正好落在遮阳蓬B点处,这样观测到两个点A,B间的距离即为遮阳蓬的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、PQ、MN均为垂直于EF,MN=PQ,露台的宽CD=GE,测得GE=5米,EN=13.2米,QN=6.2,请你根据以上信息,求出遮阳蓬的宽AB是多少米?(结果精确到0.01米)
11.数学活动小组的小颖、小明和小华利用皮尺和自制的两个直角三角板测量学校旗杆MN的高度,如示意图,△ABC和△A′B′C′是他们自制的直角三角板,且△ABC≌△A′B′C′,小颖和小明分别站在旗杆的左右两侧,小颖将△ABC的直角边AC平行于地面,眼睛通过斜边AB观察,一边观察一边走动,使得A、B、M共线,此时,小华测量小颖距离旗杆的距离DN=19米,小明将△A′B′C′的直角边B′C′平行于地面,眼睛通过斜边B′A′观察,一边观察一边走动,使得B′、A′、M共线,此时,小华测量小明距离旗杆的距离EN=5米,经测量,小颖和小明的眼睛与地面的距离AD=1米,B′E=1.5米,(他们的眼睛与直角三角板顶点A,B′的距离均忽略不计),且AD、MN、B′E均与地面垂直,请你根据测量的数据,计算旗杆MN的高度.
12.太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
13.某学校的学生为了对小雁塔有基本的认识,在老师的带领下对小雁塔进行了测量.测量方法如下:如图,间接测得小雁塔底部点D到地面上一点E的距离为115.2米,小雁塔的顶端为点B,且BD⊥DE,在点E处竖直放一个木棒,其顶端为C,CE=1.72米,在DE的延长线上找一点A,使A、C、B三点在同一直线上,测得AE=4.8米.求小雁塔的高度.
14.我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
求:(1)装饰画与墙壁的夹角∠CAD的度数(精确到1°);
(2)装饰画顶部到墙壁的距离DC(精确到0.01米).
15.如图所示,小明在地面上放置一个平面镜C,选择合适的位置,刚好在平面镜C中看到旗杆DE的顶部,此时小明与平面镜C的水平距离BC为2m,旗杆底部与平面镜的水平距离CE为16m.若小明的眼睛与地面的距离AB为1.6m,试求旗杆DE的高度.
16.20世纪90年代以来,我国户外广告行业取得了突飞猛进的发展,户外广告装置多设立于城市道路、铁路、公路等主要交通干道边上,面向密集的车流和人流.某天,小芳走到如图所示的C处时,看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住,3s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是21.6km/h,假设AB∥PQ,公路宽为10m,求小芳所在C处到公路南侧PQ的距离.
17.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
18.为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
19.《铁血红安》在中央一台热播后,吸引了众多游客前往影视基地游玩.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高1.7米.请根据以上数据求出城楼的高度.
20.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.
21.如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.(=1.732,=1.414,=2.449,精确到1米).
22.小明想用镜子测量一棵松树的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子放在D点,人在G点正好看到树尖A.已知小明的眼睛距离地面1.70m,量得CD=12m,CF=1.8m,DH=3.8m.请你求出松树的高.
23.在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
24.雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
25.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
26.刘徽(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是
;
(2)在(1)中提到刘徽的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
27.如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
28.如图1是一个某物体的支架实物图,图2是其右侧部分抽象后的几何图形,其中点C是支杆PD上一可转动点,点P是中间竖杆BA上的一动点,当点P沿BA滑动时,点D随之在地面上滑动,点A是动点P能到达的最顶端位置,当P运动到点A时,PC与BC重合于竖杆BA,经测量PC=BC=50cm,CD=60cm,设AP=xcm,竖杆BA的最下端B到地面的距离BO=ycm.
(1)求AB的长;
(2)当∠PCB=90°时,求y的值;(参考数据:1.414,结果精确到0.1cm)
(3)当点P运动时,试求出y与x的函数关系式.
29.图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米.
(1)求AP长的取值范围;
(2)当∠CPN=60°时,求AP的值;
(3)在阳光垂直照射下,伞张得最开时,求伞下的阴影(假定为圆面)面积S(结果保留π).
参考答案
1.解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH,
∵AB⊥BC,EF⊥BC,GH⊥BC,
∴△BAC∽△FEC、△ADB∽△GDH,
设AB=x,BC=y,
∴,
解得.
答;这棵松树的高为34米.
2.解:(1)设甲树的高度为x米,
根据题意得:=,
解得:x=5.1(米),
故答案为:5.1;
(2)连接AE并延长交BC的延长线于M,延长ED交AB于F,连接AD,如图3所示:
∵CD=0.3m,DE=0.2m,
BC=4.4m,
∴EF=4.4+0.2=4.6(m),
∴=,
∴=,
∴AF=(m),
∴AB=AF+BF=+0.3=6.05(m).
答:乙树的高度为6.05米.
3.解:由题意可得,∠ACE=∠EDF=90°,∠AEC=∠FED,
∴△ACE∽△FDE,
∴,
即,
∴CD=,
由题意可得,∠BCG=∠FDG=90°,∠BGC=∠FGD,
∴△BCG∽△FDG,
∴,
即,
∴6.5BC=4(CD+6.5),
∴6.5BC=4×,
∴BC=14(米),
∴这座建筑物的高BC为14米.
4.解:延长ED交AB于H,延长MQ交BA的延长线于T.
由题意MT=2m,MQ=0.8m,
∴QT=MT﹣MQ=2﹣0.8=1.2(m),
∵四边形BCDH是矩形,
∴DH=BC=300(m),
∵QT∥DH,
∴===,
∵MT∥DE,
∴=,
∴=,
∴EH=500(m),
∴DE=500﹣300=200(m)
5.解:∵△EDC∽△EBA,△FHG∽△FBA,
∴=,=,
∵DC=HG,
∴=,
∴=,
∴CA=106(米),
∵=,
∴=,
∴AB=55(米),
答:大雁塔的高度AB为55米.
6.解:∵AB、CD相交于点O,
∴∠AOC=∠BOD
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠BOD),
同理可证:∠OBD=∠ODB=(180°﹣∠BOD),
∴∠OAC=∠OBD,
∴AC∥BD,
在Rt△OEM中,OM===48(cm),
过点A作AH⊥BD于点H,
同理可证:EF∥BD,
∴∠ABH=∠OEM,则Rt△OEM∽Rt△ABH,
∴=,
∴AH===144(cm),
所以垂挂在衣架上的连衣裙总长度小于144cm时,连衣裙才不会拖落到地面上.
7.解:∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=xm,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴=,
=,
解得:x=10.
经检验:x=10是原方程的解.
答:AB的高度是10m.
8.解:(1)如图1,
∵PM∥BD,
∴△APM∽△ABD,
=,即=,
∴AP=AB,
∵NQ∥AC,
∴△BNQ∽△BCA,
∴=,即=,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴=,即=,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
9.解:∵DC⊥AED1C1⊥AEBA⊥AE
∴DC∥D1C1∥BA,
∴△F1D1N∽△F1BG.
∴.
∵DC∥BA,
∴△FDM∽△FBG.
∴.
∵D1N=DM,
∴,
即.
∴GM=16m.
∵,
∴.
∴BG=13.5m.
∴AB=BG+GA=15(m).
答:电线杆AB的高度为15m.
10.解:延长MP交DE于H,如图,
则HM=EN=13.2米,CD=GE=5米,
MP=NQ=6.2米,
∵CD∥HM,
∴∠ADC=∠DMH,
∴Rt△ACD∽Rt△DHM,
∴==,
∵AB∥MP,
∴△ABD∽△MPD,
∴==,
即=,
解得AB=2.35(米).
答:遮阳篷的宽AB是2.35米.
11.解:过点C作CE'⊥MN于E',过点C′作C′F⊥MN于F,
则E'F=B′E﹣AD=1.5﹣1=0.5(m),AE'=DN=19,B′F=EN=5,
∵△ABC≌△A′B′C′,
∴∠MAE'=∠B′MF,
∵∠AE'M=∠B′FM=90°,
∴△AME'∽△MB'F,
∴,
∴=
∴MF=,
∴MN=MF+FN=11,
答:旗杆MN的高度约为11米.
12.解:∵△EDC∽△EBA,△FHG∽△FBA,
∴=,=,∵DC=HG,
∴=,
∴=,
∴CA=106(米),
∵=,
∴=,
∴AB=55(米),
答:舍利塔的高度AB为55米.
13.解:由题意可得:△AEC∽△ADB,
则=,
故=,
解得:DB=43,
答:小雁塔的高度为43m.
14.解:(1)∵AD=0.66米,
∴AE=AD=0.33米,
在Rt△ABE中,
∵sin∠ABE==,
∴∠ABE≈12°,
∵∠CAD+∠DAB=90°,∠ABE+∠DAB=90°,
∴∠CAD=∠ABE=12°.
∴镜框与墙壁的夹角∠CAD的度数约为12°.
(2)解法一:
在Rt△ACD中,
∵sin∠CAD=,
∴CD=AD?sin∠CAD=0.66×sin12°≈0.14米,
解法二:
∵∠CAD=∠ABE,
∠ACD=∠AEB=90°,
∴△ACD∽△BEA,
∴,
∴,
∴CD≈0.14米.
∴镜框顶部到墙壁的距离CD约是0.14米.
15.解:由题意得∠ACB=∠DCE,
∵∠ABC=∠DEC,
∴△ACB∽△DCE,
∴,
即.
∴DE=12.8
答:旗杆的高度为12.8m.
16.解:设小芳所在C处到公路南侧PQ的距离为xm,
21.6km/h=21.6×=6m/s,
∵AB∥PQ,
∴△CAB∽△CPQ,
∴,
∴=,
∴x=30,
∴小芳所在C处到公路南侧PQ的距离为30m.
17.解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米.
18.解:如图所示:过点E作EB⊥AC于点B,
由题意可得:DC=BE=4.6m,DE=BC=2.5m,
∵同一时刻身高1.5米小刚站立时在太阳光下的影长恰好为1米,
∴==,
解得:AB=6.9,
故AC=AB+BC=6.9+2.5=9.4(m),
答:新安装的照明路灯的灯杆的高度为9.4m.
19.解:过点A作AM⊥EF于点M,交CD于点N,
由题意可得:AN=2m,CN=2﹣1.65=0.35(m),MN=40m,
∵CN∥EM,
∴△ACN∽△AEM,
∴=,
∴=,
解得:EM=7.35,
∵AB=MF=1.65m,
故城楼的高度为:7.35+1.65﹣1.7=7.3(米),
答:城楼的高度为7.3m.
20.解:作DE⊥AB于点E,
根据题意得:=,
=,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
21.解:延长AD交BC于E点,则∠AEB=30°,
作DQ⊥BC于Q,
在Rt△DCQ中,∠DCQ=45°,DC=8,
∴DQ=QC=8sin45°=8×=4,
在Rt△DQE中,QE=≈9.8(米)
∴BE=BC+CQ+QE≈35.5(米)
在Rt△ABE中,AB=BEtan30°≈20(米)
答:旗杆的高度约为20米.
22.解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH,
∵AB⊥BC,EF⊥BC,GH⊥BC,
∴△BAC∽△FEC、△ADB∽△GDH,
设AB=x,BC=y
∴,
解得.
答;这棵古松的高约为10.2米
23.解:这种测量方法可行.
理由如下:
设旗杆高AB=x.过F作FG⊥AB于G,交CE于H(如图).
所以△AGF∽△EHF.
因为FD=1.5,GF=27+3=30,HF=3,
所以EH=3.5﹣1.5=2,AG=x﹣1.5.
由△AGF∽△EHF,
得=,
即=,
所以x﹣1.5=20,
解得x=21.5(米)
答:旗杆的高为21.5米.
24.解:由题意知,CD=EF=1.6m,DG=2.8m,DF=1.5m,GH=1.7m,
∴FH=2.8﹣1.5+1.7=3m,
∵AB⊥BH,CD⊥BH,EF⊥BH,
∴△CDG∽△ABG,△EFH∽△ABH,
∴=,=,
∴=,即=,
解得BD=21,
∴,
解得AB=13.6.
即该校旗杆的高度AB为13.6m.
25.解:∵AB⊥BH,CD⊥BH,EF⊥BH,
∴AB∥CD∥EF,
∴△CDG∽△ABG,△EFH∽△ABH,
∴=,=,
∵CD=DG=EF=2m,DF=52m,FH=4m,
∴=,
=,
∴=,
解得BD=52,
∴=,
解得AB=54.
答:建筑物的高为54米.
26.解:(1)《海岛算经》;
(2)由题意,得,AH⊥HG,CB⊥HG,
∴∠AHF=90°,∠CBF=90°,
∴∠AHF=∠CBF,
∵∠AFB=∠CFB,
∴△CBF∽△AHF,
∴=,
同理可得=,
∵BF=123,BD=1000,DG=127,
∴HF=HB+123,HG=HB+1000+127=HB+1127,
∴=,=,
解得HB=30750,HA=753,
答:AH为753丈,HB为30750步.
27.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴=,
∴=,
解得:CH=3.78米,
∴DC=CH+DH=3.78+1.5=5.28米.
答:故树高DC为5.28米.
28.解:(1)∵当P运动到点A时,PC与BC重合于竖杆BA,
∴由题意可得:AB=PC+BC=50+50=100(cm);
(2)如图,过点E作CE⊥PB于点E,
由题意可得:PD=110cm,PC=50cm,
∵∠PCB=90°,PC=BC=50cm,
∴∠CPB=∠CBP=45°,∵PE=50cos45°=25(cm),
∵CE⊥PB,PO⊥DO,
∴△PCE∽△PDO,∴=,
=,
解得:PO=55,
∵PB=PC÷cos45°=50,
∴y=BO=5550≈7.1(cm),
答:y的值约为7.1cm;
(3)由(2)可知,在运动过程中始终有:△PCE∽△PDO,
故=,
∵OP=PB+0B=100﹣x+y,
则=,
∵PC=BC,AP=x,BO=y,
∴PE=,
整理可得:y=﹣0.1x+10.
29.解:(1)∵BC=2.0分米,AC=CN+PN=12分米,
∴AB=12﹣2=10(分米),
∴AP的取值范围为:0分米≤AP≤10分米.
(2)∵CN=PN,∠CPN=60°,
∴△PCN等边三角形.
∴CP=6分米.
∴AP=AC﹣PC=12﹣6=6(分米),
即当∠CPN=60°时,AP=6分米;
(3)连接MN、EF,分别交AC于O、H(最大时P与B重合).
由题意PA=12﹣2=10(分米),
∵PM=PN=CM=CN,
∴四边形PNCM是菱形.
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PO==1(分米).
在Rt△MOP中,PM=6分米,
∴MO2=PM2﹣PB2=62﹣12=35,
∵∠ECH=∠MCB,∠EHC=∠MBC=90°,
∴△CMO∽△CEH.
∴=.
∴=()2=,
∴EH2=9?MO2=315
∴S=π?EH2=315π.
同步优生辅导训练(附答案)
1.小亮想用镜子测量一棵松树的高度,如图所示,第一次他把镜子水平放置在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子水平放置在D点,人在G点正好看到树尖A,已知B、C、F、D、H在水平地面的同一直线上,小亮的眼睛距离地面1.7m,得CD=34m,CF=1.7m,DH=3.4m,请你求出松树的高.
2.在学习完北师大教材九年级上册第四章第6节“利用相似三角形测高”后,某数学兴趣小组的3名同学利用课余时间想要测量学校里两棵树的高度,在同一时刻的阳光下,他们合作完成了以下工作:
(1)测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如图1).
(2)测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为4.4米,一级台阶高为0.3米,落在第一级台阶的影子长为0.2米,
(1)在横线上直接填写甲树的高度为
米,
(2)图3为图2的示意图,请利用图3求出乙树的高度.
3.如图,建筑物BC上有一根旗杆AB,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上,已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A、B、C在一条直线上,点C、D、E、G在一条直线上,AC、FD均垂直于CG,请你帮助小芳求出这座建筑物的高BC.
4.新型冠状病毒感染引发“疫情就是命令,现场就是战场”.家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进0.8m到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
5.西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.
6.小胡家阳台上放置了一个晒衣架如图1,如图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面,经测量:AB=CD=150cm,OE=OF=50cm,OB=OD,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=28cm.衣服穿在衣架后,衣架挂钩挂在点A处,衣服垂挂下来,总长度(从点A开始算起)在什么范围内不会拖落到地面?请通过计算说明理由.
7.随着人们对生活环境的要求逐渐提高,环境保护问题受到越来越多人的关注,环保宣传也随处可见.如图,小云想要测量窗外的环保宣传牌AB的高度,她发现早上阳光恰好从窗户的最高点C处射进房间的地板F处,中午阳光恰好从窗户的最低点处射进房间的地板E处,小云测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求环保宣传牌AB的高度.
8.如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
9.如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合:小亮又在点C1处直立高3m的竹竿CD1,然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m,EC1=6m,C1E1=3m,求电线杆AB的高度.
10.周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳蓬的宽度,如图,由于无法直接测量,小凯便在楼前面的地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳蓬A点处:当他位于Q点时,视线从P点通过露台D点正好落在遮阳蓬B点处,这样观测到两个点A,B间的距离即为遮阳蓬的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、PQ、MN均为垂直于EF,MN=PQ,露台的宽CD=GE,测得GE=5米,EN=13.2米,QN=6.2,请你根据以上信息,求出遮阳蓬的宽AB是多少米?(结果精确到0.01米)
11.数学活动小组的小颖、小明和小华利用皮尺和自制的两个直角三角板测量学校旗杆MN的高度,如示意图,△ABC和△A′B′C′是他们自制的直角三角板,且△ABC≌△A′B′C′,小颖和小明分别站在旗杆的左右两侧,小颖将△ABC的直角边AC平行于地面,眼睛通过斜边AB观察,一边观察一边走动,使得A、B、M共线,此时,小华测量小颖距离旗杆的距离DN=19米,小明将△A′B′C′的直角边B′C′平行于地面,眼睛通过斜边B′A′观察,一边观察一边走动,使得B′、A′、M共线,此时,小华测量小明距离旗杆的距离EN=5米,经测量,小颖和小明的眼睛与地面的距离AD=1米,B′E=1.5米,(他们的眼睛与直角三角板顶点A,B′的距离均忽略不计),且AD、MN、B′E均与地面垂直,请你根据测量的数据,计算旗杆MN的高度.
12.太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
13.某学校的学生为了对小雁塔有基本的认识,在老师的带领下对小雁塔进行了测量.测量方法如下:如图,间接测得小雁塔底部点D到地面上一点E的距离为115.2米,小雁塔的顶端为点B,且BD⊥DE,在点E处竖直放一个木棒,其顶端为C,CE=1.72米,在DE的延长线上找一点A,使A、C、B三点在同一直线上,测得AE=4.8米.求小雁塔的高度.
14.我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
求:(1)装饰画与墙壁的夹角∠CAD的度数(精确到1°);
(2)装饰画顶部到墙壁的距离DC(精确到0.01米).
15.如图所示,小明在地面上放置一个平面镜C,选择合适的位置,刚好在平面镜C中看到旗杆DE的顶部,此时小明与平面镜C的水平距离BC为2m,旗杆底部与平面镜的水平距离CE为16m.若小明的眼睛与地面的距离AB为1.6m,试求旗杆DE的高度.
16.20世纪90年代以来,我国户外广告行业取得了突飞猛进的发展,户外广告装置多设立于城市道路、铁路、公路等主要交通干道边上,面向密集的车流和人流.某天,小芳走到如图所示的C处时,看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住,3s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是21.6km/h,假设AB∥PQ,公路宽为10m,求小芳所在C处到公路南侧PQ的距离.
17.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
18.为方便住校生晚自习后回到宿舍就寝,赵化中学新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
19.《铁血红安》在中央一台热播后,吸引了众多游客前往影视基地游玩.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高1.7米.请根据以上数据求出城楼的高度.
20.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.
21.如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.(=1.732,=1.414,=2.449,精确到1米).
22.小明想用镜子测量一棵松树的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子放在D点,人在G点正好看到树尖A.已知小明的眼睛距离地面1.70m,量得CD=12m,CF=1.8m,DH=3.8m.请你求出松树的高.
23.在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
24.雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
25.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
26.刘徽(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是
;
(2)在(1)中提到刘徽的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
27.如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
28.如图1是一个某物体的支架实物图,图2是其右侧部分抽象后的几何图形,其中点C是支杆PD上一可转动点,点P是中间竖杆BA上的一动点,当点P沿BA滑动时,点D随之在地面上滑动,点A是动点P能到达的最顶端位置,当P运动到点A时,PC与BC重合于竖杆BA,经测量PC=BC=50cm,CD=60cm,设AP=xcm,竖杆BA的最下端B到地面的距离BO=ycm.
(1)求AB的长;
(2)当∠PCB=90°时,求y的值;(参考数据:1.414,结果精确到0.1cm)
(3)当点P运动时,试求出y与x的函数关系式.
29.图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米.
(1)求AP长的取值范围;
(2)当∠CPN=60°时,求AP的值;
(3)在阳光垂直照射下,伞张得最开时,求伞下的阴影(假定为圆面)面积S(结果保留π).
参考答案
1.解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH,
∵AB⊥BC,EF⊥BC,GH⊥BC,
∴△BAC∽△FEC、△ADB∽△GDH,
设AB=x,BC=y,
∴,
解得.
答;这棵松树的高为34米.
2.解:(1)设甲树的高度为x米,
根据题意得:=,
解得:x=5.1(米),
故答案为:5.1;
(2)连接AE并延长交BC的延长线于M,延长ED交AB于F,连接AD,如图3所示:
∵CD=0.3m,DE=0.2m,
BC=4.4m,
∴EF=4.4+0.2=4.6(m),
∴=,
∴=,
∴AF=(m),
∴AB=AF+BF=+0.3=6.05(m).
答:乙树的高度为6.05米.
3.解:由题意可得,∠ACE=∠EDF=90°,∠AEC=∠FED,
∴△ACE∽△FDE,
∴,
即,
∴CD=,
由题意可得,∠BCG=∠FDG=90°,∠BGC=∠FGD,
∴△BCG∽△FDG,
∴,
即,
∴6.5BC=4(CD+6.5),
∴6.5BC=4×,
∴BC=14(米),
∴这座建筑物的高BC为14米.
4.解:延长ED交AB于H,延长MQ交BA的延长线于T.
由题意MT=2m,MQ=0.8m,
∴QT=MT﹣MQ=2﹣0.8=1.2(m),
∵四边形BCDH是矩形,
∴DH=BC=300(m),
∵QT∥DH,
∴===,
∵MT∥DE,
∴=,
∴=,
∴EH=500(m),
∴DE=500﹣300=200(m)
5.解:∵△EDC∽△EBA,△FHG∽△FBA,
∴=,=,
∵DC=HG,
∴=,
∴=,
∴CA=106(米),
∵=,
∴=,
∴AB=55(米),
答:大雁塔的高度AB为55米.
6.解:∵AB、CD相交于点O,
∴∠AOC=∠BOD
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠BOD),
同理可证:∠OBD=∠ODB=(180°﹣∠BOD),
∴∠OAC=∠OBD,
∴AC∥BD,
在Rt△OEM中,OM===48(cm),
过点A作AH⊥BD于点H,
同理可证:EF∥BD,
∴∠ABH=∠OEM,则Rt△OEM∽Rt△ABH,
∴=,
∴AH===144(cm),
所以垂挂在衣架上的连衣裙总长度小于144cm时,连衣裙才不会拖落到地面上.
7.解:∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=xm,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴=,
=,
解得:x=10.
经检验:x=10是原方程的解.
答:AB的高度是10m.
8.解:(1)如图1,
∵PM∥BD,
∴△APM∽△ABD,
=,即=,
∴AP=AB,
∵NQ∥AC,
∴△BNQ∽△BCA,
∴=,即=,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴=,即=,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
9.解:∵DC⊥AED1C1⊥AEBA⊥AE
∴DC∥D1C1∥BA,
∴△F1D1N∽△F1BG.
∴.
∵DC∥BA,
∴△FDM∽△FBG.
∴.
∵D1N=DM,
∴,
即.
∴GM=16m.
∵,
∴.
∴BG=13.5m.
∴AB=BG+GA=15(m).
答:电线杆AB的高度为15m.
10.解:延长MP交DE于H,如图,
则HM=EN=13.2米,CD=GE=5米,
MP=NQ=6.2米,
∵CD∥HM,
∴∠ADC=∠DMH,
∴Rt△ACD∽Rt△DHM,
∴==,
∵AB∥MP,
∴△ABD∽△MPD,
∴==,
即=,
解得AB=2.35(米).
答:遮阳篷的宽AB是2.35米.
11.解:过点C作CE'⊥MN于E',过点C′作C′F⊥MN于F,
则E'F=B′E﹣AD=1.5﹣1=0.5(m),AE'=DN=19,B′F=EN=5,
∵△ABC≌△A′B′C′,
∴∠MAE'=∠B′MF,
∵∠AE'M=∠B′FM=90°,
∴△AME'∽△MB'F,
∴,
∴=
∴MF=,
∴MN=MF+FN=11,
答:旗杆MN的高度约为11米.
12.解:∵△EDC∽△EBA,△FHG∽△FBA,
∴=,=,∵DC=HG,
∴=,
∴=,
∴CA=106(米),
∵=,
∴=,
∴AB=55(米),
答:舍利塔的高度AB为55米.
13.解:由题意可得:△AEC∽△ADB,
则=,
故=,
解得:DB=43,
答:小雁塔的高度为43m.
14.解:(1)∵AD=0.66米,
∴AE=AD=0.33米,
在Rt△ABE中,
∵sin∠ABE==,
∴∠ABE≈12°,
∵∠CAD+∠DAB=90°,∠ABE+∠DAB=90°,
∴∠CAD=∠ABE=12°.
∴镜框与墙壁的夹角∠CAD的度数约为12°.
(2)解法一:
在Rt△ACD中,
∵sin∠CAD=,
∴CD=AD?sin∠CAD=0.66×sin12°≈0.14米,
解法二:
∵∠CAD=∠ABE,
∠ACD=∠AEB=90°,
∴△ACD∽△BEA,
∴,
∴,
∴CD≈0.14米.
∴镜框顶部到墙壁的距离CD约是0.14米.
15.解:由题意得∠ACB=∠DCE,
∵∠ABC=∠DEC,
∴△ACB∽△DCE,
∴,
即.
∴DE=12.8
答:旗杆的高度为12.8m.
16.解:设小芳所在C处到公路南侧PQ的距离为xm,
21.6km/h=21.6×=6m/s,
∵AB∥PQ,
∴△CAB∽△CPQ,
∴,
∴=,
∴x=30,
∴小芳所在C处到公路南侧PQ的距离为30m.
17.解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米.
18.解:如图所示:过点E作EB⊥AC于点B,
由题意可得:DC=BE=4.6m,DE=BC=2.5m,
∵同一时刻身高1.5米小刚站立时在太阳光下的影长恰好为1米,
∴==,
解得:AB=6.9,
故AC=AB+BC=6.9+2.5=9.4(m),
答:新安装的照明路灯的灯杆的高度为9.4m.
19.解:过点A作AM⊥EF于点M,交CD于点N,
由题意可得:AN=2m,CN=2﹣1.65=0.35(m),MN=40m,
∵CN∥EM,
∴△ACN∽△AEM,
∴=,
∴=,
解得:EM=7.35,
∵AB=MF=1.65m,
故城楼的高度为:7.35+1.65﹣1.7=7.3(米),
答:城楼的高度为7.3m.
20.解:作DE⊥AB于点E,
根据题意得:=,
=,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
21.解:延长AD交BC于E点,则∠AEB=30°,
作DQ⊥BC于Q,
在Rt△DCQ中,∠DCQ=45°,DC=8,
∴DQ=QC=8sin45°=8×=4,
在Rt△DQE中,QE=≈9.8(米)
∴BE=BC+CQ+QE≈35.5(米)
在Rt△ABE中,AB=BEtan30°≈20(米)
答:旗杆的高度约为20米.
22.解:根据反射定律可以推出∠ACB=∠ECF,∠ADB=∠GDH,
∵AB⊥BC,EF⊥BC,GH⊥BC,
∴△BAC∽△FEC、△ADB∽△GDH,
设AB=x,BC=y
∴,
解得.
答;这棵古松的高约为10.2米
23.解:这种测量方法可行.
理由如下:
设旗杆高AB=x.过F作FG⊥AB于G,交CE于H(如图).
所以△AGF∽△EHF.
因为FD=1.5,GF=27+3=30,HF=3,
所以EH=3.5﹣1.5=2,AG=x﹣1.5.
由△AGF∽△EHF,
得=,
即=,
所以x﹣1.5=20,
解得x=21.5(米)
答:旗杆的高为21.5米.
24.解:由题意知,CD=EF=1.6m,DG=2.8m,DF=1.5m,GH=1.7m,
∴FH=2.8﹣1.5+1.7=3m,
∵AB⊥BH,CD⊥BH,EF⊥BH,
∴△CDG∽△ABG,△EFH∽△ABH,
∴=,=,
∴=,即=,
解得BD=21,
∴,
解得AB=13.6.
即该校旗杆的高度AB为13.6m.
25.解:∵AB⊥BH,CD⊥BH,EF⊥BH,
∴AB∥CD∥EF,
∴△CDG∽△ABG,△EFH∽△ABH,
∴=,=,
∵CD=DG=EF=2m,DF=52m,FH=4m,
∴=,
=,
∴=,
解得BD=52,
∴=,
解得AB=54.
答:建筑物的高为54米.
26.解:(1)《海岛算经》;
(2)由题意,得,AH⊥HG,CB⊥HG,
∴∠AHF=90°,∠CBF=90°,
∴∠AHF=∠CBF,
∵∠AFB=∠CFB,
∴△CBF∽△AHF,
∴=,
同理可得=,
∵BF=123,BD=1000,DG=127,
∴HF=HB+123,HG=HB+1000+127=HB+1127,
∴=,=,
解得HB=30750,HA=753,
答:AH为753丈,HB为30750步.
27.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.5米,EG=FB=2.5米,GH=BD=8米,
∴AG=AB﹣GB=2.4﹣1.5=0.9米,
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH,
∴=,
∴=,
解得:CH=3.78米,
∴DC=CH+DH=3.78+1.5=5.28米.
答:故树高DC为5.28米.
28.解:(1)∵当P运动到点A时,PC与BC重合于竖杆BA,
∴由题意可得:AB=PC+BC=50+50=100(cm);
(2)如图,过点E作CE⊥PB于点E,
由题意可得:PD=110cm,PC=50cm,
∵∠PCB=90°,PC=BC=50cm,
∴∠CPB=∠CBP=45°,∵PE=50cos45°=25(cm),
∵CE⊥PB,PO⊥DO,
∴△PCE∽△PDO,∴=,
=,
解得:PO=55,
∵PB=PC÷cos45°=50,
∴y=BO=5550≈7.1(cm),
答:y的值约为7.1cm;
(3)由(2)可知,在运动过程中始终有:△PCE∽△PDO,
故=,
∵OP=PB+0B=100﹣x+y,
则=,
∵PC=BC,AP=x,BO=y,
∴PE=,
整理可得:y=﹣0.1x+10.
29.解:(1)∵BC=2.0分米,AC=CN+PN=12分米,
∴AB=12﹣2=10(分米),
∴AP的取值范围为:0分米≤AP≤10分米.
(2)∵CN=PN,∠CPN=60°,
∴△PCN等边三角形.
∴CP=6分米.
∴AP=AC﹣PC=12﹣6=6(分米),
即当∠CPN=60°时,AP=6分米;
(3)连接MN、EF,分别交AC于O、H(最大时P与B重合).
由题意PA=12﹣2=10(分米),
∵PM=PN=CM=CN,
∴四边形PNCM是菱形.
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PO==1(分米).
在Rt△MOP中,PM=6分米,
∴MO2=PM2﹣PB2=62﹣12=35,
∵∠ECH=∠MCB,∠EHC=∠MBC=90°,
∴△CMO∽△CEH.
∴=.
∴=()2=,
∴EH2=9?MO2=315
∴S=π?EH2=315π.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
