人教版数学九年级上册 25.2用列表法求概率(第一课时) 教案
文档属性
| 名称 | 人教版数学九年级上册 25.2用列表法求概率(第一课时) 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览

文档简介
教师姓名
单位名称
填写时间
2020年8月26日
学科
数学
年级/册
九年级上册
教材版本
人教版
课题名称
25.2
用列举法求概率(第一课时)
难点名称
如何正确使用列表法
难点分析
从知识角度分析为什么难
相对于直接列举法,列表法体现了“分步”分析问题的重要作用。列表法用过表格的首行和首列同时分析了两个元素的所有情况,组合展示的试验的所有可能的结果。“分步”思想将在之后的“树状图法”中得到进一步应用。
从学生角度分析为什么难
试验涉及到两个因素,且每个因素取值个数较多时,学生很难通过直接列举法,做到不重不漏的列举出所有结果,学生缺少“分步”分析问题的意识。在利用列表法时,因为没有真正理解列表法,所以在遇到例题以外的问题时,不能正确使用列表法解决问题。
难点教学方法
通过掷两枚骰子的游戏,让同学们感受到“分步”分析问题可以降低题目的复杂度,而且展示了列表法的对于展示试验所有结果的直观性,以及帮助学生快速找到需要的结果,进而求出概率解决问题。
教学环节
教学过程
导入
想一想
(1)如果让你抛掷一枚质地均匀的硬币,观察向上一面,可能出现的结果:
(2)同时掷一枚质地均匀的骰子,观察向上一面的情况,可能出现的结果有:
;
(3)同时掷两枚质地均匀的硬币,观察向上一面的情况,可能出现的结果有:
;
(4)同时掷两枚质地均匀的骰子,观察向上一面的情况,可能出现的结果有哪些呢?
(增加试验元素,引导学生发现直接列举法无法快速做到不重不漏的罗列出所有实验结果,进而思考新的方法)
知识讲解
(难点突破)
例1
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上、一枚硬币反面向上.
思考:为了不重不漏地列举所有可能出现的结果,你有什么好办法吗?
我们可以设其中一枚为A,另一枚为B
法一:直接列举法(A正、B正)(A正、B反)(A反、B正)(A反、B反)
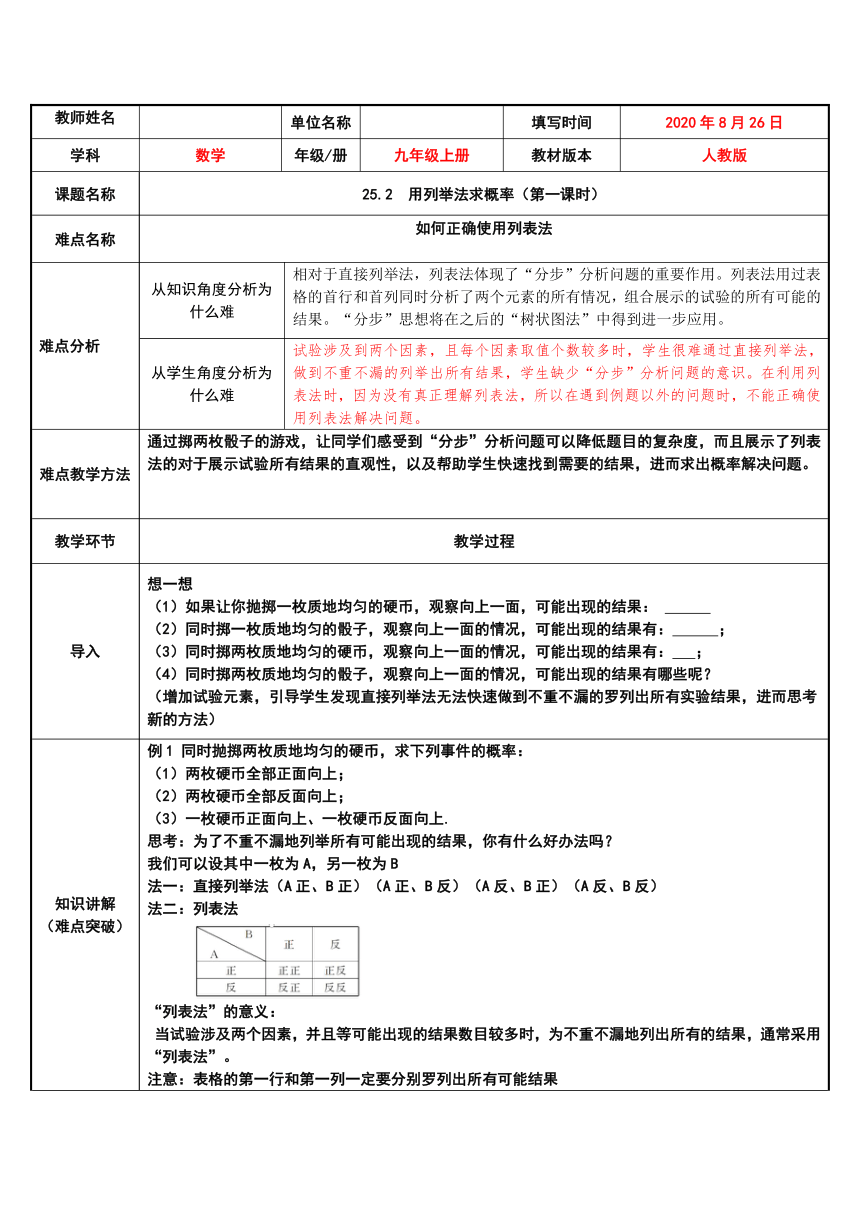
法二:列表法
“列表法”的意义:
当试验涉及两个因素,并且等可能出现的结果数目较多时,为不重不漏地列出所有的结果,通常采用“列表法”。
注意:表格的第一行和第一列一定要分别罗列出所有可能结果
例2
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
引导学生发现本题试验涉及两个因素,并且等可能出现的结果数目较多,为不重不漏地列出所有的结果,我们可以“列表法”。
通过例题的解决,让学生们发现列表法不仅可以帮我们快速罗列出所有可能发生的结果,还可以快速找到符合题目要求的结果,进而解决概率问题。
归纳:当一个事件要涉及两个因素并且可能出现的结果数目较多时,通常采用列表法。
运用列表法求概率的步骤如下:
①列表;
②通过表格确定所有可能出现的结果数n,发生规定事件的结果数
m;
③利用P(A)=
m/n
计算事件的概率。
追问:如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
再次体现列表法能帮助我们“分步”分析问题。
课堂练习
(难点巩固)
1.如果有两组相同的牌,它们的牌面数字分别是1,2,3,4,那么从每组牌中各摸出一张牌。:
(1)两张牌的牌面数字之和等于6的概率是多少呢?
(2)从所列表格中你还能提出问题吗?
2.袋子中装有红、绿各一个小球,除颜色外无其他差别,随机摸出1个小球后,放回并摇匀,再随机摸出一个,求下列事件的概率:
(1)第一次摸到红球,第二次摸到绿球;
(2)两次都摸到相同颜色的小球;
(3)两次摸到的球中有一个绿球和一个红球。
小结
1.用列表法求概率应注意哪些问题?
2.列表法适用于解决哪类概率求解问题?使用列表法有哪些注意事项?
单位名称
填写时间
2020年8月26日
学科
数学
年级/册
九年级上册
教材版本
人教版
课题名称
25.2
用列举法求概率(第一课时)
难点名称
如何正确使用列表法
难点分析
从知识角度分析为什么难
相对于直接列举法,列表法体现了“分步”分析问题的重要作用。列表法用过表格的首行和首列同时分析了两个元素的所有情况,组合展示的试验的所有可能的结果。“分步”思想将在之后的“树状图法”中得到进一步应用。
从学生角度分析为什么难
试验涉及到两个因素,且每个因素取值个数较多时,学生很难通过直接列举法,做到不重不漏的列举出所有结果,学生缺少“分步”分析问题的意识。在利用列表法时,因为没有真正理解列表法,所以在遇到例题以外的问题时,不能正确使用列表法解决问题。
难点教学方法
通过掷两枚骰子的游戏,让同学们感受到“分步”分析问题可以降低题目的复杂度,而且展示了列表法的对于展示试验所有结果的直观性,以及帮助学生快速找到需要的结果,进而求出概率解决问题。
教学环节
教学过程
导入
想一想
(1)如果让你抛掷一枚质地均匀的硬币,观察向上一面,可能出现的结果:
(2)同时掷一枚质地均匀的骰子,观察向上一面的情况,可能出现的结果有:
;
(3)同时掷两枚质地均匀的硬币,观察向上一面的情况,可能出现的结果有:
;
(4)同时掷两枚质地均匀的骰子,观察向上一面的情况,可能出现的结果有哪些呢?
(增加试验元素,引导学生发现直接列举法无法快速做到不重不漏的罗列出所有实验结果,进而思考新的方法)
知识讲解
(难点突破)
例1
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上、一枚硬币反面向上.
思考:为了不重不漏地列举所有可能出现的结果,你有什么好办法吗?
我们可以设其中一枚为A,另一枚为B
法一:直接列举法(A正、B正)(A正、B反)(A反、B正)(A反、B反)
法二:列表法
“列表法”的意义:
当试验涉及两个因素,并且等可能出现的结果数目较多时,为不重不漏地列出所有的结果,通常采用“列表法”。
注意:表格的第一行和第一列一定要分别罗列出所有可能结果
例2
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是9;
(3)至少有一枚骰子的点数为2.
引导学生发现本题试验涉及两个因素,并且等可能出现的结果数目较多,为不重不漏地列出所有的结果,我们可以“列表法”。
通过例题的解决,让学生们发现列表法不仅可以帮我们快速罗列出所有可能发生的结果,还可以快速找到符合题目要求的结果,进而解决概率问题。
归纳:当一个事件要涉及两个因素并且可能出现的结果数目较多时,通常采用列表法。
运用列表法求概率的步骤如下:
①列表;
②通过表格确定所有可能出现的结果数n,发生规定事件的结果数
m;
③利用P(A)=
m/n
计算事件的概率。
追问:如果把例2中的“同时掷两枚质地均匀的骰子”改为“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
再次体现列表法能帮助我们“分步”分析问题。
课堂练习
(难点巩固)
1.如果有两组相同的牌,它们的牌面数字分别是1,2,3,4,那么从每组牌中各摸出一张牌。:
(1)两张牌的牌面数字之和等于6的概率是多少呢?
(2)从所列表格中你还能提出问题吗?
2.袋子中装有红、绿各一个小球,除颜色外无其他差别,随机摸出1个小球后,放回并摇匀,再随机摸出一个,求下列事件的概率:
(1)第一次摸到红球,第二次摸到绿球;
(2)两次都摸到相同颜色的小球;
(3)两次摸到的球中有一个绿球和一个红球。
小结
1.用列表法求概率应注意哪些问题?
2.列表法适用于解决哪类概率求解问题?使用列表法有哪些注意事项?
同课章节目录
