11.1.1 三角形的边-2021-2022学年人教版八年级数学上册教学课件(22张)
文档属性
| 名称 | 11.1.1 三角形的边-2021-2022学年人教版八年级数学上册教学课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 09:59:12 | ||
图片预览






文档简介
(共22张PPT)
第11章
三角形
人教版八年级(上)数学
11.1
与三角形有关的线段
探究新知
知识归纳
典型例题
当堂训练
课堂小结
导入新课
11.1.1
三角形的边
情境导入
【问题】
(1)从古埃及的金字塔到现代的飞机;
从宏伟的建筑物到微小的分子结构,都有什么样的形象?
(2)在我们的生活中有没有这样的形象呢?试举例.
三角形的概念
01
三角形的分类
02
三角形的三边关系
03
知识点
【问题】观察下面三角形的形成过程,说一说什么叫三角形?
A
B
C
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
1.定义:
要点归纳
知识点一
三角形的概念
三角形的顶点:__________;
三角形的边:____________;
三角形的内角(简称为三角形的角)____________.
A、B、C
AB、BC、CA
∠A,∠B,∠C
三角形用符号“△”表示;
记作“△ABC”,读作“三角形ABC”;
还可记作△BCA,△CAB,△ACB等.
2.基本要素:
3.表示方法:
a
A
C
B
b
c
【特别规定】三角形ABC的三边,一般的顶点A、B、C所对的边分别记作_________,
a、b、c
要点归纳
知识点一
三角形的概念
【例1】辨一辨下列图形符合三角形的定义吗?
不符合
不符合
三角形应满足以下两个条件:
1.位置关系:_______________;
2.联接方式:_______________.
要点提醒
不在同一直线上
首尾顺次相接
不符合
典型例题
知识点一
三角形的概念
【找一找】
(1)图中有几个三角形?表示出这些三角形?
5个,分别是△ABE,△ABC,△BEC,△BCD,△ECD.
A
B
C
D
E
(2)以AB为边的三角形有哪些?
△ABC,△ABE.
(3)以E为顶点的三角形有哪些?
△ABE,△BCE,△CDE.
(4)以∠D为角的三角形有哪些?
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD,△DEC.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
基础训练
知识点一
三角形的概念
三角形的概念
01
三角形的分类
02
三角形的三边关系
03
知识点
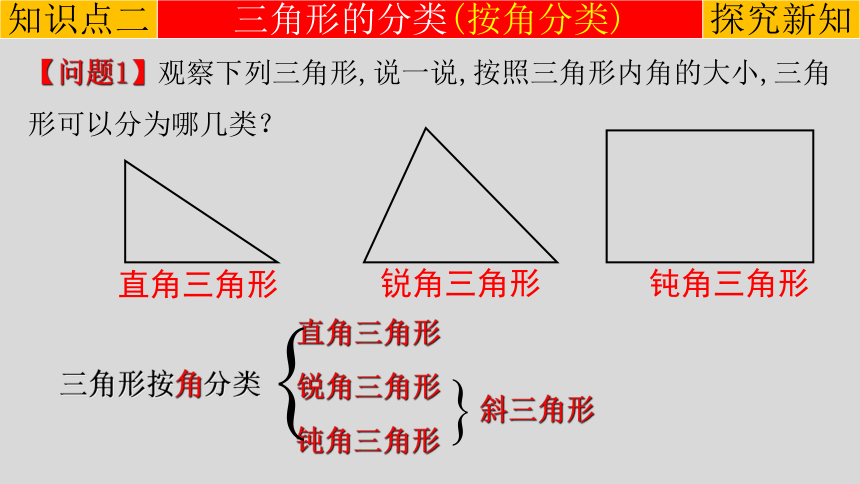
【问题1】观察下列三角形,说一说,按照三角形内角的大小,三角形可以分为哪几类?
直角三角形
锐角三角形
钝角三角形
直角三角形
锐角三角形
三角形按角分类
钝角三角形
斜三角形
探究新知
知识点二
三角形的分类(按角分类)
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
【问题2】你能从边的角度找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
腰
底角
三条边各不相等的三角形叫做不等边三角形
有两条边相等的三角形叫做等腰三角形
三条边都相等的三角形叫做等边三角形
探究新知
知识点二
三角形的分类(按边分类)
【思考】等边三角形和等腰三角形之间有什么关系?
不等边三角形
等腰三角形
腰和底不等的等腰三角形
等边三角形(三边都相等)
三角形按边分类
要点归纳
知识点二
三角形的分类(按边分类)
判断:
(2)等边三角形是特殊的等腰三角形.
(
)
(1)一个钝角三角形一定不是等腰三角形.(
)
√
×
(3)等腰三角形的腰和底一定不相等.
(
)
×
(4)等边三角形是锐角三角形.
(
)
(5)直角三角形一定不是等腰三角形.
(
)
×
√
基础训练
知识点二
三角形的分类
三角形的概念
01
三角形的分类
02
三角形的三边关系
03
知识点
【问题】在A点的小狗,为了尽快吃到B点的香肠,它选择A
B路线,而不选
择A
C
B路线,难道小狗
也懂数学?
C
B
A
AC+BC>AB
同理可得:
AB+BC>AC
AC+AB>BC
理由:
两点之间线段最短
AC>AB-BC
BC>AB-AC
AB>AC-BC
BC>AC-AB
AC>BC-AB
BC>BC-AC
2.三角形两边的差小于第三边.
1.三角形两边的和大于第三边;
探究新知
知识点三
三角形的三边关系
解:取长度为2cm的木棒时,∵2+5=7<8,∴它们不能摆成三角形;
【例3-1】有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可.
要点提醒
取长度为13cm的木棒时,∵5+8=13,∴它们也不能摆成三角形.
典型例题
知识点三
三角形的三边关系
【例3-2】一个三角形的三边长分别为4,7,x,则x的取值范围是(
)A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
解析:∵三角形的三边长分别为4,7,x,
A
判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
要点提醒
∴7-4<x<7+4,即3<x<11.
典型例题
知识点三
三角形的三边关系
【例3-3】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么
?
解:(1)设底边长为xcm,则腰长为2xcm,x+2x+2x=18.
综上所述,可以围成底边长是4cm的等腰三角形.
(2)①若底边长为4cm,设腰长为xcm,则有4+2x=18.解得:x=7.
②若腰长为4cm,设底边长为xcm,则有2×4+x=18.解得:x=10.
∵4+4<10,不符合三角形两边的和大于第三边,
∴不能围成腰长是4cm的等腰三角形.
解得:x=3.6.所以三边长分别为3.6cm,7.2cm,7.2cm.
典型例题
知识点三
三角形的三边关系
【例3-4】如图,D是△ABC
的边AC上一点,AD=BD,试判断AC与BC
的大小.
解:在△BDC
中,
BD+DC>BC.
又∵AD=BD,
∴BD+DC=AD+DC=AC,
∴AC>BC.
A
C
D
B
典型例题
知识点三
三角形的三边关系
1.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成___个三角形.
2.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为___________.
3.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长为______.
3
22cm
18cm或21cm
基础训练
知识点三
三角形的三边关系
解:设第三边长为x,根据三角形的三边关系,可得,
7-2<x<7+2,即5<x<9,
又∵x为奇数,则第三边的长为7.
4.若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长
基础训练
知识点三
三角形的三边关系
5.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得:
拓展提升
知识点三
三角形的三边关系
=3c+a-b.
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类分类
不重不漏
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|b,x为第三边)
应用
课堂小结
第11章
三角形
人教版八年级(上)数学
11.1
与三角形有关的线段
探究新知
知识归纳
典型例题
当堂训练
课堂小结
导入新课
11.1.1
三角形的边
情境导入
【问题】
(1)从古埃及的金字塔到现代的飞机;
从宏伟的建筑物到微小的分子结构,都有什么样的形象?
(2)在我们的生活中有没有这样的形象呢?试举例.
三角形的概念
01
三角形的分类
02
三角形的三边关系
03
知识点
【问题】观察下面三角形的形成过程,说一说什么叫三角形?
A
B
C
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
1.定义:
要点归纳
知识点一
三角形的概念
三角形的顶点:__________;
三角形的边:____________;
三角形的内角(简称为三角形的角)____________.
A、B、C
AB、BC、CA
∠A,∠B,∠C
三角形用符号“△”表示;
记作“△ABC”,读作“三角形ABC”;
还可记作△BCA,△CAB,△ACB等.
2.基本要素:
3.表示方法:
a
A
C
B
b
c
【特别规定】三角形ABC的三边,一般的顶点A、B、C所对的边分别记作_________,
a、b、c
要点归纳
知识点一
三角形的概念
【例1】辨一辨下列图形符合三角形的定义吗?
不符合
不符合
三角形应满足以下两个条件:
1.位置关系:_______________;
2.联接方式:_______________.
要点提醒
不在同一直线上
首尾顺次相接
不符合
典型例题
知识点一
三角形的概念
【找一找】
(1)图中有几个三角形?表示出这些三角形?
5个,分别是△ABE,△ABC,△BEC,△BCD,△ECD.
A
B
C
D
E
(2)以AB为边的三角形有哪些?
△ABC,△ABE.
(3)以E为顶点的三角形有哪些?
△ABE,△BCE,△CDE.
(4)以∠D为角的三角形有哪些?
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD,△DEC.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
基础训练
知识点一
三角形的概念
三角形的概念
01
三角形的分类
02
三角形的三边关系
03
知识点
【问题1】观察下列三角形,说一说,按照三角形内角的大小,三角形可以分为哪几类?
直角三角形
锐角三角形
钝角三角形
直角三角形
锐角三角形
三角形按角分类
钝角三角形
斜三角形
探究新知
知识点二
三角形的分类(按角分类)
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
【问题2】你能从边的角度找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
腰
底角
三条边各不相等的三角形叫做不等边三角形
有两条边相等的三角形叫做等腰三角形
三条边都相等的三角形叫做等边三角形
探究新知
知识点二
三角形的分类(按边分类)
【思考】等边三角形和等腰三角形之间有什么关系?
不等边三角形
等腰三角形
腰和底不等的等腰三角形
等边三角形(三边都相等)
三角形按边分类
要点归纳
知识点二
三角形的分类(按边分类)
判断:
(2)等边三角形是特殊的等腰三角形.
(
)
(1)一个钝角三角形一定不是等腰三角形.(
)
√
×
(3)等腰三角形的腰和底一定不相等.
(
)
×
(4)等边三角形是锐角三角形.
(
)
(5)直角三角形一定不是等腰三角形.
(
)
×
√
基础训练
知识点二
三角形的分类
三角形的概念
01
三角形的分类
02
三角形的三边关系
03
知识点
【问题】在A点的小狗,为了尽快吃到B点的香肠,它选择A
B路线,而不选
择A
C
B路线,难道小狗
也懂数学?
C
B
A
AC+BC>AB
同理可得:
AB+BC>AC
AC+AB>BC
理由:
两点之间线段最短
AC>AB-BC
BC>AB-AC
AB>AC-BC
BC>AC-AB
AC>BC-AB
BC>BC-AC
2.三角形两边的差小于第三边.
1.三角形两边的和大于第三边;
探究新知
知识点三
三角形的三边关系
解:取长度为2cm的木棒时,∵2+5=7<8,∴它们不能摆成三角形;
【例3-1】有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可.
要点提醒
取长度为13cm的木棒时,∵5+8=13,∴它们也不能摆成三角形.
典型例题
知识点三
三角形的三边关系
【例3-2】一个三角形的三边长分别为4,7,x,则x的取值范围是(
)A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
解析:∵三角形的三边长分别为4,7,x,
A
判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
要点提醒
∴7-4<x<7+4,即3<x<11.
典型例题
知识点三
三角形的三边关系
【例3-3】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么
?
解:(1)设底边长为xcm,则腰长为2xcm,x+2x+2x=18.
综上所述,可以围成底边长是4cm的等腰三角形.
(2)①若底边长为4cm,设腰长为xcm,则有4+2x=18.解得:x=7.
②若腰长为4cm,设底边长为xcm,则有2×4+x=18.解得:x=10.
∵4+4<10,不符合三角形两边的和大于第三边,
∴不能围成腰长是4cm的等腰三角形.
解得:x=3.6.所以三边长分别为3.6cm,7.2cm,7.2cm.
典型例题
知识点三
三角形的三边关系
【例3-4】如图,D是△ABC
的边AC上一点,AD=BD,试判断AC与BC
的大小.
解:在△BDC
中,
BD+DC>BC.
又∵AD=BD,
∴BD+DC=AD+DC=AC,
∴AC>BC.
A
C
D
B
典型例题
知识点三
三角形的三边关系
1.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成___个三角形.
2.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为___________.
3.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长为______.
3
22cm
18cm或21cm
基础训练
知识点三
三角形的三边关系
解:设第三边长为x,根据三角形的三边关系,可得,
7-2<x<7+2,即5<x<9,
又∵x为奇数,则第三边的长为7.
4.若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长
基础训练
知识点三
三角形的三边关系
5.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得:
拓展提升
知识点三
三角形的三边关系
=3c+a-b.
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类分类
不重不漏
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|
应用
课堂小结
