鲁教版(五四制)七上3.1.2探索勾股定理 教案(表格式)
文档属性
| 名称 | 鲁教版(五四制)七上3.1.2探索勾股定理 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 00:00:00 | ||
图片预览



文档简介
3.1.2验证勾股定理
教学设计
第一部分 教材分析
项 目
内 容
设计意图
教学内容
验证勾股定理
教学目标
让学生经历勾股定理的验证过程,掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题,体会数形结合的思想和从特殊到一般的思想。
通这对勾股定理的验证,培养探究能力和合作精神,并通过应用勾股定理解决实际问题,培养应用数学的意识。
教学重点
用面积法验证勾股定理,应用勾股定理解决简单的实际问题。
让学生体会数形结合的思想
教学难点
验证勾股定理
培养学生小组合作的团结精神
第二部分 课堂教学
教学环节
教学过程
设计意图
复习设疑,激趣引入
(1)勾股定理的内容是什么?(2)上节课我们仅仅是通过测量和数格子,对具体的直角三角形探索发现了勾股定理,对一般的直角三角形,勾股定理是否成立呢?事实上,现在已经有400多种勾股定理的验证方法,你想用自己的方法验证勾股定理吗?
(1)复习勾股定理内容;(2)回顾上一节课探索过程,强调仍需对一般的直角三角形进行验证,培养学生严谨的科学态度;(3)介绍世界上有数百种验证方法,当学生听到有数百种验证方法时,马上就有了去寻求属于自己的方法的渴望,激发求知欲。
小组合作
(1)请你利用平板上的四个全等的直角三角形,拼出一个以斜边为边长的正方形。(请每位同学用6分钟时间独立拼图,然后再4人小组讨论,并选出一名代表发言。)(2)学生通过小组讨论可能得到下面两个图形:(若学生没能得出图形,同组内同学演示给其他同学看)
(1)为了让学生在活动中体会图形的构成,既为勾股定理的验证作铺垫,同时也培养学生的动手能力、解决实际问题的能力。(2)通过小组合作,培养学生合作精神和表达能力。(3)考虑学生能力水平有限,万一学生得不出图形来,在这里老师可以指导学生合作互助,使抽象具体化,很直观,学生很容易懂得。
自主探索
(1)你能用两种方法表示图1的正方形的面积吗?正方形的面积可以表示为:__________________又可以表示为:__________________(2)对比两种表示方法,它们的关系是___________,你能利用这个关系得到勾股定理吗?(学生先独立思考,再4人小组交流,交流时,每个同学都要说出自己的理由。)
(1)学生在教师的层层设问引导下完成对勾股定理的验证,完成本节课的一个重点内容。(2)学生通过先拼图从图形上感知,再分析面积,得到验证的方法,使学生积累的验证的经验,为图2的独立证明作下一步的铺垫。
自主尝试
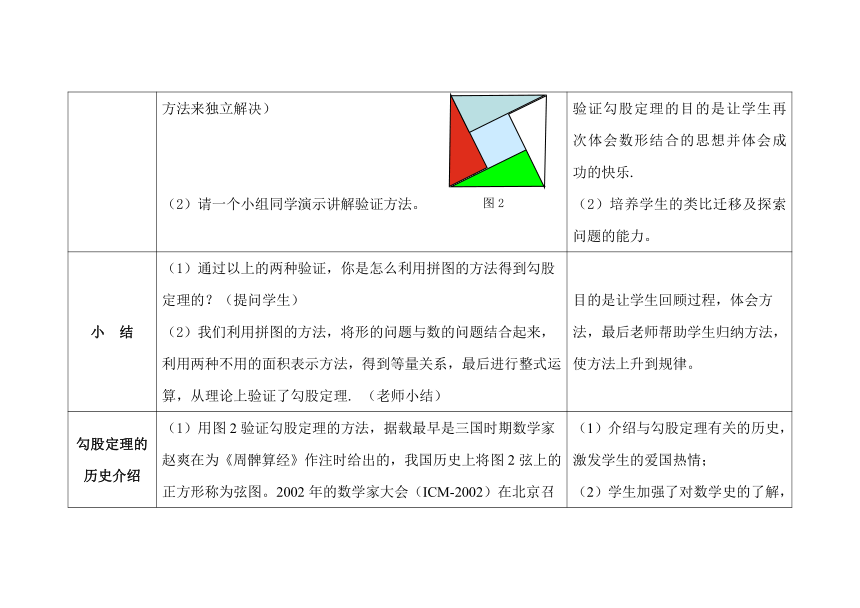
(1)你能利用图2验证勾股定理吗?(提示:利用图1的验证方法来独立解决)(2)请一个小组同学演示讲解验证方法。
(1)让学生利用另一个拼图独立验证勾股定理的目的是让学生再次体会数形结合的思想并体会成功的快乐.(2)培养学生的类比迁移及探索问题的能力。
小
结
(1)通过以上的两种验证,你是怎么利用拼图的方法得到勾股定理的?(提问学生)(2)我们利用拼图的方法,将形的问题与数的问题结合起来,利用两种不用的面积表示方法,得到等量关系,最后进行整式运算,从理论上验证了勾股定理.
(老师小结)
目的是让学生回顾过程,体会方法,最后老师帮助学生归纳方法,使方法上升到规律。
勾股定理的历史介绍
(1)用图2验证勾股定理的方法,据载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的,我国历史上将图2弦上的正方形称为弦图。2002年的数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的弦图,这既标志着中国古代的数学成就
,又像一只转动的风车,欢迎来自世界各地的数学家们!
(1)介绍与勾股定理有关的历史,激发学生的爱国热情;(2)学生加强了对数学史的了解,培养学习数学的兴趣。
学以致用
(先让学生尝试独立完成,然后老师点评,给出规范格式)例1:我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距离400米,10秒后,汽车与他相距离500米,你能帮小玉计算敌方汽车的速度吗?解:在中,由勾股定理得:
敌方汽车10秒行驶了300米,那么它1小时行驶的距离为:,即它行驶的速度为108千米/时。
(1)初步运用勾股定理解决实际问题,培养学生应用数学的意识和能力;(2)体会勾股定理的应用价值。(3)通过例题的讲解,规范学生的书写格式。
巩固练习
1.甲乙两人从同一点出发,甲往东走了4km,乙往南走了3km,这时甲、乙两人相距
.2.如图,小张为测量校园内池塘A,B两点的距离,他在池塘边选定一点C,使∠ABC=90°,并测得AC长26m,BC长24m,则A,B两点间的距离为
.3.观察下图,用数格子的方法求出a2,b2,c2的大小,并完成下列填空。
在例题的基础上进行拓展,训练学生将实际问题转化为数学问题,再运用勾股定理解决问题.同时,以练习的形式引导学生发现锐角三角形和钝角三角形相应的三边关系,与直角三角形融为一体,形成对本部分内容的整体认知,进一步加深对勾股定理的认识,为后续直角三角形的判别打下基础。
延伸拓展
在四个直角三角形拼图的基础上进行延伸拓展,寻求解决问题的不同办法,发散思维。提出问题,供学生课下思考和探究,给学生提供了自主发展的空间,引导学生思考知识方法之间的内在联系,形成对本部分内容的整体认知。
课堂小结
(1)通过这节课的学习,你有什么样的收获?学生共同畅谈收获。(2)在验证勾股定理的过程中,我们运用了什么方法?(3)在利用拼图验证勾股定理时,抓住什么等量关系?(4)利用勾股定理解决问题时,格式是怎么样的?
(1)归纳出本节课的知识要点,数形结合的思想方法;(2)教师了解学生对本节课的感受并进行总结;(3)培养学生的归纳概括能力.
作业布置
(1)课本P72
数学理解
勾股定理的总统验证方法(必做)(2)课本P72
习题3.2
第一题
(选做)(3)预习课本P73~P75(必做)
(1)巩固本节课的内容。(2)充分发挥勾股定理的育人价值。(3)培养学生提前预习的习惯。(4)分层作业,使优生得到更好的发挥。
c
a
b
图2
图1
图2
a
a
b
b
c
c
教学设计
第一部分 教材分析
项 目
内 容
设计意图
教学内容
验证勾股定理
教学目标
让学生经历勾股定理的验证过程,掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题,体会数形结合的思想和从特殊到一般的思想。
通这对勾股定理的验证,培养探究能力和合作精神,并通过应用勾股定理解决实际问题,培养应用数学的意识。
教学重点
用面积法验证勾股定理,应用勾股定理解决简单的实际问题。
让学生体会数形结合的思想
教学难点
验证勾股定理
培养学生小组合作的团结精神
第二部分 课堂教学
教学环节
教学过程
设计意图
复习设疑,激趣引入
(1)勾股定理的内容是什么?(2)上节课我们仅仅是通过测量和数格子,对具体的直角三角形探索发现了勾股定理,对一般的直角三角形,勾股定理是否成立呢?事实上,现在已经有400多种勾股定理的验证方法,你想用自己的方法验证勾股定理吗?
(1)复习勾股定理内容;(2)回顾上一节课探索过程,强调仍需对一般的直角三角形进行验证,培养学生严谨的科学态度;(3)介绍世界上有数百种验证方法,当学生听到有数百种验证方法时,马上就有了去寻求属于自己的方法的渴望,激发求知欲。
小组合作
(1)请你利用平板上的四个全等的直角三角形,拼出一个以斜边为边长的正方形。(请每位同学用6分钟时间独立拼图,然后再4人小组讨论,并选出一名代表发言。)(2)学生通过小组讨论可能得到下面两个图形:(若学生没能得出图形,同组内同学演示给其他同学看)
(1)为了让学生在活动中体会图形的构成,既为勾股定理的验证作铺垫,同时也培养学生的动手能力、解决实际问题的能力。(2)通过小组合作,培养学生合作精神和表达能力。(3)考虑学生能力水平有限,万一学生得不出图形来,在这里老师可以指导学生合作互助,使抽象具体化,很直观,学生很容易懂得。
自主探索
(1)你能用两种方法表示图1的正方形的面积吗?正方形的面积可以表示为:__________________又可以表示为:__________________(2)对比两种表示方法,它们的关系是___________,你能利用这个关系得到勾股定理吗?(学生先独立思考,再4人小组交流,交流时,每个同学都要说出自己的理由。)
(1)学生在教师的层层设问引导下完成对勾股定理的验证,完成本节课的一个重点内容。(2)学生通过先拼图从图形上感知,再分析面积,得到验证的方法,使学生积累的验证的经验,为图2的独立证明作下一步的铺垫。
自主尝试
(1)你能利用图2验证勾股定理吗?(提示:利用图1的验证方法来独立解决)(2)请一个小组同学演示讲解验证方法。
(1)让学生利用另一个拼图独立验证勾股定理的目的是让学生再次体会数形结合的思想并体会成功的快乐.(2)培养学生的类比迁移及探索问题的能力。
小
结
(1)通过以上的两种验证,你是怎么利用拼图的方法得到勾股定理的?(提问学生)(2)我们利用拼图的方法,将形的问题与数的问题结合起来,利用两种不用的面积表示方法,得到等量关系,最后进行整式运算,从理论上验证了勾股定理.
(老师小结)
目的是让学生回顾过程,体会方法,最后老师帮助学生归纳方法,使方法上升到规律。
勾股定理的历史介绍
(1)用图2验证勾股定理的方法,据载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的,我国历史上将图2弦上的正方形称为弦图。2002年的数学家大会(ICM-2002)在北京召开,这届大会会标的中央图案正是经过艺术处理的弦图,这既标志着中国古代的数学成就
,又像一只转动的风车,欢迎来自世界各地的数学家们!
(1)介绍与勾股定理有关的历史,激发学生的爱国热情;(2)学生加强了对数学史的了解,培养学习数学的兴趣。
学以致用
(先让学生尝试独立完成,然后老师点评,给出规范格式)例1:我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距离400米,10秒后,汽车与他相距离500米,你能帮小玉计算敌方汽车的速度吗?解:在中,由勾股定理得:
敌方汽车10秒行驶了300米,那么它1小时行驶的距离为:,即它行驶的速度为108千米/时。
(1)初步运用勾股定理解决实际问题,培养学生应用数学的意识和能力;(2)体会勾股定理的应用价值。(3)通过例题的讲解,规范学生的书写格式。
巩固练习
1.甲乙两人从同一点出发,甲往东走了4km,乙往南走了3km,这时甲、乙两人相距
.2.如图,小张为测量校园内池塘A,B两点的距离,他在池塘边选定一点C,使∠ABC=90°,并测得AC长26m,BC长24m,则A,B两点间的距离为
.3.观察下图,用数格子的方法求出a2,b2,c2的大小,并完成下列填空。
在例题的基础上进行拓展,训练学生将实际问题转化为数学问题,再运用勾股定理解决问题.同时,以练习的形式引导学生发现锐角三角形和钝角三角形相应的三边关系,与直角三角形融为一体,形成对本部分内容的整体认知,进一步加深对勾股定理的认识,为后续直角三角形的判别打下基础。
延伸拓展
在四个直角三角形拼图的基础上进行延伸拓展,寻求解决问题的不同办法,发散思维。提出问题,供学生课下思考和探究,给学生提供了自主发展的空间,引导学生思考知识方法之间的内在联系,形成对本部分内容的整体认知。
课堂小结
(1)通过这节课的学习,你有什么样的收获?学生共同畅谈收获。(2)在验证勾股定理的过程中,我们运用了什么方法?(3)在利用拼图验证勾股定理时,抓住什么等量关系?(4)利用勾股定理解决问题时,格式是怎么样的?
(1)归纳出本节课的知识要点,数形结合的思想方法;(2)教师了解学生对本节课的感受并进行总结;(3)培养学生的归纳概括能力.
作业布置
(1)课本P72
数学理解
勾股定理的总统验证方法(必做)(2)课本P72
习题3.2
第一题
(选做)(3)预习课本P73~P75(必做)
(1)巩固本节课的内容。(2)充分发挥勾股定理的育人价值。(3)培养学生提前预习的习惯。(4)分层作业,使优生得到更好的发挥。
c
a
b
图2
图1
图2
a
a
b
b
c
c
