鲁教版(五四制)七上3.3.1 勾股定理的应用举例 教案(表格式)
文档属性
| 名称 | 鲁教版(五四制)七上3.3.1 勾股定理的应用举例 教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 00:00:00 | ||
图片预览

文档简介
义务教育教科书(鲁教版)(五四制)数学七年级上册第三章第三节
《勾股定理的应用举例》教学设计
第一课时
教学目标
知识与能力:能运用勾股定理及直角三角形的判别条件(即勾股定理的逆定理)解决简单的实际问题.过程与方法:1.学会观察图形,勇于探索图形间的关系,培养学生的空间观念.2.在将实际问题抽象成几何图形过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.情感、态度、价值观:1.通过有趣的问题提高学习数学的兴趣.2.在解决实际问题的过程中,体验数学学习的实用性,体现人人都学有用的数学.
重难点
教学重点:探索、发现给定事物中隐含的勾股定理及其逆及理,并用它们解决生活实际问题.教学难点:利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题.
学情分析
本节位于七年级上册教材第三章第3节,在前面学习了应用勾股定理及勾股定理的逆定理的基础之上,围绕勾股定理及其逆定理,按照“问题情景—建立模型—解释—应用与拓展”的模式展开活动,,学生能够通过简单操作发现在圆柱侧面找最短路径方法,会利用勾股定理解决问题,初步感受应用勾股定理解决问题的思路,为后面探究它的应用做铺垫本节课的综合性和拓展性较强,教材图文并茂,既能吸引学生的注意力,又能激发学生的学习兴趣。通过本课的学习,引导学生将所学知识与实际生活紧密联系,增强合作精神,培养学生数形结合能力和实践能力。
教学工具
导学案,硬纸板做成的圆柱,多媒体
教学方法
启发、诱导法.动手操作以及学生的互动合作相结合,利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题.
教学程序
教师活动
学生活动
设计意图
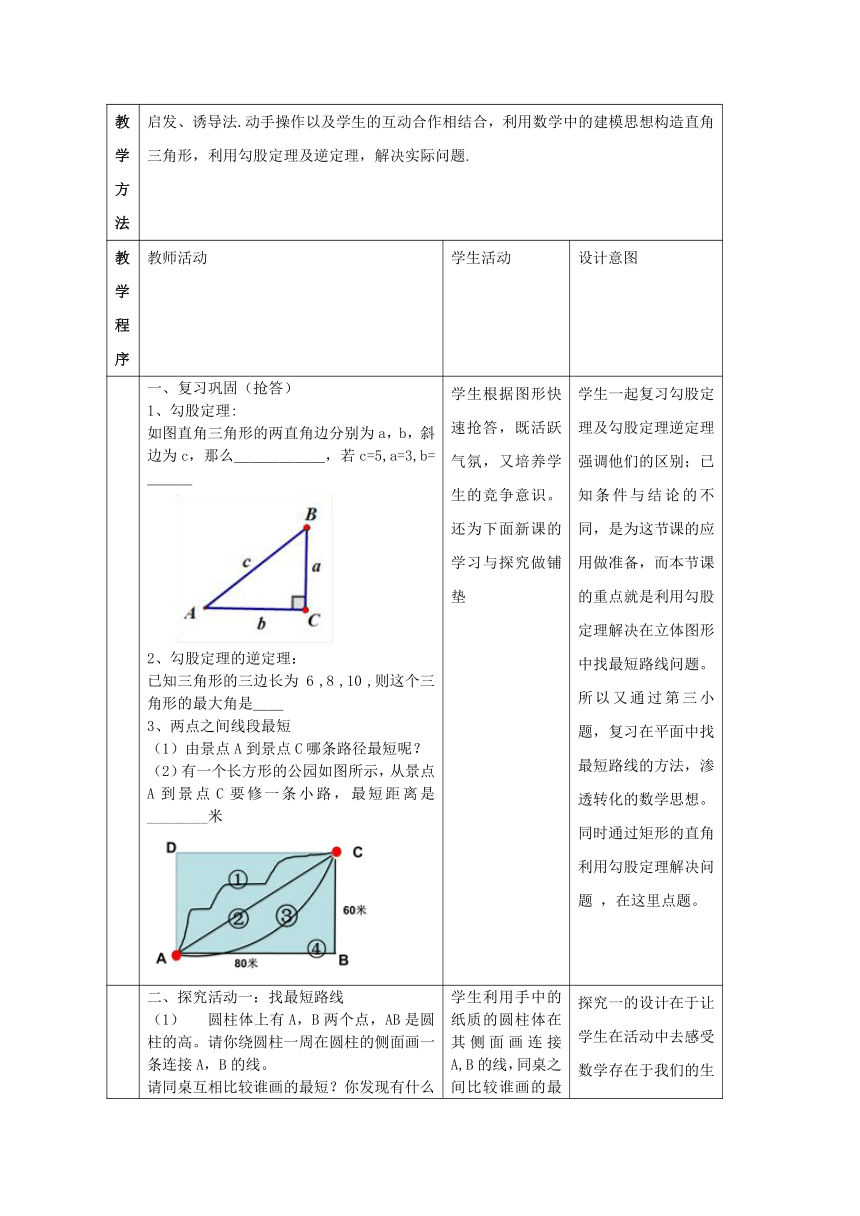
一、复习巩固????(抢答)1、勾股定理:
如图直角三角形的两直角边分别为a,b,斜边为c,那么______,若c=5,a=3,b=
___2、勾股定理的逆定理:已知三角形的三边长为
6
,8
,10
,则这个三角形的最大角是__3、两点之间线段最短(1)由景点A到景点C哪条路径最短呢?(2)有一个长方形的公园如图所示,从景点A到景点C要修一条小路,最短距离是________米
学生根据图形快速抢答,既活跃气氛,又培养学生的竞争意识。还为下面新课的学习与探究做铺垫
学生一起复习勾股定理及勾股定理逆定理强调他们的区别;已知条件与结论的不同,是为这节课的应用做准备,而本节课的重点就是利用勾股定理解决在立体图形中找最短路线问题。所以又通过第三小题,复面中找最短路线的方法,渗透转化的数学思想。同时通过矩形的直角利用勾股定理解决问题
,在这里点题。
二、探究活动一:找最短路线(1)
圆柱体上有A,B两个点,AB是圆柱的高。请你绕圆柱一周在圆柱的侧面画一条连接A,B的线。
请同桌互相比较谁画的最短?你发现有什么问题?思考:如何解决这个问题呢?小组交流BA
学生利用手中的纸质的圆柱体在其侧面画连接A,B的线,同桌之间比较谁画的最短,在比较时学生发现无法比较大小,原因在于线是曲线,在曲面上无法比较大小,从而发现问题。带着问题去交流探究如何转化成平面图形解决问题。小组交流后,找一个小组的代表画到黑板上的图形中,便于交流,比较。也为下面的总结做铺垫。
探究一的设计在于让学生在活动中去感受数学存在于我们的生活中,通过亲自动手操作发现问题,,体会到立体图形中找最短路线的困难,激发学生的学习兴趣
若CB是上底面的直径。点C和点A我们叫上下两底面的相对点。你能沿侧面画出连接A,C的最短的线吗?
第2问,学生利用解决第1问的做法再次画连接立体图形中最短路径。学生在黑板的展开图形画,感受点的位置不同,划线的区别。同时动画演示圆柱的侧面展开图中矩形的长,宽,与圆柱体的高,底面圆周长的关系。为下面用勾股定理解决问题做好准备这一问也让学生画在黑板上,便于教师总结时,对比说明问题。(总结完后,给学生2分钟时间理解消化)
这一问第一是为了让学生再次体会立体图形找最短路径要通过把圆柱的侧面展开成矩形,连接两点,通过“两点之间线段最短“确定。第二,是为了让学生体会点在立体图形的位置不同,那么在展开图中,两点的位置也不同,所以在画线时,首先应该确定好关键点的位置。第三.让学生明确圆柱的侧面展开成矩形后,矩形的长、宽与圆柱体的底面圆周长和高之间的关系
三、学以致用有一个圆柱体,它的高等于12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它沿圆柱的侧面爬行,想吃到上底面上与A点相对的B点处的蛋糕。最短路径是多少?
学生审题,自己讲解解决问题的方法,教师在黑板板演步骤,规范符号语言。起到示范的作用。同时教师强调细节,展开图的画法,做解答题的步骤。
学生在实际问题中,去利用刚才学会的在立体图形中找最短路径的方法解决蚂蚁吃蛋糕问题。体会利用勾股定理求最短路径的方法。渗透转化的数学思想。
应用定理解决问题时,感受勾股定理的奥妙。
四、巩固练习
如图,有一圆柱,它的高CD是10cm,底面半径是2cm,在圆柱的下底面A点处有一只小蚂蚁,它想吃到B点(BC=2cm)处的食物,需要爬行的最短距离是多少?
(取3)
学生在导纲上独立完成练习。教师同时可以辅导,查漏补缺。学生也可以互相帮助。一个学生在黑板板书,起到示范作用。
学生用符号语言演绎过程,规范学生的书写步骤。让学生上黑板板书步骤,以作示范。
五、探究活动二:勾股定理的逆运用李叔叔想要检测雕塑底座正面边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺。1、你能替他想办法完成任务?2、李叔叔量的AD是30cm,AB是40cm,BD是50cm,边AD垂直AB吗?3、若小明随身只有一个长度为20cm的刻度尺,他能有办法吗?
活动二,是勾股定理的逆运用。前两问,学生直接口答即可,一起交流。第3问,学生自己思考后,再小组交流想法。然后小组代表展示。
这一环节是勾股定理的逆定理的应用。学生做起来简单。做这个题是让学生再次的感受数学来源于生活,体会灵活应用数学知识解决实际问题的思想。
六、硕果飘香——小结你知道了什么知识?你体会了什么数学思想?你还有疑问吗?
先学生自己交流本节课的收获,然后起来共享
梳理知识及数学思想,及解题的方法。
九、布置作业作业:巩固性作业:课本p78,随堂1,2拓展性作业:必做:课本p78,习题2,3。选作:《伴》拓展提高
学生完成作业
通过作业反馈学生学习情况,体现分层次教学
《勾股定理的应用举例》教学设计
第一课时
教学目标
知识与能力:能运用勾股定理及直角三角形的判别条件(即勾股定理的逆定理)解决简单的实际问题.过程与方法:1.学会观察图形,勇于探索图形间的关系,培养学生的空间观念.2.在将实际问题抽象成几何图形过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.情感、态度、价值观:1.通过有趣的问题提高学习数学的兴趣.2.在解决实际问题的过程中,体验数学学习的实用性,体现人人都学有用的数学.
重难点
教学重点:探索、发现给定事物中隐含的勾股定理及其逆及理,并用它们解决生活实际问题.教学难点:利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题.
学情分析
本节位于七年级上册教材第三章第3节,在前面学习了应用勾股定理及勾股定理的逆定理的基础之上,围绕勾股定理及其逆定理,按照“问题情景—建立模型—解释—应用与拓展”的模式展开活动,,学生能够通过简单操作发现在圆柱侧面找最短路径方法,会利用勾股定理解决问题,初步感受应用勾股定理解决问题的思路,为后面探究它的应用做铺垫本节课的综合性和拓展性较强,教材图文并茂,既能吸引学生的注意力,又能激发学生的学习兴趣。通过本课的学习,引导学生将所学知识与实际生活紧密联系,增强合作精神,培养学生数形结合能力和实践能力。
教学工具
导学案,硬纸板做成的圆柱,多媒体
教学方法
启发、诱导法.动手操作以及学生的互动合作相结合,利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题.
教学程序
教师活动
学生活动
设计意图
一、复习巩固????(抢答)1、勾股定理:
如图直角三角形的两直角边分别为a,b,斜边为c,那么______,若c=5,a=3,b=
___2、勾股定理的逆定理:已知三角形的三边长为
6
,8
,10
,则这个三角形的最大角是__3、两点之间线段最短(1)由景点A到景点C哪条路径最短呢?(2)有一个长方形的公园如图所示,从景点A到景点C要修一条小路,最短距离是________米
学生根据图形快速抢答,既活跃气氛,又培养学生的竞争意识。还为下面新课的学习与探究做铺垫
学生一起复习勾股定理及勾股定理逆定理强调他们的区别;已知条件与结论的不同,是为这节课的应用做准备,而本节课的重点就是利用勾股定理解决在立体图形中找最短路线问题。所以又通过第三小题,复面中找最短路线的方法,渗透转化的数学思想。同时通过矩形的直角利用勾股定理解决问题
,在这里点题。
二、探究活动一:找最短路线(1)
圆柱体上有A,B两个点,AB是圆柱的高。请你绕圆柱一周在圆柱的侧面画一条连接A,B的线。
请同桌互相比较谁画的最短?你发现有什么问题?思考:如何解决这个问题呢?小组交流BA
学生利用手中的纸质的圆柱体在其侧面画连接A,B的线,同桌之间比较谁画的最短,在比较时学生发现无法比较大小,原因在于线是曲线,在曲面上无法比较大小,从而发现问题。带着问题去交流探究如何转化成平面图形解决问题。小组交流后,找一个小组的代表画到黑板上的图形中,便于交流,比较。也为下面的总结做铺垫。
探究一的设计在于让学生在活动中去感受数学存在于我们的生活中,通过亲自动手操作发现问题,,体会到立体图形中找最短路线的困难,激发学生的学习兴趣
若CB是上底面的直径。点C和点A我们叫上下两底面的相对点。你能沿侧面画出连接A,C的最短的线吗?
第2问,学生利用解决第1问的做法再次画连接立体图形中最短路径。学生在黑板的展开图形画,感受点的位置不同,划线的区别。同时动画演示圆柱的侧面展开图中矩形的长,宽,与圆柱体的高,底面圆周长的关系。为下面用勾股定理解决问题做好准备这一问也让学生画在黑板上,便于教师总结时,对比说明问题。(总结完后,给学生2分钟时间理解消化)
这一问第一是为了让学生再次体会立体图形找最短路径要通过把圆柱的侧面展开成矩形,连接两点,通过“两点之间线段最短“确定。第二,是为了让学生体会点在立体图形的位置不同,那么在展开图中,两点的位置也不同,所以在画线时,首先应该确定好关键点的位置。第三.让学生明确圆柱的侧面展开成矩形后,矩形的长、宽与圆柱体的底面圆周长和高之间的关系
三、学以致用有一个圆柱体,它的高等于12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它沿圆柱的侧面爬行,想吃到上底面上与A点相对的B点处的蛋糕。最短路径是多少?
学生审题,自己讲解解决问题的方法,教师在黑板板演步骤,规范符号语言。起到示范的作用。同时教师强调细节,展开图的画法,做解答题的步骤。
学生在实际问题中,去利用刚才学会的在立体图形中找最短路径的方法解决蚂蚁吃蛋糕问题。体会利用勾股定理求最短路径的方法。渗透转化的数学思想。
应用定理解决问题时,感受勾股定理的奥妙。
四、巩固练习
如图,有一圆柱,它的高CD是10cm,底面半径是2cm,在圆柱的下底面A点处有一只小蚂蚁,它想吃到B点(BC=2cm)处的食物,需要爬行的最短距离是多少?
(取3)
学生在导纲上独立完成练习。教师同时可以辅导,查漏补缺。学生也可以互相帮助。一个学生在黑板板书,起到示范作用。
学生用符号语言演绎过程,规范学生的书写步骤。让学生上黑板板书步骤,以作示范。
五、探究活动二:勾股定理的逆运用李叔叔想要检测雕塑底座正面边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺。1、你能替他想办法完成任务?2、李叔叔量的AD是30cm,AB是40cm,BD是50cm,边AD垂直AB吗?3、若小明随身只有一个长度为20cm的刻度尺,他能有办法吗?
活动二,是勾股定理的逆运用。前两问,学生直接口答即可,一起交流。第3问,学生自己思考后,再小组交流想法。然后小组代表展示。
这一环节是勾股定理的逆定理的应用。学生做起来简单。做这个题是让学生再次的感受数学来源于生活,体会灵活应用数学知识解决实际问题的思想。
六、硕果飘香——小结你知道了什么知识?你体会了什么数学思想?你还有疑问吗?
先学生自己交流本节课的收获,然后起来共享
梳理知识及数学思想,及解题的方法。
九、布置作业作业:巩固性作业:课本p78,随堂1,2拓展性作业:必做:课本p78,习题2,3。选作:《伴》拓展提高
学生完成作业
通过作业反馈学生学习情况,体现分层次教学
