鲁教版(五四制)七上3.3勾股定理的应用举例 教案(表格式)
文档属性
| 名称 | 鲁教版(五四制)七上3.3勾股定理的应用举例 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-30 00:00:00 | ||
图片预览

文档简介
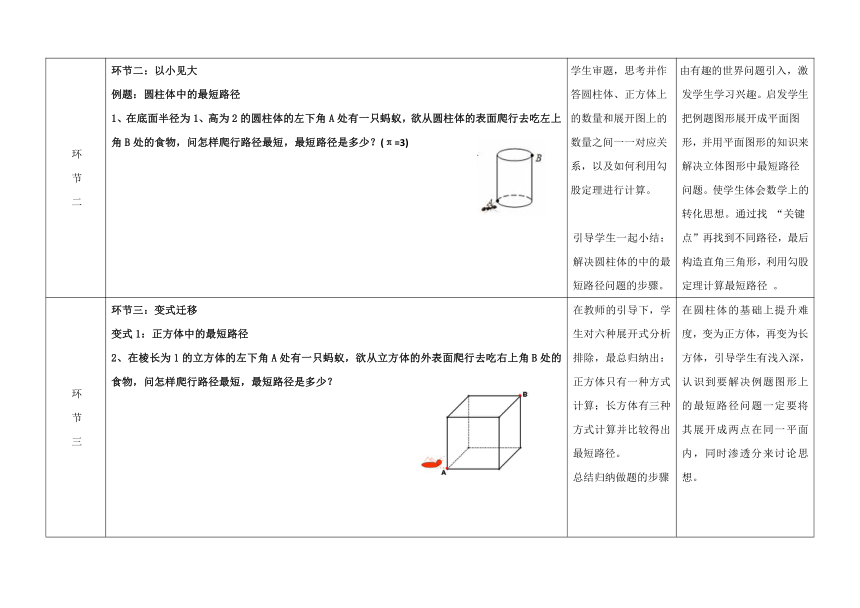
勾股定理的应用举例——立体图形中最短路径问题
1、教学目标:
1、
能运用勾股定理求最短路径问题。
2、
通过将实际问题抽象成几何图形过程中,提高学生分析问题、解决问题的能力,渗透数学建模思想,同时使学生体会转化和分类讨论的思想。
2、教学重、难点:
重点:探索、发现立体图形展开成平面图形的各种途径,利用勾股定理求最短路径问题。
难点:利用数学中的建模思想构造直角三角形,寻找不同路径,利用勾股定理解决实际问题。
3、教学过程:
环节
教学活动过程设计
设计意图
教学内容及教师活动
学生活动
环节一
环节一:以退为进1、一只蚂蚁想从一扇矩形窗户的左下角A点处爬到右上角D点处吃食物,请你帮它选择一条最近的路线(
)A、①B、②C、③
回顾勾股定理和两点之间线段最短的知识。
帮助学生温故知新,为学习本节内容铺垫。
环节二
环节二:以小见大例题:圆柱体中的最短路径1、在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁,欲从圆柱体的表面爬行去吃左上角B处的食物,问怎样爬行路径最短,最短路径是多少?(π=3)
学生审题,思考并作答圆柱体、正方体上的数量和展开图上的数量之间一一对应关系,以及如何利用勾股定理进行计算。引导学生一起小结:解决圆柱体的中的最短路径问题的步骤。
由有趣的世界问题引入,激发学生学习兴趣。启发学生把例题图形展开成平面图形,并用平面图形的知识来解决立体图形中最短路径问题。使学生体会数学上的转化思想。通过找
“关键点”再找到不同路径,最后构造直角三角形,利用勾股定理计算最短路径
。
环节三
环节三:变式迁移变式1:正方体中的最短路径2、在棱长为1的立方体的左下角A处有一只蚂蚁,欲从立方体的外表面爬行去吃右上角B处的食物,问怎样爬行路径最短,最短路径是多少?
变式2:长方体中的最短路径3、在长为4、宽为2、高为1的实心长方体的右下角A处有一只蚂蚁想从长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
在教师的引导下,学生对六种展开式分析排除,最总归纳出:正方体只有一种方式计算;长方体有三种方式计算并比较得出最短路径。总结归纳做题的步骤
在圆柱体的基础上提升难度,变为正方体,再变为长方体,引导学生有浅入深,认识到要解决例题图形上的最短路径问题一定要将其展开成两点在同一平面内,同时渗透分来讨论思想。
环节四
环节四:技能训练1、有一圆形油罐底面圆的周长为16m,高为7m,一只蚂蚁从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?2、如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
教师布置任务,学生按照要求完成任务。教师训堂,并适时对学生的解答以及出现的问题进行点拨。
通过巩固练习,加深学生对本节课所学知识的印象和理解,提高课堂的有效性。
环节五
环节五:拓展训练
3、如图:圆柱形玻璃杯,高为12cm,底面圆的周长为18cm,在杯子内壁离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯子外壁,距离杯子上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为多少?
供学有余力的同学使用
把曲线化为直线,将此问题转化为利用轴对称解决最短路径问题,将寻找最短路径问题提升到求最短路径长,体现勾股定理是计算线段长的有力手段。
环节六
环节六:小结解决立体图形最短路径问题的步骤:展(立体展成平面)找(找起点,终点)连(连各种路径)算(用勾股定理算各种路径的长度)答
根据板书进行小结
1、教学目标:
1、
能运用勾股定理求最短路径问题。
2、
通过将实际问题抽象成几何图形过程中,提高学生分析问题、解决问题的能力,渗透数学建模思想,同时使学生体会转化和分类讨论的思想。
2、教学重、难点:
重点:探索、发现立体图形展开成平面图形的各种途径,利用勾股定理求最短路径问题。
难点:利用数学中的建模思想构造直角三角形,寻找不同路径,利用勾股定理解决实际问题。
3、教学过程:
环节
教学活动过程设计
设计意图
教学内容及教师活动
学生活动
环节一
环节一:以退为进1、一只蚂蚁想从一扇矩形窗户的左下角A点处爬到右上角D点处吃食物,请你帮它选择一条最近的路线(
)A、①B、②C、③
回顾勾股定理和两点之间线段最短的知识。
帮助学生温故知新,为学习本节内容铺垫。
环节二
环节二:以小见大例题:圆柱体中的最短路径1、在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁,欲从圆柱体的表面爬行去吃左上角B处的食物,问怎样爬行路径最短,最短路径是多少?(π=3)
学生审题,思考并作答圆柱体、正方体上的数量和展开图上的数量之间一一对应关系,以及如何利用勾股定理进行计算。引导学生一起小结:解决圆柱体的中的最短路径问题的步骤。
由有趣的世界问题引入,激发学生学习兴趣。启发学生把例题图形展开成平面图形,并用平面图形的知识来解决立体图形中最短路径问题。使学生体会数学上的转化思想。通过找
“关键点”再找到不同路径,最后构造直角三角形,利用勾股定理计算最短路径
。
环节三
环节三:变式迁移变式1:正方体中的最短路径2、在棱长为1的立方体的左下角A处有一只蚂蚁,欲从立方体的外表面爬行去吃右上角B处的食物,问怎样爬行路径最短,最短路径是多少?
变式2:长方体中的最短路径3、在长为4、宽为2、高为1的实心长方体的右下角A处有一只蚂蚁想从长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
在教师的引导下,学生对六种展开式分析排除,最总归纳出:正方体只有一种方式计算;长方体有三种方式计算并比较得出最短路径。总结归纳做题的步骤
在圆柱体的基础上提升难度,变为正方体,再变为长方体,引导学生有浅入深,认识到要解决例题图形上的最短路径问题一定要将其展开成两点在同一平面内,同时渗透分来讨论思想。
环节四
环节四:技能训练1、有一圆形油罐底面圆的周长为16m,高为7m,一只蚂蚁从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?2、如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
教师布置任务,学生按照要求完成任务。教师训堂,并适时对学生的解答以及出现的问题进行点拨。
通过巩固练习,加深学生对本节课所学知识的印象和理解,提高课堂的有效性。
环节五
环节五:拓展训练
3、如图:圆柱形玻璃杯,高为12cm,底面圆的周长为18cm,在杯子内壁离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯子外壁,距离杯子上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为多少?
供学有余力的同学使用
把曲线化为直线,将此问题转化为利用轴对称解决最短路径问题,将寻找最短路径问题提升到求最短路径长,体现勾股定理是计算线段长的有力手段。
环节六
环节六:小结解决立体图形最短路径问题的步骤:展(立体展成平面)找(找起点,终点)连(连各种路径)算(用勾股定理算各种路径的长度)答
根据板书进行小结
