4.2视图-2021-2022学年数学鲁教版九年级上册同步课时作业(Word版含答案)
文档属性
| 名称 | 4.2视图-2021-2022学年数学鲁教版九年级上册同步课时作业(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 166.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 10:12:42 | ||
图片预览

文档简介
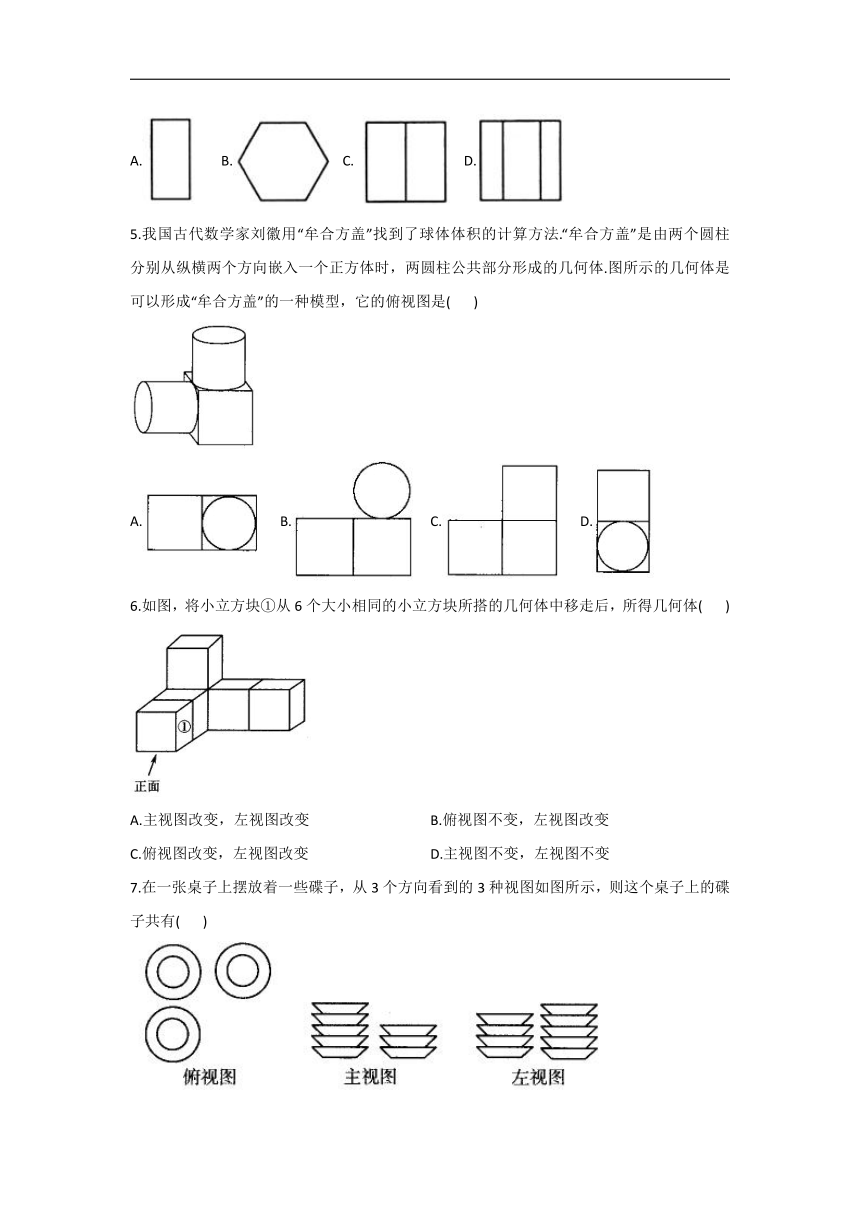
4.2视图—2021-2022学年数学鲁教版九年级上册同步课时作业
1.下图是某几何体的三视图,该几何体是(
)
A.圆柱
B.圆锥
C.三棱柱
D.长方体
2.下面四个几何体中,主视图为三角形的是(
)
A.
B.
C.
D.
3.图是由手提水果篮抽象成的几何体,以箭头所指的方向为主视方向,则它的俯视图为(
)
A.
B.
C.
D.
4.如图,下列选项中不是正六棱柱的三视图的是(
)
A.
B.
C.
D.
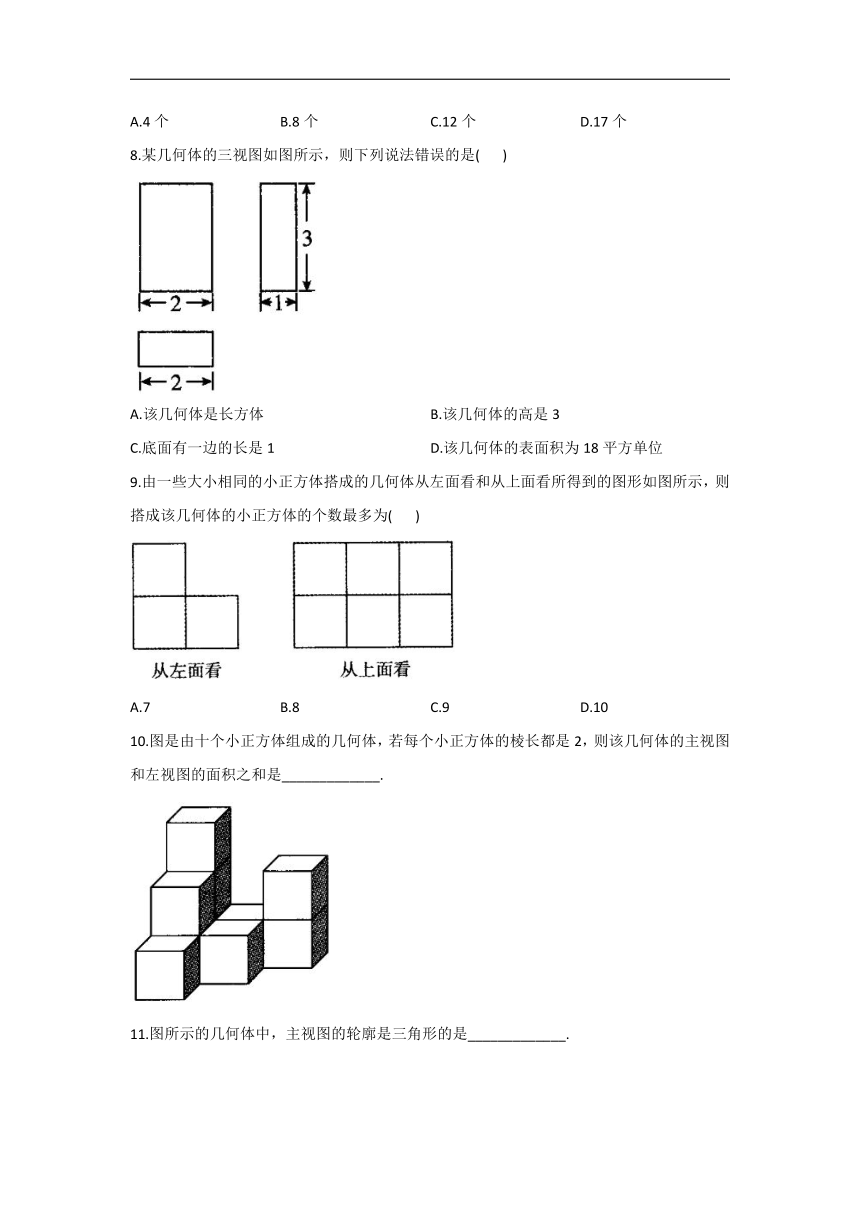
5.我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时,两圆柱公共部分形成的几何体.图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是(
)
A.
B.
C.
D.
6.如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图改变
C.俯视图改变,左视图改变
D.主视图不变,左视图不变
7.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有(
)
A.4个
B.8个
C.12个
D.17个
8.某几何体的三视图如图所示,则下列说法错误的是(
)
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
9.由一些大小相同的小正方体搭成的几何体从左面看和从上面看所得到的图形如图所示,则搭成该几何体的小正方体的个数最多为(
)
A.7
B.8
C.9
D.10
10.图是由十个小正方体组成的几何体,若每个小正方体的棱长都是2,则该几何体的主视图和左视图的面积之和是_____________.
11.图所示的几何体中,主视图的轮廓是三角形的是_____________.
12.一个圆柱的三视图如图所示,则这个圆柱的体积为_____________.
13.由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置上的小正方体个数.
(1)请在图中画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为__________;
(3)在不改变主视图和俯视图的情况下,最多可添加________个小正方体.
答案以及解析
1.答案:D
解析:本题考查由三视图判断几何体.由三视图可知,该几何体的主视图、左视图、俯视图都是长方形,故该几何体是长方体,故选D.
2.答案:B
解析:题中四个几何体的主视图依次为圆,三角形,矩形,正方形.故选B.
3.答案:A
解析:水果篮下面篮子的俯视图是圆,上面提手的俯视图是线段,且用实线表示.故选A.
4.答案:A
解析:如题图放置的正六棱柱的三视图分别为主视图:三个左右相邻的矩形,左视图:两个左右相邻的矩形,俯视图:正六边形.故选A.
5.答案:A
解析:横向圆柱的俯视图是正方形,纵向圆柱的俯视图是圆,正方体的俯视图是正方形,结合题图可知几何体俯视图中两正方形横向并排,且圆在右侧正方形内.故选A.
6.答案:C
解析:本题考查简单几何体的三视图.移动小立方块①,所得的几何体的主视图没有改变,左视图、俯视图发生变化,故选C.
7.答案:C
解析:本题考查由三视图判断几何体从俯视图可知该桌子共摆放着三摞碟子;从主视图可知左侧碟子有5个,右侧有3个;从左视图可知左侧碟子有4个,右侧与主视图的左侧碟子个数相同,所以共计有12个碟子,故选C.
8.答案:D
解析:本题考查几何体的三视图.根据已知几何体的三视图,可判断此几何体是长方体,∴选项A正确;根据左视图中标明的数据,可知几何体的高是3,∴选项B正确;根据左视图中标明的数据,可知几何体的底边一边长为1,∴选项C正确;该几何体的表面积为选项D错误,故选D.
9.答案:C
解析:由从上面看所得到的图形易得最底层有6个小正方体,第二层最多有3个小正方体,所以搭成这个几何体的小正方体最多为(个).故选C.
10.答案:48
解析:该几何体的主视图和左视图如下,面积之和为.
11.答案:②③
解析:①的主视图的轮廓是矩形;②的主视图的轮廓是三角形,③的主视图的轮廓是等腰三角形,故答案是②③.
12.答案:24π
解析:由三视图可得该圆柱的高为6,底面直径为4,则这个圆柱的体积为.
13.答案:(1)该几何体的主视图和左视图如图所示.
(2)32.
给这个几何体喷上颜色(底面不喷色),需要喷色的面有32个,所以喷色的面积为32.
(3)1.
在俯视图中标数字“2”的正方形的位置上再添加1个小正方体,不会改变主视图和俯视图.
1.下图是某几何体的三视图,该几何体是(
)
A.圆柱
B.圆锥
C.三棱柱
D.长方体
2.下面四个几何体中,主视图为三角形的是(
)
A.
B.
C.
D.
3.图是由手提水果篮抽象成的几何体,以箭头所指的方向为主视方向,则它的俯视图为(
)
A.
B.
C.
D.
4.如图,下列选项中不是正六棱柱的三视图的是(
)
A.
B.
C.
D.
5.我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时,两圆柱公共部分形成的几何体.图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是(
)
A.
B.
C.
D.
6.如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体(
)
A.主视图改变,左视图改变
B.俯视图不变,左视图改变
C.俯视图改变,左视图改变
D.主视图不变,左视图不变
7.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有(
)
A.4个
B.8个
C.12个
D.17个
8.某几何体的三视图如图所示,则下列说法错误的是(
)
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
9.由一些大小相同的小正方体搭成的几何体从左面看和从上面看所得到的图形如图所示,则搭成该几何体的小正方体的个数最多为(
)
A.7
B.8
C.9
D.10
10.图是由十个小正方体组成的几何体,若每个小正方体的棱长都是2,则该几何体的主视图和左视图的面积之和是_____________.
11.图所示的几何体中,主视图的轮廓是三角形的是_____________.
12.一个圆柱的三视图如图所示,则这个圆柱的体积为_____________.
13.由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置上的小正方体个数.
(1)请在图中画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为__________;
(3)在不改变主视图和俯视图的情况下,最多可添加________个小正方体.
答案以及解析
1.答案:D
解析:本题考查由三视图判断几何体.由三视图可知,该几何体的主视图、左视图、俯视图都是长方形,故该几何体是长方体,故选D.
2.答案:B
解析:题中四个几何体的主视图依次为圆,三角形,矩形,正方形.故选B.
3.答案:A
解析:水果篮下面篮子的俯视图是圆,上面提手的俯视图是线段,且用实线表示.故选A.
4.答案:A
解析:如题图放置的正六棱柱的三视图分别为主视图:三个左右相邻的矩形,左视图:两个左右相邻的矩形,俯视图:正六边形.故选A.
5.答案:A
解析:横向圆柱的俯视图是正方形,纵向圆柱的俯视图是圆,正方体的俯视图是正方形,结合题图可知几何体俯视图中两正方形横向并排,且圆在右侧正方形内.故选A.
6.答案:C
解析:本题考查简单几何体的三视图.移动小立方块①,所得的几何体的主视图没有改变,左视图、俯视图发生变化,故选C.
7.答案:C
解析:本题考查由三视图判断几何体从俯视图可知该桌子共摆放着三摞碟子;从主视图可知左侧碟子有5个,右侧有3个;从左视图可知左侧碟子有4个,右侧与主视图的左侧碟子个数相同,所以共计有12个碟子,故选C.
8.答案:D
解析:本题考查几何体的三视图.根据已知几何体的三视图,可判断此几何体是长方体,∴选项A正确;根据左视图中标明的数据,可知几何体的高是3,∴选项B正确;根据左视图中标明的数据,可知几何体的底边一边长为1,∴选项C正确;该几何体的表面积为选项D错误,故选D.
9.答案:C
解析:由从上面看所得到的图形易得最底层有6个小正方体,第二层最多有3个小正方体,所以搭成这个几何体的小正方体最多为(个).故选C.
10.答案:48
解析:该几何体的主视图和左视图如下,面积之和为.
11.答案:②③
解析:①的主视图的轮廓是矩形;②的主视图的轮廓是三角形,③的主视图的轮廓是等腰三角形,故答案是②③.
12.答案:24π
解析:由三视图可得该圆柱的高为6,底面直径为4,则这个圆柱的体积为.
13.答案:(1)该几何体的主视图和左视图如图所示.
(2)32.
给这个几何体喷上颜色(底面不喷色),需要喷色的面有32个,所以喷色的面积为32.
(3)1.
在俯视图中标数字“2”的正方形的位置上再添加1个小正方体,不会改变主视图和俯视图.
