3.7二次函数与一元二次方程-2021-2022学年数学鲁教版九年级上册同步课时作业(Word版 含答案)
文档属性
| 名称 | 3.7二次函数与一元二次方程-2021-2022学年数学鲁教版九年级上册同步课时作业(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 328.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览


文档简介
3.7二次函数与一元二次方程—2021-2022学年数学鲁教版九年级上册同步课时作业
1.如图,点,在二次函数的图象上,则方程的一个近似值可能是(
)
A.2.18
B.2.68
C.
D.2.45
2.下列各点是抛物线与x轴的交点的为(
)
A.点
B.点
C.点
D.点
3.已知二次函数的图像与x轴有交点,则m的取值范围是(
)
A.
B.
C.
D.
4.下表是二次函数的自变量与函数值(精确到0.01)的部分对应值,据此判断方程(,为常数)的一个根所在的范围是(
)
6.17
6.18
6.19
6.20
0.02
0.06
A.
B.
C.
D.
5.二次函数(,为常数)的图象如图所示,设关于的一元二次方程的两个实数根分别为,若,则实数的取值范围是(
)
A.
B.
C.
D.
6.若二次函数图象的对称轴是直线,则关于x的方程的解为(
)
A.
B.
C.
D.
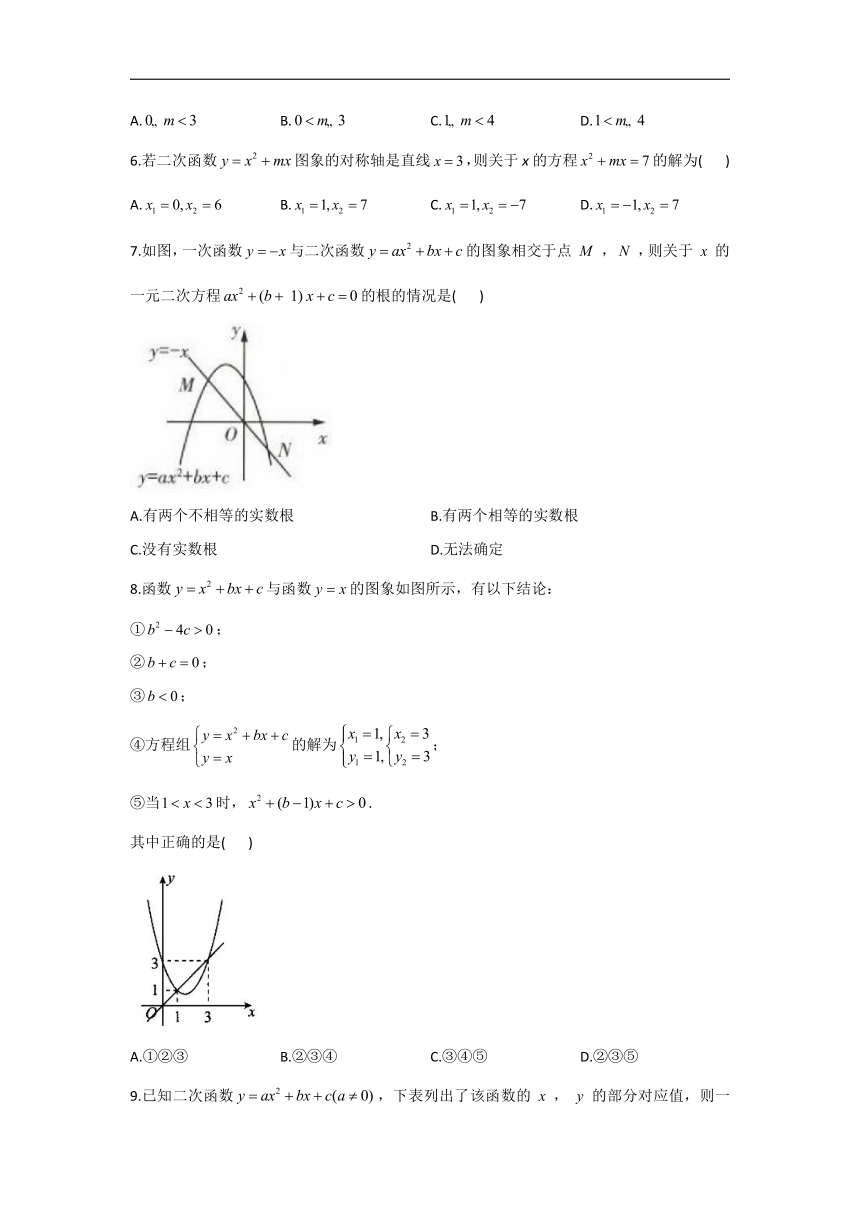
7.如图,一次函数与二次函数的图象相交于点,,则关于的一元二次方程的根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
8.函数与函数的图象如图所示,有以下结论:
①;
②;
③;
④方程组的解为;
⑤当时,.
其中正确的是(
)
A.①②③
B.②③④
C.③④⑤
D.②③⑤
9.已知二次函数,下表列出了该函数的,的部分对应值,则一元二次方程的根是(
)
…
0
1
2
3
…
…
4
5
4
2
…
A.
B.
C.
D.
10.二次函数的图像与x轴的交点坐标是__________.
11.已知函数中,函数值与自变量的部分对应值如下表:
x
…
2.41
2.54
2.67
2.75
…
y
…
-0.43
-0.17
0.12
0.32
…
则方程的一个解的范围为__________.
12.若抛物线与x轴没有交点,则m的取值范围是_____________.
13.利用二次函数的图象求一元二次方程的近似根.
答案以及解析
1.答案:D
解析:图象上有两点分别为当时,;当时,,当时,.只有选项D符合.故选D.
2.答案:C
解析:令,可得,即抛物线与x轴的交点分别为点.故选C.
3.答案:A
解析:二次函数的图像与x轴有交点,,解得.故选A.
4.答案:C
解析:由题中表格中数据可得当时,,当时,,由此可得方程的一个根所在的范围是.故选C.
5.答案:D
解析:一元二次方程可变形为,由题意,得抛物线与直线的两个交点的横坐标同号,所以,解得.故选D.
6.答案:D
解析:因为二次函数图象的对称轴是直线,所以,解得.关于x的方程,即,解得.故选D.
7.答案:A
解析:一次函数与二次函数的图象有两个交点,关于的一元二次方程有两个不相等的实数根,有两个不相等的实数根.故选A.
8.答案:B
解析:①抛物线与x轴没有交点,,①不正确;②函数的图象经过点,②正确;③抛物线的对称轴在y轴右侧,.③正确;④函数与函数的图象交于点方程组的解为,④正确;⑤由图象知,当时,,即,⑤不正确.
9.答案:D
解析:一元二次方程的根是抛物线与直线的交点的横坐标.由题中表格,可知抛物线与直线的一个交点为,因为当和时,函数值都是4,所以抛物线的对称轴是直线,根据抛物线的对称性,可知抛物线与直线的另一个交点坐标为,所以一元二次方程的根是.故选D.
10.答案:
解析:当时,,解得,所以二次函数的图像与x轴的交点坐标是.
11.答案:
解析:由表格中的数据看出-0.17和0.12更接近于0,方程的一个解的范围是.
12.答案:
解析:抛物线与x轴没有交点,当时,,,解得.
13.答案:解:画出的图象,如图,由图象可知方程有两个根,一个根在-1和-2之间,另一个根在0和1之间.先求-1和-2之间的根,用计算器进行探索,
x
-1.1
-1.2
-1.3
-1.4
y
-0.35
0.4
1.25
2.2
因此,是方程的一个近似根.
另一个根可以类似地求出.
x
0.1
0.2
0.3
0.4
y
-1.55
-1
-0.35
0.4
因此是方程的另一个近似根.
1.如图,点,在二次函数的图象上,则方程的一个近似值可能是(
)
A.2.18
B.2.68
C.
D.2.45
2.下列各点是抛物线与x轴的交点的为(
)
A.点
B.点
C.点
D.点
3.已知二次函数的图像与x轴有交点,则m的取值范围是(
)
A.
B.
C.
D.
4.下表是二次函数的自变量与函数值(精确到0.01)的部分对应值,据此判断方程(,为常数)的一个根所在的范围是(
)
6.17
6.18
6.19
6.20
0.02
0.06
A.
B.
C.
D.
5.二次函数(,为常数)的图象如图所示,设关于的一元二次方程的两个实数根分别为,若,则实数的取值范围是(
)
A.
B.
C.
D.
6.若二次函数图象的对称轴是直线,则关于x的方程的解为(
)
A.
B.
C.
D.
7.如图,一次函数与二次函数的图象相交于点,,则关于的一元二次方程的根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
8.函数与函数的图象如图所示,有以下结论:
①;
②;
③;
④方程组的解为;
⑤当时,.
其中正确的是(
)
A.①②③
B.②③④
C.③④⑤
D.②③⑤
9.已知二次函数,下表列出了该函数的,的部分对应值,则一元二次方程的根是(
)
…
0
1
2
3
…
…
4
5
4
2
…
A.
B.
C.
D.
10.二次函数的图像与x轴的交点坐标是__________.
11.已知函数中,函数值与自变量的部分对应值如下表:
x
…
2.41
2.54
2.67
2.75
…
y
…
-0.43
-0.17
0.12
0.32
…
则方程的一个解的范围为__________.
12.若抛物线与x轴没有交点,则m的取值范围是_____________.
13.利用二次函数的图象求一元二次方程的近似根.
答案以及解析
1.答案:D
解析:图象上有两点分别为当时,;当时,,当时,.只有选项D符合.故选D.
2.答案:C
解析:令,可得,即抛物线与x轴的交点分别为点.故选C.
3.答案:A
解析:二次函数的图像与x轴有交点,,解得.故选A.
4.答案:C
解析:由题中表格中数据可得当时,,当时,,由此可得方程的一个根所在的范围是.故选C.
5.答案:D
解析:一元二次方程可变形为,由题意,得抛物线与直线的两个交点的横坐标同号,所以,解得.故选D.
6.答案:D
解析:因为二次函数图象的对称轴是直线,所以,解得.关于x的方程,即,解得.故选D.
7.答案:A
解析:一次函数与二次函数的图象有两个交点,关于的一元二次方程有两个不相等的实数根,有两个不相等的实数根.故选A.
8.答案:B
解析:①抛物线与x轴没有交点,,①不正确;②函数的图象经过点,②正确;③抛物线的对称轴在y轴右侧,.③正确;④函数与函数的图象交于点方程组的解为,④正确;⑤由图象知,当时,,即,⑤不正确.
9.答案:D
解析:一元二次方程的根是抛物线与直线的交点的横坐标.由题中表格,可知抛物线与直线的一个交点为,因为当和时,函数值都是4,所以抛物线的对称轴是直线,根据抛物线的对称性,可知抛物线与直线的另一个交点坐标为,所以一元二次方程的根是.故选D.
10.答案:
解析:当时,,解得,所以二次函数的图像与x轴的交点坐标是.
11.答案:
解析:由表格中的数据看出-0.17和0.12更接近于0,方程的一个解的范围是.
12.答案:
解析:抛物线与x轴没有交点,当时,,,解得.
13.答案:解:画出的图象,如图,由图象可知方程有两个根,一个根在-1和-2之间,另一个根在0和1之间.先求-1和-2之间的根,用计算器进行探索,
x
-1.1
-1.2
-1.3
-1.4
y
-0.35
0.4
1.25
2.2
因此,是方程的一个近似根.
另一个根可以类似地求出.
x
0.1
0.2
0.3
0.4
y
-1.55
-1
-0.35
0.4
因此是方程的另一个近似根.
