4.6角课后练习2020-2021学年 华东师大版七年级上册数学 (Word版 含答案)
文档属性
| 名称 | 4.6角课后练习2020-2021学年 华东师大版七年级上册数学 (Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 114.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览




文档简介
第四章图形的初步认识4.6角课后练习2020-2021学年上学期七年级上册初中数学华师大版
一、单选题(共12题
)
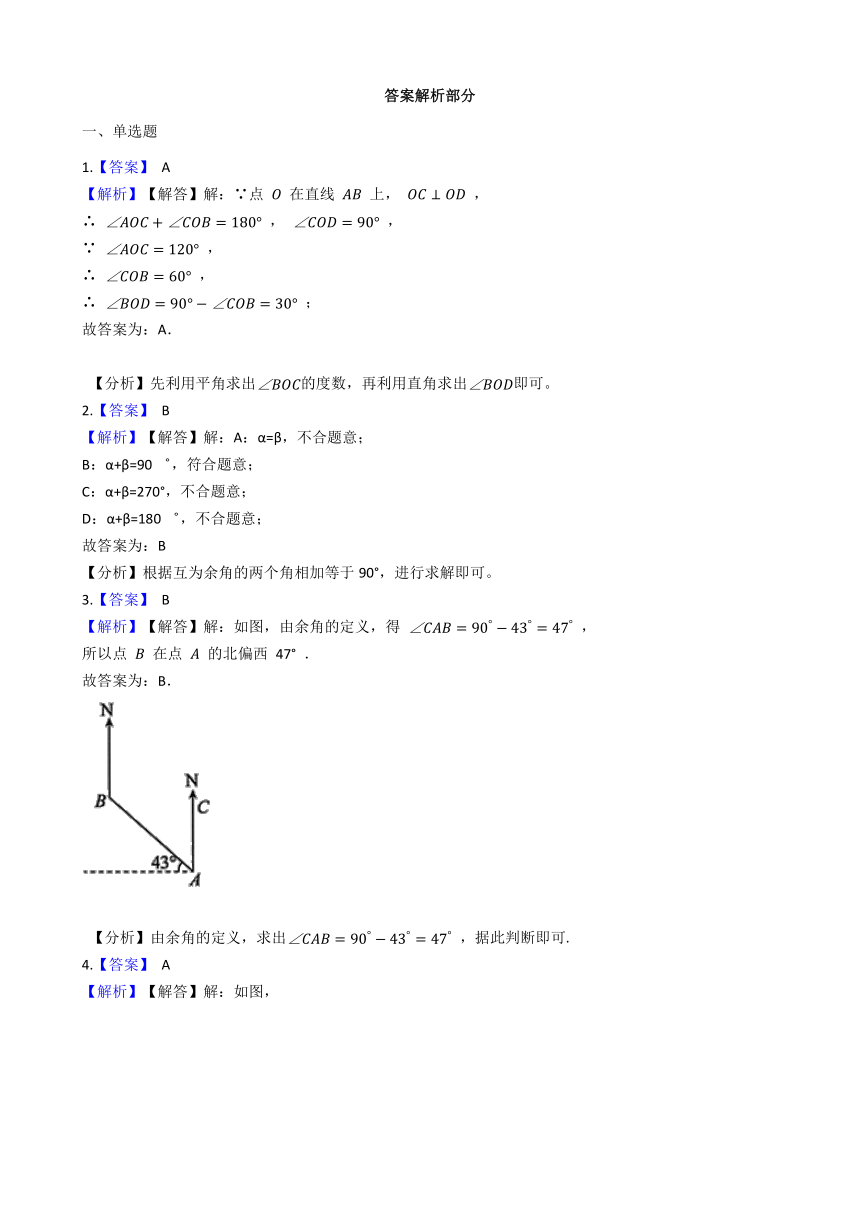
1.如图,点
在直线
上,
.若
,则
的大小为(
???)
A.????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
2.如图,将一副三角板按不同位置摆放,其中α和β互为余角的是( )
A.??????B.??????C.??????D.?
3.如图,点
相对于点
的方向是(???
)
A.?南偏东
????????????????????????B.?北偏西
47°????????????????????????C.?西偏北
47°????????????????????????D.?东偏南
47°
4.如图,有
三个地点,且
,从A地测得B地的方位角是北偏东
,那么从C地测B地的方位角是(???
)
A.?南偏东
?????????????????????B.?南偏西
?????????????????????C.?北偏东
?????????????????????D.?北偏西
5.如图,OA⊥OB,若∠1=55°16′,则∠2的度数是(??
)
A.?35°44′????????????????????????????????B.?34°84′????????????????????????????????C.?34°74′????????????????????????????????D.?34°44′
6.下列说法错误的是(??
)
A.?两个互余的角都是锐角
B.?锐角的补角大于这个角本身
C.?互为补角的两个角不可能都是锐角
D.?锐角大于它的余角
7.如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
8.
的余角是
,那么
的大小是(???
)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
9.一个角的余角是它的补角的
,这个角是(??
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
10.北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,過极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道
在点O南偏东70°的方向上,则这条跑道所在射线
与正北方向所成角的度数为( )
A.?160°?????????????????????????????????????B.?110°?????????????????????????????????????C.?70°?????????????????????????????????????D.?20°
11.如图,将一副直角三角尺叠放在一起,使直角顶点重合于点O,则下列说法一定成立的是(??
)
A.?
B.?
C.?
与
互补
D.?
与
互余
12.如图所示,点B在点O的北偏东60°,射线
与射线
所成的角是110°,则射线
的方向是(??
)
A.?北偏西30°?????????????????????????B.?北偏西40°?????????????????????????C.?西偏北50°?????????????????????????D.?北偏西50°
二、填空题(共6题
)
13.若两个角的两边两两互相平行,且一个角的
等于另一个角的
,则这两个角的度数分别为________度,________度
14.钟表在7点50分时,时针和分针所成的角是________.
15.
________°.
16.如果一个角的补角是120°,那么这个角的余角的度数是________.
17.已知
,则它的余角与补角的度数和等于________
.
18.若
,则α的补角
________.(用“度、分”表示).
三、综合题(共4题
)
19.已知一个角的余角比这个角的补角的一半还少
,求这个角及它的余角
用方程做
.
20.如图,
和
都是直角,若
,求
的度数.
21.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
22.如图,有甲、乙、丙、丁四个小岛,甲、乙、丙在同一条直线上,而且乙、丙在甲的正东方,丁岛在丙岛的正北方,甲岛在丁岛的南偏西52°方向,乙岛在丁岛的南偏东40°方向.那么,丁岛分别在甲岛和乙岛的什么方向?
答案解析部分
一、单选题
1.【答案】
A
【解析】【解答】解:∵点
在直线
上,
,
∴
,
,
∵
,
∴
,
∴
;
故答案为:A.
【分析】先利用平角求出的度数,再利用直角求出即可。
2.【答案】
B
【解析】【解答】解:A:α=β,不合题意;
B:α+β=90゜,符合题意;
C:α+β=270°,不合题意;
D:α+β=180゜,不合题意;
故答案为:B
【分析】根据互为余角的两个角相加等于90°,进行求解即可。
3.【答案】
B
【解析】【解答】解:如图,由余角的定义,得
,
所以点
在点
的北偏西
47°
.
故答案为:B.
【分析】由余角的定义,求出
,据此判断即可.
4.【答案】
A
【解析】【解答】解:如图,
∵AF//DE
,
∴∠ABE=∠FAB=43°,
∵AB⊥BC
,
∴∠ABC=90°,
∴∠CBD=47°,
∴C地在B地的北偏西47°的方向上.
∴从C地测B地的方位角是南偏东
故答案为:A
.
【分析】根据方向角的概念和平行线的性质求解,即可得出从C地测得B地的方位角。
5.【答案】
D
【解析】【解答】解:∵OA⊥OB,若∠1=55°16′,
∴∠1+∠2=90°,
∴∠2=90°-55°16′=34°44′.
故答案为:D.
【分析】利用垂直的定义可证得∠1+∠2=90°,再代入∠1的度数,可求出∠2的度数.
6.【答案】
D
【解析】【解答】解:A、两角互余,和为90°,两角均为锐角,故A选项不符合题意;
B、两角互补,和为180°,从而锐角的补角必为钝角,故B选项不符合题意;
C、两角互补,和为180°,两锐角的和必小于180°,故C选项不符合题意;
D、两角互余,和为90°,从而锐角不一定大于它的余角,也可以小于或者等于它的余角,故D选项不符合题意.
故答案为:D.
【分析】互为余角的两个角的和等于90°,互为补角的两个角的和等于180°,据此逐一判断即可.
7.【答案】
B
【解析】【解答】解:时针超过20分所走的度数为20×0.5=10°,
分针与8点之间的夹角为4×30=120°,
∴此时时钟面上的时针与分针的夹角是120+10=130°.
故选:B.
【分析】此时时针超过8点,
分针指向4
,
根据每2个数字之间相隔30度和时针1分钟走0.5度可得夹角度数.
8.【答案】
D
【解析】【解答】解:
的余角是
,
,
故答案为:D.
【分析】利用余角的性质求解即可。
9.【答案】
A
【解析】【解答】解:设这个角的度数是x°,则
,
解得:x=30,即这个角的度数是30°,
故答案为:A.
【分析】根据
一个角的余角是它的补角的??
可得
,
再解方程即可。
10.【答案】
B
【解析】【解答】解:∵
在点O南偏东
的方向上,
∴射线
与正北方向所成角的度数为:180°-70°=110°,
故答案为:B.
【分析】根据方向角及邻补角的定义进行解答即可.
11.【答案】
C
【解析】【解答】∵∠AOD=90°-∠DOC,
∠BOC=90°-∠DOC,
∴∠AOD=∠BOC,
∴∠AOB=∠AOD
+∠BOD=∠AOD+90°
∠COD+90°,故A错误;
∠AOB=∠AOD
+∠COD+∠BOC=2∠AOD+∠COD
2∠COD,故B错误;
∠AOB=∠AOC+∠DOB-∠DOC=90°+90°-∠COD=180°-∠COD,
∴∠AOB+∠COD=180°,即∠AOB与∠COD互补,故C正确,D错误;
故答案为:C.
【分析】A、根据同角的余角相等得出∠AOD=∠BOC,从而得出∠AOB=∠AOD+90°,即可判断A错误;
B、利用∠AOB=∠AOD
+∠COD+∠BOC得出∠AOB=2∠AOD+∠COD,即可判断B错误;
CD、利用∠AOB=∠AOC+∠DOB-∠DOC得出∠AOB=180°-∠COD,得出∠AOB与∠COD互补,即可判断C正确,D错误.
12.【答案】
D
【解析】【解答】解:∵射线OC与射线OB所成的角是110°,
∴∠COB=110°,
∵点B在点O的北偏东60°,
∴射线OB与正北方向所成的角是60°
∴射线OC与正北方向所成的角是110°-60°=50°,
∴射线OC的方向是北偏西50°.
故答案为:D.
【分析】根据射线OB和射线OC所成的角是110°,可得∠COB的度数,再根据角的和差关系求解即可得出OC与正北方向所成的角,从而解决问题.
二、填空题
13.【答案】
72;108
【解析】【解答】解:设较小的角的度数为x,则较大的角的度数为x
根据题意可得,x+x=180°
解得,x=72°
∴x=×72°=108°
【分析】根据题意,如果两个角的两边互相平行,则这两个角相等或互补,根据题意列出方程求出答案即可。
14.【答案】
65°
【解析】【解答】解:
7点50分时
时针转动了50×0.5=25°,
则时针和8之间还有30°-25°=5°,
故时针和分针之间夹角为30°×2+5°=65°.
故答案为:65°.
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,找出时针一分钟转0.5°,分针一分钟转6°,所以时针和分针所成的角是30°×2+5°=65°.
15.【答案】
65.7225
【解析】【解答】解:
,
,
故答案为:65.7225.
【分析】利用度分秒之间的关系进行转化即可.
16.【答案】
30°
【解析】【解答】解:∵一个角的补角是120°,
∴这个角为:180°?120°=60°,
∴这个角的余角为:90°?60°=30°.
故答案为:30°.
【分析】和为90°的两个角互为余角,和为180°的两个角互为补角,根据定义即可解答.
17.【答案】
170
【解析】【解答】解:
,
根据互为补角的概念,得
的补角为:
,
根据互为余角的概念,得,
的余角为:
,
余角与补角的度数和为:
.
故答案为170.
【分析】此题考查余角和补角的概念,如果两个角的和等于
平角
,就说这两个角互为补角.如果两个角和为
,则两个角互为余角.根据概念先求出
的余角和补角,再进行相加计算即可.
18.【答案】
149°48′
【解析】【解答】∵
,
∴
,
∵
,
∴
,
∴α的补角为
=
?.
故答案为149°48′.
【分析】首先根据度与分之间的转化关系化简30.2°,然后根据补角的概念计算即可.
三、解答题
19.【答案】
解:设这个角是
,则它的余角为
,补角为
,
由题意得,
,
解得
,
.
答:这个角是
,它的余角是
【解析】【分析】设这个角是
,然后表示出它的余角和补角,再列出方程求解即可.
20.【答案】
解:∵
和
都是直角,
∴
,
∴
,
∴
.
【解析】【分析】先求出∠AOB和∠DOC,再利用∠AOD=∠AOC+∠COD计算即可.
21.【答案】
解:如图,当OC在∠AOB的内部时,∠AOC=∠BOA﹣∠BOC=55°,
当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,
故∠AOC的度数是55°或85°.
【解析】【分析】在同一平面内,若∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB的外部.
22.【答案】
解:如图,
由题意可知,∠ACD=52°,∠BCD=40°,∠CDA=∠CDB=90°,
∴∠CAD=90°﹣∠ACD=90°﹣52°=38°,
∠CBD=90°﹣∠BCD=90°﹣40°=50°,
∴丁岛在甲岛的东偏北38°,
丁岛在乙岛的西偏北50°.
【解析】【分析】本题的关键是求出
,
的值,然后分别以甲、乙为中心,看方向角即可。
一、单选题(共12题
)
1.如图,点
在直线
上,
.若
,则
的大小为(
???)
A.????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
2.如图,将一副三角板按不同位置摆放,其中α和β互为余角的是( )
A.??????B.??????C.??????D.?
3.如图,点
相对于点
的方向是(???
)
A.?南偏东
????????????????????????B.?北偏西
47°????????????????????????C.?西偏北
47°????????????????????????D.?东偏南
47°
4.如图,有
三个地点,且
,从A地测得B地的方位角是北偏东
,那么从C地测B地的方位角是(???
)
A.?南偏东
?????????????????????B.?南偏西
?????????????????????C.?北偏东
?????????????????????D.?北偏西
5.如图,OA⊥OB,若∠1=55°16′,则∠2的度数是(??
)
A.?35°44′????????????????????????????????B.?34°84′????????????????????????????????C.?34°74′????????????????????????????????D.?34°44′
6.下列说法错误的是(??
)
A.?两个互余的角都是锐角
B.?锐角的补角大于这个角本身
C.?互为补角的两个角不可能都是锐角
D.?锐角大于它的余角
7.如图,从8点钟开始,过了20分钟后,分针与时针所夹的度数是(???
)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
8.
的余角是
,那么
的大小是(???
)
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
9.一个角的余角是它的补角的
,这个角是(??
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
10.北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,過极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道
在点O南偏东70°的方向上,则这条跑道所在射线
与正北方向所成角的度数为( )
A.?160°?????????????????????????????????????B.?110°?????????????????????????????????????C.?70°?????????????????????????????????????D.?20°
11.如图,将一副直角三角尺叠放在一起,使直角顶点重合于点O,则下列说法一定成立的是(??
)
A.?
B.?
C.?
与
互补
D.?
与
互余
12.如图所示,点B在点O的北偏东60°,射线
与射线
所成的角是110°,则射线
的方向是(??
)
A.?北偏西30°?????????????????????????B.?北偏西40°?????????????????????????C.?西偏北50°?????????????????????????D.?北偏西50°
二、填空题(共6题
)
13.若两个角的两边两两互相平行,且一个角的
等于另一个角的
,则这两个角的度数分别为________度,________度
14.钟表在7点50分时,时针和分针所成的角是________.
15.
________°.
16.如果一个角的补角是120°,那么这个角的余角的度数是________.
17.已知
,则它的余角与补角的度数和等于________
.
18.若
,则α的补角
________.(用“度、分”表示).
三、综合题(共4题
)
19.已知一个角的余角比这个角的补角的一半还少
,求这个角及它的余角
用方程做
.
20.如图,
和
都是直角,若
,求
的度数.
21.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
22.如图,有甲、乙、丙、丁四个小岛,甲、乙、丙在同一条直线上,而且乙、丙在甲的正东方,丁岛在丙岛的正北方,甲岛在丁岛的南偏西52°方向,乙岛在丁岛的南偏东40°方向.那么,丁岛分别在甲岛和乙岛的什么方向?
答案解析部分
一、单选题
1.【答案】
A
【解析】【解答】解:∵点
在直线
上,
,
∴
,
,
∵
,
∴
,
∴
;
故答案为:A.
【分析】先利用平角求出的度数,再利用直角求出即可。
2.【答案】
B
【解析】【解答】解:A:α=β,不合题意;
B:α+β=90゜,符合题意;
C:α+β=270°,不合题意;
D:α+β=180゜,不合题意;
故答案为:B
【分析】根据互为余角的两个角相加等于90°,进行求解即可。
3.【答案】
B
【解析】【解答】解:如图,由余角的定义,得
,
所以点
在点
的北偏西
47°
.
故答案为:B.
【分析】由余角的定义,求出
,据此判断即可.
4.【答案】
A
【解析】【解答】解:如图,
∵AF//DE
,
∴∠ABE=∠FAB=43°,
∵AB⊥BC
,
∴∠ABC=90°,
∴∠CBD=47°,
∴C地在B地的北偏西47°的方向上.
∴从C地测B地的方位角是南偏东
故答案为:A
.
【分析】根据方向角的概念和平行线的性质求解,即可得出从C地测得B地的方位角。
5.【答案】
D
【解析】【解答】解:∵OA⊥OB,若∠1=55°16′,
∴∠1+∠2=90°,
∴∠2=90°-55°16′=34°44′.
故答案为:D.
【分析】利用垂直的定义可证得∠1+∠2=90°,再代入∠1的度数,可求出∠2的度数.
6.【答案】
D
【解析】【解答】解:A、两角互余,和为90°,两角均为锐角,故A选项不符合题意;
B、两角互补,和为180°,从而锐角的补角必为钝角,故B选项不符合题意;
C、两角互补,和为180°,两锐角的和必小于180°,故C选项不符合题意;
D、两角互余,和为90°,从而锐角不一定大于它的余角,也可以小于或者等于它的余角,故D选项不符合题意.
故答案为:D.
【分析】互为余角的两个角的和等于90°,互为补角的两个角的和等于180°,据此逐一判断即可.
7.【答案】
B
【解析】【解答】解:时针超过20分所走的度数为20×0.5=10°,
分针与8点之间的夹角为4×30=120°,
∴此时时钟面上的时针与分针的夹角是120+10=130°.
故选:B.
【分析】此时时针超过8点,
分针指向4
,
根据每2个数字之间相隔30度和时针1分钟走0.5度可得夹角度数.
8.【答案】
D
【解析】【解答】解:
的余角是
,
,
故答案为:D.
【分析】利用余角的性质求解即可。
9.【答案】
A
【解析】【解答】解:设这个角的度数是x°,则
,
解得:x=30,即这个角的度数是30°,
故答案为:A.
【分析】根据
一个角的余角是它的补角的??
可得
,
再解方程即可。
10.【答案】
B
【解析】【解答】解:∵
在点O南偏东
的方向上,
∴射线
与正北方向所成角的度数为:180°-70°=110°,
故答案为:B.
【分析】根据方向角及邻补角的定义进行解答即可.
11.【答案】
C
【解析】【解答】∵∠AOD=90°-∠DOC,
∠BOC=90°-∠DOC,
∴∠AOD=∠BOC,
∴∠AOB=∠AOD
+∠BOD=∠AOD+90°
∠COD+90°,故A错误;
∠AOB=∠AOD
+∠COD+∠BOC=2∠AOD+∠COD
2∠COD,故B错误;
∠AOB=∠AOC+∠DOB-∠DOC=90°+90°-∠COD=180°-∠COD,
∴∠AOB+∠COD=180°,即∠AOB与∠COD互补,故C正确,D错误;
故答案为:C.
【分析】A、根据同角的余角相等得出∠AOD=∠BOC,从而得出∠AOB=∠AOD+90°,即可判断A错误;
B、利用∠AOB=∠AOD
+∠COD+∠BOC得出∠AOB=2∠AOD+∠COD,即可判断B错误;
CD、利用∠AOB=∠AOC+∠DOB-∠DOC得出∠AOB=180°-∠COD,得出∠AOB与∠COD互补,即可判断C正确,D错误.
12.【答案】
D
【解析】【解答】解:∵射线OC与射线OB所成的角是110°,
∴∠COB=110°,
∵点B在点O的北偏东60°,
∴射线OB与正北方向所成的角是60°
∴射线OC与正北方向所成的角是110°-60°=50°,
∴射线OC的方向是北偏西50°.
故答案为:D.
【分析】根据射线OB和射线OC所成的角是110°,可得∠COB的度数,再根据角的和差关系求解即可得出OC与正北方向所成的角,从而解决问题.
二、填空题
13.【答案】
72;108
【解析】【解答】解:设较小的角的度数为x,则较大的角的度数为x
根据题意可得,x+x=180°
解得,x=72°
∴x=×72°=108°
【分析】根据题意,如果两个角的两边互相平行,则这两个角相等或互补,根据题意列出方程求出答案即可。
14.【答案】
65°
【解析】【解答】解:
7点50分时
时针转动了50×0.5=25°,
则时针和8之间还有30°-25°=5°,
故时针和分针之间夹角为30°×2+5°=65°.
故答案为:65°.
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,找出时针一分钟转0.5°,分针一分钟转6°,所以时针和分针所成的角是30°×2+5°=65°.
15.【答案】
65.7225
【解析】【解答】解:
,
,
故答案为:65.7225.
【分析】利用度分秒之间的关系进行转化即可.
16.【答案】
30°
【解析】【解答】解:∵一个角的补角是120°,
∴这个角为:180°?120°=60°,
∴这个角的余角为:90°?60°=30°.
故答案为:30°.
【分析】和为90°的两个角互为余角,和为180°的两个角互为补角,根据定义即可解答.
17.【答案】
170
【解析】【解答】解:
,
根据互为补角的概念,得
的补角为:
,
根据互为余角的概念,得,
的余角为:
,
余角与补角的度数和为:
.
故答案为170.
【分析】此题考查余角和补角的概念,如果两个角的和等于
平角
,就说这两个角互为补角.如果两个角和为
,则两个角互为余角.根据概念先求出
的余角和补角,再进行相加计算即可.
18.【答案】
149°48′
【解析】【解答】∵
,
∴
,
∵
,
∴
,
∴α的补角为
=
?.
故答案为149°48′.
【分析】首先根据度与分之间的转化关系化简30.2°,然后根据补角的概念计算即可.
三、解答题
19.【答案】
解:设这个角是
,则它的余角为
,补角为
,
由题意得,
,
解得
,
.
答:这个角是
,它的余角是
【解析】【分析】设这个角是
,然后表示出它的余角和补角,再列出方程求解即可.
20.【答案】
解:∵
和
都是直角,
∴
,
∴
,
∴
.
【解析】【分析】先求出∠AOB和∠DOC,再利用∠AOD=∠AOC+∠COD计算即可.
21.【答案】
解:如图,当OC在∠AOB的内部时,∠AOC=∠BOA﹣∠BOC=55°,
当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,
故∠AOC的度数是55°或85°.
【解析】【分析】在同一平面内,若∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB的外部.
22.【答案】
解:如图,
由题意可知,∠ACD=52°,∠BCD=40°,∠CDA=∠CDB=90°,
∴∠CAD=90°﹣∠ACD=90°﹣52°=38°,
∠CBD=90°﹣∠BCD=90°﹣40°=50°,
∴丁岛在甲岛的东偏北38°,
丁岛在乙岛的西偏北50°.
【解析】【分析】本题的关键是求出
,
的值,然后分别以甲、乙为中心,看方向角即可。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
