贵州省贞丰二中2011-2012学年高二下学期4月月考数学(文)试题
文档属性
| 名称 | 贵州省贞丰二中2011-2012学年高二下学期4月月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-16 00:00:00 | ||
图片预览



文档简介
贵州省贞丰二中2011-2012学年高二下学期4月月考文科数学试题
I 卷
一、选择题
1.已知a,b是不共线的向量,=λa+b,=a+μb (λ,μ∈R)那么A,B,C三点共线的充要条件为( )
A.λ+μ=2 B.λ-μ=1 C.λμ=-1 D.λμ=1
【答案】D
2.已知两点 ,O为坐标原点,点C在第二象限,且,则等于( )
A. B. C.-1 D. 1
【答案】A
【解析】作图
[
由已知
3.在△ABC所在平面上有三点P、Q、R,满足++=,++=,++=,则△PQR的面积与△ABC的面积之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
【答案】B
4. 已知平行四边形的三个顶点A.B.C的坐标分别是..,则顶点的坐标为( )
A. B. C. D.
【答案】B
5.已知向量,,若与共线,则等于( )
A.; B. C. D.
【答案】C
6.两列火车从同一站台沿相反方向开去,走了相同的路程,设两列火车的位移向量分别为a和b,则下列说法中错误的是( )
A.a与b为平行向量
B.a与b为模相等的向量
C.a与b为共线向量
D.a与b为相等的向量
【答案】D
7.已知A,B,C是锐角的三个内角,向量,则的夹角是( )
A.锐角 B.钝角 C.直角 D.不确定
【答案】B
8.已知O、A、B是平面上的三个点,直线AB上有一点C,满足2+=0,则=( )
A.2- B.-+2
C. - D.-+
【答案】A
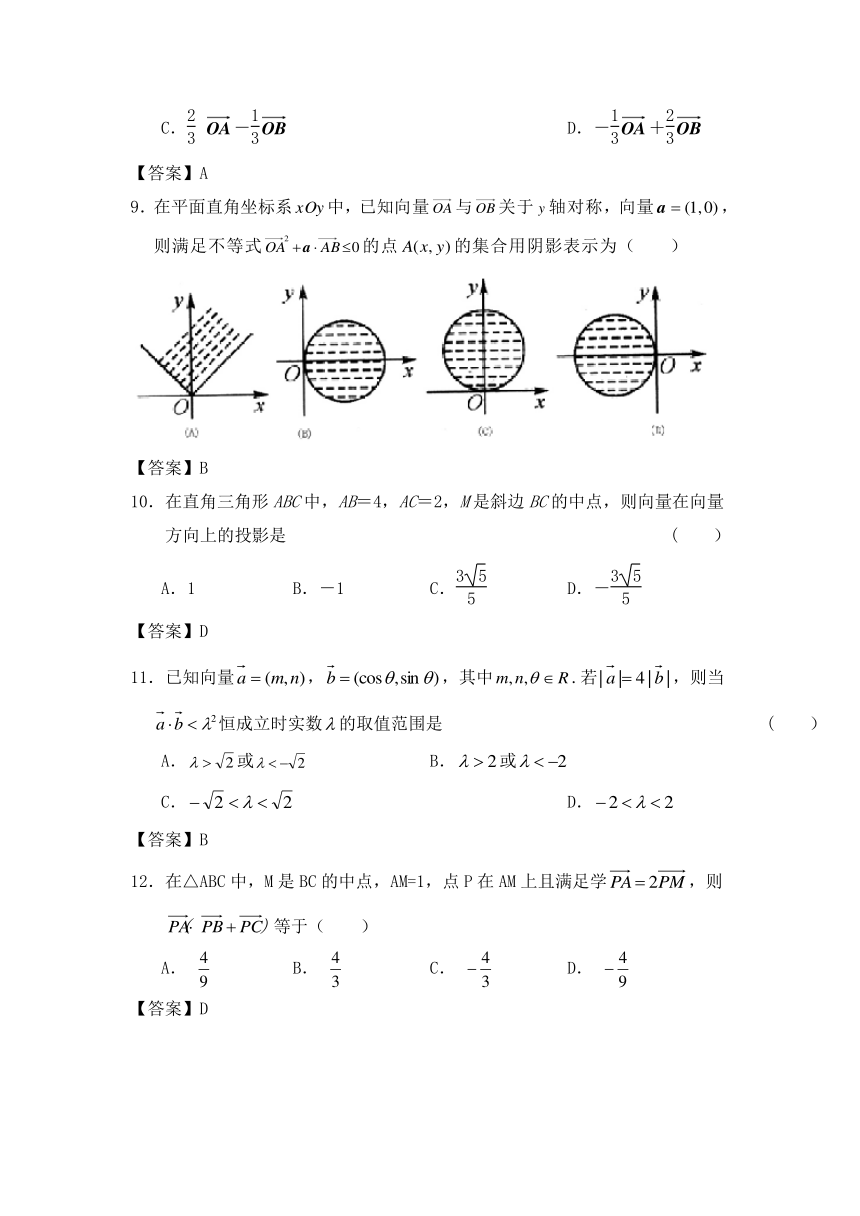
9.在平面直角坐标系中,已知向量与关于轴对称,向量,则满足不等式的点的集合用阴影表示为( )
【答案】B
10.在直角三角形ABC中,AB=4,AC=2,M是斜边BC的中点,则向量在向量方向上的投影是 ( )
A.1 B.-1 C. D.-
【答案】D
11.已知向量,,其中.若,则当恒成立时实数的取值范围是 ( )
A.或 B.或
C. D.
【答案】B
12.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足学,则等于( )
A. B. C. D.
【答案】D
II卷
二、填空题
13.已知向量a=(,1),b=(0,-1),c=(k,).若a-2b与c共线,则k=________.
【答案】1
14.设P是△ABC所在平面内一点,+=2,则点P与边AC的关系是________________________________________________________________________.
【答案】P是AC的中点
15.设,已知两个向量,,则向量长度的最大值是 ;
【答案】
16. 已知平面向量,,与垂直,则=
【答案】
三、解答题
17.如图,在△ABC中,,, ,则 。
【答案】
18.已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61.
(1)求a与b的夹角;
(2)求|a+b|;
(3)若=a,=b,求△ABC的面积.
【答案】(1)由(2a-3b)·(2a+b)=61,
得4|a|2-4a·b-3|b|2=61,
∵|a|=4,|b|=3,
代入上式得a·b=-6,
∴cos θ===-.
又0°≤θ≤180°,∴θ=120°.
(2)|a+b|2=(a+b)2=|a|2+2a·b+|b|2=42+2×(-6)+32=13,
∴|a+b|=.
(3)由(1)知∠BAC=θ=120°,=|a|=4, = |b| =3,
∴=sin∠BAC=×3×4×sin 120°=3.
19.已知向量m=(cos,1),n=(sin,cos2).
(1)若m·n=1,求cos(-x)的值;
(2)记f(x)=m·n,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
【答案】(1)m·n=sincos+cos2
=sin+cos+=sin(+)+.
∵m·n=1,
∴sin(+)=.
∴cos(x+)=1-2sin2(+)=.
∴cos(-x)=-cos(x+)=-.
(2)∵(2a-c)cosB=bcosC,由正弦定理得:
(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0.
∴cosB=,B=.
∴0∴<+<,又∵f(x)=m·n=sin(+)+,
∴f(A)=sin(+)+.
故函数f(A)的取值范围是(1,).
20.已知为坐标原点,向量
,点满足.
(1)记函数,求函数的最小正周期;
(2)若、、三点共线,求的值.
【答案】(1),
,.
,
.
(2)由O,P,C三点共线可得
,得,
,
.
21.已知向量=,,向量=(,-1)
(1)若,求的值;
(2)若恒成立,求实数的取值范围。
【答案】 (1)∵,∴,得,又,所以;
(2)∵=,
所以,
又 ∈[0,],∴,∴,
∴的最大值为16,∴的最大值为4,又恒成立,所以。
22.已知锐角△ABC三个内角为A,B,C,向量p=(cosA+sinA,2-2sinA),向量q=(cosA-sinA,1+sinA),且p⊥q.
(1)求角A;
(2)设AC=,sin2A+sin2B=sin2C,求△ABC的面积.
【答案】(1)∵p⊥q,
∴(cosA+sinA)(cosA-sinA)+(2-2sinA)(1+sinA)=0,
∴sin2A=.而A为锐角,所以sinA= A=.
(2)由正弦定理得a2+b2=c2,
∴△ABC是直角三角形,且∠C=.
∴BC=AC×tan=×=3.
∴S△ABC=AC·BC=××3=.
I 卷
一、选择题
1.已知a,b是不共线的向量,=λa+b,=a+μb (λ,μ∈R)那么A,B,C三点共线的充要条件为( )
A.λ+μ=2 B.λ-μ=1 C.λμ=-1 D.λμ=1
【答案】D
2.已知两点 ,O为坐标原点,点C在第二象限,且,则等于( )
A. B. C.-1 D. 1
【答案】A
【解析】作图
[
由已知
3.在△ABC所在平面上有三点P、Q、R,满足++=,++=,++=,则△PQR的面积与△ABC的面积之比为( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
【答案】B
4. 已知平行四边形的三个顶点A.B.C的坐标分别是..,则顶点的坐标为( )
A. B. C. D.
【答案】B
5.已知向量,,若与共线,则等于( )
A.; B. C. D.
【答案】C
6.两列火车从同一站台沿相反方向开去,走了相同的路程,设两列火车的位移向量分别为a和b,则下列说法中错误的是( )
A.a与b为平行向量
B.a与b为模相等的向量
C.a与b为共线向量
D.a与b为相等的向量
【答案】D
7.已知A,B,C是锐角的三个内角,向量,则的夹角是( )
A.锐角 B.钝角 C.直角 D.不确定
【答案】B
8.已知O、A、B是平面上的三个点,直线AB上有一点C,满足2+=0,则=( )
A.2- B.-+2
C. - D.-+
【答案】A
9.在平面直角坐标系中,已知向量与关于轴对称,向量,则满足不等式的点的集合用阴影表示为( )
【答案】B
10.在直角三角形ABC中,AB=4,AC=2,M是斜边BC的中点,则向量在向量方向上的投影是 ( )
A.1 B.-1 C. D.-
【答案】D
11.已知向量,,其中.若,则当恒成立时实数的取值范围是 ( )
A.或 B.或
C. D.
【答案】B
12.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足学,则等于( )
A. B. C. D.
【答案】D
II卷
二、填空题
13.已知向量a=(,1),b=(0,-1),c=(k,).若a-2b与c共线,则k=________.
【答案】1
14.设P是△ABC所在平面内一点,+=2,则点P与边AC的关系是________________________________________________________________________.
【答案】P是AC的中点
15.设,已知两个向量,,则向量长度的最大值是 ;
【答案】
16. 已知平面向量,,与垂直,则=
【答案】
三、解答题
17.如图,在△ABC中,,, ,则 。
【答案】
18.已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61.
(1)求a与b的夹角;
(2)求|a+b|;
(3)若=a,=b,求△ABC的面积.
【答案】(1)由(2a-3b)·(2a+b)=61,
得4|a|2-4a·b-3|b|2=61,
∵|a|=4,|b|=3,
代入上式得a·b=-6,
∴cos θ===-.
又0°≤θ≤180°,∴θ=120°.
(2)|a+b|2=(a+b)2=|a|2+2a·b+|b|2=42+2×(-6)+32=13,
∴|a+b|=.
(3)由(1)知∠BAC=θ=120°,=|a|=4, = |b| =3,
∴=sin∠BAC=×3×4×sin 120°=3.
19.已知向量m=(cos,1),n=(sin,cos2).
(1)若m·n=1,求cos(-x)的值;
(2)记f(x)=m·n,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
【答案】(1)m·n=sincos+cos2
=sin+cos+=sin(+)+.
∵m·n=1,
∴sin(+)=.
∴cos(x+)=1-2sin2(+)=.
∴cos(-x)=-cos(x+)=-.
(2)∵(2a-c)cosB=bcosC,由正弦定理得:
(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0.
∴cosB=,B=.
∴0
∴f(A)=sin(+)+.
故函数f(A)的取值范围是(1,).
20.已知为坐标原点,向量
,点满足.
(1)记函数,求函数的最小正周期;
(2)若、、三点共线,求的值.
【答案】(1),
,.
,
.
(2)由O,P,C三点共线可得
,得,
,
.
21.已知向量=,,向量=(,-1)
(1)若,求的值;
(2)若恒成立,求实数的取值范围。
【答案】 (1)∵,∴,得,又,所以;
(2)∵=,
所以,
又 ∈[0,],∴,∴,
∴的最大值为16,∴的最大值为4,又恒成立,所以。
22.已知锐角△ABC三个内角为A,B,C,向量p=(cosA+sinA,2-2sinA),向量q=(cosA-sinA,1+sinA),且p⊥q.
(1)求角A;
(2)设AC=,sin2A+sin2B=sin2C,求△ABC的面积.
【答案】(1)∵p⊥q,
∴(cosA+sinA)(cosA-sinA)+(2-2sinA)(1+sinA)=0,
∴sin2A=.而A为锐角,所以sinA= A=.
(2)由正弦定理得a2+b2=c2,
∴△ABC是直角三角形,且∠C=.
∴BC=AC×tan=×=3.
∴S△ABC=AC·BC=××3=.
同课章节目录
