1.2.2矩形的性质与判定2 课件(共33张PPT)
文档属性
| 名称 | 1.2.2矩形的性质与判定2 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览




文档简介
(共33张PPT)
1.2.2矩形的性质与判定2
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.会证明矩形的判定定理.
2.能运用矩形的判定定理进行简单的计算与证明.
3.能运用矩形的性质定理与判定定理进行比较简单的综合推理与证明.
学习目标
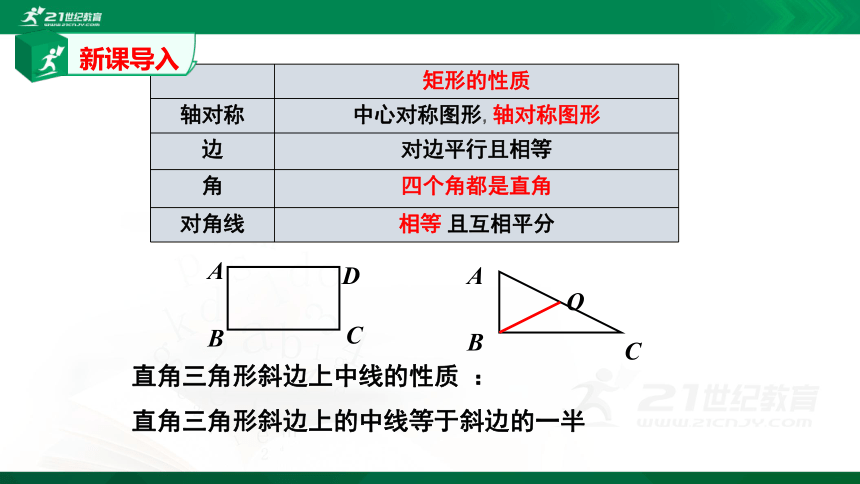
矩形的性质
轴对称
中心对称图形,轴对称图形
边
对边平行且相等
角
四个角都是直角
对角线
相等
且互相平分
直角三角形斜边上中线的性质
:
直角三角形斜边上的中线等于斜边的一半
A
D
C
B
A
B
C
O
新课导入
思考
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
新课导入
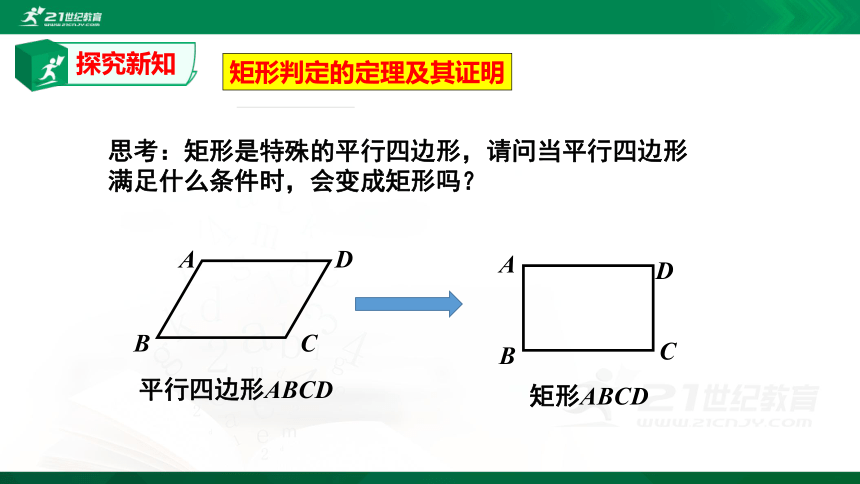
矩形判定的定理及其证明
思考:矩形是特殊的平行四边形,请问当平行四边形满足什么条件时,会变成矩形吗?
A
B
C
D
平行四边形ABCD
A
D
C
B
矩形ABCD
探究新知
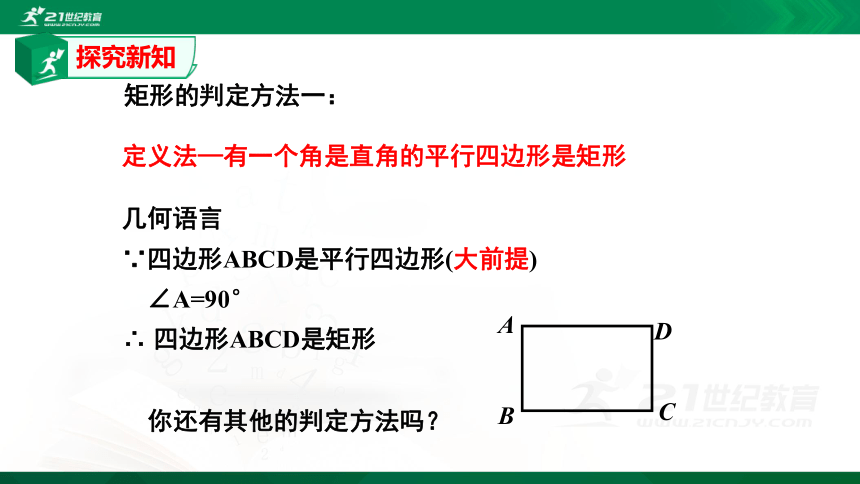
定义法—有一个角是直角的平行四边形是矩形
几何语言
∵四边形ABCD是平行四边形(大前提)
∠A=90°
∴
四边形ABCD是矩形
矩形的判定方法一:
A
D
C
B
你还有其他的判定方法吗?
探究新知
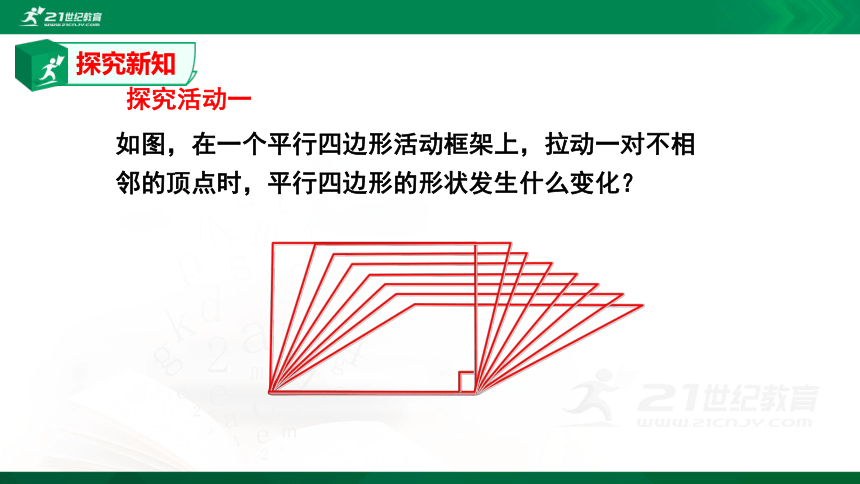
如图,在一个平行四边形活动框架上,拉动一对不相邻的顶点时,平行四边形的形状发生什么变化?
探究活动一
探究新知
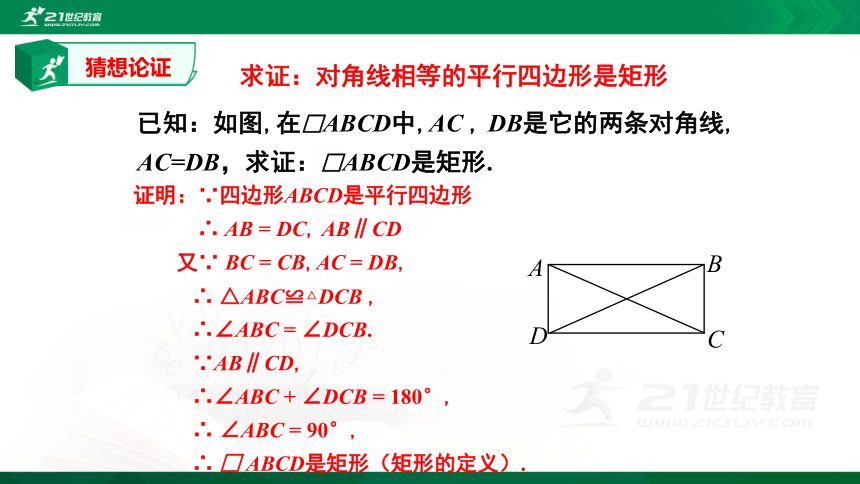
猜想:对角线相等的平行四边形是矩形
问题:这个运动过程中,两条对角线的长度会发生变化吗?当两条对角线相等时,平行四边形有什么特征?
探究新知
已知:如图,在□ABCD中,AC
,
DB是它的两条对角线,
AC=DB,求证:□ABCD是矩形.
A
B
C
D
证明:∵四边形ABCD是平行四边形
∴
AB
=
DC,
AB∥CD
又∵
BC
=
CB,AC
=
DB,
∴
△ABC≌△DCB
,
∴∠ABC
=
∠DCB.
∵AB∥CD,
∴∠ABC
+
∠DCB
=
180°,
∴
∠ABC
=
90°,
∴
□
ABCD是矩形(矩形的定义).
求证:对角线相等的平行四边形是矩形
猜想论证
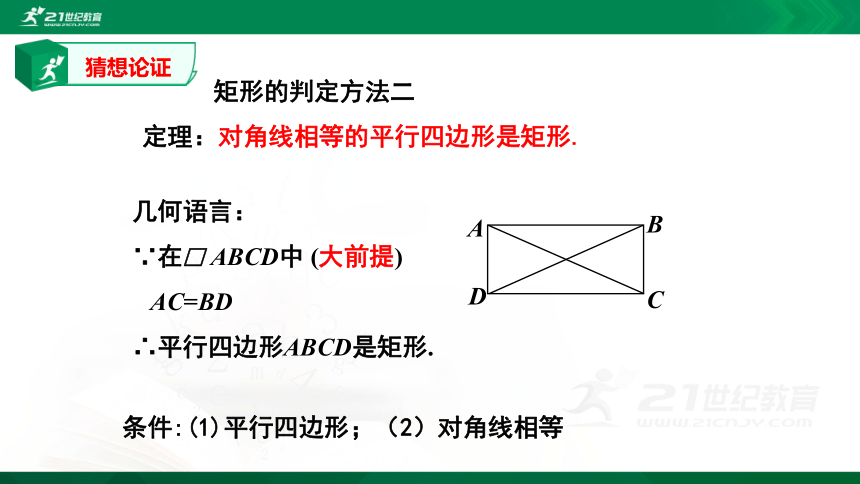
定理:对角线相等的平行四边形是矩形.
几何语言:
∵在□
ABCD中
(大前提)
AC=BD
∴平行四边形ABCD是矩形.
A
B
C
D
矩形的判定方法二
条件:(1)平行四边形;(2)对角线相等
猜想论证
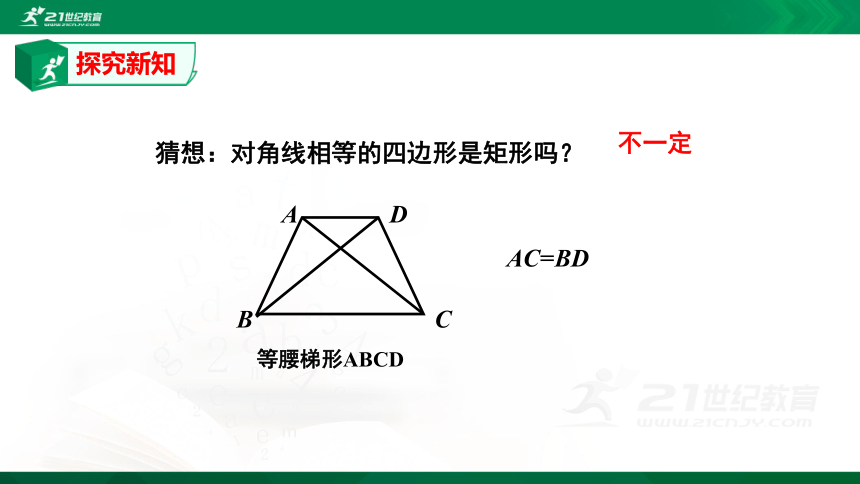
不一定
猜想:对角线相等的四边形是矩形吗?
A
B
C
D
AC=BD
等腰梯形ABCD
探究新知
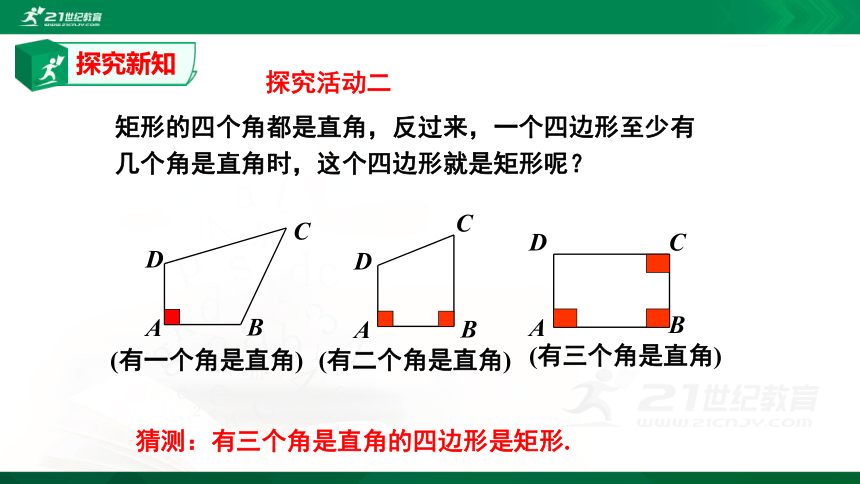
矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
探究活动二
探究新知
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形
∵
∠A=90°
∴四边形ABCD是矩形(矩形的定义).
A
B
C
D
求证:有三个角是直角的四边形是矩形.
猜想论证
定理:有三个角是直角的四边形是矩形.
几何语言:
∵在四边形ABCD中
∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
矩形的判定方法三
A
B
C
D
猜想论证
归纳总结
矩形的判定方法
几何语言
定义法
有一个角是直角的平行四边形是矩形
∵□ABCD,
∠A=90°,
∴
四边形ABCD是矩形
定理
对角线相等的平行四边形是矩形
∵□ABCD,
AC=BD,
∴
四边形ABCD是矩形
定理
有三个角是直角的四边形是矩形
∵四边形ABCD中,
∠A=∠B=∠C=90°
∴四边形ABCD是矩形.
A
B
C
D
A
B
C
D
定理的应用
例1:如图,在□ABCD中,对角线AC与BD相交于点O
,
△ABO是等边三角形,
AB=4,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴OA=
OC,OB
=
OD.
又∵△ABO是等边三角形,
∴OA=
OB=AB=
4,∠BAC=60°.
∴AC=
BD=
2OA
=
2×4
=
8.
A
B
C
D
O
探究新知
∴□ABCD是矩形
(对角线相等的平行四边形是矩形).
∴∠ABC=90°(矩形的四个角都是直角)
.
在Rt△ABC中,由勾股定理,得
AB2
+
BC2
=AC2
,
∴BC=
.
∴S□ABCD=AB·BC=4×
=
A
B
C
D
O
探究新知
例2:如图,在△ABC中,
AB=AC,D为BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD
,
EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
证明:(1)∵△ABC是等腰三角形,
∴∠B=∠ACB.
又∵四边形ABDE是平行四边形,
∴∠B=∠EDC,AB=DE,
∴∠ACB=∠EDC,
∴△ADC≌△ECD.
A
D
C
E
B
例题讲解
(2)∵AB=AC,BD=CD,
∴AD⊥BC,∴∠ADC=90°.
∵四边形ABDE是平行四边形,
∴AE平行且等于BD,即AE平行且等于DC,
∴四边形ADCE是平行四边形.
而∠ADC=90°,
∴四边形ADCE是矩形.
A
D
C
E
B
例题讲解
例3
如图,在
ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC=
AC,
OB=OD=
BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
例题讲解
例4
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分),
∵
AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
例题讲解
例5
如图,
□?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形
EFGH为矩形.
证明:在□?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴
∠BAE+
∠ABF=
∠DAB+
∠ABC=90°.
例题讲解
例6
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=
∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=
∠CAM,
∴∠DAE=∠DAC+∠CAE
=
(∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
例题讲解
1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC
C.AB=BC
D.AC=BD
D
2.若矩形两邻边的长度之比为2︰3,面积为54cm2,
则其周长为(
).
A.15cm
B.30cm
C.45cm
D.90cm
B
课堂练习
3.下列命题是真命题的是(
)
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形
D.对角线互相垂直的四边形是矩形
C
5.若矩形两对角线相交所成的角等于120°,较长边为6cm,则该矩形的对角线长为
cm。
4.四边形ABCD中,∠A=∠B
=∠C=∠D,
则四边形ABCD是
;
矩形
6.已知:如图,
ABCD中,∠DAC
=∠ADB,
求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴OA=
AC,OD=
BD,
∵∠DAC=∠ADB,
∴OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
7.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
求证:四边形ABCD是矩形.
证明:∵AB∥CD,∠BAD=90°,
∴∠ADC=90°.
又∵△ABC中,AB=5,BC=12,AC=13,
满足132=52+122,即
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
A
B
C
D
8.如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.
D
A
B
C
E
O
解:四边形CEDO是矩形.
理由如下:已知四边形ABCD是菱形.
∴AC⊥BD.
∴∠BOC=90°.
∵DE∥AC,CE∥BD,
∴四边形CEDO是平行四边形.
∴四边形CEDO是矩形(矩形的定义).
9.如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,使ON=OB,再延长OC至M,使CM=AN.求证:四边形NDMB为矩形.
证明:∵四边形ABCD为平行四边形,
∴AO=OC,OD=OB.
∵AN=CM,ON=OB,
∴ON=OM=OD=OB,
∴四边形NDMB为平行四边形,MN=BD,
∴平行四边形NDMB为矩形.
1.判定一个四边形是矩形的方法与思路是:
2.用定义判定一个四边形是矩形必须满足两个条件:
(1)有一个角是直角;(2)是平行四边形.
3.用对角线判定一个四边形是矩形,也必须满足
两个条件:
(1)对角线相等;
(2)是平行四边形.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.2.2矩形的性质与判定2
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.会证明矩形的判定定理.
2.能运用矩形的判定定理进行简单的计算与证明.
3.能运用矩形的性质定理与判定定理进行比较简单的综合推理与证明.
学习目标
矩形的性质
轴对称
中心对称图形,轴对称图形
边
对边平行且相等
角
四个角都是直角
对角线
相等
且互相平分
直角三角形斜边上中线的性质
:
直角三角形斜边上的中线等于斜边的一半
A
D
C
B
A
B
C
O
新课导入
思考
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
新课导入
矩形判定的定理及其证明
思考:矩形是特殊的平行四边形,请问当平行四边形满足什么条件时,会变成矩形吗?
A
B
C
D
平行四边形ABCD
A
D
C
B
矩形ABCD
探究新知
定义法—有一个角是直角的平行四边形是矩形
几何语言
∵四边形ABCD是平行四边形(大前提)
∠A=90°
∴
四边形ABCD是矩形
矩形的判定方法一:
A
D
C
B
你还有其他的判定方法吗?
探究新知
如图,在一个平行四边形活动框架上,拉动一对不相邻的顶点时,平行四边形的形状发生什么变化?
探究活动一
探究新知
猜想:对角线相等的平行四边形是矩形
问题:这个运动过程中,两条对角线的长度会发生变化吗?当两条对角线相等时,平行四边形有什么特征?
探究新知
已知:如图,在□ABCD中,AC
,
DB是它的两条对角线,
AC=DB,求证:□ABCD是矩形.
A
B
C
D
证明:∵四边形ABCD是平行四边形
∴
AB
=
DC,
AB∥CD
又∵
BC
=
CB,AC
=
DB,
∴
△ABC≌△DCB
,
∴∠ABC
=
∠DCB.
∵AB∥CD,
∴∠ABC
+
∠DCB
=
180°,
∴
∠ABC
=
90°,
∴
□
ABCD是矩形(矩形的定义).
求证:对角线相等的平行四边形是矩形
猜想论证
定理:对角线相等的平行四边形是矩形.
几何语言:
∵在□
ABCD中
(大前提)
AC=BD
∴平行四边形ABCD是矩形.
A
B
C
D
矩形的判定方法二
条件:(1)平行四边形;(2)对角线相等
猜想论证
不一定
猜想:对角线相等的四边形是矩形吗?
A
B
C
D
AC=BD
等腰梯形ABCD
探究新知
矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形呢?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
探究活动二
探究新知
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形
∵
∠A=90°
∴四边形ABCD是矩形(矩形的定义).
A
B
C
D
求证:有三个角是直角的四边形是矩形.
猜想论证
定理:有三个角是直角的四边形是矩形.
几何语言:
∵在四边形ABCD中
∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
矩形的判定方法三
A
B
C
D
猜想论证
归纳总结
矩形的判定方法
几何语言
定义法
有一个角是直角的平行四边形是矩形
∵□ABCD,
∠A=90°,
∴
四边形ABCD是矩形
定理
对角线相等的平行四边形是矩形
∵□ABCD,
AC=BD,
∴
四边形ABCD是矩形
定理
有三个角是直角的四边形是矩形
∵四边形ABCD中,
∠A=∠B=∠C=90°
∴四边形ABCD是矩形.
A
B
C
D
A
B
C
D
定理的应用
例1:如图,在□ABCD中,对角线AC与BD相交于点O
,
△ABO是等边三角形,
AB=4,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴OA=
OC,OB
=
OD.
又∵△ABO是等边三角形,
∴OA=
OB=AB=
4,∠BAC=60°.
∴AC=
BD=
2OA
=
2×4
=
8.
A
B
C
D
O
探究新知
∴□ABCD是矩形
(对角线相等的平行四边形是矩形).
∴∠ABC=90°(矩形的四个角都是直角)
.
在Rt△ABC中,由勾股定理,得
AB2
+
BC2
=AC2
,
∴BC=
.
∴S□ABCD=AB·BC=4×
=
A
B
C
D
O
探究新知
例2:如图,在△ABC中,
AB=AC,D为BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD
,
EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
证明:(1)∵△ABC是等腰三角形,
∴∠B=∠ACB.
又∵四边形ABDE是平行四边形,
∴∠B=∠EDC,AB=DE,
∴∠ACB=∠EDC,
∴△ADC≌△ECD.
A
D
C
E
B
例题讲解
(2)∵AB=AC,BD=CD,
∴AD⊥BC,∴∠ADC=90°.
∵四边形ABDE是平行四边形,
∴AE平行且等于BD,即AE平行且等于DC,
∴四边形ADCE是平行四边形.
而∠ADC=90°,
∴四边形ADCE是矩形.
A
D
C
E
B
例题讲解
例3
如图,在
ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC=
AC,
OB=OD=
BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
例题讲解
例4
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分),
∵
AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
例题讲解
例5
如图,
□?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形
EFGH为矩形.
证明:在□?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴
∠BAE+
∠ABF=
∠DAB+
∠ABC=90°.
例题讲解
例6
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=
∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=
∠CAM,
∴∠DAE=∠DAC+∠CAE
=
(∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
例题讲解
1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC
C.AB=BC
D.AC=BD
D
2.若矩形两邻边的长度之比为2︰3,面积为54cm2,
则其周长为(
).
A.15cm
B.30cm
C.45cm
D.90cm
B
课堂练习
3.下列命题是真命题的是(
)
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形
D.对角线互相垂直的四边形是矩形
C
5.若矩形两对角线相交所成的角等于120°,较长边为6cm,则该矩形的对角线长为
cm。
4.四边形ABCD中,∠A=∠B
=∠C=∠D,
则四边形ABCD是
;
矩形
6.已知:如图,
ABCD中,∠DAC
=∠ADB,
求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴OA=
AC,OD=
BD,
∵∠DAC=∠ADB,
∴OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
7.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
求证:四边形ABCD是矩形.
证明:∵AB∥CD,∠BAD=90°,
∴∠ADC=90°.
又∵△ABC中,AB=5,BC=12,AC=13,
满足132=52+122,即
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
A
B
C
D
8.如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形CEDO是矩形吗?说出你的理由.
D
A
B
C
E
O
解:四边形CEDO是矩形.
理由如下:已知四边形ABCD是菱形.
∴AC⊥BD.
∴∠BOC=90°.
∵DE∥AC,CE∥BD,
∴四边形CEDO是平行四边形.
∴四边形CEDO是矩形(矩形的定义).
9.如图,平行四边形ABCD中,对角线AC、BD相交于点O,延长OA到N,使ON=OB,再延长OC至M,使CM=AN.求证:四边形NDMB为矩形.
证明:∵四边形ABCD为平行四边形,
∴AO=OC,OD=OB.
∵AN=CM,ON=OB,
∴ON=OM=OD=OB,
∴四边形NDMB为平行四边形,MN=BD,
∴平行四边形NDMB为矩形.
1.判定一个四边形是矩形的方法与思路是:
2.用定义判定一个四边形是矩形必须满足两个条件:
(1)有一个角是直角;(2)是平行四边形.
3.用对角线判定一个四边形是矩形,也必须满足
两个条件:
(1)对角线相等;
(2)是平行四边形.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
