1.3.1正方形的性质与判定1 课件(共35张PPT)
文档属性
| 名称 | 1.3.1正方形的性质与判定1 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 09:50:46 | ||
图片预览





文档简介
(共35张PPT)
1.3.1正方形的性质与判定1
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系.
2.掌握正方形的性质,能正确运用正方形的性质解题.
学习目标
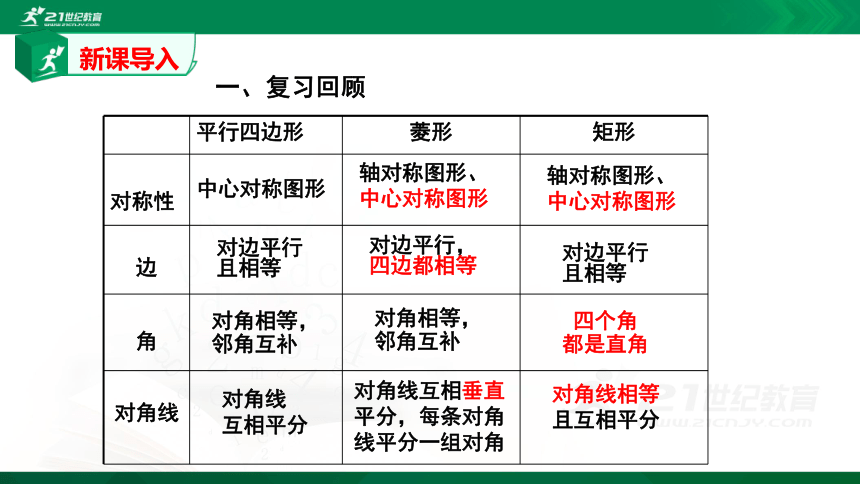
平行四边形
菱形
矩形
对称性
边
角
对角线
一、复习回顾
中心对称图形
轴对称图形、中心对称图形
轴对称图形、中心对称图形
对边平行
且相等
对边平行
且相等
对边平行,
四边都相等
对角相等,
邻角互补
对角相等,
邻角互补
四个角
都是直角
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
新课导入
二、图片欣赏
新课导入
思考;在我们的生活中除了矩形、菱形外,还有什么特殊的平行四边形呢?
菱形
矩形
正方形
新课导入
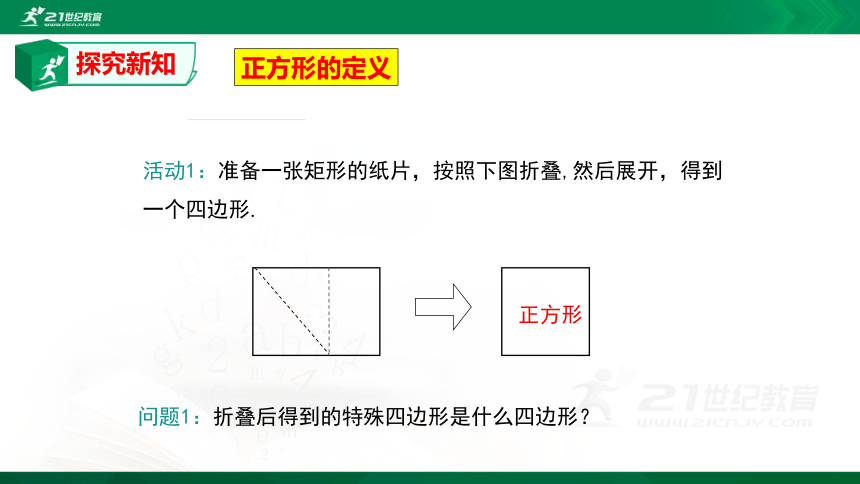
正方形的定义
活动1:准备一张矩形的纸片,按照下图折叠,然后展开,得到一个四边形.
问题1:折叠后得到的特殊四边形是什么四边形?
正方形
探究新知
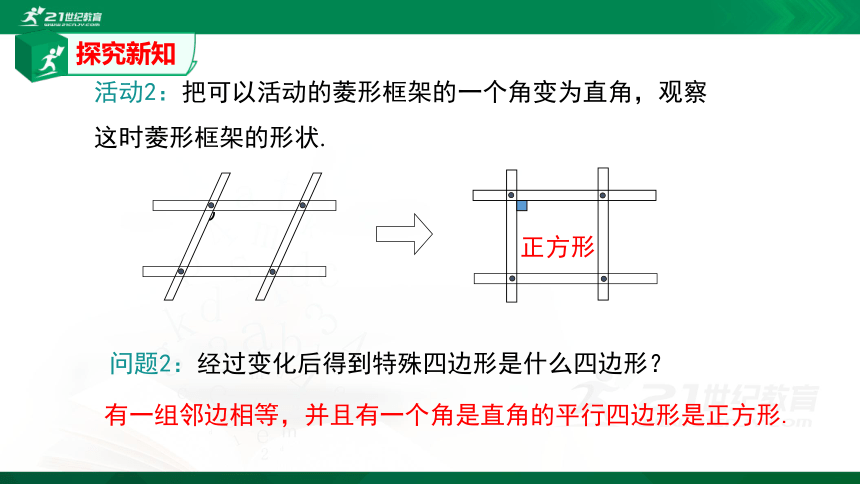
活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.
问题2:经过变化后得到特殊四边形是什么四边形?
有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
正方形
探究新知
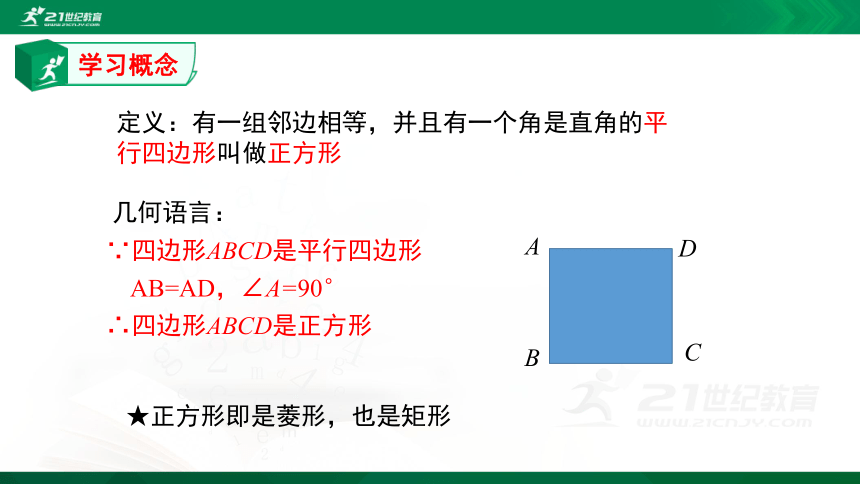
定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
几何语言:
∵四边形ABCD是平行四边形
AB=AD,∠A=90°
∴四边形ABCD是正方形
学习概念
★正方形即是菱形,也是矩形
A
D
C
B
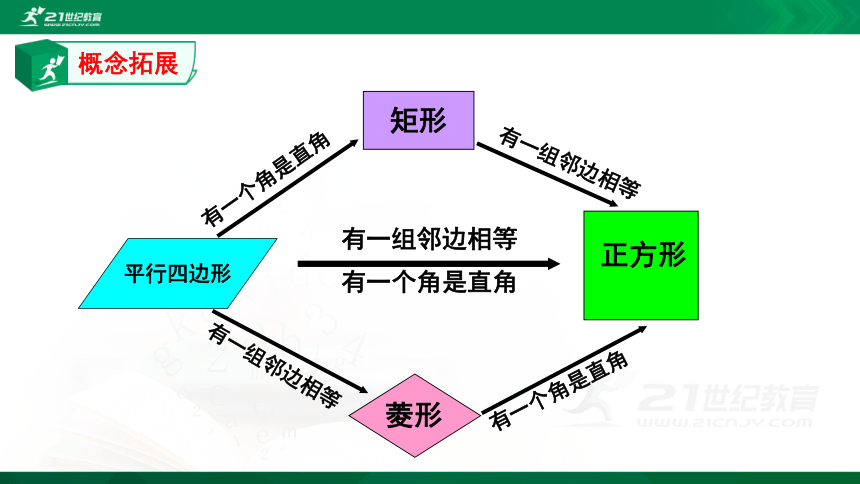
概念拓展
平行四边形
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
有一个角是直角
有一组邻边相等
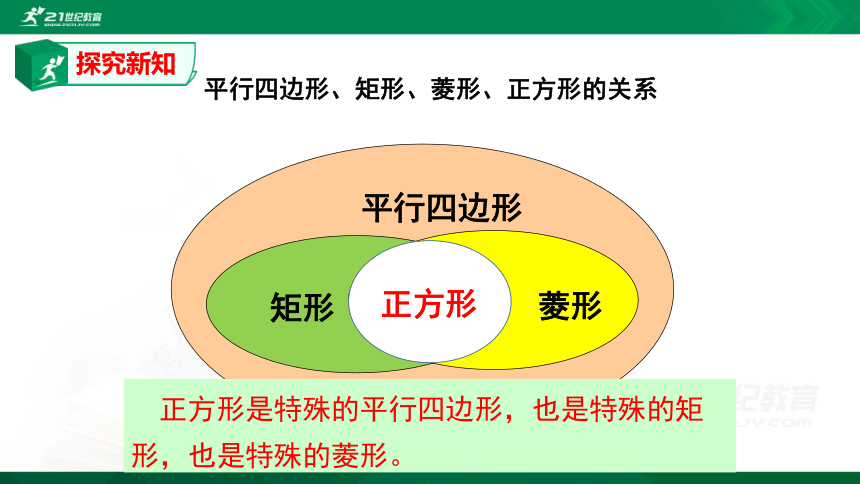
平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
探究新知
正方形的性质探究和证明
猜想:正方形是特殊的矩形,也是特殊的菱形。
?
正方形的性质=
菱形性质
矩形性质
探究新知
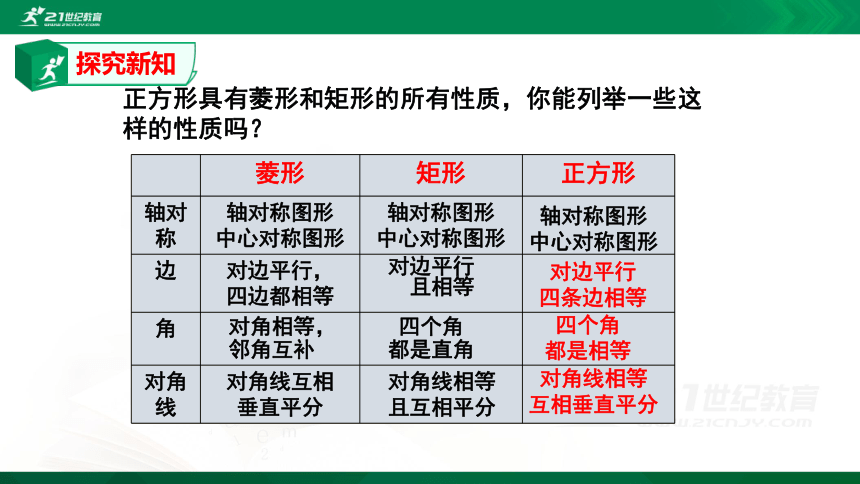
正方形具有菱形和矩形的所有性质,你能列举一些这样的性质吗?
菱形
矩形
正方形
轴对称
轴对称图形
中心对称图形
轴对称图形
中心对称图形
边
对边平行,
四边都相等
对边平行
且相等
角
对角相等,
邻角互补
四个角
都是直角
对角线
对角线互相
垂直平分
对角线相等
且互相平分
轴对称图形
中心对称图形
对边平行
四条边相等
四个角
都是相等
对角线相等
互相垂直平分
探究新知
(1)正方形的四个角都是直角,四条边相等.
(2)正方形的对角线相等且互相垂直平分.
正方形有4条对称轴.
探究新知
已知:如图,四边形ABCD是平行四边形,
∠A=90°,
AB=AD
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是平行四边形.
∠A=90°,
AB=AD.
∴四边形ABCD是矩形
四边形ABCD是菱形
∴∠A=∠B
=∠C
=∠D
=
90°,
AB=
BC=CD=AD.
求证:正方形的四个角都是直角,四条边相等.
探究新知
已知:如图,四边形ABCD是平行四边形,∠A=90°,
AB=AD
,对角线AC、BD相交于点O.
求证:AO=CO=BO=DO,AC⊥BD.
A
B
C
D
O
求证:正方形的对角线相等且互相垂直平分.
证明:∵四边形ABCD是平行四边形.
∠A=90°,
AB=AD.
∴四边形ABCD是矩形,
四边形ABCD是菱形
∴
AO=CO=BO=DO,
AC⊥BD.
探究新知
正方形的性质
定理:
正方形的四个角都是直角,四条边相等.
定理:
正方形的对角线相等且互相垂直平分
A
B
C
D
A
B
C
D
O
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
AB=BC=CD=AD
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD
OA=OB=OC=OD
探究新知
对边平行且相等
每条对角线平分一组对角
对角线相等
对角线互相垂直
对角线互相平分
四个角都是直角
对角相等
四条边都相等
性质
正方形
菱形
矩形
平行四边形
图形
拓展延伸
对比归纳
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
探究新知
正方形性质定理的应用
例1:如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.
BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形.
∴BC=DC,∠BCE
=90°
.
(正方形的四条边都相等,四个角都是直角)
∴∠DCF=180°-∠BCE=180°-90°=90°.
A
B
D
C
F
E
探究新知
A
B
D
F
E
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
(2)延长BE交DE于点M,
∵△BCE≌△DCF
,
∴∠CBE
=∠CDF.
∵∠DCF
=90°
,
∴∠CDF
+∠F
=90°.∴∠CBE+∠F=90°
,
∴∠BMF=90°.
∴BE⊥DF.
C
M
探究新知
如图,正方形ABCD中,AF=BE,
AF与BE相交于点O,
(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数;
变式练习一
D
A
C
B
F
E
证明:(1)∵四边形ABCD是正方形.
∴AD=AB,∠DAB=∠ABC
=90°
.
又∵
AF=BE
∴
△DAF≌△ABE(SAS).
探究新知
如图,正方形ABCD中,AF=BE,
AF与BE相交于点O,
(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数;
变式练习一
证明:(2)∵
△DAF≌△ABE
∴
∠ADF=∠BAE
∵
∠DAB
=90°
.
∴
∠ADF+
AFD=
90°
∴
∠BAE
+
AFD=
90°
∴DF
⊥AE
∴
∠AOE=
90°
D
A
C
B
F
E
O
探究新知
如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
变式练习二
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°.
而F是CB的延长线上的点,
∴∠ABF=90°.
在△ADE和△ABF中,
AB=AD,∠ABF=∠ADE,BF=DE,
∴△ADE≌△ABF(SAS).
探究新知
如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(2)若BC=8,DE=6,求△AEF的面积.
变式练习二
(2)解:∵BC=8,∴AD=8.
在Rt△ADE中,∴AE
=
=10.
∵
△ADE≌△ABF
∴AE=AF,
∠FAB=
∠EAD,
∠EAF=
∠FAB
+
∠BAE
=
∠EAD
+∠BAE
=90°.
∴S△AEF的面积=1/2AE2=1/2×100=50.
探究新知
例2:如图,已知四边形ABCD是正方形,对角线AC与BD相交于点O
,
MN∥AB
,且分别于OA
,
OB相交于点M
,
N.
求证:(1)BM
=
CN;(2)BM⊥CN.
A
B
C
D
O
M
N
证明:(1)∵MN∥AB.
∴∠1
=∠2
=∠3
=∠4
=
45°.
∴OM
=
ON.
∵OA=
OB,
∴OA-
OM
=
OB
-
ON,AM=BN.
又∵∠2=∠NBC,AB=BC.
∴△ABM
≌△BCN(SAS)
∴BM=CN.
1
2
3
4
例题讲解
A
B
C
D
O
M
N
(2)延长CN交线段MB于点Q.
∵△ABM≌△BCN.
∴∠6=∠8.
∵∠OCB
=∠ABO
=45°.
∴∠5=∠7.
又∵∠ONC=∠QNB.
∴180°-∠5
-∠ONC
=
180°-∠7
-∠QNB,
∠CON
=∠NQB
=
90°.
∴BM⊥CN.
Q
5
7
6
8
例题讲解
2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
课堂练习
3.在正方形ABC中,∠ADB=
,∠DAC=
,
∠BOC=
.
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是
.
A
D
B
C
O
A
D
B
C
O
E
45°
90°
22.5°
第3题
第4题
45°
5.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为1和2,则正方形的边长是_____.
6.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1,以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,则EE′的长等于_______.
2
7.如图,已知正方形ABCD
,以AB为边向正方形外作等边△ABE,连结DE
、
CE
,求∠DEC的度数.
D
A
E
B
C
解:∵△ABE是等边三角形.
∴AB
=AE=BE,
∠ABE=∠BEA=∠EAB
=60°.
又∵四边形ABCD是正方形.
∴AD=BC=AE=BE,
∠DAB=∠ABC=90°.
∴∠DAE=∠CBE=150°.
∴∠AED=∠EDA=∠CEB=∠BCE=15°.
∴∠DEC=∠AEB-∠AED-∠CEB=30°.
8.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD=
,
面积为AD2=8.
9.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=(
-1)cm,
∴BE=(
-1)cm.
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.3.1正方形的性质与判定1
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系.
2.掌握正方形的性质,能正确运用正方形的性质解题.
学习目标
平行四边形
菱形
矩形
对称性
边
角
对角线
一、复习回顾
中心对称图形
轴对称图形、中心对称图形
轴对称图形、中心对称图形
对边平行
且相等
对边平行
且相等
对边平行,
四边都相等
对角相等,
邻角互补
对角相等,
邻角互补
四个角
都是直角
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
新课导入
二、图片欣赏
新课导入
思考;在我们的生活中除了矩形、菱形外,还有什么特殊的平行四边形呢?
菱形
矩形
正方形
新课导入
正方形的定义
活动1:准备一张矩形的纸片,按照下图折叠,然后展开,得到一个四边形.
问题1:折叠后得到的特殊四边形是什么四边形?
正方形
探究新知
活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.
问题2:经过变化后得到特殊四边形是什么四边形?
有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
正方形
探究新知
定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
几何语言:
∵四边形ABCD是平行四边形
AB=AD,∠A=90°
∴四边形ABCD是正方形
学习概念
★正方形即是菱形,也是矩形
A
D
C
B
概念拓展
平行四边形
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
有一个角是直角
有一组邻边相等
平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
探究新知
正方形的性质探究和证明
猜想:正方形是特殊的矩形,也是特殊的菱形。
?
正方形的性质=
菱形性质
矩形性质
探究新知
正方形具有菱形和矩形的所有性质,你能列举一些这样的性质吗?
菱形
矩形
正方形
轴对称
轴对称图形
中心对称图形
轴对称图形
中心对称图形
边
对边平行,
四边都相等
对边平行
且相等
角
对角相等,
邻角互补
四个角
都是直角
对角线
对角线互相
垂直平分
对角线相等
且互相平分
轴对称图形
中心对称图形
对边平行
四条边相等
四个角
都是相等
对角线相等
互相垂直平分
探究新知
(1)正方形的四个角都是直角,四条边相等.
(2)正方形的对角线相等且互相垂直平分.
正方形有4条对称轴.
探究新知
已知:如图,四边形ABCD是平行四边形,
∠A=90°,
AB=AD
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是平行四边形.
∠A=90°,
AB=AD.
∴四边形ABCD是矩形
四边形ABCD是菱形
∴∠A=∠B
=∠C
=∠D
=
90°,
AB=
BC=CD=AD.
求证:正方形的四个角都是直角,四条边相等.
探究新知
已知:如图,四边形ABCD是平行四边形,∠A=90°,
AB=AD
,对角线AC、BD相交于点O.
求证:AO=CO=BO=DO,AC⊥BD.
A
B
C
D
O
求证:正方形的对角线相等且互相垂直平分.
证明:∵四边形ABCD是平行四边形.
∠A=90°,
AB=AD.
∴四边形ABCD是矩形,
四边形ABCD是菱形
∴
AO=CO=BO=DO,
AC⊥BD.
探究新知
正方形的性质
定理:
正方形的四个角都是直角,四条边相等.
定理:
正方形的对角线相等且互相垂直平分
A
B
C
D
A
B
C
D
O
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
AB=BC=CD=AD
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD
OA=OB=OC=OD
探究新知
对边平行且相等
每条对角线平分一组对角
对角线相等
对角线互相垂直
对角线互相平分
四个角都是直角
对角相等
四条边都相等
性质
正方形
菱形
矩形
平行四边形
图形
拓展延伸
对比归纳
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
探究新知
正方形性质定理的应用
例1:如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.
BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形.
∴BC=DC,∠BCE
=90°
.
(正方形的四条边都相等,四个角都是直角)
∴∠DCF=180°-∠BCE=180°-90°=90°.
A
B
D
C
F
E
探究新知
A
B
D
F
E
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
(2)延长BE交DE于点M,
∵△BCE≌△DCF
,
∴∠CBE
=∠CDF.
∵∠DCF
=90°
,
∴∠CDF
+∠F
=90°.∴∠CBE+∠F=90°
,
∴∠BMF=90°.
∴BE⊥DF.
C
M
探究新知
如图,正方形ABCD中,AF=BE,
AF与BE相交于点O,
(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数;
变式练习一
D
A
C
B
F
E
证明:(1)∵四边形ABCD是正方形.
∴AD=AB,∠DAB=∠ABC
=90°
.
又∵
AF=BE
∴
△DAF≌△ABE(SAS).
探究新知
如图,正方形ABCD中,AF=BE,
AF与BE相交于点O,
(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数;
变式练习一
证明:(2)∵
△DAF≌△ABE
∴
∠ADF=∠BAE
∵
∠DAB
=90°
.
∴
∠ADF+
AFD=
90°
∴
∠BAE
+
AFD=
90°
∴DF
⊥AE
∴
∠AOE=
90°
D
A
C
B
F
E
O
探究新知
如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
变式练习二
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°.
而F是CB的延长线上的点,
∴∠ABF=90°.
在△ADE和△ABF中,
AB=AD,∠ABF=∠ADE,BF=DE,
∴△ADE≌△ABF(SAS).
探究新知
如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(2)若BC=8,DE=6,求△AEF的面积.
变式练习二
(2)解:∵BC=8,∴AD=8.
在Rt△ADE中,∴AE
=
=10.
∵
△ADE≌△ABF
∴AE=AF,
∠FAB=
∠EAD,
∠EAF=
∠FAB
+
∠BAE
=
∠EAD
+∠BAE
=90°.
∴S△AEF的面积=1/2AE2=1/2×100=50.
探究新知
例2:如图,已知四边形ABCD是正方形,对角线AC与BD相交于点O
,
MN∥AB
,且分别于OA
,
OB相交于点M
,
N.
求证:(1)BM
=
CN;(2)BM⊥CN.
A
B
C
D
O
M
N
证明:(1)∵MN∥AB.
∴∠1
=∠2
=∠3
=∠4
=
45°.
∴OM
=
ON.
∵OA=
OB,
∴OA-
OM
=
OB
-
ON,AM=BN.
又∵∠2=∠NBC,AB=BC.
∴△ABM
≌△BCN(SAS)
∴BM=CN.
1
2
3
4
例题讲解
A
B
C
D
O
M
N
(2)延长CN交线段MB于点Q.
∵△ABM≌△BCN.
∴∠6=∠8.
∵∠OCB
=∠ABO
=45°.
∴∠5=∠7.
又∵∠ONC=∠QNB.
∴180°-∠5
-∠ONC
=
180°-∠7
-∠QNB,
∠CON
=∠NQB
=
90°.
∴BM⊥CN.
Q
5
7
6
8
例题讲解
2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
课堂练习
3.在正方形ABC中,∠ADB=
,∠DAC=
,
∠BOC=
.
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是
.
A
D
B
C
O
A
D
B
C
O
E
45°
90°
22.5°
第3题
第4题
45°
5.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为1和2,则正方形的边长是_____.
6.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1,以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,则EE′的长等于_______.
2
7.如图,已知正方形ABCD
,以AB为边向正方形外作等边△ABE,连结DE
、
CE
,求∠DEC的度数.
D
A
E
B
C
解:∵△ABE是等边三角形.
∴AB
=AE=BE,
∠ABE=∠BEA=∠EAB
=60°.
又∵四边形ABCD是正方形.
∴AD=BC=AE=BE,
∠DAB=∠ABC=90°.
∴∠DAE=∠CBE=150°.
∴∠AED=∠EDA=∠CEB=∠BCE=15°.
∴∠DEC=∠AEB-∠AED-∠CEB=30°.
8.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD=
,
面积为AD2=8.
9.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=(
-1)cm,
∴BE=(
-1)cm.
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
