1.3.2正方形的性质与判定2 课件(共30张PPT)
文档属性
| 名称 | 1.3.2正方形的性质与判定2 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览




文档简介
(共30张PPT)
1.3.2正方形的性质与判定2
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.掌握正方形的判定方法.
2.会运用正方形的判定条件进行有关的论证和计算
学习目标
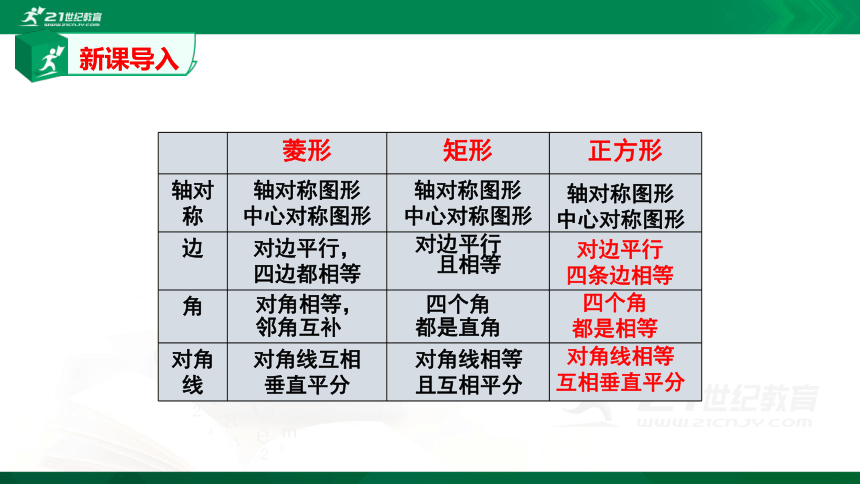
菱形
矩形
正方形
轴对称
轴对称图形
中心对称图形
轴对称图形
中心对称图形
边
对边平行,
四边都相等
对边平行
且相等
角
对角相等,
邻角互补
四个角
都是直角
对角线
对角线互相
垂直平分
对角线相等
且互相平分
轴对称图形
中心对称图形
对边平行
四条边相等
四个角
都是相等
对角线相等
互相垂直平分
新课导入
矩形、菱形的判定方法
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
三个判定定理
定义
对角线相等
定义
对角线垂直
新课导入
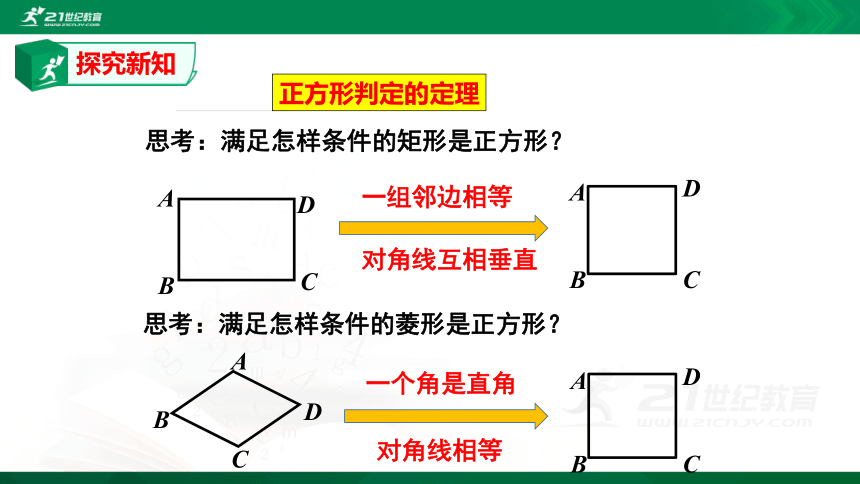
正方形判定的定理
思考:满足怎样条件的矩形是正方形?
一组邻边相等
对角线互相垂直
思考:满足怎样条件的菱形是正方形?
一个角是直角
对角线相等
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
探究新知
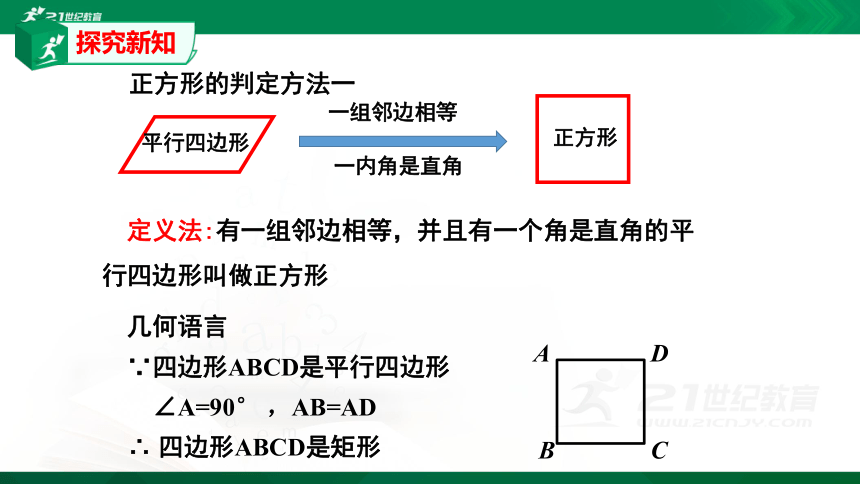
定义法:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
几何语言
∵四边形ABCD是平行四边形
∠A=90°
,AB=AD
∴
四边形ABCD是矩形
正方形的判定方法一
A
B
C
D
平行四边形
正方形
一组邻边相等
一内角是直角
探究新知
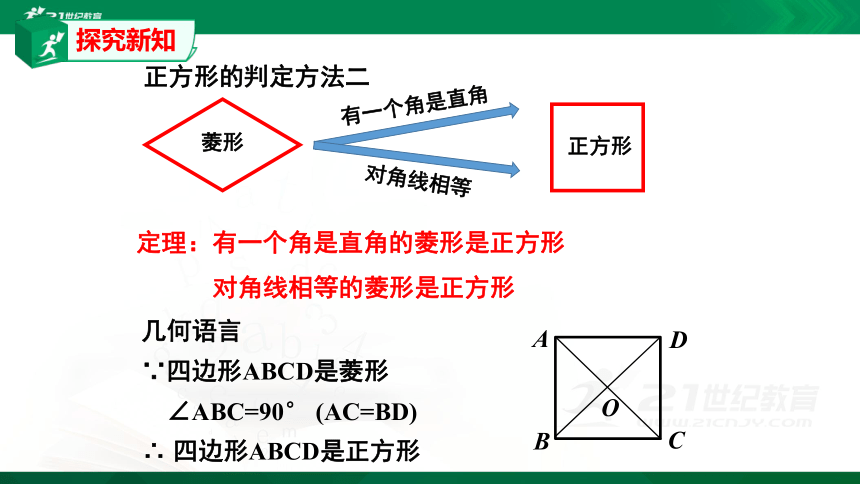
定理:有一个角是直角的菱形是正方形
对角线相等的菱形是正方形
几何语言
∵四边形ABCD是菱形
∠ABC=90°
(AC=BD)
∴
四边形ABCD是正方形
正方形的判定方法二
正方形
有一个角是直角
对角线相等
菱形
A
B
C
D
O
探究新知
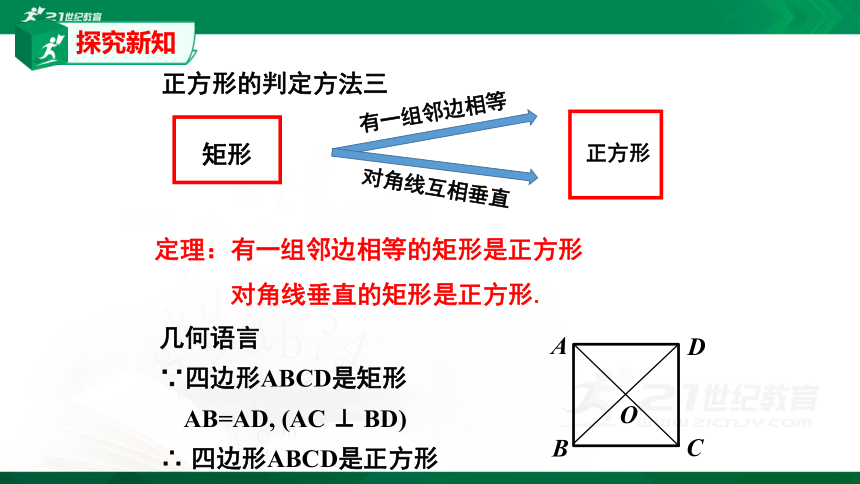
定理:有一组邻边相等的矩形是正方形
对角线垂直的矩形是正方形.
几何语言
∵四边形ABCD是矩形
AB=AD,
(AC
⊥
BD)
∴
四边形ABCD是正方形
正方形的判定方法三
正方形
有一组邻边相等
对角线互相垂直
A
B
C
D
O
矩形
探究新知
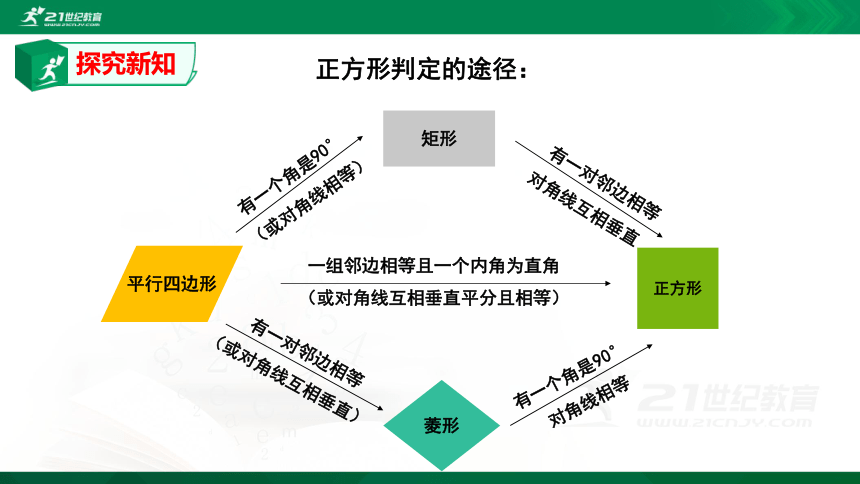
有一个角是90°
(或对角线相等)
有一对邻边相等
(或对角线互相垂直)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)
有一个角是90°
对角线相等
有一对邻边相等
对角线互相垂直
正方形判定的途径:
探究新知
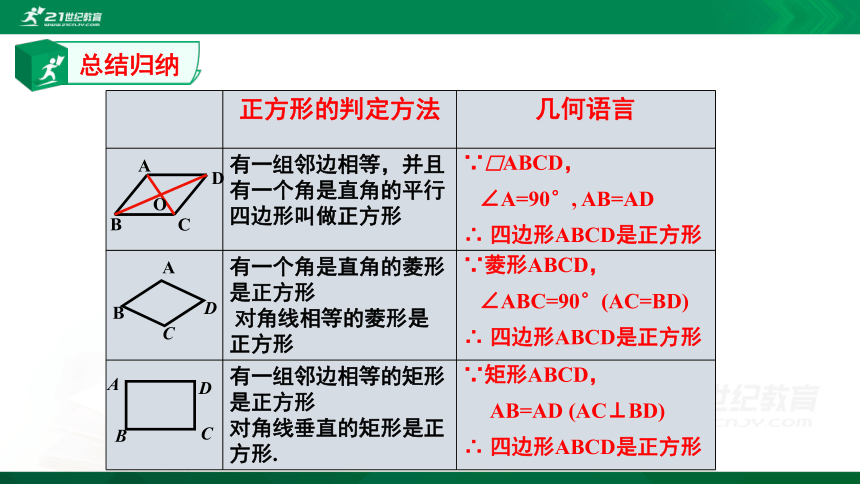
总结归纳
正方形的判定方法
几何语言
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
∵□ABCD,
∠A=90°,
AB=AD
∴
四边形ABCD是正方形
有一个角是直角的菱形是正方形
对角线相等的菱形是正方形
∵菱形ABCD,
∠ABC=90°(AC=BD)
∴
四边形ABCD是正方形
有一组邻边相等的矩形是正方形
对角线垂直的矩形是正方形.
∵矩形ABCD,
AB=AD
(AC⊥BD)
∴
四边形ABCD是正方形
A
B
C
D
A
D
C
B
A
B
C
D
O
正方形判定定理的应用
例1:如图,在矩形ABCD中,
BE平分∠ABC
,
CE平分∠DCB
,
BF∥CE
,
CF∥BE.
求证:四边形BECF是正方形.
F
A
B
E
C
D
解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形;
45°
45°
探究新知
F
A
B
E
C
D
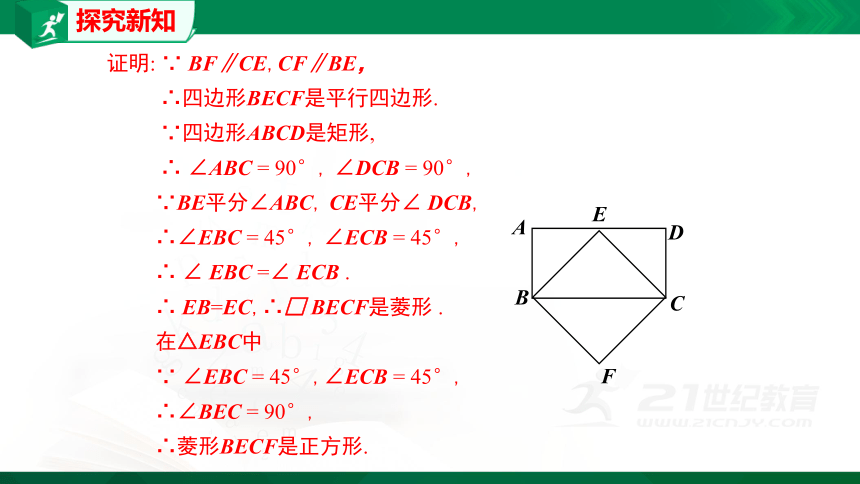
证明:
∵
BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴
∠ABC
=
90°,
∠DCB
=
90°,
∵BE平分∠ABC,
CE平分∠
DCB,
∴∠EBC
=
45°,
∠ECB
=
45°,
∴
∠
EBC
=∠
ECB
.
∴
EB=EC,∴□
BECF是菱形
.
在△EBC中
∵
∠EBC
=
45°,∠ECB
=
45°,
∴∠BEC
=
90°,
∴菱形BECF是正方形.
探究新知
例2:已知:如图所示,在Rt△ABC中,
∠C=90°
,
∠BAC
,
∠ABC的平分线于点D
,
DE⊥BC于点E
,
DF⊥AC于点F.
求证:四边形CEDF是正方形.
证明:
如图所示,过点D作DG⊥AB于点G.
∵DF⊥AC
,
DE⊥BC
,
∴∠DFC=∠DEC=90°.
又∠C=90°,
∴四边形CEDF是矩形
(有三个角是直角的四边形是矩形).
∴AD平分∠BAC
,
DF⊥AC
,
DG⊥AB.
∴DF=DG.
同理可得
DE=DG
,
∴DE=DF.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
C
E
B
A
F
D
G
探究新知
例3:如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO
=45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO
≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
B
O
E
H
G
F
探究新知
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO
,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
探究新知
中点四边形
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
A
B
C
D
矩
形
正方形
任意四边形
E
F
G
H
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
平行四边形
菱
形
正方形
探究新知
议一议:
以四边形各边中点为顶点的新四边形的形状主要与原四边形的什么有关?请你说说你发现在结论。
新四边形的形状只与原四边形的两对角线大小、位置关系有关。
对角线相等
对角线互相垂直
矩
形
菱
形
对角线相等且垂直
正方形
特殊四边形的中点四边形:
◆平行四边形的中点四边形是平行四边形
◆矩形的中点四边形是菱形
◆菱形的中点四边形是矩形
◆正方形的中点四边形是正方形
◆等腰梯形的中点四边形是菱形
◆直角梯形的中点四边形是平行四边形
◆梯形的中点四边形是平行四边形
归纳小结
总结归纳
常见中点四边形比较
1.下列命题正确的是(
)
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
2.四个内角都相等的四边形一定是(
)
A.正方形
B.菱形
C.矩形
D.平行四边形
D
C
课堂练习
3.满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形.(
)
(2)对角线互相垂直的矩形.(
)
(3)对角线相等的菱形.(
)
(4)对角线互相垂直平分且相等的四边形.(
)
是
是
是
是
4.
如图,已知四边形ABCD是平行四边形,下列结论不正确的是(
)
A.
当AB=BC时,它是菱形
B.
当∠ABC=90°时,它是矩形
C.
当AC⊥BD时,它是菱形
D.
当AC=BD时,它是正方形
D
5.如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是(
)
AB∥DC
B.
AC=BD
C.
AC⊥BD
D.
AB=DC
C
6.
如图,正方形ABCD的对角线AC,BD相交于点O,OA=3,则此正方形的面积为(
)
A.
3
B.
12
C.
18
D.
36
C
7.如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
求证:四边形ABCD是正方形.
证明:由题意,得∠BAE=∠EAG,
∠DAF=∠FAG,
∴∠BAD=2∠EAF=90°.
∴四边形ABCD是矩形.
∵AB=AG,AD=AG,
∴AB=AD.
∴四边形ABCD是正方形.
8.如图,在四边形ABCD中,
AB=BC
,对角线BD平分∠
ABC
,
P是BD上一点,过点P作PM
⊥
AD
,
PN
⊥
CD
,垂足分别为M、N.
(1)
求证:∠ADB=∠CDB;
(2)
若∠ADC=90°,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(AAS).
∴∠ADB=∠CDB.
1
2
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是矩形(有一组邻边相等的矩形是正方形).
1
.定义法:
2.矩形法:
正方形判定方法
一邻边相等
一个直角
+
+
平行四边形
=
正方形
3.菱形法:
一邻边相等
+
矩形
=
正方形
一个直角
+
菱形
=
正方形
对角线互相垂直
+
矩形
=
正方形
对角线相等
+
菱形
=
正方形
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.3.2正方形的性质与判定2
第一章
特殊平行四边形
2021-2022学年九年级数学上册同步(北师版)
1.掌握正方形的判定方法.
2.会运用正方形的判定条件进行有关的论证和计算
学习目标
菱形
矩形
正方形
轴对称
轴对称图形
中心对称图形
轴对称图形
中心对称图形
边
对边平行,
四边都相等
对边平行
且相等
角
对角相等,
邻角互补
四个角
都是直角
对角线
对角线互相
垂直平分
对角线相等
且互相平分
轴对称图形
中心对称图形
对边平行
四条边相等
四个角
都是相等
对角线相等
互相垂直平分
新课导入
矩形、菱形的判定方法
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
三个判定定理
定义
对角线相等
定义
对角线垂直
新课导入
正方形判定的定理
思考:满足怎样条件的矩形是正方形?
一组邻边相等
对角线互相垂直
思考:满足怎样条件的菱形是正方形?
一个角是直角
对角线相等
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
探究新知
定义法:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
几何语言
∵四边形ABCD是平行四边形
∠A=90°
,AB=AD
∴
四边形ABCD是矩形
正方形的判定方法一
A
B
C
D
平行四边形
正方形
一组邻边相等
一内角是直角
探究新知
定理:有一个角是直角的菱形是正方形
对角线相等的菱形是正方形
几何语言
∵四边形ABCD是菱形
∠ABC=90°
(AC=BD)
∴
四边形ABCD是正方形
正方形的判定方法二
正方形
有一个角是直角
对角线相等
菱形
A
B
C
D
O
探究新知
定理:有一组邻边相等的矩形是正方形
对角线垂直的矩形是正方形.
几何语言
∵四边形ABCD是矩形
AB=AD,
(AC
⊥
BD)
∴
四边形ABCD是正方形
正方形的判定方法三
正方形
有一组邻边相等
对角线互相垂直
A
B
C
D
O
矩形
探究新知
有一个角是90°
(或对角线相等)
有一对邻边相等
(或对角线互相垂直)
平行四边形
矩形
菱形
正方形
一组邻边相等且一个内角为直角
(或对角线互相垂直平分且相等)
有一个角是90°
对角线相等
有一对邻边相等
对角线互相垂直
正方形判定的途径:
探究新知
总结归纳
正方形的判定方法
几何语言
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
∵□ABCD,
∠A=90°,
AB=AD
∴
四边形ABCD是正方形
有一个角是直角的菱形是正方形
对角线相等的菱形是正方形
∵菱形ABCD,
∠ABC=90°(AC=BD)
∴
四边形ABCD是正方形
有一组邻边相等的矩形是正方形
对角线垂直的矩形是正方形.
∵矩形ABCD,
AB=AD
(AC⊥BD)
∴
四边形ABCD是正方形
A
B
C
D
A
D
C
B
A
B
C
D
O
正方形判定定理的应用
例1:如图,在矩形ABCD中,
BE平分∠ABC
,
CE平分∠DCB
,
BF∥CE
,
CF∥BE.
求证:四边形BECF是正方形.
F
A
B
E
C
D
解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形;
45°
45°
探究新知
F
A
B
E
C
D
证明:
∵
BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴
∠ABC
=
90°,
∠DCB
=
90°,
∵BE平分∠ABC,
CE平分∠
DCB,
∴∠EBC
=
45°,
∠ECB
=
45°,
∴
∠
EBC
=∠
ECB
.
∴
EB=EC,∴□
BECF是菱形
.
在△EBC中
∵
∠EBC
=
45°,∠ECB
=
45°,
∴∠BEC
=
90°,
∴菱形BECF是正方形.
探究新知
例2:已知:如图所示,在Rt△ABC中,
∠C=90°
,
∠BAC
,
∠ABC的平分线于点D
,
DE⊥BC于点E
,
DF⊥AC于点F.
求证:四边形CEDF是正方形.
证明:
如图所示,过点D作DG⊥AB于点G.
∵DF⊥AC
,
DE⊥BC
,
∴∠DFC=∠DEC=90°.
又∠C=90°,
∴四边形CEDF是矩形
(有三个角是直角的四边形是矩形).
∴AD平分∠BAC
,
DF⊥AC
,
DG⊥AB.
∴DF=DG.
同理可得
DE=DG
,
∴DE=DF.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
C
E
B
A
F
D
G
探究新知
例3:如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO
=45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO
≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
B
O
E
H
G
F
探究新知
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO
,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
探究新知
中点四边形
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
A
B
C
D
矩
形
正方形
任意四边形
E
F
G
H
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
平行四边形
菱
形
正方形
探究新知
议一议:
以四边形各边中点为顶点的新四边形的形状主要与原四边形的什么有关?请你说说你发现在结论。
新四边形的形状只与原四边形的两对角线大小、位置关系有关。
对角线相等
对角线互相垂直
矩
形
菱
形
对角线相等且垂直
正方形
特殊四边形的中点四边形:
◆平行四边形的中点四边形是平行四边形
◆矩形的中点四边形是菱形
◆菱形的中点四边形是矩形
◆正方形的中点四边形是正方形
◆等腰梯形的中点四边形是菱形
◆直角梯形的中点四边形是平行四边形
◆梯形的中点四边形是平行四边形
归纳小结
总结归纳
常见中点四边形比较
1.下列命题正确的是(
)
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
2.四个内角都相等的四边形一定是(
)
A.正方形
B.菱形
C.矩形
D.平行四边形
D
C
课堂练习
3.满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形.(
)
(2)对角线互相垂直的矩形.(
)
(3)对角线相等的菱形.(
)
(4)对角线互相垂直平分且相等的四边形.(
)
是
是
是
是
4.
如图,已知四边形ABCD是平行四边形,下列结论不正确的是(
)
A.
当AB=BC时,它是菱形
B.
当∠ABC=90°时,它是矩形
C.
当AC⊥BD时,它是菱形
D.
当AC=BD时,它是正方形
D
5.如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是(
)
AB∥DC
B.
AC=BD
C.
AC⊥BD
D.
AB=DC
C
6.
如图,正方形ABCD的对角线AC,BD相交于点O,OA=3,则此正方形的面积为(
)
A.
3
B.
12
C.
18
D.
36
C
7.如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
求证:四边形ABCD是正方形.
证明:由题意,得∠BAE=∠EAG,
∠DAF=∠FAG,
∴∠BAD=2∠EAF=90°.
∴四边形ABCD是矩形.
∵AB=AG,AD=AG,
∴AB=AD.
∴四边形ABCD是正方形.
8.如图,在四边形ABCD中,
AB=BC
,对角线BD平分∠
ABC
,
P是BD上一点,过点P作PM
⊥
AD
,
PN
⊥
CD
,垂足分别为M、N.
(1)
求证:∠ADB=∠CDB;
(2)
若∠ADC=90°,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明:(1)∵AB
=
BC,BD平分∠ABC.
∴∠1=∠2.
∴△ABD≌△CBD
(AAS).
∴∠ADB=∠CDB.
1
2
C
A
B
D
P
M
N
(2)∵∠ADC=90°;
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是矩形(有一组邻边相等的矩形是正方形).
1
.定义法:
2.矩形法:
正方形判定方法
一邻边相等
一个直角
+
+
平行四边形
=
正方形
3.菱形法:
一邻边相等
+
矩形
=
正方形
一个直角
+
菱形
=
正方形
对角线互相垂直
+
矩形
=
正方形
对角线相等
+
菱形
=
正方形
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
