2021-2022学年高一上学期数学北师大版(2019)必修第一册高一期中复习课件:充要条件求参题型大全(共40张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版(2019)必修第一册高一期中复习课件:充要条件求参题型大全(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览










文档简介
(共40张PPT)
充要条件求参题型大全
课件制作
胡琪
1.2常用逻辑用语复习
北师大(2019)必修1
看看这一节我们要学什么
1.根据不等式之间的充分必要关系求参.
2.根据方程之间的充分必要关系求参.
环节一
小推大
有一个圆A,在其内又含有一个圆B.请回答:
1.“点在A内”是“点在B内”的什么条件?
由已知B?A,所以点在B内,能推出点在A内,故“点在A内”是“点在B内”的必要条件.
2.“点在B内”是“点在A内”的什么条件?
因为点在B内?点一定在A内,所以“点在B内”是“点在A内”的充分条件.
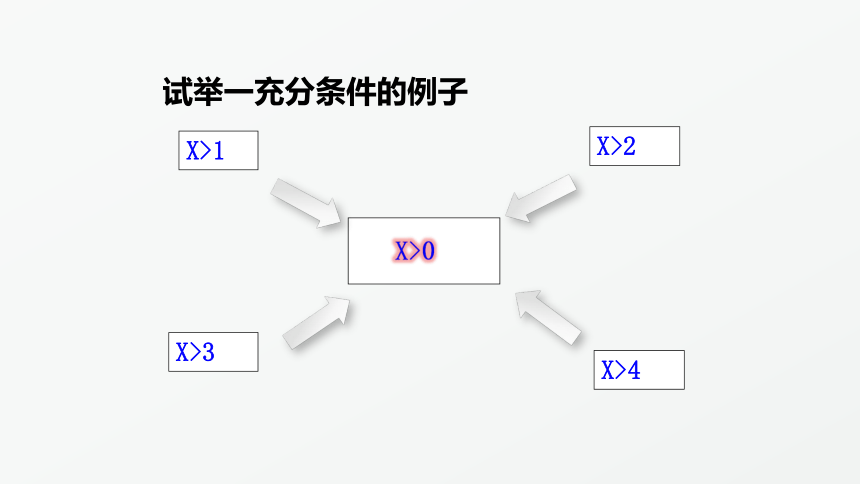
X>0
X>1
X>2
X>3
X>4
试举一充分条件的例子
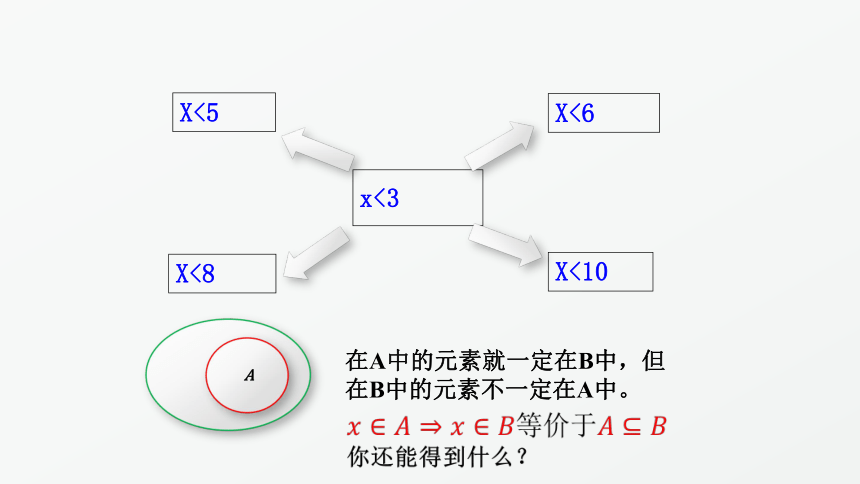
x<3
X<5
X<8
X<10
X<6
B
A
在A中的元素就一定在B中,但在B中的元素不一定在A中。
?
小推大原理
如果一个命题的条件和结论可以用集合表示且这两个集合有大小关系,那么,代表小集合的一方一定能推出代表大集合的一方,而大的不能推出小的,结合充分必要的定义,就可以方便地判断条件的类型。这种方法叫【集合法】
环节二
不等式类型
1.已知p:2x+m>0,q:x-4>0,若p是q的充分条件,则实数m的取值范围是?
A.
角度一
一次不等式
[解析] p:x>-,q:x>4,若p是q的充要条件,∴-≥4,∴m≤-8.
2.已知,,若是的必要不充分条件,则实数a的取值范围是
A.
B.
C.
角度一
一次不等式
因为或,或,且是的必要不充分条件,所以或?{或}
2.已知,,若是的必要不充分条件,则实数a的取值范围是
A.
B.
C.
角度一
一次不等式
所以或解得.
故实数a的取值范围是.
3.已知集合P={x|a-4“x∈P”是“x∈Q”的必要条件,求实数a的取值范围.
角度一
一次不等式
解:因为“x∈P”是x∈Q的必要条件,所以Q?P.
所以{x|1解得-1≤a≤5,即实数a的取值范围是[-1,5].
4.已知集合A=,B={x|x≥m+1或x≤m-1},命题
p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数
m的取值范围.
A.
B.
C.
角度一
一次不等式
解:因为命题p是命题q的充分条件,所以A?B.所以m+1≤,或m-1≥2,解得m≤-,或m≥3.故实数m的取值范围是解得-1≤a≤5,即实数a的取值范围是[-1,5].
5.是否存在实数p,使“4x+p<0”是“(x-2)(x+1)>0”的充分条件?若存在,求出p的取值范围;若不存在,请说明理由.
角度二
二次不等式
解:由(x-2)(x+1)>0得x>2,或x<-1,由4x+p<0得x<-,
若“4x+p<0”是“(x-2)(x+1)>0”的充分条件,
则需满足-≤-1,即p≥4,
故当p≥4时,“4x+p<0”是“(x-2)(x+1)>0”的充分条件.
6.是否存在实数p,使“4x+p<0”是“(x-2)(x+1)>0”的必要条件?若存在,求出p的取值范围;若不存在,请说明理由.
角度二
二次不等式
解:由(x-2)(x+1)>0
4x+p<0,所以不存在实数p使“4x+p<0”是“(x-2)(x+1)>0”的必要条件.
7.已知p:-4角度二
二次不等式
解:由-4又q是p的充分条件,则有{x|2因而需满足解得-1≤a≤6.
8.
若“p:x(x-3)<0”是“q:2x-3角度二
二次不等式
解:得p:0由题意,知p?q,qp,则≥3,解得m≥3.
?
9.已知p:x2-2x-3<0,若-a0)是p的一个必要条件,求实数a的取值范围.
角度二
二次不等式
解:由p:x2-2x-3<0,解得-10).
依题意,得{x|-10).
所以解得a≥2.
故实数a的取值范围是[2,+∞).
10.已知条件p:A={x|x2-(a+1)x+a≤0},条件q:B={x|x2-3x+2≤0},当a为何值时,
(1)p是q的充分不必要条件;
(2)p是q的必要不充分条件;
(3)p是q的充要条件.
角度二
二次不等式
[解析] A={x|x2-(a+1)x+a≤0}={x|(x-1)(x-a)≤0},B={x|x2-3x+2≤0}={x|1≤x≤2},(1)因为p是q的充分不必要条件,所以A?B,而当a=1时,A={1},显然成立,当a>1,A=[1,a],需110.已知条件p:A={x|x2-(a+1)x+a≤0},条件q:B={x|x2-3x+2≤0},当a为何值时,
(1)p是q的充分不必要条件;
(2)p是q的必要不充分条件;
(3)p是q的充要条件.
角度二
二次不等式
(2)因为p是q的必要不充分条件,所以B??A,
故A=[1,a],且a>2,
所以a>2时,p是q的必要不充分条件.
10.已知条件p:A={x|x2-(a+1)x+a≤0},条件q:B={x|x2-3x+2≤0},当a为何值时,
(1)p是q的充分不必要条件;
(2)p是q的必要不充分条件;
(3)p是q的充要条件.
角度二
二次不等式
(3)因为p是q的充要条件,所以A=B,故a=2.
11.已知p:实数x满足x2-4ax+3a2<0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且p是q的充分条件,求a的取值范围.
角度二
二次不等式
[解析] p:由x2-4ax+3a2<0,其中a<0得,3aq:由x2-x-6≤0或x2+2x-8>0,得x<-4或x≥-2.
∵p是q的充分条件,
∴a≤-4或-≤a<0.综上可知a的取值范围是a≤-4或-≤a<0.
12.已知p:-1≤≤3,q:x2-2x+1-m2≤0(m>0),若p是q的必要不充分条件,求实数m的取值范围.
角度二
二次不等式
[解析]
[解析] 由p:-1≤≤3得-2≤x≤10,
由q:x2-2x+1-m2≤0(m>0)得-m≤x-1≤m,
∴1-m≤x≤1+m.
∵p是q的必要不充分条件,
又∵m>0,∴013.已知p:x2-x-2<0,q:x∈(-1,m),且p是q的充分条件,但不是必要条件,则实数m的取值范围是( )
A.m>2
B.m≥2
C.-1D.-1角度二
二次不等式
解析:由x2-x-2<0,得x∈(-1,2).
∵p是q的充分条件,但不是必要条件,
∴(-1,2)?(-1,m),∴m>2.故选A.
14.已知命题,命题,若命题是命题的充分不必要条件,则实数的取值范围是(
)
A.
B.
C.
角度二
二次不等式
解析:由命题得或由命题得或
它们的取值范围分别用集合表示由题意得A?B
解得,又
15.已知集合是函数的定义域,集合是不等式的解集,.若是的充分不必要条件,求的取值范围.
A.
B.
C.
角度二
二次不等式
解:由已知A={x|(x-1)(x-a)≤0},B={x|1≤x≤2}.因为p是q的充分条件,但不是必要条件,所以A?B,而当a=1时,A={1},显然成立;当a>1,A={x|1≤x≤a},则需a<2,故115.已知集合是函数的定义域,集合是不等式的解集,.若是的充分不必要条件,求的取值范围.
A.
B.
C.
角度二
二次不等式
解:由已知A={x|(x-1)(x-a)≤0},B={x|1≤x≤2}.因为p是q的充分条件,但不是必要条件,所以A?B,而当a=1时,A={1},显然成立;当a>1,A={x|1≤x≤a},则需a<2,故1环节三
方程类型
16.
已知条件,条件,且是的充分不必要条件,则实数的值为________
A.
B.
C.
D.
角度一
无限制方程
解析:命题“”是命题“”的充分不必要条件,A?B.故
17.一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是()
A.
ac≤0.
B.
ac<0.
C.
ac>0.
角度二
有限制方程
[解析] 充分性:(由ac<0推证方程有一正根和一负根)
∵ac<0,∴一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0,∴方程一定有两不等实根,设为x1、x2,则x1x2=<0,∴方程的两根异号.即方程ax2+bx+c=0有一正根和一负根.
17.一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是()
A.
ac≤0.
B.
ac<0.
C.
ac>0.
必要性:(由方程有一正根和一负根,推证ac<0),
∵方程有一正根和一负根,设为x1、x2,
则由根与系数的关系得x1x2=<0,即ac<0,
综上可知:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
角度二
有限制方程
18.关于x的方程至少有一个负的实数根的充要条件是().
A.
B.
C.
D.
解析:(1)当时,,解得,符合题意
(2)当时,方程有实数根的充要条件为,
即,所以.
角度二
有限制方程
18.关于x的方程至少有一个负的实数根的充要条件是().
A.
B.
C.
D.
当且时,设方程的两个实数根分别为,,当时,此时方程有一个正实数根,一个负实数根,符合题意;
角度二
有限制方程
18.关于x的方程至少有一个负的实数根的充要条件是().
A.
B.
C.
D.
当时,此时方程有两个负实数根,符合题意.
综上,若关于x的方程至少有一个负的实数根,则,反之,若,则关于x的方程至少有个负的实数根.
故关于x的方程至少有一个负的实数根的充要条件是.
角度二
有限制方程
19.已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=?”是假命题,求实数m的取值范围.
A.
B.
C.
D.
[解析] 因为“A∩B=?”是假命题,所以A∩B≠?.设全集U={m|Δ=(-4m)2-4(2m+6)≥0},则U=.
角度二
有限制方程
19.已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=?”是假命题,求实数m的取值范围.
A.
B.
C.
D.
假设方程x2-4mx+2m+6=0的两根x1,x2均非负,
解得m≥.
角度二
有限制方程
19.已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=?”是假命题,求实数m的取值范围.
A.
B.
C.
D.
又集合关于全集U的补集是{m|m≤-1}.
所以实数m的取值范围是(-∞,-1].
角度二
有限制方程
20.
已知方程x2-2(m+2)x+m2-1=0有两个大于2的根,试求实数m的取值范围.
A.
B.
C.
D.
由于方程x2-2(m+2)x+m2-1=0有两个大于2的根,设这两个根为x1、x2,则有。结合,解得m>5.所以m的取值范围为(5,+∞).
这里属凑韦达法,不最最佳方法,后面专讲图像法
角度二
有限制方程
21.设m∈N+,一元二次方程x2-4x+m=0有整数根的充要条件是m=(
)?
A.3
B.4
C.3,4
D-3,-4
解析:由题知,x==2±,因为x是整数,即2±为整数,所以为整数,且m≤4,又m∈N+,取m=1,2,3,4.验证可得m=3,4符合题意,所以m=3,4时可以推出一元二次方程x2-4x+m=0有整数根.
角度二
有限制方程
谢谢观看
充要条件求参题型大全
课件制作
胡琪
1.2常用逻辑用语复习
北师大(2019)必修1
看看这一节我们要学什么
1.根据不等式之间的充分必要关系求参.
2.根据方程之间的充分必要关系求参.
环节一
小推大
有一个圆A,在其内又含有一个圆B.请回答:
1.“点在A内”是“点在B内”的什么条件?
由已知B?A,所以点在B内,能推出点在A内,故“点在A内”是“点在B内”的必要条件.
2.“点在B内”是“点在A内”的什么条件?
因为点在B内?点一定在A内,所以“点在B内”是“点在A内”的充分条件.
X>0
X>1
X>2
X>3
X>4
试举一充分条件的例子
x<3
X<5
X<8
X<10
X<6
B
A
在A中的元素就一定在B中,但在B中的元素不一定在A中。
?
小推大原理
如果一个命题的条件和结论可以用集合表示且这两个集合有大小关系,那么,代表小集合的一方一定能推出代表大集合的一方,而大的不能推出小的,结合充分必要的定义,就可以方便地判断条件的类型。这种方法叫【集合法】
环节二
不等式类型
1.已知p:2x+m>0,q:x-4>0,若p是q的充分条件,则实数m的取值范围是?
A.
角度一
一次不等式
[解析] p:x>-,q:x>4,若p是q的充要条件,∴-≥4,∴m≤-8.
2.已知,,若是的必要不充分条件,则实数a的取值范围是
A.
B.
C.
角度一
一次不等式
因为或,或,且是的必要不充分条件,所以或?{或}
2.已知,,若是的必要不充分条件,则实数a的取值范围是
A.
B.
C.
角度一
一次不等式
所以或解得.
故实数a的取值范围是.
3.已知集合P={x|a-4
角度一
一次不等式
解:因为“x∈P”是x∈Q的必要条件,所以Q?P.
所以{x|1
4.已知集合A=,B={x|x≥m+1或x≤m-1},命题
p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数
m的取值范围.
A.
B.
C.
角度一
一次不等式
解:因为命题p是命题q的充分条件,所以A?B.所以m+1≤,或m-1≥2,解得m≤-,或m≥3.故实数m的取值范围是解得-1≤a≤5,即实数a的取值范围是[-1,5].
5.是否存在实数p,使“4x+p<0”是“(x-2)(x+1)>0”的充分条件?若存在,求出p的取值范围;若不存在,请说明理由.
角度二
二次不等式
解:由(x-2)(x+1)>0得x>2,或x<-1,由4x+p<0得x<-,
若“4x+p<0”是“(x-2)(x+1)>0”的充分条件,
则需满足-≤-1,即p≥4,
故当p≥4时,“4x+p<0”是“(x-2)(x+1)>0”的充分条件.
6.是否存在实数p,使“4x+p<0”是“(x-2)(x+1)>0”的必要条件?若存在,求出p的取值范围;若不存在,请说明理由.
角度二
二次不等式
解:由(x-2)(x+1)>0
4x+p<0,所以不存在实数p使“4x+p<0”是“(x-2)(x+1)>0”的必要条件.
7.已知p:-4
二次不等式
解:由-4
8.
若“p:x(x-3)<0”是“q:2x-3
二次不等式
解:得p:0
?
9.已知p:x2-2x-3<0,若-a
角度二
二次不等式
解:由p:x2-2x-3<0,解得-1
依题意,得{x|-1
所以解得a≥2.
故实数a的取值范围是[2,+∞).
10.已知条件p:A={x|x2-(a+1)x+a≤0},条件q:B={x|x2-3x+2≤0},当a为何值时,
(1)p是q的充分不必要条件;
(2)p是q的必要不充分条件;
(3)p是q的充要条件.
角度二
二次不等式
[解析] A={x|x2-(a+1)x+a≤0}={x|(x-1)(x-a)≤0},B={x|x2-3x+2≤0}={x|1≤x≤2},(1)因为p是q的充分不必要条件,所以A?B,而当a=1时,A={1},显然成立,当a>1,A=[1,a],需1
(1)p是q的充分不必要条件;
(2)p是q的必要不充分条件;
(3)p是q的充要条件.
角度二
二次不等式
(2)因为p是q的必要不充分条件,所以B??A,
故A=[1,a],且a>2,
所以a>2时,p是q的必要不充分条件.
10.已知条件p:A={x|x2-(a+1)x+a≤0},条件q:B={x|x2-3x+2≤0},当a为何值时,
(1)p是q的充分不必要条件;
(2)p是q的必要不充分条件;
(3)p是q的充要条件.
角度二
二次不等式
(3)因为p是q的充要条件,所以A=B,故a=2.
11.已知p:实数x满足x2-4ax+3a2<0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且p是q的充分条件,求a的取值范围.
角度二
二次不等式
[解析] p:由x2-4ax+3a2<0,其中a<0得,3a
∵p是q的充分条件,
∴a≤-4或-≤a<0.综上可知a的取值范围是a≤-4或-≤a<0.
12.已知p:-1≤≤3,q:x2-2x+1-m2≤0(m>0),若p是q的必要不充分条件,求实数m的取值范围.
角度二
二次不等式
[解析]
[解析] 由p:-1≤≤3得-2≤x≤10,
由q:x2-2x+1-m2≤0(m>0)得-m≤x-1≤m,
∴1-m≤x≤1+m.
∵p是q的必要不充分条件,
又∵m>0,∴0
A.m>2
B.m≥2
C.-1
二次不等式
解析:由x2-x-2<0,得x∈(-1,2).
∵p是q的充分条件,但不是必要条件,
∴(-1,2)?(-1,m),∴m>2.故选A.
14.已知命题,命题,若命题是命题的充分不必要条件,则实数的取值范围是(
)
A.
B.
C.
角度二
二次不等式
解析:由命题得或由命题得或
它们的取值范围分别用集合表示由题意得A?B
解得,又
15.已知集合是函数的定义域,集合是不等式的解集,.若是的充分不必要条件,求的取值范围.
A.
B.
C.
角度二
二次不等式
解:由已知A={x|(x-1)(x-a)≤0},B={x|1≤x≤2}.因为p是q的充分条件,但不是必要条件,所以A?B,而当a=1时,A={1},显然成立;当a>1,A={x|1≤x≤a},则需a<2,故1
A.
B.
C.
角度二
二次不等式
解:由已知A={x|(x-1)(x-a)≤0},B={x|1≤x≤2}.因为p是q的充分条件,但不是必要条件,所以A?B,而当a=1时,A={1},显然成立;当a>1,A={x|1≤x≤a},则需a<2,故1
方程类型
16.
已知条件,条件,且是的充分不必要条件,则实数的值为________
A.
B.
C.
D.
角度一
无限制方程
解析:命题“”是命题“”的充分不必要条件,A?B.故
17.一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是()
A.
ac≤0.
B.
ac<0.
C.
ac>0.
角度二
有限制方程
[解析] 充分性:(由ac<0推证方程有一正根和一负根)
∵ac<0,∴一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0,∴方程一定有两不等实根,设为x1、x2,则x1x2=<0,∴方程的两根异号.即方程ax2+bx+c=0有一正根和一负根.
17.一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是()
A.
ac≤0.
B.
ac<0.
C.
ac>0.
必要性:(由方程有一正根和一负根,推证ac<0),
∵方程有一正根和一负根,设为x1、x2,
则由根与系数的关系得x1x2=<0,即ac<0,
综上可知:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
角度二
有限制方程
18.关于x的方程至少有一个负的实数根的充要条件是().
A.
B.
C.
D.
解析:(1)当时,,解得,符合题意
(2)当时,方程有实数根的充要条件为,
即,所以.
角度二
有限制方程
18.关于x的方程至少有一个负的实数根的充要条件是().
A.
B.
C.
D.
当且时,设方程的两个实数根分别为,,当时,此时方程有一个正实数根,一个负实数根,符合题意;
角度二
有限制方程
18.关于x的方程至少有一个负的实数根的充要条件是().
A.
B.
C.
D.
当时,此时方程有两个负实数根,符合题意.
综上,若关于x的方程至少有一个负的实数根,则,反之,若,则关于x的方程至少有个负的实数根.
故关于x的方程至少有一个负的实数根的充要条件是.
角度二
有限制方程
19.已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=?”是假命题,求实数m的取值范围.
A.
B.
C.
D.
[解析] 因为“A∩B=?”是假命题,所以A∩B≠?.设全集U={m|Δ=(-4m)2-4(2m+6)≥0},则U=.
角度二
有限制方程
19.已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=?”是假命题,求实数m的取值范围.
A.
B.
C.
D.
假设方程x2-4mx+2m+6=0的两根x1,x2均非负,
解得m≥.
角度二
有限制方程
19.已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=?”是假命题,求实数m的取值范围.
A.
B.
C.
D.
又集合关于全集U的补集是{m|m≤-1}.
所以实数m的取值范围是(-∞,-1].
角度二
有限制方程
20.
已知方程x2-2(m+2)x+m2-1=0有两个大于2的根,试求实数m的取值范围.
A.
B.
C.
D.
由于方程x2-2(m+2)x+m2-1=0有两个大于2的根,设这两个根为x1、x2,则有。结合,解得m>5.所以m的取值范围为(5,+∞).
这里属凑韦达法,不最最佳方法,后面专讲图像法
角度二
有限制方程
21.设m∈N+,一元二次方程x2-4x+m=0有整数根的充要条件是m=(
)?
A.3
B.4
C.3,4
D-3,-4
解析:由题知,x==2±,因为x是整数,即2±为整数,所以为整数,且m≤4,又m∈N+,取m=1,2,3,4.验证可得m=3,4符合题意,所以m=3,4时可以推出一元二次方程x2-4x+m=0有整数根.
角度二
有限制方程
谢谢观看
