2021-2022学年高一数学人教A版必修五第一章解三角形1.1.2 余弦定理 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年高一数学人教A版必修五第一章解三角形1.1.2 余弦定理 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 193.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
1.1.2余弦定理
教学目标
1.掌握余弦定理的证明方法,把握余弦定理及其推论,能够运用余弦定理解决两类基本的解三角形问题。
2.培养学生在方程思想指导下处理解三角形问题的运算能力;通过三角函数、余弦定理、向量的数量积等知识间的关系,培养学生的数学运算和逻辑素养。
已知三角形的两角和任意一边,
或者是已知两边和其中一边的对角。(注意解的个数)
一.复习回顾
正弦定理:
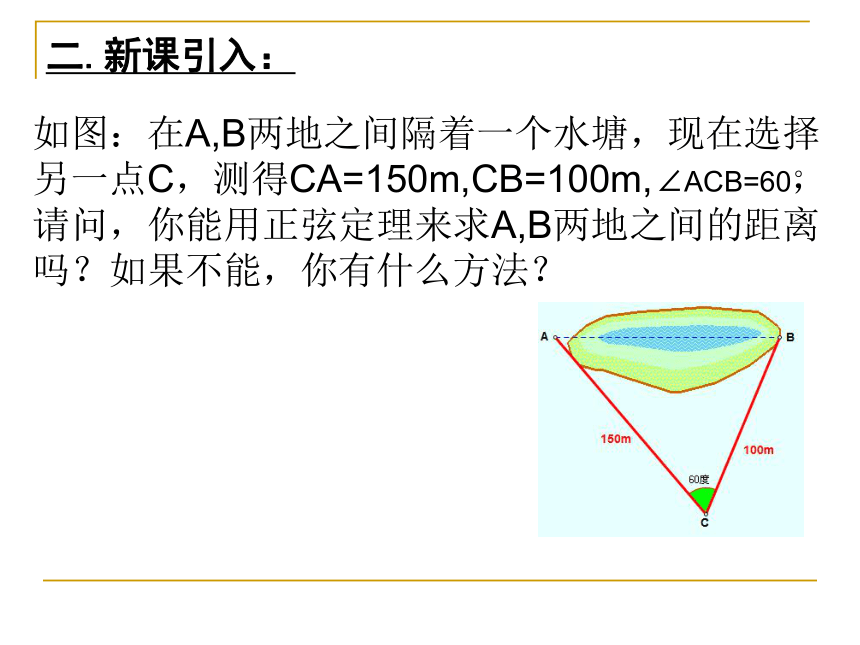
二.新课引入:
如图:在A,B两地之间隔着一个水塘,现在选择
另一点C,测得CA=150m,CB=100m,
,
请问,你能用正弦定理来求A,B两地之间的距离
吗?如果不能,你有什么方法?
∠ACB=60°
c=
?
三.探索(建模):
已知两边及夹角求解三角形△ABC为任意三角形,已知BC=a,AC=b及∠C,求AB边长c.
向量法:
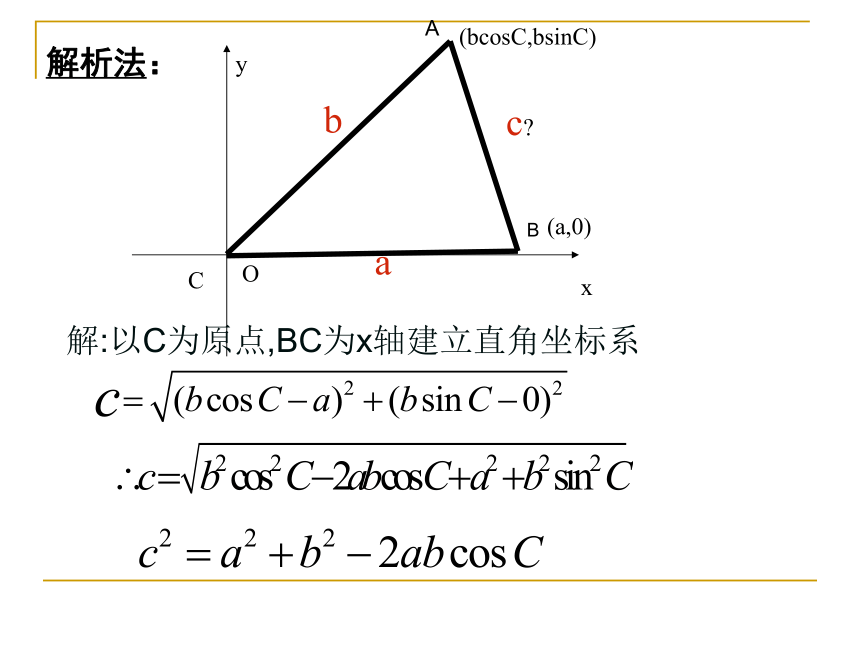
解析法:
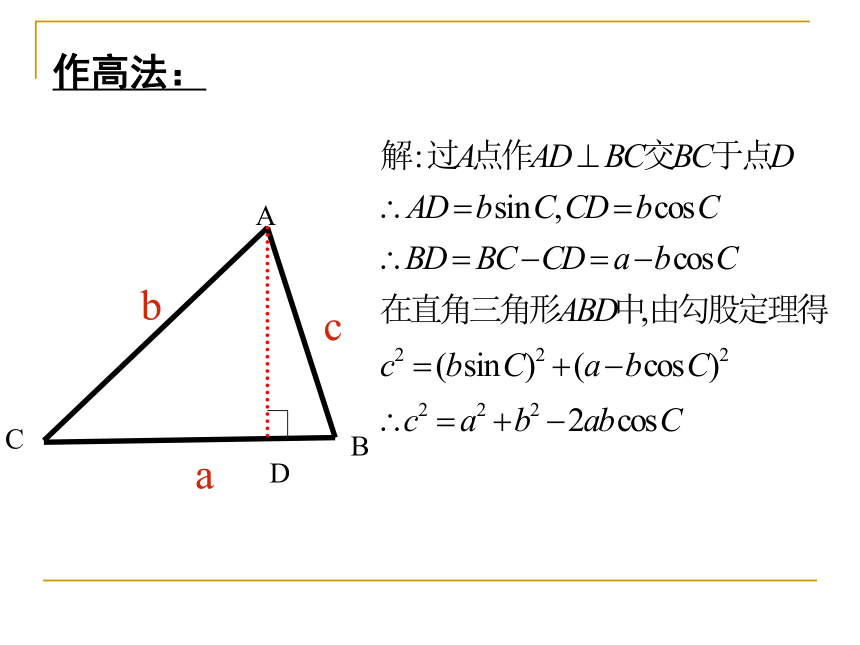
作高法:
同理可证:
向量法:
A
B
C
c
b
a
(bcosC,bsinC)
(a,0)
C
x
a
y
O
解析法:
b
c?
A
B
解:以C为原点,BC为x轴建立直角坐标系
A
B
C
D
a
b
c
作高法:
用语言描述:
三角形任何一边的平方等于其它两边的平方和,
再减去这两边与它们夹角的余弦的积的两倍。
余弦定理:
已知a、b、c(三边),可以求什么?
四:剖析定理:
五:应用
1.已知两边和它们的夹角,求第三边,进而还可求其它两个角。
,
例1在△ABC中,已知B=450,
,解三角形
思考:你现在能解决这节课开始时我们提出的
问题了吗?
分析:已知三边,求三个角,可用余弦定理的变形来解决问题
2.已知三边,求三个角
例2、在三角形中,已知
,
,
,
求
3.利用余弦定理判断三角形的形状
练习:
1、在三角形ABC中,
总结:
1.余弦定理适用于任何三角形
3.由余弦定理可知:边角的转换
2.利用余弦定理解三角形:
(1).已知三边
(2).已知两边及这两边的夹角
《余弦定理》说课稿
一、说教材
1、教材的地位和作用
本节课是人教A版必修五第一章第一节第二小节的内容,它是在学生已经学习了正弦定理的内容,初步掌握了正弦定理的证明及应用的基础上进行学习的。通过利用平面几何法、坐标法(两点的距离公式)、向量的模等方法推导余弦定理,学生会正确理解余弦定理的结构特征和表现形式,解决“边、角、边”和“边、边、边”问题,体会方程思想,理解余弦定理是勾股定理的特例,
从多视角思考问题和发现问题,形成良好的思维品质,激发学生探究数学,应用数学的潜能,培养学生思维的广阔性。
2、教学目标
1.掌握余弦定理的两组表示形式及证明余弦定理的方法,深化与细化方程思想,理解余弦定理的本质,并会运用余弦定理解决两类基本的解三角形问题。
2.培养学生在方程思想指导下处理解三角形问题的运算能力;通过三角函数、余弦定理、向量的数量积等知识间的关系,培养学生的数学运算和逻辑素养。
3、教学重难点
教学重点是余弦定理的发现过程及定理的应用;
教学难点是余弦定理的推导方法过程及余弦定
理在应用求解三角形时的思路。
二、说教法学法
1、学情分析
本课之前,学生已经学习了三角函数、向量基本知识和正弦定理有关内容,对于三角形中的边角关系有了较进一步的认识。在此基础上利用向量方法探求余弦定理,学生已有一定的学习基础和学习兴趣。总体上学生应用数学知识的意识不强,创造力较弱,看待与分析问题不深入,知识的系统性不完善,使得学生在余弦定理推导方法的探求上有一定的难度,在发掘出余弦定理的结构特征、表现形式的数学美时,能够激发学生热爱数学的思想感情;从具体问题中抽象出数学的本质,应用方程的思想去审视,解决问题是学生学习的一大难点。
2、教法学法分析
在新课标的理念下,教师是学生学习的引导者、组织者、合作者和参与者.基于本节课的特点,我采用探究式和讲授式的教学方法.
在教师的引导下学生以自主探索、合作交流的方式进行学习.
体现数学逻辑推理的核心素养
三、教学过程
1.导入
2.讲述新课:余弦定理的推导
应用
3.练习
4.小结
5.布置作业
1.1.2余弦定理
教学目标
1.掌握余弦定理的证明方法,把握余弦定理及其推论,能够运用余弦定理解决两类基本的解三角形问题。
2.培养学生在方程思想指导下处理解三角形问题的运算能力;通过三角函数、余弦定理、向量的数量积等知识间的关系,培养学生的数学运算和逻辑素养。
已知三角形的两角和任意一边,
或者是已知两边和其中一边的对角。(注意解的个数)
一.复习回顾
正弦定理:
二.新课引入:
如图:在A,B两地之间隔着一个水塘,现在选择
另一点C,测得CA=150m,CB=100m,
,
请问,你能用正弦定理来求A,B两地之间的距离
吗?如果不能,你有什么方法?
∠ACB=60°
c=
?
三.探索(建模):
已知两边及夹角求解三角形△ABC为任意三角形,已知BC=a,AC=b及∠C,求AB边长c.
向量法:
解析法:
作高法:
同理可证:
向量法:
A
B
C
c
b
a
(bcosC,bsinC)
(a,0)
C
x
a
y
O
解析法:
b
c?
A
B
解:以C为原点,BC为x轴建立直角坐标系
A
B
C
D
a
b
c
作高法:
用语言描述:
三角形任何一边的平方等于其它两边的平方和,
再减去这两边与它们夹角的余弦的积的两倍。
余弦定理:
已知a、b、c(三边),可以求什么?
四:剖析定理:
五:应用
1.已知两边和它们的夹角,求第三边,进而还可求其它两个角。
,
例1在△ABC中,已知B=450,
,解三角形
思考:你现在能解决这节课开始时我们提出的
问题了吗?
分析:已知三边,求三个角,可用余弦定理的变形来解决问题
2.已知三边,求三个角
例2、在三角形中,已知
,
,
,
求
3.利用余弦定理判断三角形的形状
练习:
1、在三角形ABC中,
总结:
1.余弦定理适用于任何三角形
3.由余弦定理可知:边角的转换
2.利用余弦定理解三角形:
(1).已知三边
(2).已知两边及这两边的夹角
《余弦定理》说课稿
一、说教材
1、教材的地位和作用
本节课是人教A版必修五第一章第一节第二小节的内容,它是在学生已经学习了正弦定理的内容,初步掌握了正弦定理的证明及应用的基础上进行学习的。通过利用平面几何法、坐标法(两点的距离公式)、向量的模等方法推导余弦定理,学生会正确理解余弦定理的结构特征和表现形式,解决“边、角、边”和“边、边、边”问题,体会方程思想,理解余弦定理是勾股定理的特例,
从多视角思考问题和发现问题,形成良好的思维品质,激发学生探究数学,应用数学的潜能,培养学生思维的广阔性。
2、教学目标
1.掌握余弦定理的两组表示形式及证明余弦定理的方法,深化与细化方程思想,理解余弦定理的本质,并会运用余弦定理解决两类基本的解三角形问题。
2.培养学生在方程思想指导下处理解三角形问题的运算能力;通过三角函数、余弦定理、向量的数量积等知识间的关系,培养学生的数学运算和逻辑素养。
3、教学重难点
教学重点是余弦定理的发现过程及定理的应用;
教学难点是余弦定理的推导方法过程及余弦定
理在应用求解三角形时的思路。
二、说教法学法
1、学情分析
本课之前,学生已经学习了三角函数、向量基本知识和正弦定理有关内容,对于三角形中的边角关系有了较进一步的认识。在此基础上利用向量方法探求余弦定理,学生已有一定的学习基础和学习兴趣。总体上学生应用数学知识的意识不强,创造力较弱,看待与分析问题不深入,知识的系统性不完善,使得学生在余弦定理推导方法的探求上有一定的难度,在发掘出余弦定理的结构特征、表现形式的数学美时,能够激发学生热爱数学的思想感情;从具体问题中抽象出数学的本质,应用方程的思想去审视,解决问题是学生学习的一大难点。
2、教法学法分析
在新课标的理念下,教师是学生学习的引导者、组织者、合作者和参与者.基于本节课的特点,我采用探究式和讲授式的教学方法.
在教师的引导下学生以自主探索、合作交流的方式进行学习.
体现数学逻辑推理的核心素养
三、教学过程
1.导入
2.讲述新课:余弦定理的推导
应用
3.练习
4.小结
5.布置作业
