2021-2022人教版八年级上册数学第十一章 三角形复习课件(20张)
文档属性
| 名称 | 2021-2022人教版八年级上册数学第十一章 三角形复习课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第十一章
小结与复习
课件说明
本章中学生学习了与三角形有关的线段(边、高、
中线、角平分线)和角(内角、外角),探索并证
明了三角形两边的和大于第三边以及三角形内角和
定理,在此基础上研究了多边形的有关线段(边、
对角线)和角(内角、外角),并证明了多边形内
角和与外角和公式.本节课对本章内容进行梳理总
结,建立知识体系,综合运用本章知识解决问题.
课件说明
学习目标:
1.复习本章内容,整理本章知识,形成知识体系,
体会研究几何问题的思路和方法.
2.进一步发展推理能力,能够有条理地思考、解决
问题.
学习重点:
复习本章内容并运用它们进行有关的计算与证明,
构建本章知识结构.
问题1
请同学们回答下列问题:
(1)三角形的三边之间有怎样的关系?得出这个结论
的依据是什么?
(2)三角形的三个内角之间有怎样的关系?如何证明
这个结论?
问题1
请同学们回答下列问题:
(3)直角三角形的两个锐角之间有怎样的关系?三角
形的一个外角和它不相邻的两个内角之间有怎样
的关系?这些结论能由三角形内角和定理得出吗?
(4)n
边形的n
个内角有怎样的关系?如何推出这个
结论?
(5)n
边形的外角和与n
有关吗?为什么?
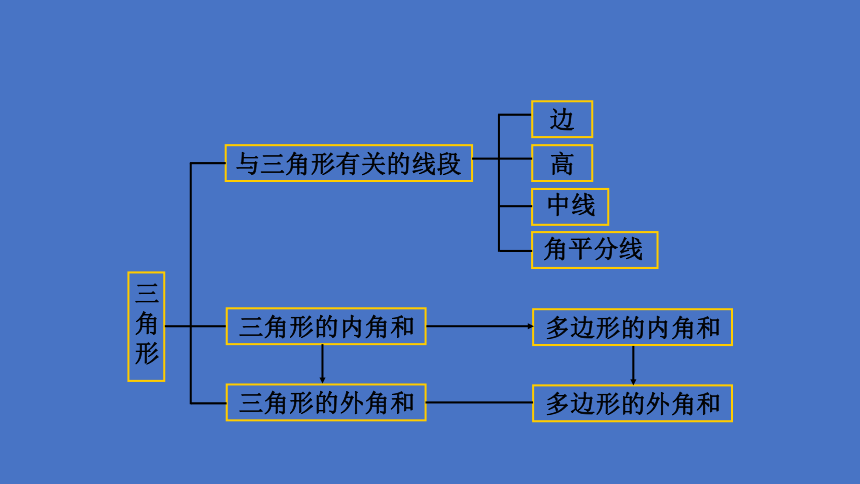
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
A
组 复习与三角形有关的线段:
1.若三角形的两边分别为3
和5
,则第三边长m
的取值
范围是__________.
2
<
m
<
8
A
组 复习与三角形有关的线段:
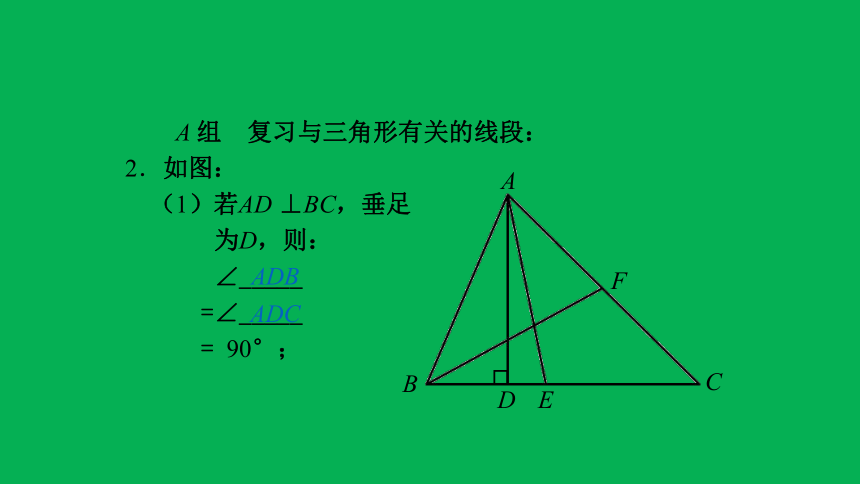
2.如图:
(1)若AD
⊥BC,垂足
为D,则:
∠_____
=∠_____
=
90°;
ADB
ADC
A
B
C
D
E
F
A
组 复习与三角形有关的线段:
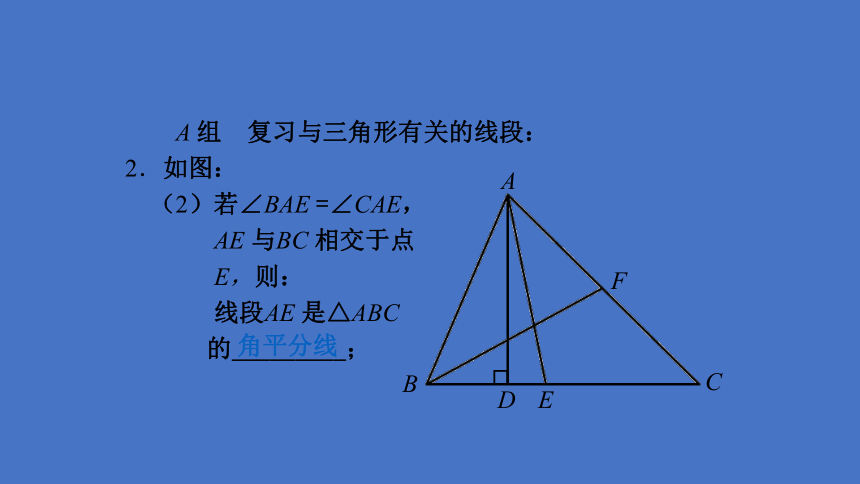
2.如图:
(2)若∠BAE
=∠CAE,
AE
与BC
相交于点
E,则:
线段AE
是△ABC
的_________;
角平分线
A
B
C
D
E
F
A
组 复习与三角形有关的线段:
2.如图:
(3)若AF
=CF,BF
与
AC
相交于点F,
则:△ABC
的中
线是
.
BF
A
B
C
D
E
F
B
组 巩固与三角形有关的角:
如图,在△ABC
中,∠BAC
=80°,∠ABC
=60°.
(1)∠C
= ;
(2)若AE
是△ABC
的
角平分线,则:
∠AEC
=
;
(3)若BF
是△ABC
的
高,与角平分线
AE
相交于点O,则∠EOF
= .
40°
100°
130°
A
B
C
O
E
F
例1
已知等腰三角形的两边长分别为10
和6
,则
三角形的周长是 .
变式1 若等腰三角形的周长为20,一边长为4,
则其他两边长为 .
22或26
8和8
变式2 小明用一条长20
cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:设较短的边长为
x
cm,则较长的边长为2x
cm.
若较短的边为腰,则x
+
x
+
2x
=20.
解得 x
=5.
即 2x
=10.
因为
5
+
5
=10,不符合三角形两边的和大于第
三边,所以不能围成腰长5
cm的等腰三角形.
变式2 小明用一条长20
cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:若较长的边为腰,则
x
+
2x
+
2x
=20.
解得 x
=4.
所以,这个三角形的三边分别为:
4
cm,
8
cm,
8
cm.
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平
分线BD,CE
交于点O.
若∠ABC
=40°,∠ACB
=60°,则:
∠BOC
=
.
A
B
C
O
E
D
130°
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平
分线BD,CE
交于点O.
变式1 若∠A
=80°,则∠BOC
=
.
变式2 你能猜想出∠BOC
与∠A
之间的数量关系吗?
130°
∠BOC
=
90°+
∠A
A
B
C
O
E
D
A
B
C
O
E
D
变式3 如图,若换成两
外角平分线相交于O,则
∠BOC
与∠A
又有怎样的数
量关系?
∠BOC
=
90°-
∠A
变式4 如图,若换成一内角与一外角平分线相交
于点O,则∠BOC与∠A
又有怎样的数量关系?
∠BOC
=
∠A
A
B
C
O
E
D
变式5 如图,若换成两条高相交于点O,
∠A
与
∠BOC
又有怎样的数量关系?
∠BOC
=
180°
-∠A
A
B
C
O
E
D
(1)本章的核心知识有哪些?这些知识间有什么样
的联系?
(2)通过本节课的复习,你能说说三角形内角和定
理的由来及作用吗?
课堂小结
第十一章
小结与复习
课件说明
本章中学生学习了与三角形有关的线段(边、高、
中线、角平分线)和角(内角、外角),探索并证
明了三角形两边的和大于第三边以及三角形内角和
定理,在此基础上研究了多边形的有关线段(边、
对角线)和角(内角、外角),并证明了多边形内
角和与外角和公式.本节课对本章内容进行梳理总
结,建立知识体系,综合运用本章知识解决问题.
课件说明
学习目标:
1.复习本章内容,整理本章知识,形成知识体系,
体会研究几何问题的思路和方法.
2.进一步发展推理能力,能够有条理地思考、解决
问题.
学习重点:
复习本章内容并运用它们进行有关的计算与证明,
构建本章知识结构.
问题1
请同学们回答下列问题:
(1)三角形的三边之间有怎样的关系?得出这个结论
的依据是什么?
(2)三角形的三个内角之间有怎样的关系?如何证明
这个结论?
问题1
请同学们回答下列问题:
(3)直角三角形的两个锐角之间有怎样的关系?三角
形的一个外角和它不相邻的两个内角之间有怎样
的关系?这些结论能由三角形内角和定理得出吗?
(4)n
边形的n
个内角有怎样的关系?如何推出这个
结论?
(5)n
边形的外角和与n
有关吗?为什么?
边
高
中线
角平分线
多边形的内角和
多边形的外角和
与三角形有关的线段
三
角
形
三角形的内角和
三角形的外角和
A
组 复习与三角形有关的线段:
1.若三角形的两边分别为3
和5
,则第三边长m
的取值
范围是__________.
2
<
m
<
8
A
组 复习与三角形有关的线段:
2.如图:
(1)若AD
⊥BC,垂足
为D,则:
∠_____
=∠_____
=
90°;
ADB
ADC
A
B
C
D
E
F
A
组 复习与三角形有关的线段:
2.如图:
(2)若∠BAE
=∠CAE,
AE
与BC
相交于点
E,则:
线段AE
是△ABC
的_________;
角平分线
A
B
C
D
E
F
A
组 复习与三角形有关的线段:
2.如图:
(3)若AF
=CF,BF
与
AC
相交于点F,
则:△ABC
的中
线是
.
BF
A
B
C
D
E
F
B
组 巩固与三角形有关的角:
如图,在△ABC
中,∠BAC
=80°,∠ABC
=60°.
(1)∠C
= ;
(2)若AE
是△ABC
的
角平分线,则:
∠AEC
=
;
(3)若BF
是△ABC
的
高,与角平分线
AE
相交于点O,则∠EOF
= .
40°
100°
130°
A
B
C
O
E
F
例1
已知等腰三角形的两边长分别为10
和6
,则
三角形的周长是 .
变式1 若等腰三角形的周长为20,一边长为4,
则其他两边长为 .
22或26
8和8
变式2 小明用一条长20
cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:设较短的边长为
x
cm,则较长的边长为2x
cm.
若较短的边为腰,则x
+
x
+
2x
=20.
解得 x
=5.
即 2x
=10.
因为
5
+
5
=10,不符合三角形两边的和大于第
三边,所以不能围成腰长5
cm的等腰三角形.
变式2 小明用一条长20
cm的细绳围成了一个等腰
三角形,他想使这个三角形的一边长是另一边长的2倍,
那么这个三角形的各边的长分别是多少?
解:若较长的边为腰,则
x
+
2x
+
2x
=20.
解得 x
=4.
所以,这个三角形的三边分别为:
4
cm,
8
cm,
8
cm.
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平
分线BD,CE
交于点O.
若∠ABC
=40°,∠ACB
=60°,则:
∠BOC
=
.
A
B
C
O
E
D
130°
例2 如图,在△ABC
中,∠
ABC
,∠
ACB
的平
分线BD,CE
交于点O.
变式1 若∠A
=80°,则∠BOC
=
.
变式2 你能猜想出∠BOC
与∠A
之间的数量关系吗?
130°
∠BOC
=
90°+
∠A
A
B
C
O
E
D
A
B
C
O
E
D
变式3 如图,若换成两
外角平分线相交于O,则
∠BOC
与∠A
又有怎样的数
量关系?
∠BOC
=
90°-
∠A
变式4 如图,若换成一内角与一外角平分线相交
于点O,则∠BOC与∠A
又有怎样的数量关系?
∠BOC
=
∠A
A
B
C
O
E
D
变式5 如图,若换成两条高相交于点O,
∠A
与
∠BOC
又有怎样的数量关系?
∠BOC
=
180°
-∠A
A
B
C
O
E
D
(1)本章的核心知识有哪些?这些知识间有什么样
的联系?
(2)通过本节课的复习,你能说说三角形内角和定
理的由来及作用吗?
课堂小结
