25.2用列举法求概率(第1课时) 课件(共26张PPT)
文档属性
| 名称 | 25.2用列举法求概率(第1课时) 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
25.2
用列举法求概率
---第1课时
人教版
九年级上
教学目标
1.掌握“直接列举法”和“列表法”.
2.学会用“列表”表示出所有可能出现的结果.(难点)
3.熟练利用“列表法”求随机事件的概率.(重点)
回顾旧知
回答下列问题,并说明理由.
(1)掷一枚硬币,正面向上的概率是_______;
(2)袋子中装有
5
个红球,3
个绿球,这些球除了颜色外都相同,从袋子中随机摸出一个球,它是红色的概率为________;
(3)掷一个骰子,观察向上一面的点数,点数大于
4
的概率为
______.
情景导入
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
我们一起来做游戏
合作探究
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
①
②
探究一:直接列举法
合作探究
“掷两枚硬币”所有结果如下:
正
正
正
反
反
正
反
反
①
②
①
②
①
②
①
②
合作探究
解:
(1)
两枚硬币两面一样包括两面都是正面,两面都是反面,共两种情形,所以学生赢的概率是
(2)
一枚硬币正面朝上,一枚硬币反面朝上,共有反正,正反两种情形,所以老师赢的概率是
∵P(学生赢)
=
P(老师赢),
∴这个游戏是公平的.
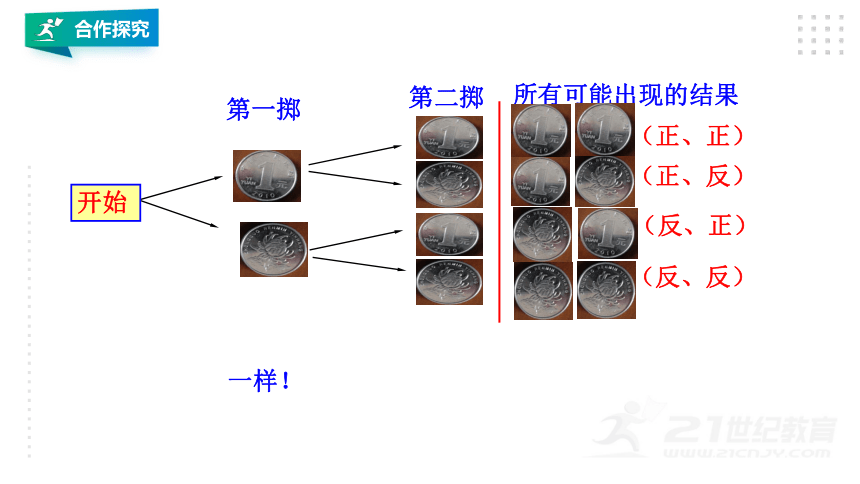
思考1:“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
合作探究
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
一样!
合作探究
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
知识点拨:直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法.
趁热打铁
1、如果从长度分别为2、4、6、7的四条线段中随机抽取三条线段,求抽取的三条线段能构成三角形的概率.
解:从长度分别为2、4、6、7的四条线段中随机抽取三条线段,它们为2,4,6;2,4,7;2,6,7;4,6,7,共有4种等可能的结果,
其中三条线段能构成三角形的有2种结果,
所以三条线段能构成三角形的概率为
合作探究
探究一:列表法
同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)
两个骰子的点数相同;
(2)
两个骰子点数的和是9;
(3)
至少有一个骰子的点数为2.
分析:当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
如何列表呢?
合作探究
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
合作探究
把两个骰子分别标记为第1个和第2个,列表如下:
第
一
个
第
二
个
注意有序数对要统一顺序
合作探究
解:由列表得,同时掷两枚骰子,可能出现的结果有36个,它们出现的可能性相等.
满足两枚骰子的点数相同(记为事件A)的结果有6个,则
P(A)=
;
(2)
满足两枚骰子的点数之和是9(记为事件B)的结果有4个,则P(B)=
;
(3)
满足至少有一枚骰子的点数为2(记为事件C)的结果有11个,则P(C)=
.
思考2:“同时掷两枚质地均匀的骰子”与“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
没变化!
趁热打铁
1、一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
趁热打铁
结果
第一次
第二次
解:利用表格列出所有等可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
由上表可以看出,摸两次球可能出现的结果有9种,其中两次摸出的都是红球的结果有4种,所以:
趁热打铁
变式训练:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
合作探究
(1)用列表法求概率适用于事件中涉及两个因素,并且可能出现的
结果数目较多;
(2)在运用列表法求概率时,应注意各种结果出现的可能性相等,
要注意列表的顺序,并不重不漏地列出所有可能的结果.
第一步:列表格;
第二步:在所有可能情况n中,再找到满足条件的事件的个数m;
第三步:代入概率公式
计算事件的概率.
1.列表法求概率应注意的问题:
归纳总结:
2.列表法求概率的基本步骤:
综合演练
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是(
)
2.某次考试中,每道单项选择题有4个选项,某同学有两道单项选择题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是(
)
B
D
A.
B.
C.
D.
A.
B.
C.
D.
综合演练
3.某校组织九年级学生参加中考体育测试,共租3辆客车,分别编号为1、2、3,李军和赵娟两人可任选一辆车乘坐,则两人同坐2号车的概率为( )
A
.
B.
C.
D.
A
4.如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是(
)
A.
B.
C.
D.
B
综合演练
5.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)
摸出两张牌的数字之和为4的概率为多少?
(2)
摸出为两张牌的数字相等的概率为多少?
综合演练
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:下表列出了所有可能出现的结果,共9种.
能力提升
6、在6张卡片上分别写有1-6的整数,随机地抽取一张后不放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
1
2
3
4
5
6
1
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
第
一
张
第
二
张
能力提升
解:由列表得,两次抽取卡片后,可能出现的结果有30个,它们出现的可能性相等.
P(A)
=
=
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有8个,则
课堂总结
说一说:
1、本节课我们学习了几种列举法?分别是什么?
2、它们的适用对象满足什么条件?分别有哪些步骤?
本节课你有哪些收获?
作业布置
习题25.2
P139页:1、2、3
https://www.21cnjy.com/help/help_extract.php
25.2
用列举法求概率
---第1课时
人教版
九年级上
教学目标
1.掌握“直接列举法”和“列表法”.
2.学会用“列表”表示出所有可能出现的结果.(难点)
3.熟练利用“列表法”求随机事件的概率.(重点)
回顾旧知
回答下列问题,并说明理由.
(1)掷一枚硬币,正面向上的概率是_______;
(2)袋子中装有
5
个红球,3
个绿球,这些球除了颜色外都相同,从袋子中随机摸出一个球,它是红色的概率为________;
(3)掷一个骰子,观察向上一面的点数,点数大于
4
的概率为
______.
情景导入
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
我们一起来做游戏
合作探究
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
①
②
探究一:直接列举法
合作探究
“掷两枚硬币”所有结果如下:
正
正
正
反
反
正
反
反
①
②
①
②
①
②
①
②
合作探究
解:
(1)
两枚硬币两面一样包括两面都是正面,两面都是反面,共两种情形,所以学生赢的概率是
(2)
一枚硬币正面朝上,一枚硬币反面朝上,共有反正,正反两种情形,所以老师赢的概率是
∵P(学生赢)
=
P(老师赢),
∴这个游戏是公平的.
思考1:“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
合作探究
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
一样!
合作探究
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
知识点拨:直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法.
趁热打铁
1、如果从长度分别为2、4、6、7的四条线段中随机抽取三条线段,求抽取的三条线段能构成三角形的概率.
解:从长度分别为2、4、6、7的四条线段中随机抽取三条线段,它们为2,4,6;2,4,7;2,6,7;4,6,7,共有4种等可能的结果,
其中三条线段能构成三角形的有2种结果,
所以三条线段能构成三角形的概率为
合作探究
探究一:列表法
同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)
两个骰子的点数相同;
(2)
两个骰子点数的和是9;
(3)
至少有一个骰子的点数为2.
分析:当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
如何列表呢?
合作探究
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
合作探究
把两个骰子分别标记为第1个和第2个,列表如下:
第
一
个
第
二
个
注意有序数对要统一顺序
合作探究
解:由列表得,同时掷两枚骰子,可能出现的结果有36个,它们出现的可能性相等.
满足两枚骰子的点数相同(记为事件A)的结果有6个,则
P(A)=
;
(2)
满足两枚骰子的点数之和是9(记为事件B)的结果有4个,则P(B)=
;
(3)
满足至少有一枚骰子的点数为2(记为事件C)的结果有11个,则P(C)=
.
思考2:“同时掷两枚质地均匀的骰子”与“把一枚质地均匀的骰子掷两次”,得到的结果有变化吗?为什么?
没变化!
趁热打铁
1、一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
趁热打铁
结果
第一次
第二次
解:利用表格列出所有等可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
由上表可以看出,摸两次球可能出现的结果有9种,其中两次摸出的都是红球的结果有4种,所以:
趁热打铁
变式训练:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
合作探究
(1)用列表法求概率适用于事件中涉及两个因素,并且可能出现的
结果数目较多;
(2)在运用列表法求概率时,应注意各种结果出现的可能性相等,
要注意列表的顺序,并不重不漏地列出所有可能的结果.
第一步:列表格;
第二步:在所有可能情况n中,再找到满足条件的事件的个数m;
第三步:代入概率公式
计算事件的概率.
1.列表法求概率应注意的问题:
归纳总结:
2.列表法求概率的基本步骤:
综合演练
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是(
)
2.某次考试中,每道单项选择题有4个选项,某同学有两道单项选择题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是(
)
B
D
A.
B.
C.
D.
A.
B.
C.
D.
综合演练
3.某校组织九年级学生参加中考体育测试,共租3辆客车,分别编号为1、2、3,李军和赵娟两人可任选一辆车乘坐,则两人同坐2号车的概率为( )
A
.
B.
C.
D.
A
4.如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是(
)
A.
B.
C.
D.
B
综合演练
5.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)
摸出两张牌的数字之和为4的概率为多少?
(2)
摸出为两张牌的数字相等的概率为多少?
综合演练
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:下表列出了所有可能出现的结果,共9种.
能力提升
6、在6张卡片上分别写有1-6的整数,随机地抽取一张后不放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
1
2
3
4
5
6
1
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
第
一
张
第
二
张
能力提升
解:由列表得,两次抽取卡片后,可能出现的结果有30个,它们出现的可能性相等.
P(A)
=
=
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有8个,则
课堂总结
说一说:
1、本节课我们学习了几种列举法?分别是什么?
2、它们的适用对象满足什么条件?分别有哪些步骤?
本节课你有哪些收获?
作业布置
习题25.2
P139页:1、2、3
https://www.21cnjy.com/help/help_extract.php
同课章节目录
