人教版(五四学制)七年级上册数学 —13.3 实数 课件 (共32张PPT)
文档属性
| 名称 | 人教版(五四学制)七年级上册数学 —13.3 实数 课件 (共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 420.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 09:19:11 | ||
图片预览










文档简介
(共32张PPT)
实数
5.3的算术平方根记作
。
4.算术平方根等于本身的数是1;
它们是正确的吗?
1.-4是16的平方根;
2.16的平方根是4与-4;
3.平方根等于本身的数1,0;
观察下图,每个小正方形的边长均是1,我们可以得到小正方形的面积1,
(1)图中阴影正方形的面积是多少?
它的边长是多少?
(2)估计
的值在哪两个整数之间。
探究活动
是不是有理数?
议一议
问:
是不是整数?
是不是分数?
a
a
用这种方法可以得到一系列越来越接近
的近似值。
=1.414
213
562
373
095
048
801
688
724
209
6……
我们把这种无限不循环小数叫做无理数。
无理数的三种形式:
2)
π,
-π…
3)
0.101001000…
(两个“1”
之间依次多一个0),
-7.2121121112…
(两个“2”
之间依次多一个1)
有理数
整数
分数
正整数
1,2…
零
0
负整数
-1,-2…
负分数
,
…
正分数
,
…
知识回顾
有理数还有分类方法吗?
有理数的分类:
正有理数
零
负有理数
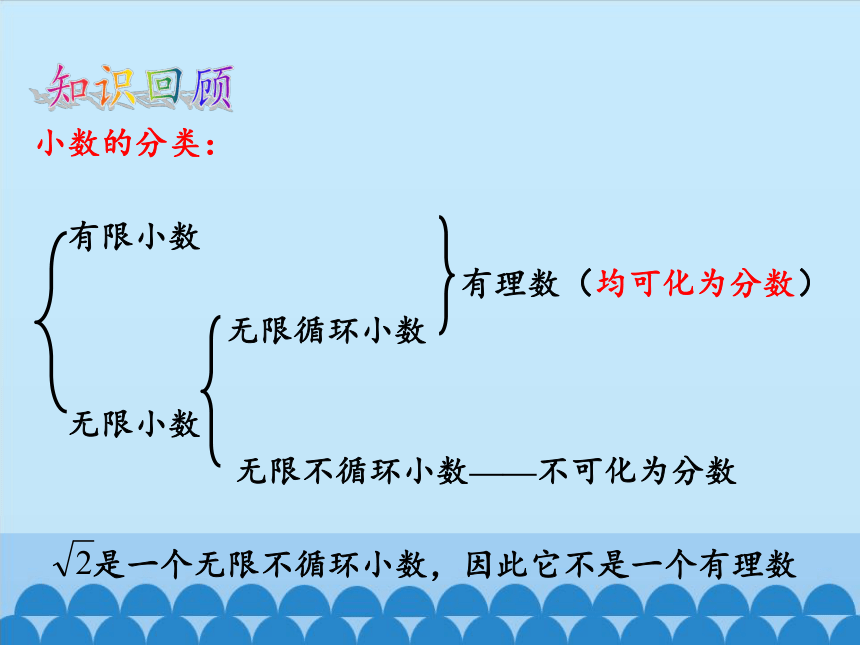
知识回顾
小数的分类:
有限小数
有理数(均可化为分数)
无限循环小数
无限小数
无限不循环小数——不可化为分数
是一个无限不循环小数,因此它不是一个有理数
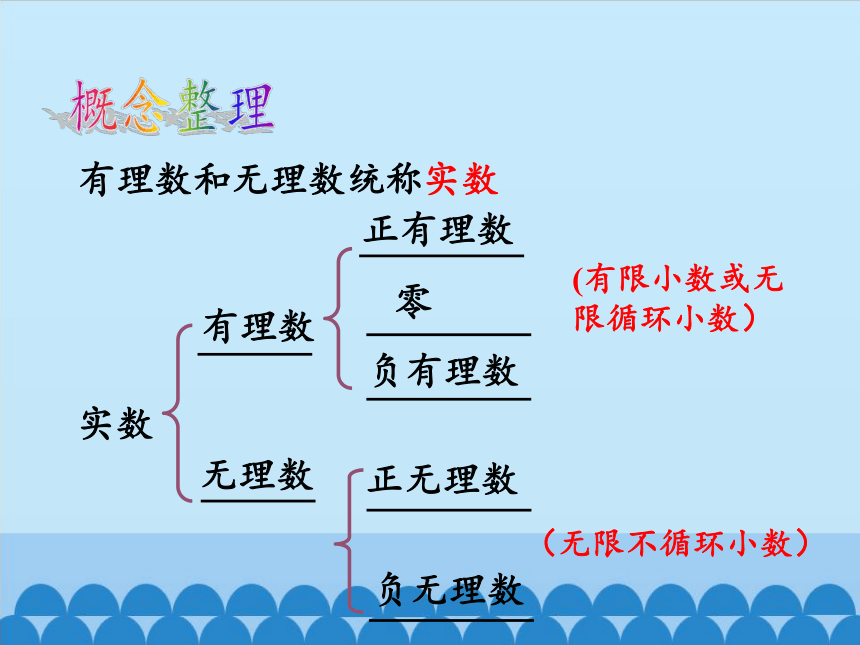
知识回顾
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有理数和无理数统称实数
(无限不循环小数)
(有限小数或无限循环小数)
概念整理
属于有理数的:
;
属于无理数的:
;
属于实数的有:
;
练一练
无理数、实数的概念,实数的分类;
小结
实数
正实数
零
负实数
正有理数
正无理数
负有理数
负无理数
分类一:
实数
有理数
无理数
整数
分数
正无理数
负无理数
分类二:
正有理数
负有理数
或
零
实数轴
单位正方形(边长为1的正方形)
按照学过的知识,你能否想象出
在数轴上的位置吗?
你能想办法在数轴上找到
表示的点吗?
相关知识:
正方形的面积=边长之积=对角线之积的一半
0
1
2
3
-1
1
2
0
1
2
-1
-2
A
一个实数a
如果将所有的有理数都标到数轴上,那么数轴将被填满吗?
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示。
即:实数与数轴上的点一一对应
归纳整理
让你的思维动起来
想一想:
是有理数还是无理数?
判断:
带有根号的数一定是无理数(
)
无理数一定含有根号(
)
无限小数一定是无理数(
)
无理数的绝对值一定是无理数
(
)
两无理数的和一定是无理数(
)
两个无理数的积一定是无理数
(
)
有理数与数轴上的点一一对应(
)
×
×
×
×
×
√
×
把数从有理数扩充到实数后,有理数的相反数、倒数和绝对值的概念同样适用于实数。
例如:
和
互为相反数。
∴绝对值等于
的数是
实数和有理数一样,也可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算,而且有理数的运算法则和运算律对于实数仍然适用。
例1
近似计算
两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点所表示的数。在实数范围内也有:
正数大于0,负数小于0,正数大于负数。
两个正数,绝对值大的数较大。
两个负数,绝对值小的数反而较大。
例2
把下列实数表示在数轴上,并比较它们的
大小(用“<”号连接)
-2
-1
0
1
2
3
4
5
·
·
·
·
·
·
-2
-1
0
1
2
3
4
5
你能在数轴上表示出
吗?
试一试:
a是一个实数,它的相反数为
;
绝对值为
。如果a≠0,那么它的
倒数为
。
想一想
填空:
5.一个数的绝对值是π,这个数是
;
(1)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(2)相反数、绝对值、数的大小比较法则同样适用于实数。
小结
比较下列各组里两个数的大小。
随堂练习
布置作业
1.草稿纸作业
2.课堂作业
谢
谢
实数
5.3的算术平方根记作
。
4.算术平方根等于本身的数是1;
它们是正确的吗?
1.-4是16的平方根;
2.16的平方根是4与-4;
3.平方根等于本身的数1,0;
观察下图,每个小正方形的边长均是1,我们可以得到小正方形的面积1,
(1)图中阴影正方形的面积是多少?
它的边长是多少?
(2)估计
的值在哪两个整数之间。
探究活动
是不是有理数?
议一议
问:
是不是整数?
是不是分数?
a
a
用这种方法可以得到一系列越来越接近
的近似值。
=1.414
213
562
373
095
048
801
688
724
209
6……
我们把这种无限不循环小数叫做无理数。
无理数的三种形式:
2)
π,
-π…
3)
0.101001000…
(两个“1”
之间依次多一个0),
-7.2121121112…
(两个“2”
之间依次多一个1)
有理数
整数
分数
正整数
1,2…
零
0
负整数
-1,-2…
负分数
,
…
正分数
,
…
知识回顾
有理数还有分类方法吗?
有理数的分类:
正有理数
零
负有理数
知识回顾
小数的分类:
有限小数
有理数(均可化为分数)
无限循环小数
无限小数
无限不循环小数——不可化为分数
是一个无限不循环小数,因此它不是一个有理数
知识回顾
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有理数和无理数统称实数
(无限不循环小数)
(有限小数或无限循环小数)
概念整理
属于有理数的:
;
属于无理数的:
;
属于实数的有:
;
练一练
无理数、实数的概念,实数的分类;
小结
实数
正实数
零
负实数
正有理数
正无理数
负有理数
负无理数
分类一:
实数
有理数
无理数
整数
分数
正无理数
负无理数
分类二:
正有理数
负有理数
或
零
实数轴
单位正方形(边长为1的正方形)
按照学过的知识,你能否想象出
在数轴上的位置吗?
你能想办法在数轴上找到
表示的点吗?
相关知识:
正方形的面积=边长之积=对角线之积的一半
0
1
2
3
-1
1
2
0
1
2
-1
-2
A
一个实数a
如果将所有的有理数都标到数轴上,那么数轴将被填满吗?
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示。
即:实数与数轴上的点一一对应
归纳整理
让你的思维动起来
想一想:
是有理数还是无理数?
判断:
带有根号的数一定是无理数(
)
无理数一定含有根号(
)
无限小数一定是无理数(
)
无理数的绝对值一定是无理数
(
)
两无理数的和一定是无理数(
)
两个无理数的积一定是无理数
(
)
有理数与数轴上的点一一对应(
)
×
×
×
×
×
√
×
把数从有理数扩充到实数后,有理数的相反数、倒数和绝对值的概念同样适用于实数。
例如:
和
互为相反数。
∴绝对值等于
的数是
实数和有理数一样,也可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算,而且有理数的运算法则和运算律对于实数仍然适用。
例1
近似计算
两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点所表示的数。在实数范围内也有:
正数大于0,负数小于0,正数大于负数。
两个正数,绝对值大的数较大。
两个负数,绝对值小的数反而较大。
例2
把下列实数表示在数轴上,并比较它们的
大小(用“<”号连接)
-2
-1
0
1
2
3
4
5
·
·
·
·
·
·
-2
-1
0
1
2
3
4
5
你能在数轴上表示出
吗?
试一试:
a是一个实数,它的相反数为
;
绝对值为
。如果a≠0,那么它的
倒数为
。
想一想
填空:
5.一个数的绝对值是π,这个数是
;
(1)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(2)相反数、绝对值、数的大小比较法则同样适用于实数。
小结
比较下列各组里两个数的大小。
随堂练习
布置作业
1.草稿纸作业
2.课堂作业
谢
谢
