人教版(五四学制)七年级上册数学 —12.2 平行线及其判定 课件 (共24张PPT)
文档属性
| 名称 | 人教版(五四学制)七年级上册数学 —12.2 平行线及其判定 课件 (共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 972.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 09:22:41 | ||
图片预览








文档简介
(共24张PPT)
平行线及其判定
1.能根据“同位角相等,两直线平行”证明“同旁内角互补,两直线平行”“内错角相等,两直线平行”,并能简单地应用这些结论。
2.初步了解证明的基本步骤和书写格式。
3.体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力。
请找出图中的平行线!
它们为什么平行?
公理
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由.
a
b
c
1
3
2
已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b
证明:∵
∠1与∠2互补
(已知),
∴∠1+∠2=180°(互补的定义).
∴∠1=
180°-∠2(等式的性质).
又∵∠3+∠2=180°
(平角的定义),
∴∠3=
180°-∠2(等式的性质).
∴∠1=∠3(等量代换).
∴
a∥b(同位角相等,两直线平行).
已给的公理,定义和定理以后都可以作为依据,用来证明新的命题.
说说你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项.
定理
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行
∵
∠1+
∠2=180°
∴
a∥b
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
1
a
b
c
2
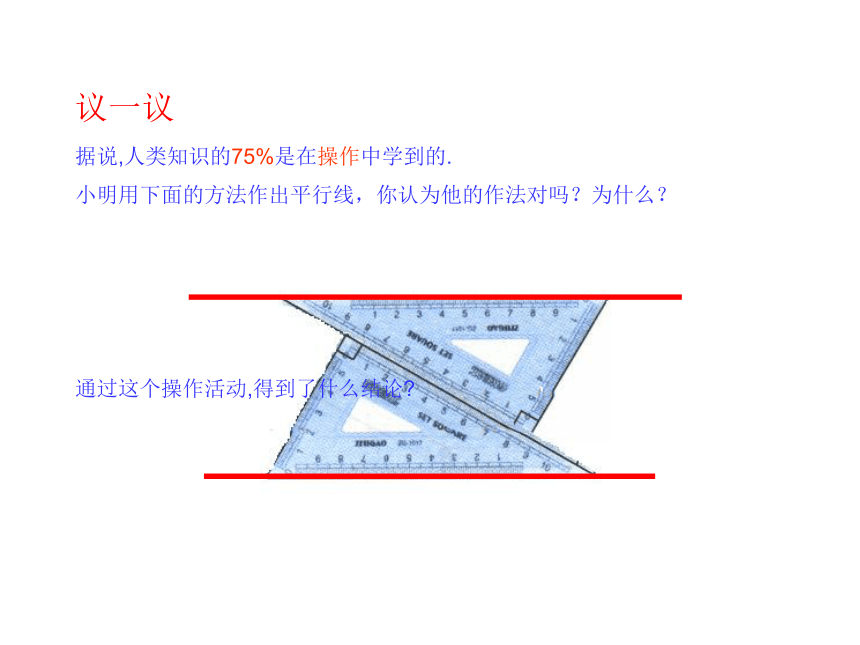
据说,人类知识的75%是在操作中学到的.
小明用下面的方法作出平行线,你认为他的作法对吗?为什么?
通过这个操作活动,得到了什么结论?
议一议
定理
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
这个定理可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗?
a
b
c
1
3
2
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b.
证明:∵∠1=∠2
(已知),
∠1+∠3=180°(平角的定义).
∴∠2+∠3
=
180°(等量代换).
∴∠2与∠3互补(互补的意义).
∴
a∥b(同旁内角互补,两直线平行).
把你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项内化为一种方法.
借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论?
C
E
B
A
D
2
1
3
如图:直线AB、CD都和AE相交,且
∠1+∠A=180°.
求证:AB//CD
【跟踪训练】
证明:∵∠1+∠3=180°(1平角=180°),
∠2+∠3=180°(
),
∴∠1=∠2(等量代换).
∵∠1+∠A=180°(
),
∴∠2+∠A=180°(等量代换).
∴AB‖CD
(
)
你还有其他证明方法吗?
已知
同旁内角互补,两直线平行
1平角=180°
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵
∠1=∠2,
∴
a∥b.
判定定理1:
内错角相等,两直线平行.
∵
∠1=∠2,
∴
a∥b.
判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=180°,
∴
a∥b.
平行线的判定方法
蜜蜂的本领
达尔文曾经说过:“蜜蜂巢房的精巧构造十分符合需要,如果一个人看到巢房而不倍加赞扬,那他一定是个糊涂虫.”这些小小的动物,它们用蜂蜡一昼夜可以造出几千间巢房,而且每间的体积几乎都是0.25
cm3,壁厚都精确地保持在0.073±0.002
mm范围内.如果你仔细进行观察就会发现,每个巢房从正面看去都是正六边形(每个角都是120°),而它的尖顶形成的底部则都是由三个完全相同的菱形拼接而成的.十八世纪初,法国学者马拉尔其经过测量发现,所有的底部菱形的钝角都等于109°28′,而其锐角都等于70°32′。法国物理学家列奥缪拉由这个有趣的发现得到一个启示:蜂房的这一特殊形状,可能是为了保证得到同样大的容积而所用材料最省.多么令人惊奇,小小的蜜蜂在人类有史以前就已经解决了的问题,十八世纪的数学家竟要用高等数学才能解决!
读一读
β
β
数学就在我们身边!
蜂房的底部由三个全等的四边形围成,每个四边形的形状如图所示,其中∠α=109°28′,
∠β=70°32′.
试确定这三个四边形的形状,并说明你的理由.
想一想
解:平行四边形.理由如下:
∵∠A+∠D=180°
∴
AB∥CD.
同理可证:AD∥BC.
∴
ABCD为平行四边形.
即所求三个四边形为平行四边形.
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
1.对于图中标记的各角,下列条件能够推理得到a∥b的是(
)
A.∠1=∠2
B.∠2=∠4
C.∠3=∠4
D.∠1+∠4=180°
【解析】选D
∠1的对顶角与∠4是同旁内角,若∠1+
∠4=180°,可以根据同旁内角互补,两直线平行得到a∥b.
2.如图所示,∠1=75°,要使a∥b,则∠2等于(
)
A.75°
B.95°
C.105°
D.115°
【解析】选C
∠1的同位角与∠2互为补角,所以∠2=180°-75°=105°
a
b
1
2
3.如图,直线AB,CD与EF相交于G,H,下列条件:
①∠1=∠2;
②∠3=∠6;
③∠2=∠8;
④∠5+∠8=180°,
其中能判定AB∥CD的是(
)
A.①③
B.①②④
C.①③④
D.②③④
【解析】选B
∠1和∠2是同位角,因此已知∠1=∠2,可得AB∥CD;∠3和∠6是内错角,因此已知∠3=∠6,可得AB∥CD;∠2和∠8是对顶角,因此由∠2=∠8不能得到AB∥CD;由∠5+∠8=180°,可以得到∠6+∠7=180°,再根据同旁内角互补,两直线平行,可以得到AB∥CD
4.如图,请填写一个你认为恰当的条件______,使AB∥CD.
【解析】此题答案不唯一,填写的条件可以是∠CDA=
∠DAB或∠PCD=∠BAC或∠BAC+∠ACD=180°等。
答案:答案不唯一,如∠CDA=∠DAB
通过本课时的学习,需要我们掌握:
1.两条直线被第三条直线所截,会产生同位角、内错角、同旁内角.角的关系决定了两条直线是否平行,因此在做题时要掌握好“三线八角”;
2.同位角相等、内错角相等,两直线平行;同旁内角互补两直线平行.
言论的花,开得愈大;行为的果子,结得愈小。
——冰心
平行线及其判定
1.能根据“同位角相等,两直线平行”证明“同旁内角互补,两直线平行”“内错角相等,两直线平行”,并能简单地应用这些结论。
2.初步了解证明的基本步骤和书写格式。
3.体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力。
请找出图中的平行线!
它们为什么平行?
公理
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由.
a
b
c
1
3
2
已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b
证明:∵
∠1与∠2互补
(已知),
∴∠1+∠2=180°(互补的定义).
∴∠1=
180°-∠2(等式的性质).
又∵∠3+∠2=180°
(平角的定义),
∴∠3=
180°-∠2(等式的性质).
∴∠1=∠3(等量代换).
∴
a∥b(同位角相等,两直线平行).
已给的公理,定义和定理以后都可以作为依据,用来证明新的命题.
说说你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项.
定理
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行
∵
∠1+
∠2=180°
∴
a∥b
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
1
a
b
c
2
据说,人类知识的75%是在操作中学到的.
小明用下面的方法作出平行线,你认为他的作法对吗?为什么?
通过这个操作活动,得到了什么结论?
议一议
定理
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
这个定理可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗?
a
b
c
1
3
2
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b.
证明:∵∠1=∠2
(已知),
∠1+∠3=180°(平角的定义).
∴∠2+∠3
=
180°(等量代换).
∴∠2与∠3互补(互补的意义).
∴
a∥b(同旁内角互补,两直线平行).
把你所悟到的证明一个命题的方法,步骤,书写格式以及注意事项内化为一种方法.
借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论?
C
E
B
A
D
2
1
3
如图:直线AB、CD都和AE相交,且
∠1+∠A=180°.
求证:AB//CD
【跟踪训练】
证明:∵∠1+∠3=180°(1平角=180°),
∠2+∠3=180°(
),
∴∠1=∠2(等量代换).
∵∠1+∠A=180°(
),
∴∠2+∠A=180°(等量代换).
∴AB‖CD
(
)
你还有其他证明方法吗?
已知
同旁内角互补,两直线平行
1平角=180°
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵
∠1=∠2,
∴
a∥b.
判定定理1:
内错角相等,两直线平行.
∵
∠1=∠2,
∴
a∥b.
判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=180°,
∴
a∥b.
平行线的判定方法
蜜蜂的本领
达尔文曾经说过:“蜜蜂巢房的精巧构造十分符合需要,如果一个人看到巢房而不倍加赞扬,那他一定是个糊涂虫.”这些小小的动物,它们用蜂蜡一昼夜可以造出几千间巢房,而且每间的体积几乎都是0.25
cm3,壁厚都精确地保持在0.073±0.002
mm范围内.如果你仔细进行观察就会发现,每个巢房从正面看去都是正六边形(每个角都是120°),而它的尖顶形成的底部则都是由三个完全相同的菱形拼接而成的.十八世纪初,法国学者马拉尔其经过测量发现,所有的底部菱形的钝角都等于109°28′,而其锐角都等于70°32′。法国物理学家列奥缪拉由这个有趣的发现得到一个启示:蜂房的这一特殊形状,可能是为了保证得到同样大的容积而所用材料最省.多么令人惊奇,小小的蜜蜂在人类有史以前就已经解决了的问题,十八世纪的数学家竟要用高等数学才能解决!
读一读
β
β
数学就在我们身边!
蜂房的底部由三个全等的四边形围成,每个四边形的形状如图所示,其中∠α=109°28′,
∠β=70°32′.
试确定这三个四边形的形状,并说明你的理由.
想一想
解:平行四边形.理由如下:
∵∠A+∠D=180°
∴
AB∥CD.
同理可证:AD∥BC.
∴
ABCD为平行四边形.
即所求三个四边形为平行四边形.
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
1.对于图中标记的各角,下列条件能够推理得到a∥b的是(
)
A.∠1=∠2
B.∠2=∠4
C.∠3=∠4
D.∠1+∠4=180°
【解析】选D
∠1的对顶角与∠4是同旁内角,若∠1+
∠4=180°,可以根据同旁内角互补,两直线平行得到a∥b.
2.如图所示,∠1=75°,要使a∥b,则∠2等于(
)
A.75°
B.95°
C.105°
D.115°
【解析】选C
∠1的同位角与∠2互为补角,所以∠2=180°-75°=105°
a
b
1
2
3.如图,直线AB,CD与EF相交于G,H,下列条件:
①∠1=∠2;
②∠3=∠6;
③∠2=∠8;
④∠5+∠8=180°,
其中能判定AB∥CD的是(
)
A.①③
B.①②④
C.①③④
D.②③④
【解析】选B
∠1和∠2是同位角,因此已知∠1=∠2,可得AB∥CD;∠3和∠6是内错角,因此已知∠3=∠6,可得AB∥CD;∠2和∠8是对顶角,因此由∠2=∠8不能得到AB∥CD;由∠5+∠8=180°,可以得到∠6+∠7=180°,再根据同旁内角互补,两直线平行,可以得到AB∥CD
4.如图,请填写一个你认为恰当的条件______,使AB∥CD.
【解析】此题答案不唯一,填写的条件可以是∠CDA=
∠DAB或∠PCD=∠BAC或∠BAC+∠ACD=180°等。
答案:答案不唯一,如∠CDA=∠DAB
通过本课时的学习,需要我们掌握:
1.两条直线被第三条直线所截,会产生同位角、内错角、同旁内角.角的关系决定了两条直线是否平行,因此在做题时要掌握好“三线八角”;
2.同位角相等、内错角相等,两直线平行;同旁内角互补两直线平行.
言论的花,开得愈大;行为的果子,结得愈小。
——冰心
