人教版(五四学制)七年级上册数学 —11.2 解一元一次方程(一)——合并同类项与移项 课件 (共32张PPT)
文档属性
| 名称 | 人教版(五四学制)七年级上册数学 —11.2 解一元一次方程(一)——合并同类项与移项 课件 (共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 362.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 09:23:30 | ||
图片预览











文档简介
(共32张PPT)
解一元一次方程(一)——
合并同类项与移项
第1课时
合并同类项
约公元820年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.“对消”与“还原”是什么意思呢?
数学小资料
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了多少台计算机?
分析:
设前年这个学校购买了计算机x台,则去年购买计算机_____台,今年购买计算机_____台.
问题中的相等关系:
前年购买量+去年购买量+今年购买量=140台
根据题意,列得方程
x
+
2x
+4x
=
140.
2x
4x
某校三年共购买计算机140台,去年购买数
量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
还有不同的设法么?还可以列怎样的方程?
设去年购买计算机x台.
设今年购买计算机x台.
方法二:
方法三:
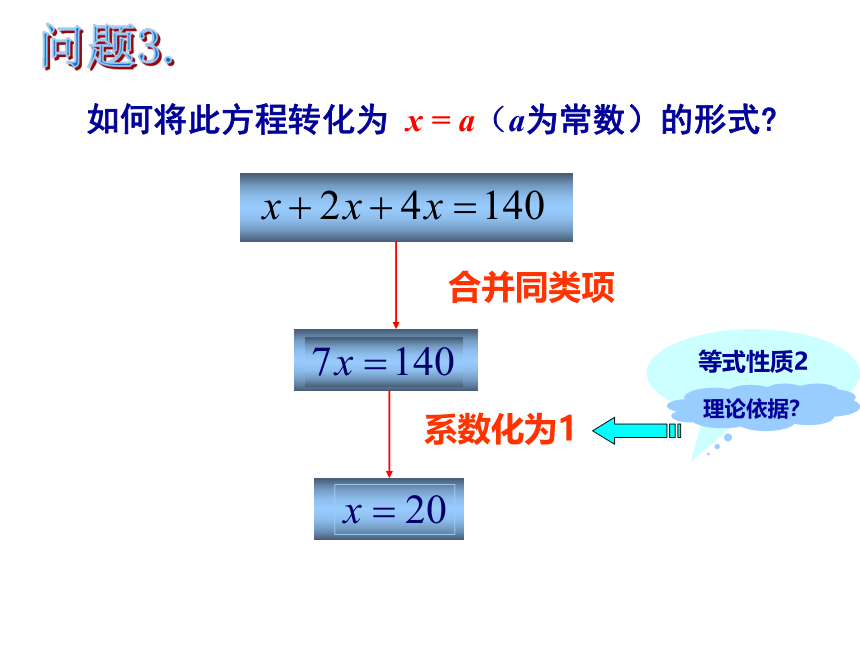
如何将此方程转化为
x
=
a(a为常数)的形式?
合并同类项
系数化为1
等式性质2
理论依据?
合并同类项,得
系数化为1,得
解方程
解:
合并同类项,得
系数化为1,得
解方程
解:
课堂练习:
教科书第88页练习第1题.
小结:
1.今天学习的解方程有哪些步骤?
2.合并同类项在解方程的过程中起到了
什么作用?
驶向胜利的彼岸
合并同类项的目的就是化简方程,
它是一种恒等变形,可以使方程变得简
单,并逐步使方程向x=a的形式转化
.
合并同类项的作用:
有一列数,按一定规律排列成
1,-3,9,-27,81,-243,···,
其中某三个相邻数的和是-1
701,
这三个数各是多少?
这列数有什么规律?
如何设未知数?
解:设这三个相邻数中第1个数为
,
则第2个数为
,第三个数为
.
根据这三个数的和是-1
701,得
合并同类项,得
系数化为1,得
所以
答:这三个数是-243,729,-2
187.
解:设这三个相邻数中的中间的一个数为
,
则第1个数为
,第三个数为
.
根据这三个数的和是-1
701,得
解得
解:设这三个相邻数中最后1个数为
,
则第2个数为
,第1个数为
.
根据这三个数的和是-1
701,得
解得
1.三个连续的奇数的和是39,求这三个数.
2.
某校开展的数学课外兴趣小组活动,每周四进行一次活动,现知本月连续的三次活动的日子之和为27,你知道是哪三天吗?本月的四次活动的日子之和是多少呢?
课堂练习
课堂小结
1.今天学习的解方程有哪些步骤?
2.谈谈用一元一次方程分析和解决实际问题
的一般过程.
作业:
1.教科书91页习题3.2练习题第1
题.
2.三个连续整数之和为36,
求:这三个整数分别是多少?
第2课时
移项
解一元一次方程(一)
复习旧知
1.等式的性质
2.口算下列方程
⑴2x=6
⑵
6x-4x=2
性质1
等式两边同时加上(或减去)同一个数(或式子),结果仍相等
性质2
等式两边同时乘以(或除以)一个不为0的数,结果仍相等
任务一
探究如何移项
元旦期间,李小花同学带一些钱去买衣服.正值商场打折,衣服打7折,鞋子打8折,如果买衣服剩30元,如果买鞋子差10元,你能计算出她带了多少钱去吗?
解
:
设她带了x元,则可列方程
0.8x
–
10
=
0.7x
+
30
0.8x
–10
=
0.7x
+
30
提问1.怎样解这个方程?它与上节课遇到的方程有何不同?
探究交流
提问2.如何才能使这个方程向x=a的形式转化?
0.8x
-10
=0.7
x
+30
0.8x
–
0.7x
=
30+10
你发现了什么?
像上面那样把等式一边的某项变号后移到另一边,叫做移项.
移项要变号,不移项不变号
提问3.以上解方程变形的依据是什么?
等式的性质1
提问4.
“移项”起了什么作用?
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式
慧眼识金
判断下列移项是否正确,看谁又快又准
(1)若x-4=8,则x=8-4
(2)若3a=2a+5,则-3a-2a=5
(3)若5s-2=4s+1,则5s-4s=1+2
×
×
√
x=8+4
3a-2a=5
√
动手做一做
请你来给下列一元一次方程移项
9-3y=5y+5
(2)
0.5x-0.7=6.5-1.3x
(3)3x+5=4x+1
(4)6x-7=4x-5
任务二
应用移项解一元一次解方程
例3
解下列方程
(1)3x
+
7
=
32
–
2x
解:移项,得
3x
+
2x
=
32
–
7
合并同类项,得
5x
=
25
系数化为1,得
x
=
5
合并同类项,得
解:移项,得
系数化为1,得
练习1
解下列方程:
(1)6x
–
7
=
4x
–
5
(2)6
–
3x
=
7x
–
14
例4
分析:
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
解;设这个班有x名学生
每人分3本,共分出3x本,加上剩余的20本,这批书共(3x+20)本.
每人分4本,需要4x本,减去缺的25本,这批书共(4x-25)本.
3x
+
20
=
4x
-
25
基础巩固
2.
对于方程–
3x
–
7=12x+6,下列移项正确的是(
)
A
A.
–
3x
–
12x=6+7
B.
–
3x+12x=
–
7+6
C.
–
3x
–
12x=7-6
D.12x
–
3x=6+7
3.
对方程
7x
=
6
+
4x
进行移项,得___________,合并同类项,得_________,系数化为1,得________.
7x
-
4x
=
6
3x
=
6
x
=
2
课堂小结
这节课你们有哪些收获?我们一起来分享一下吧!
1.回顾等式的性质及应用
2.用移项的方法来解一元一次方程
思路:移项→合并同类项→系数化为1
3.移项应注意:移项要变号,不移项不变号
课后作业
1.习题3.2
,第3题作业本;
2.完成创优练习册本课时的习题.
解一元一次方程(一)——
合并同类项与移项
第1课时
合并同类项
约公元820年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.“对消”与“还原”是什么意思呢?
数学小资料
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了多少台计算机?
分析:
设前年这个学校购买了计算机x台,则去年购买计算机_____台,今年购买计算机_____台.
问题中的相等关系:
前年购买量+去年购买量+今年购买量=140台
根据题意,列得方程
x
+
2x
+4x
=
140.
2x
4x
某校三年共购买计算机140台,去年购买数
量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
还有不同的设法么?还可以列怎样的方程?
设去年购买计算机x台.
设今年购买计算机x台.
方法二:
方法三:
如何将此方程转化为
x
=
a(a为常数)的形式?
合并同类项
系数化为1
等式性质2
理论依据?
合并同类项,得
系数化为1,得
解方程
解:
合并同类项,得
系数化为1,得
解方程
解:
课堂练习:
教科书第88页练习第1题.
小结:
1.今天学习的解方程有哪些步骤?
2.合并同类项在解方程的过程中起到了
什么作用?
驶向胜利的彼岸
合并同类项的目的就是化简方程,
它是一种恒等变形,可以使方程变得简
单,并逐步使方程向x=a的形式转化
.
合并同类项的作用:
有一列数,按一定规律排列成
1,-3,9,-27,81,-243,···,
其中某三个相邻数的和是-1
701,
这三个数各是多少?
这列数有什么规律?
如何设未知数?
解:设这三个相邻数中第1个数为
,
则第2个数为
,第三个数为
.
根据这三个数的和是-1
701,得
合并同类项,得
系数化为1,得
所以
答:这三个数是-243,729,-2
187.
解:设这三个相邻数中的中间的一个数为
,
则第1个数为
,第三个数为
.
根据这三个数的和是-1
701,得
解得
解:设这三个相邻数中最后1个数为
,
则第2个数为
,第1个数为
.
根据这三个数的和是-1
701,得
解得
1.三个连续的奇数的和是39,求这三个数.
2.
某校开展的数学课外兴趣小组活动,每周四进行一次活动,现知本月连续的三次活动的日子之和为27,你知道是哪三天吗?本月的四次活动的日子之和是多少呢?
课堂练习
课堂小结
1.今天学习的解方程有哪些步骤?
2.谈谈用一元一次方程分析和解决实际问题
的一般过程.
作业:
1.教科书91页习题3.2练习题第1
题.
2.三个连续整数之和为36,
求:这三个整数分别是多少?
第2课时
移项
解一元一次方程(一)
复习旧知
1.等式的性质
2.口算下列方程
⑴2x=6
⑵
6x-4x=2
性质1
等式两边同时加上(或减去)同一个数(或式子),结果仍相等
性质2
等式两边同时乘以(或除以)一个不为0的数,结果仍相等
任务一
探究如何移项
元旦期间,李小花同学带一些钱去买衣服.正值商场打折,衣服打7折,鞋子打8折,如果买衣服剩30元,如果买鞋子差10元,你能计算出她带了多少钱去吗?
解
:
设她带了x元,则可列方程
0.8x
–
10
=
0.7x
+
30
0.8x
–10
=
0.7x
+
30
提问1.怎样解这个方程?它与上节课遇到的方程有何不同?
探究交流
提问2.如何才能使这个方程向x=a的形式转化?
0.8x
-10
=0.7
x
+30
0.8x
–
0.7x
=
30+10
你发现了什么?
像上面那样把等式一边的某项变号后移到另一边,叫做移项.
移项要变号,不移项不变号
提问3.以上解方程变形的依据是什么?
等式的性质1
提问4.
“移项”起了什么作用?
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式
慧眼识金
判断下列移项是否正确,看谁又快又准
(1)若x-4=8,则x=8-4
(2)若3a=2a+5,则-3a-2a=5
(3)若5s-2=4s+1,则5s-4s=1+2
×
×
√
x=8+4
3a-2a=5
√
动手做一做
请你来给下列一元一次方程移项
9-3y=5y+5
(2)
0.5x-0.7=6.5-1.3x
(3)3x+5=4x+1
(4)6x-7=4x-5
任务二
应用移项解一元一次解方程
例3
解下列方程
(1)3x
+
7
=
32
–
2x
解:移项,得
3x
+
2x
=
32
–
7
合并同类项,得
5x
=
25
系数化为1,得
x
=
5
合并同类项,得
解:移项,得
系数化为1,得
练习1
解下列方程:
(1)6x
–
7
=
4x
–
5
(2)6
–
3x
=
7x
–
14
例4
分析:
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
解;设这个班有x名学生
每人分3本,共分出3x本,加上剩余的20本,这批书共(3x+20)本.
每人分4本,需要4x本,减去缺的25本,这批书共(4x-25)本.
3x
+
20
=
4x
-
25
基础巩固
2.
对于方程–
3x
–
7=12x+6,下列移项正确的是(
)
A
A.
–
3x
–
12x=6+7
B.
–
3x+12x=
–
7+6
C.
–
3x
–
12x=7-6
D.12x
–
3x=6+7
3.
对方程
7x
=
6
+
4x
进行移项,得___________,合并同类项,得_________,系数化为1,得________.
7x
-
4x
=
6
3x
=
6
x
=
2
课堂小结
这节课你们有哪些收获?我们一起来分享一下吧!
1.回顾等式的性质及应用
2.用移项的方法来解一元一次方程
思路:移项→合并同类项→系数化为1
3.移项应注意:移项要变号,不移项不变号
课后作业
1.习题3.2
,第3题作业本;
2.完成创优练习册本课时的习题.
