必修二_2.3_线、面垂直的判定及其性质_教案
文档属性
| 名称 | 必修二_2.3_线、面垂直的判定及其性质_教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 138.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-16 00:00:00 | ||
图片预览

文档简介
必修2 2.3 线、面垂直的判定及其性质 教案
2.3.1 直线与平面垂直的判定
一、知识梳理
1、线与面垂直的定义
如果一条直线与一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线与这个平面垂直。
问:如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?
2、线与面垂直的判定
判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
(线线垂直线面垂直)(线线垂直线面垂直线线垂直)
3、射影定理
一条直线PA和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足。在斜线上取一点(除斜足外)向平面引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的斜影。斜线与斜影所构成的锐角叫做这条直线和这个平面所成的角。因此线与面所成的角的范围是 。
如果这个平面内有一条直线与这个平面的斜线的斜影垂直,那么这条直线就与这条斜线垂直。(正方体中经常用)
4、过一点有 条直线和一个平面垂直。
过一点有 个平面和一条直线垂直。
二、例题
如右图,已知Rt△ABC所在平面外一点S,且SA=SB=SC,点D为斜边AC的中点。
求证:SD⊥平面ABC;
若AB=BC,求证:BD⊥平面SAC。
三、练习
1、如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A、B的一点,过A作AE⊥PC,再过E作EF⊥PB。求证:PB⊥AF。
2、下列命题中正确的个数是 ( )
①如果直线与平面内的无数条直线垂直,则⊥
②如果直线与平面内一条直线垂直,则 //
③如果直线不垂直于平面,则平面内没有与直线垂直的直线
④如果直线不垂直于平面,则平面内也可以有无数条直线与直线垂直
A、0 B、1 C、2 D、3
3、空间四边形的四条边相等,那么它的对角线 ( )
A、相交且垂直 B、不相交也不垂直 C、相交不垂直 D、不相交但垂直
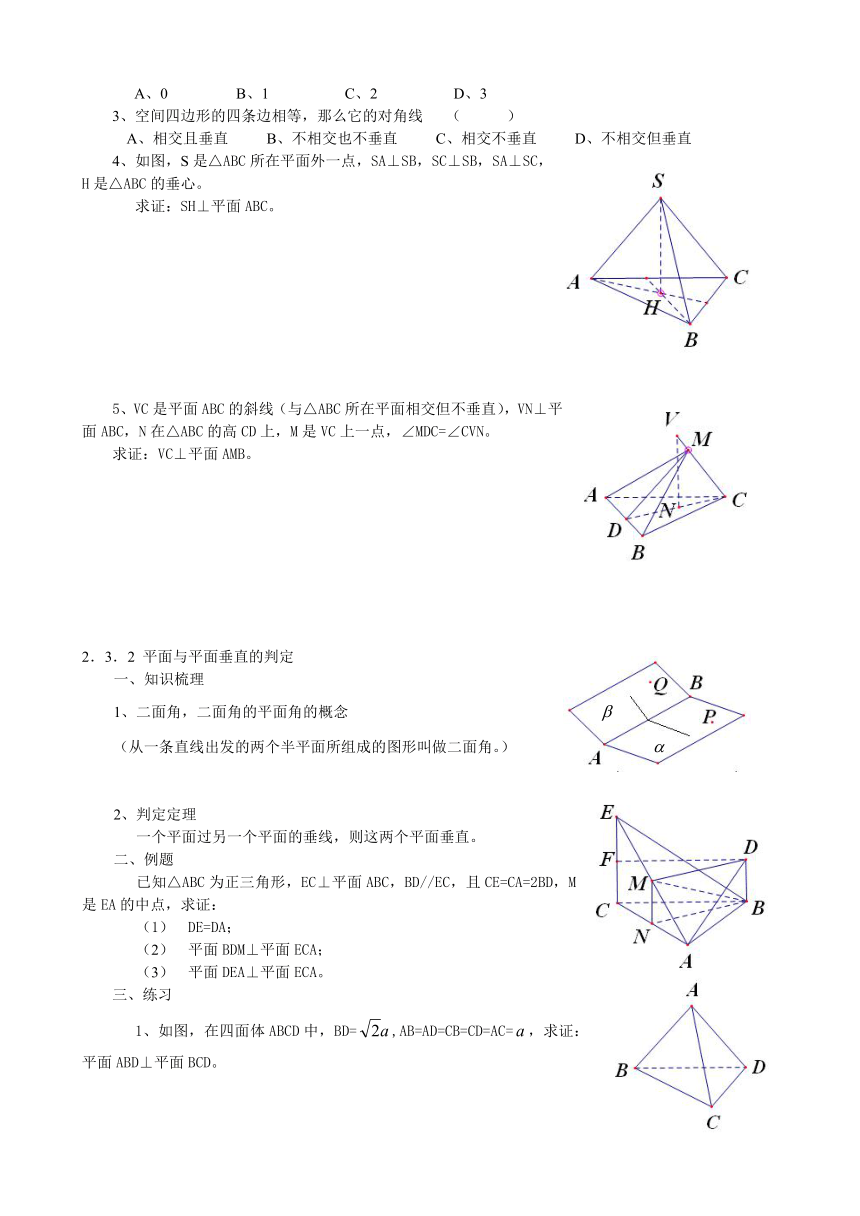
4、如图,S是△ABC所在平面外一点,SA⊥SB,SC⊥SB,SA⊥SC,H是△ABC的垂心。
求证:SH⊥平面ABC。
5、VC是平面ABC的斜线(与△ABC所在平面相交但不垂直),VN⊥平面ABC,N在△ABC的高CD上,M是VC上一点,∠MDC=∠CVN。
求证:VC⊥平面AMB。
2.3.2 平面与平面垂直的判定
一、知识梳理
1、二面角,二面角的平面角的概念
(从一条直线出发的两个半平面所组成的图形叫做二面角。)
2、判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
二、例题
已知△ABC为正三角形,EC⊥平面ABC,BD//EC,且CE=CA=2BD,M是EA的中点,求证:
DE=DA;
平面BDM⊥平面ECA;
平面DEA⊥平面ECA。
三、练习
1、如图,在四面体ABCD中,BD=,AB=AD=CB=CD=AC=,求证:平面ABD⊥平面BCD。
2、如图,ABC—A1B1C1是直棱柱,△A1B1C1是正三角形,E是C C1的中点。
求证:平面A B1E⊥平面A A1B1B。
3、如图,在正方体ABCD—A’B’C’D’中,求二面角B—A’B’—B’的正切值。
4、设有直线m,n和平面、,则下列命题中,正确的是 ( )
A、若m // n,m,n,则//
B、若m⊥,m⊥n,n,则//
C、若m // n,n⊥,m,则⊥
D、若m // n,m⊥,n⊥,则⊥
5、如图,P是二面角—AB—的棱上AB一点,分别在
、上引射线PM、PN,如果∠BPM=∠BPN=45°,∠MPN
=60°,则二面角—AB—的大小是 。
6、如图,已知三棱锥A—BCD的三个侧面与底面全等且BC=BD=,CD=2,则二面角A—CD—B的大小是 。
2.3.3 直线与平面垂直的性质
一、知识梳理
1、过一点和已知平面垂直的直线 。
2、过一点和一条直线垂直的平面 。
3、垂直于同一平面的两条直线 。
4、垂直于同一直线的两个平面 。
二、例题
在△ABC中,∠ABC=90°,SA⊥平面ABC,点A在SB、SC上的射影分别为点E、F,求证:EF⊥SC。
三、练习
1、如图,正方体ABCD—A’B’C’D’中,EF是异面直线AC及A’D的公垂线。
求证:EF//BD’.
2、如图,正方体ABCD—A’B’C’D’中,E、F、G分别是A’B’、 B’C’和B B’的中点。
求证: (1)面AC C’ A’ ⊥面BD D’ B’;
面ACFE⊥面BD D’ B’;
面ACG⊥面BD D’ B’。
2.3.4 平面与平面垂直的性质
一、知识梳理
性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
二、例题
如图,已知平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足。
(1)求证:PA⊥面ABC;
(2)当E为△PBC的垂心时,求证:△ABC是直角三角形。
三、练习
1、如图,ABCD—A’B’C’D’是正方体,判断直线A’C与平面B C’D的位置关系,并说明理由。
2、空间四边形SABC中,SO⊥面ABC,O为△ABC的垂心。求证:平面SOC⊥面SAB。
2.3.1 直线与平面垂直的判定
一、知识梳理
1、线与面垂直的定义
如果一条直线与一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线与这个平面垂直。
问:如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?
2、线与面垂直的判定
判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
(线线垂直线面垂直)(线线垂直线面垂直线线垂直)
3、射影定理
一条直线PA和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足。在斜线上取一点(除斜足外)向平面引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的斜影。斜线与斜影所构成的锐角叫做这条直线和这个平面所成的角。因此线与面所成的角的范围是 。
如果这个平面内有一条直线与这个平面的斜线的斜影垂直,那么这条直线就与这条斜线垂直。(正方体中经常用)
4、过一点有 条直线和一个平面垂直。
过一点有 个平面和一条直线垂直。
二、例题
如右图,已知Rt△ABC所在平面外一点S,且SA=SB=SC,点D为斜边AC的中点。
求证:SD⊥平面ABC;
若AB=BC,求证:BD⊥平面SAC。
三、练习
1、如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A、B的一点,过A作AE⊥PC,再过E作EF⊥PB。求证:PB⊥AF。
2、下列命题中正确的个数是 ( )
①如果直线与平面内的无数条直线垂直,则⊥
②如果直线与平面内一条直线垂直,则 //
③如果直线不垂直于平面,则平面内没有与直线垂直的直线
④如果直线不垂直于平面,则平面内也可以有无数条直线与直线垂直
A、0 B、1 C、2 D、3
3、空间四边形的四条边相等,那么它的对角线 ( )
A、相交且垂直 B、不相交也不垂直 C、相交不垂直 D、不相交但垂直
4、如图,S是△ABC所在平面外一点,SA⊥SB,SC⊥SB,SA⊥SC,H是△ABC的垂心。
求证:SH⊥平面ABC。
5、VC是平面ABC的斜线(与△ABC所在平面相交但不垂直),VN⊥平面ABC,N在△ABC的高CD上,M是VC上一点,∠MDC=∠CVN。
求证:VC⊥平面AMB。
2.3.2 平面与平面垂直的判定
一、知识梳理
1、二面角,二面角的平面角的概念
(从一条直线出发的两个半平面所组成的图形叫做二面角。)
2、判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
二、例题
已知△ABC为正三角形,EC⊥平面ABC,BD//EC,且CE=CA=2BD,M是EA的中点,求证:
DE=DA;
平面BDM⊥平面ECA;
平面DEA⊥平面ECA。
三、练习
1、如图,在四面体ABCD中,BD=,AB=AD=CB=CD=AC=,求证:平面ABD⊥平面BCD。
2、如图,ABC—A1B1C1是直棱柱,△A1B1C1是正三角形,E是C C1的中点。
求证:平面A B1E⊥平面A A1B1B。
3、如图,在正方体ABCD—A’B’C’D’中,求二面角B—A’B’—B’的正切值。
4、设有直线m,n和平面、,则下列命题中,正确的是 ( )
A、若m // n,m,n,则//
B、若m⊥,m⊥n,n,则//
C、若m // n,n⊥,m,则⊥
D、若m // n,m⊥,n⊥,则⊥
5、如图,P是二面角—AB—的棱上AB一点,分别在
、上引射线PM、PN,如果∠BPM=∠BPN=45°,∠MPN
=60°,则二面角—AB—的大小是 。
6、如图,已知三棱锥A—BCD的三个侧面与底面全等且BC=BD=,CD=2,则二面角A—CD—B的大小是 。
2.3.3 直线与平面垂直的性质
一、知识梳理
1、过一点和已知平面垂直的直线 。
2、过一点和一条直线垂直的平面 。
3、垂直于同一平面的两条直线 。
4、垂直于同一直线的两个平面 。
二、例题
在△ABC中,∠ABC=90°,SA⊥平面ABC,点A在SB、SC上的射影分别为点E、F,求证:EF⊥SC。
三、练习
1、如图,正方体ABCD—A’B’C’D’中,EF是异面直线AC及A’D的公垂线。
求证:EF//BD’.
2、如图,正方体ABCD—A’B’C’D’中,E、F、G分别是A’B’、 B’C’和B B’的中点。
求证: (1)面AC C’ A’ ⊥面BD D’ B’;
面ACFE⊥面BD D’ B’;
面ACG⊥面BD D’ B’。
2.3.4 平面与平面垂直的性质
一、知识梳理
性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
二、例题
如图,已知平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足。
(1)求证:PA⊥面ABC;
(2)当E为△PBC的垂心时,求证:△ABC是直角三角形。
三、练习
1、如图,ABCD—A’B’C’D’是正方体,判断直线A’C与平面B C’D的位置关系,并说明理由。
2、空间四边形SABC中,SO⊥面ABC,O为△ABC的垂心。求证:平面SOC⊥面SAB。
