分类加法计数原理与分步乘法计数原理(3课时)
文档属性
| 名称 | 分类加法计数原理与分步乘法计数原理(3课时) |  | |
| 格式 | zip | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-16 16:15:43 | ||
图片预览










文档简介
(共66张PPT)
分类加法计数原理
与
分步乘法计数原理
(一)
〖教学目的〗
1、知识与技能:分类与分步原理及其应用。
2、过程与方法:通过实例探究,找到两个记数原理,理解两个原理的内容。
3、情感态度与价值观:要求学生在现实生活中面对复杂的事物和现象,能够作出正确的分析和判断,进而拿出完善的处理方案,提高实际应变能力,从而认识数学知识与现实生活的内在联系
〖教学重点〗
归纳地得出分类加法计数原理和分步乘法计数原理,能应用它们解决简单的实际问题.
〖教学难点〗
正确理解“完成一件事情”的含义;根据实际问题的特征,正确地区分“分类”或“分步”.
问题1:用一个大写的的英文字母或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
26+10=36(种)
问题2:从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船.一天中,火车有4 班,汽车有2班,轮船有3班.那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
分析: 从甲地到乙地有3类方法:
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有
4 + 2 + 3 = 9
种方法。
基础知识
一、分类加法计数原理
完成一件事,有n类办法. 在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,则完成这件事共有
种不同的方法。
N= m1+m2+… +mn
(加法原理)
弄清要完成哪件事情
类与类之间互不相容,各类中的方法也互不相同
例1:在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自已感兴趣的强项专业,具体情况如下: A大学 B大学 生物学 数学 化学 会计学 医学 信息技术学 物理学 法学 工程学 那么,这名同学可能的专业选择共有多少种
分类加法计数原理:5+4=9(种)
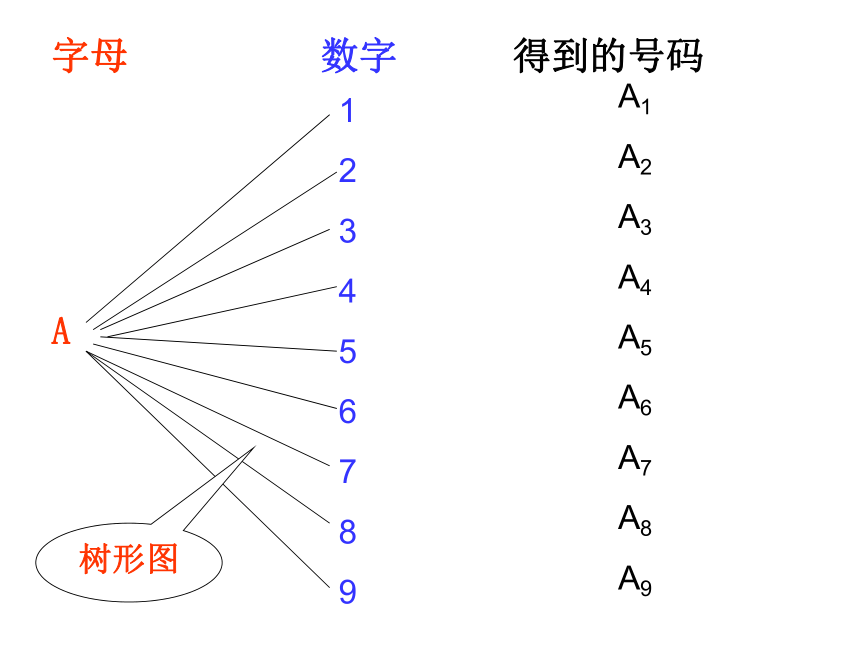
问题3:用前6个大写英文字母和1-9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少个不同的号码?
字母 数字 得到的号码
A
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
树形图
由于前6个英文字母中的任意一个都能与9个数字中的任何一个组成一个号码,而且它们各个不同,因此共有
6×9=54
个不同的号码.
问题3:用前6个大写英文字母和1-9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少个不同的号码?
汽车有2班,那么两天中,从甲地到乙地共有多少种不同的走法?
所有走法:
如何计算所有不同走法的种数?
∵乘火车有3种走法,乘汽车有2种走法,
∴乘一次火车再换乘一次汽车从甲地到乙地,
共有3×2=6种不同的走法。
问题4:从甲地到乙地,要从甲地先乘火车到丙地,再于
次日从丙地乘汽车到乙地。
已知从一天中,火车有3班,
基础知识
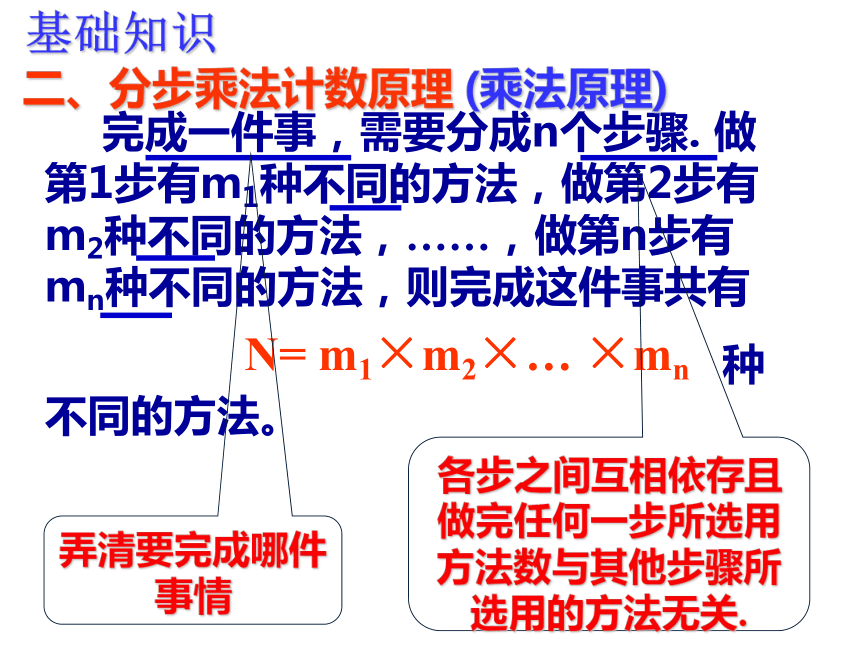
二、分步乘法计数原理
完成一件事,需要分成n个步骤. 做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,则完成这件事共有
种不同的方法。
N= m1×m2×… ×mn
(乘法原理)
弄清要完成哪件事情
各步之间互相依存且做完任何一步所选用方法数与其他步骤所选用的方法无关.
分步加法计数原理和分类乘法计数原理的共同点:
计算做一件事情完成它的所有不同方法种数的问题。
问题5:两个原理有怎样的共同点
和不同点
分类加法计数原理 分步乘法计数原理
完成一件事,共有n类办法,关键词“分类”
区别1
完成一件事,共分n个步骤,关键词 “分步”
区别2
区别3
每类办法都能独立地完成这件事情,它是独立的、一次的、且每次得到的是最后结果,只须一种方法就可完成这件事。
每一步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事。
各类办法是互斥的,并列的,独立的。
各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复.
例2:书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少种不同的取法?
解:
(1)从书架上任取一本书,有三类办法:
第1类办法是:从第1层取1本计算机书,有4种方法;
第2类办法是:从第2层取1本文艺书,有3种方法;
第3类办法是:从第3层取1本体育书,有2种方法;
根据分类加法计数原理,不同取法的种数是:
答:从书架上任取1本书,有9种不同的取法.
例2 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(2)从书架的第1,2,3层各取1本书,有多少种不同的取法?
解:
(2)从书架的1、2、3层各取1本书,可以分3步来完成:
第1步:从第1层取1本计算机书,有4种方法;
第2步:从第2层取1本文艺书,有3种方法;
第3步:从第3层取1本体育书,有2种方法;
根据分步乘法计数原理,从书架的1、2、3层各取1本书,不同取法的种数是:
答:从书架的1、2、3层各取1本书,有24种不同的取法。
例3 顺德区的部分电话号码是075722××××××,后面每个数字来自0-9这10个数,问可以产生多少个不同的电话号码
变式: 若要求最后6个数字不重复,则又有多少种不同的电话号码
075722
=151200
10
10
10
10
10
10
×
×
×
×
×
=106
分析:
分析:
10
9
8
7
6
5
×
×
×
×
×
例4:要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法
分步乘法计数原理:
3×2=6(种)
练一练:课本P7页.
课堂小结
两大原理:
(一)分类加法计数原理:
针对的是“分类”问题.各类方法相互独立。
(二)分步乘法计数原理:
针对的是“分步”问题。每步相互依存。
作业:
教研室P1~2页原理(1).
教学反思
本教学设计的宗旨是“以学生为本,一切为了学生的发展”,教学中创设了一系列的问题情境,以充分调动学生的积极性,在问题的牵引下去主动思考和探索来完成相关知识的学习.
分类加法计数原理
与
分步乘法计数原理
(二)
复习回顾:
请你说说分类加法计数原理和分步乘法计数原理分别是什么 它们的作用是什么 它们有怎样的区别
在幸运52中有种游戏,其中的一个环节是在给出的6道题中两位选手各自为对方选不同的一道题,则不同的结果会有多少种?
农业
旅游
商业
美术
数学
体育
课堂练习:
6×5=30(种)
为了对某农作物新品种选择最佳生产条件,在分别有3种不同土质,2种不同施肥量,4种不同种植密度,3种不同时间的因素下进行种植试验,则不同的实验方案共有多少种
乘法原理: 3×2×4×3=72(种)
课堂练习:
一个商店销售某种型号的电视机,其中本地的产品有4种,外地的产品有7种,要买1台这种型号的电视机,有多少种不同的选法?
课堂练习:
加法原理: N= 4 + 7 =11(种)
设有5副不同的油画,2副不同的国画,7副不同的水彩画。从这些油画、国画、水彩画中各选一副布置房间,有几种不同的选法?
课堂练习:
乘法原理: N=5×2 ×7 =70(种)
由数字1、2、3、4、5
(1)可以组成多少个不同的三位数?
(2)可以组成多少个没有重复数字的三位数
课堂练习:
N=5×5 ×5=125(个)
N=5×4×3=60(个)
我们班里有4名同学参加学校里的足球
队、篮球队、乒乓球队,每人限报其中
的1个运动队,不同的报名方法有多少种?
课堂练习:
乘法原理: N=3×3 ×3 × 3=81(种)
如图,从甲地到乙地有2条路,从乙地
到丁地有3条路;从甲地到丙地有4条路
可以走,从丙地到丁地有2条路。从甲
地到丁地共有多少种不同地走法?
课堂练习:
甲地
丙地
丁地
乙地
N1=2×3=6
N2=4×2=8
N= N1+N2 =14
例1: 一个三位密码锁,各位上数字由0,1,2,3,4,5,6,7,8,9十个数字组成, (1)可以设置多少种三位数的密码(各位上的数字允许重复)?
(2)首位数字不为0的密码数是多少?
(3)首位数字是0的密码数又是多少?
N1=10×10×10=1000(种)
N2=9×10×10=900(种)
N3=10×10=100(种)
例2.给程序模块命名,需要用3个字符,其中首个字符要求用字母A-G或U-Z,后两个要求用数字1-9,问最多可以给多少个程序命名?
N=13×9×9=1053(个)
点评: 分类原理中的“分类”要全面, 不能遗漏; 但也不能重复、交叉;“类”与“类之间是并列的、互斥的、独立的,也就是说,完成一件事情,每次只能选择其中的一类办法中的某一种方法。若完成某件事情有n类办法, 即它们两两的交为空集,n类的并为全集。
分步原理中的“分步”程序要正确。“步”与“步”之间是连续的,不间断的,缺一不可;但也不能重复、交叉;若完成某件事情需n步, 则必须且只需依次完成这n个步骤后,这件事情才算完成。
在运用“分类原理、分步原理”处理具体应用题时,除要弄清是“分类”还是“分步”外,还要搞清楚“分类”或“分步”的具体标准。在“分类”或“分步”过程中,标准必须一致,才能保证不重复、不遗漏。
例3.如图,该电路,从A到B共有多少条不同的线路可通电?
A
B
解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4 条
所以, 根据分类原理, 从A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
点评:
在解题时有时既要分类又要分步.
解:从总体上看,如,蚂蚁从顶点A爬到顶点C1有三类方法,从局部上看每类又需3步完成,所以,
第一类, m1 = 1×1×2 = 2 条
第二类, m2 = 1× 1×2 = 2 条
第三类, m3 = 1×1×2 = 2 条
所以, 根据加法原理, 从顶点A到顶点C1最近路线共有 N = 2 + 2 + 2 = 6 条。
练一练:一蚂蚁沿着长方体的棱,从的一个顶点爬到相对的另一个顶点的最近路线共有多少条?
课堂小结
应用两个原理求完成一件事的方法总数时,要注意:
(1)分清用加法原理还是乘法原理;
(2)有时既要分类又要分步,也就是说既要用到加法原理又要用到乘法原理,此时往往是先分类再分步.
作业:
1.课本P14-15页A组T3,T5;B组T1,T2.
2.教研室P2-3页原理(2).
教学反思:
1、教学中注重利用“延时评价”,尊重学生的个体差异,让学生发表自己的看法,从而调动、活跃学生的思维。
2、通过观察与学生交流采用肯定、赞扬、欣赏等鼓励性语言,激励和促进学生的发展。
3、通过游戏问题,鼓励学生大胆猜想,关注学生活动过程的表现,关注学生在活动中能否积极主动地参与讨论、发现、分析和解决问题。
分类加法计数原理
与
分步乘法计数原理
(三)
复习与回顾
复习两个计数原理:
例1(P7页例6)核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子?
U
U
U
A
A
A
C
C
C
G
G
G
4×4×…×4=4100(个)
100个4
例2(P8页例7).电子元件很容易实现电路的通与断、电位的高与底等两种状态,而这也是最容易控制的两种状态。因此计算机内部就采用了每一位只有0或1两种数字的计数法,即二进制,为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成,问(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)计算机汉字国标码(GB码)包含了6763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
2×2×2×2×2×2×2×2=28=256(个)
∵256×256=65536(个)>6763个∴至少2个字节.
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
例3(P9页例8).计算机编程人员在编写好程序以后要对程序进行测试。程序员需要知道到底有多少条执行路径(即程序从开始到结束的路线),以便知道需要提供多少个测试数据。一般的,一个程序模块又许多子模块组成,它的一个具有许多执行路径的程序模块。问:(1)这个程序模块有多少条执行路径?
(2)为了减少测试时间,程序员需要设法减少测试次数,你能帮助程序员设计一个测试方式,以减少测试次数吗?
例4(P11页例9).随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容。交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现,那么这种办法共能给多少辆汽车上牌照
分析:(1)先分类后分步: 26×25×24×10×9×8=11232000; 11232000+11232000=22464000(辆).
(2)分步: 26×25×24×10×9×8×2=11232000×2 =22464000(辆).
2.如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
课堂练习:
答案:6种.
若用2色、4色、5色等,结果又怎样呢?
答:它们的涂色方案种数分别是 0、 4×3×2×2 = 48、 5×4×3×3 = 180种等。
思考:
1.课本P12页练习.
课堂小结
1.两大原理:
(1)分类加法计数原理:
针对的是“分类”问题.各类方法相互独立。
(2)分步乘法计数原理:
针对的是“分步”问题。每步相互依存。
2.两大原理的区别.
3.在实际应用中,经常既要用到加法原理又要用到乘法原理,此时往往是先分类再分步.
作业:
教研室P3-4页原理(3).
教学反思
本教学是两个原理的综合应题,有一定的难度,教师要设计一系列问题来化难为易,让学生独立思考,鼓励学生独立解决.
分类加法计数原理
与
分步乘法计数原理
(一)
〖教学目的〗
1、知识与技能:分类与分步原理及其应用。
2、过程与方法:通过实例探究,找到两个记数原理,理解两个原理的内容。
3、情感态度与价值观:要求学生在现实生活中面对复杂的事物和现象,能够作出正确的分析和判断,进而拿出完善的处理方案,提高实际应变能力,从而认识数学知识与现实生活的内在联系
〖教学重点〗
归纳地得出分类加法计数原理和分步乘法计数原理,能应用它们解决简单的实际问题.
〖教学难点〗
正确理解“完成一件事情”的含义;根据实际问题的特征,正确地区分“分类”或“分步”.
问题1:用一个大写的的英文字母或一个阿拉伯数字给教室里的座位编号,总共能够编出多少种不同的号码?
26+10=36(种)
问题2:从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船.一天中,火车有4 班,汽车有2班,轮船有3班.那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法
分析: 从甲地到乙地有3类方法:
第一类方法, 乘火车,有4种方法;
第二类方法, 乘汽车,有2种方法;
第三类方法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有
4 + 2 + 3 = 9
种方法。
基础知识
一、分类加法计数原理
完成一件事,有n类办法. 在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,则完成这件事共有
种不同的方法。
N= m1+m2+… +mn
(加法原理)
弄清要完成哪件事情
类与类之间互不相容,各类中的方法也互不相同
例1:在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自已感兴趣的强项专业,具体情况如下: A大学 B大学 生物学 数学 化学 会计学 医学 信息技术学 物理学 法学 工程学 那么,这名同学可能的专业选择共有多少种
分类加法计数原理:5+4=9(种)
问题3:用前6个大写英文字母和1-9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少个不同的号码?
字母 数字 得到的号码
A
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
树形图
由于前6个英文字母中的任意一个都能与9个数字中的任何一个组成一个号码,而且它们各个不同,因此共有
6×9=54
个不同的号码.
问题3:用前6个大写英文字母和1-9九个阿拉伯数字,以A1,A2,···,B1,B2,···的方式给教室里的座位编号,总共能编出多少个不同的号码?
汽车有2班,那么两天中,从甲地到乙地共有多少种不同的走法?
所有走法:
如何计算所有不同走法的种数?
∵乘火车有3种走法,乘汽车有2种走法,
∴乘一次火车再换乘一次汽车从甲地到乙地,
共有3×2=6种不同的走法。
问题4:从甲地到乙地,要从甲地先乘火车到丙地,再于
次日从丙地乘汽车到乙地。
已知从一天中,火车有3班,
基础知识
二、分步乘法计数原理
完成一件事,需要分成n个步骤. 做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,则完成这件事共有
种不同的方法。
N= m1×m2×… ×mn
(乘法原理)
弄清要完成哪件事情
各步之间互相依存且做完任何一步所选用方法数与其他步骤所选用的方法无关.
分步加法计数原理和分类乘法计数原理的共同点:
计算做一件事情完成它的所有不同方法种数的问题。
问题5:两个原理有怎样的共同点
和不同点
分类加法计数原理 分步乘法计数原理
完成一件事,共有n类办法,关键词“分类”
区别1
完成一件事,共分n个步骤,关键词 “分步”
区别2
区别3
每类办法都能独立地完成这件事情,它是独立的、一次的、且每次得到的是最后结果,只须一种方法就可完成这件事。
每一步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事。
各类办法是互斥的,并列的,独立的。
各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复.
例2:书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1,2,3层各取1本书,有多少种不同的取法?
解:
(1)从书架上任取一本书,有三类办法:
第1类办法是:从第1层取1本计算机书,有4种方法;
第2类办法是:从第2层取1本文艺书,有3种方法;
第3类办法是:从第3层取1本体育书,有2种方法;
根据分类加法计数原理,不同取法的种数是:
答:从书架上任取1本书,有9种不同的取法.
例2 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书,
(2)从书架的第1,2,3层各取1本书,有多少种不同的取法?
解:
(2)从书架的1、2、3层各取1本书,可以分3步来完成:
第1步:从第1层取1本计算机书,有4种方法;
第2步:从第2层取1本文艺书,有3种方法;
第3步:从第3层取1本体育书,有2种方法;
根据分步乘法计数原理,从书架的1、2、3层各取1本书,不同取法的种数是:
答:从书架的1、2、3层各取1本书,有24种不同的取法。
例3 顺德区的部分电话号码是075722××××××,后面每个数字来自0-9这10个数,问可以产生多少个不同的电话号码
变式: 若要求最后6个数字不重复,则又有多少种不同的电话号码
075722
=151200
10
10
10
10
10
10
×
×
×
×
×
=106
分析:
分析:
10
9
8
7
6
5
×
×
×
×
×
例4:要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,问共有多少种不同的挂法
分步乘法计数原理:
3×2=6(种)
练一练:课本P7页.
课堂小结
两大原理:
(一)分类加法计数原理:
针对的是“分类”问题.各类方法相互独立。
(二)分步乘法计数原理:
针对的是“分步”问题。每步相互依存。
作业:
教研室P1~2页原理(1).
教学反思
本教学设计的宗旨是“以学生为本,一切为了学生的发展”,教学中创设了一系列的问题情境,以充分调动学生的积极性,在问题的牵引下去主动思考和探索来完成相关知识的学习.
分类加法计数原理
与
分步乘法计数原理
(二)
复习回顾:
请你说说分类加法计数原理和分步乘法计数原理分别是什么 它们的作用是什么 它们有怎样的区别
在幸运52中有种游戏,其中的一个环节是在给出的6道题中两位选手各自为对方选不同的一道题,则不同的结果会有多少种?
农业
旅游
商业
美术
数学
体育
课堂练习:
6×5=30(种)
为了对某农作物新品种选择最佳生产条件,在分别有3种不同土质,2种不同施肥量,4种不同种植密度,3种不同时间的因素下进行种植试验,则不同的实验方案共有多少种
乘法原理: 3×2×4×3=72(种)
课堂练习:
一个商店销售某种型号的电视机,其中本地的产品有4种,外地的产品有7种,要买1台这种型号的电视机,有多少种不同的选法?
课堂练习:
加法原理: N= 4 + 7 =11(种)
设有5副不同的油画,2副不同的国画,7副不同的水彩画。从这些油画、国画、水彩画中各选一副布置房间,有几种不同的选法?
课堂练习:
乘法原理: N=5×2 ×7 =70(种)
由数字1、2、3、4、5
(1)可以组成多少个不同的三位数?
(2)可以组成多少个没有重复数字的三位数
课堂练习:
N=5×5 ×5=125(个)
N=5×4×3=60(个)
我们班里有4名同学参加学校里的足球
队、篮球队、乒乓球队,每人限报其中
的1个运动队,不同的报名方法有多少种?
课堂练习:
乘法原理: N=3×3 ×3 × 3=81(种)
如图,从甲地到乙地有2条路,从乙地
到丁地有3条路;从甲地到丙地有4条路
可以走,从丙地到丁地有2条路。从甲
地到丁地共有多少种不同地走法?
课堂练习:
甲地
丙地
丁地
乙地
N1=2×3=6
N2=4×2=8
N= N1+N2 =14
例1: 一个三位密码锁,各位上数字由0,1,2,3,4,5,6,7,8,9十个数字组成, (1)可以设置多少种三位数的密码(各位上的数字允许重复)?
(2)首位数字不为0的密码数是多少?
(3)首位数字是0的密码数又是多少?
N1=10×10×10=1000(种)
N2=9×10×10=900(种)
N3=10×10=100(种)
例2.给程序模块命名,需要用3个字符,其中首个字符要求用字母A-G或U-Z,后两个要求用数字1-9,问最多可以给多少个程序命名?
N=13×9×9=1053(个)
点评: 分类原理中的“分类”要全面, 不能遗漏; 但也不能重复、交叉;“类”与“类之间是并列的、互斥的、独立的,也就是说,完成一件事情,每次只能选择其中的一类办法中的某一种方法。若完成某件事情有n类办法, 即它们两两的交为空集,n类的并为全集。
分步原理中的“分步”程序要正确。“步”与“步”之间是连续的,不间断的,缺一不可;但也不能重复、交叉;若完成某件事情需n步, 则必须且只需依次完成这n个步骤后,这件事情才算完成。
在运用“分类原理、分步原理”处理具体应用题时,除要弄清是“分类”还是“分步”外,还要搞清楚“分类”或“分步”的具体标准。在“分类”或“分步”过程中,标准必须一致,才能保证不重复、不遗漏。
例3.如图,该电路,从A到B共有多少条不同的线路可通电?
A
B
解: 从总体上看由A到B的通电线路可分三类,
第一类, m1 = 3 条
第二类, m2 = 1 条
第三类, m3 = 2×2 = 4 条
所以, 根据分类原理, 从A到B共有
N = 3 + 1 + 4 = 8
条不同的线路可通电。
点评:
在解题时有时既要分类又要分步.
解:从总体上看,如,蚂蚁从顶点A爬到顶点C1有三类方法,从局部上看每类又需3步完成,所以,
第一类, m1 = 1×1×2 = 2 条
第二类, m2 = 1× 1×2 = 2 条
第三类, m3 = 1×1×2 = 2 条
所以, 根据加法原理, 从顶点A到顶点C1最近路线共有 N = 2 + 2 + 2 = 6 条。
练一练:一蚂蚁沿着长方体的棱,从的一个顶点爬到相对的另一个顶点的最近路线共有多少条?
课堂小结
应用两个原理求完成一件事的方法总数时,要注意:
(1)分清用加法原理还是乘法原理;
(2)有时既要分类又要分步,也就是说既要用到加法原理又要用到乘法原理,此时往往是先分类再分步.
作业:
1.课本P14-15页A组T3,T5;B组T1,T2.
2.教研室P2-3页原理(2).
教学反思:
1、教学中注重利用“延时评价”,尊重学生的个体差异,让学生发表自己的看法,从而调动、活跃学生的思维。
2、通过观察与学生交流采用肯定、赞扬、欣赏等鼓励性语言,激励和促进学生的发展。
3、通过游戏问题,鼓励学生大胆猜想,关注学生活动过程的表现,关注学生在活动中能否积极主动地参与讨论、发现、分析和解决问题。
分类加法计数原理
与
分步乘法计数原理
(三)
复习与回顾
复习两个计数原理:
例1(P7页例6)核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子?
U
U
U
A
A
A
C
C
C
G
G
G
4×4×…×4=4100(个)
100个4
例2(P8页例7).电子元件很容易实现电路的通与断、电位的高与底等两种状态,而这也是最容易控制的两种状态。因此计算机内部就采用了每一位只有0或1两种数字的计数法,即二进制,为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用一个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成,问(1)一个字节(8位)最多可以表示多少个不同的字符?
(2)计算机汉字国标码(GB码)包含了6763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示?
2×2×2×2×2×2×2×2=28=256(个)
∵256×256=65536(个)>6763个∴至少2个字节.
开始
子模块1
18条执行路径
子模块3
28条执行路径
子模块2
45条执行路径
子模块5
43条执行路径
子模块4
38条执行路径
结束
A
例3(P9页例8).计算机编程人员在编写好程序以后要对程序进行测试。程序员需要知道到底有多少条执行路径(即程序从开始到结束的路线),以便知道需要提供多少个测试数据。一般的,一个程序模块又许多子模块组成,它的一个具有许多执行路径的程序模块。问:(1)这个程序模块有多少条执行路径?
(2)为了减少测试时间,程序员需要设法减少测试次数,你能帮助程序员设计一个测试方式,以减少测试次数吗?
例4(P11页例9).随着人们生活水平的提高,某城市家庭汽车拥有量迅速增长,汽车牌照号码需要扩容。交通管理部门出台了一种汽车牌照组成办法,每一个汽车牌照都必须有3个不重复的英文字母和3个不重复的阿拉伯数字,并且3个字母必须合成一组出现,3个数字也必须合成一组出现,那么这种办法共能给多少辆汽车上牌照
分析:(1)先分类后分步: 26×25×24×10×9×8=11232000; 11232000+11232000=22464000(辆).
(2)分步: 26×25×24×10×9×8×2=11232000×2 =22464000(辆).
2.如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
课堂练习:
答案:6种.
若用2色、4色、5色等,结果又怎样呢?
答:它们的涂色方案种数分别是 0、 4×3×2×2 = 48、 5×4×3×3 = 180种等。
思考:
1.课本P12页练习.
课堂小结
1.两大原理:
(1)分类加法计数原理:
针对的是“分类”问题.各类方法相互独立。
(2)分步乘法计数原理:
针对的是“分步”问题。每步相互依存。
2.两大原理的区别.
3.在实际应用中,经常既要用到加法原理又要用到乘法原理,此时往往是先分类再分步.
作业:
教研室P3-4页原理(3).
教学反思
本教学是两个原理的综合应题,有一定的难度,教师要设计一系列问题来化难为易,让学生独立思考,鼓励学生独立解决.
