北京市11学校2022届高三上学期8月学习检测数学试题 Word版含答案
文档属性
| 名称 | 北京市11学校2022届高三上学期8月学习检测数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览




文档简介
北京市十一学校2022届高三学习检测
数学20210812
满分:150分
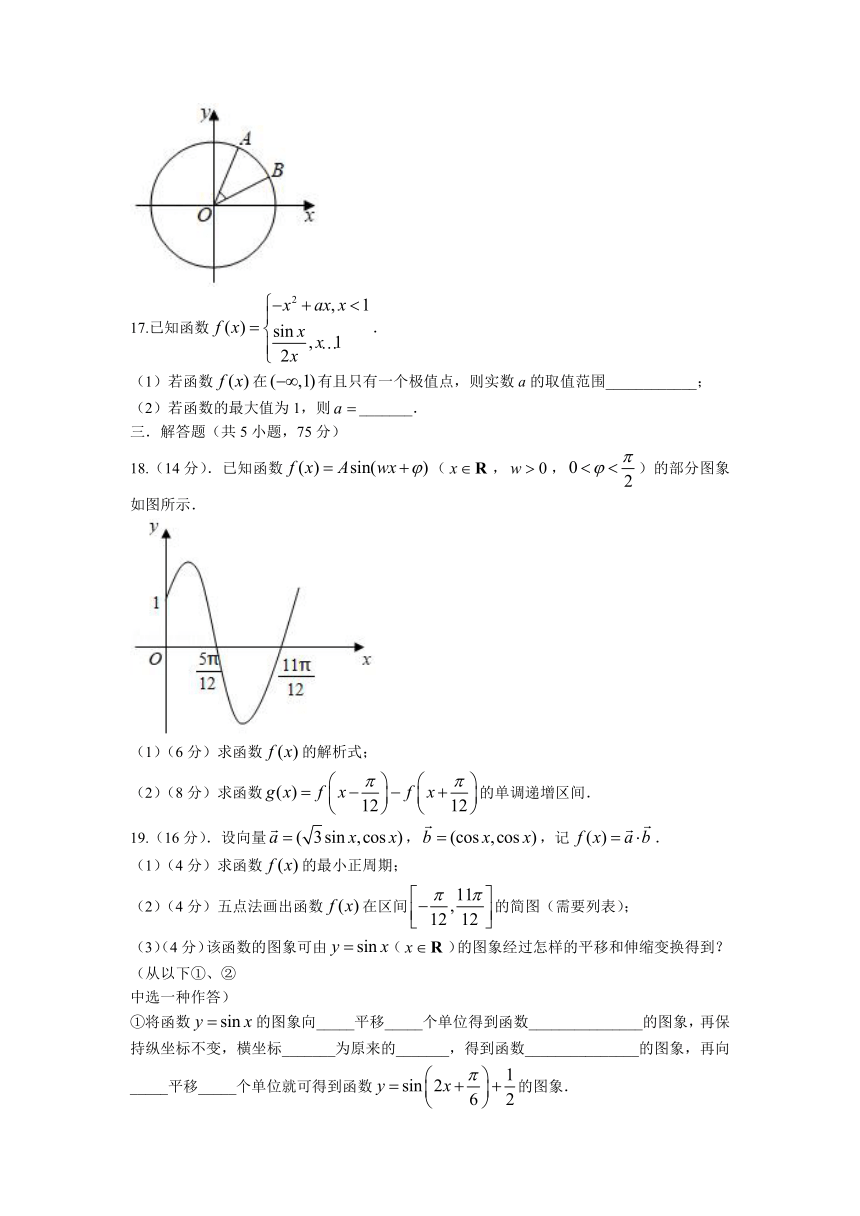
时间:120分钟
一、选择题(每小题4分,共40分.在每小题的四个选项中,选出符合题目要求的一项)
1.设集合,,,则(
)
A.
B.
C.
D.
2.命题“,”的否定是(
)
A.,
B.,
C.,
D.,
3.已知为第二象限角,且,则的值是(
)
A.
B.
C.
D.
4.最小正周期为,且图象关于直线对称的一个函数是(
)
A.
B.
C.
D.
5.如图,在中,D,E,F分别为线段,,的中点,则(
)
A.
B.
C.
D.
6.已知向量,不共线,且,,若与反向共线,则实数值为(
)
A.1
B.
C.1或
D.-1或
7.若a,,则“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
8.已知函数,若方程有且只有两个不相等的实数根,则实数a的取值
范围是(
)
A.
B.
C.
D.
9.所谓声强,是指声音在传播途径上每1平方米面积上的声能流密度,用I表示人类能听到的声强范围,其中能听见的1000声音的声强(约)为标准声强,记作,声强I与标准声强之比的常用对数称作声强的声强级,记作L,即,声强级L的单位名称为贝(尔),符号为B,取贝(尔)的十分之一作为响度的常用单位,称为分贝(尔).简称分贝().《三国演义》中有张飞喝断当阳桥的故事,设张飞大喝一声的响度为140.一个士兵大喝一声的响度为90,如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群士兵的人数为(
)
A.1万
B.2万
C.5万
D.10万
10.已知函数的定义域为,若存在常数,对任意,有,则称为F函数.给出下列函数:①;②;③;④是定义在上的奇函数,且满足对一切实数,均有.其中是F函数的序号为(
)
A.②④
B.①③
C.③④
D.①②
二.填空题(共7个小题,每小题5分,共35分;15-16-17题前一空3分,后一空2分)
11.已知(a,)是的共轭复数,则______.
12.已知幂函数的图象经过点,则______.
13.若扇形的周长是8,面积24,则扇形的圆心角为______.
14.已知非零向量,满足,且,则与的夹角为________.
15.已知a,b为正实数,直线与曲线相切,则a与b满足的关系式为________,的最小值为________.
16.如图,在平面直角坐标系中,以轴为始边做两个锐角,,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为,.则的值为________;的值为________.
17.已知函数.
(1)若函数在有且只有一个极值点,则实数a的取值范围____________;
(2)若函数的最大值为1,则_______.
三.解答题(共5小题,75分)
18.(14分).已知函数(,,)的部分图象如图所示.
(1)(6分)求函数的解析式;
(2)(8分)求函数的单调递增区间.
19.(16分).设向量,,记.
(1)(4分)求函数的最小正周期;
(2)(4分)五点法画出函数在区间的简图(需要列表);
(3)(4分)该函数的图象可由()的图象经过怎样的平移和伸缩变换得到?(从以下①、②
中选一种作答)
①将函数的图象向_____平移_____个单位得到函数_______________的图象,再保持纵坐标不变,横坐标_______为原来的_______,得到函数_______________的图象,再向_____平移_____个单位就可得到函数的图象.
②将函数的图象上的点纵坐标不变,横坐标________为原来的_______,得到函数_____________的图象,再向_____平移_____个单位得到函数_______________的图象,再向_____平移_____个单位得到函数的图象.
(4)(4分)若时,函数的最小值为2,试求出函数的最大值并指出取何值时,函数取得最大值.
20.(15分).已知:函数().
(1)(4分)若,求曲线在点处的切线方程;
(2)(5分)求函数的单调区间;
(3)(6分)函数在区间上满足,求a的取值范围.
21.(15分).已知函数,().
(1)(5分)若时,求函数的最小值;
(2)(5分)若,证明:函数有且只有一个零点;
(3)(5分)若函数有两个零点,求实数a的取值范围.
22.(15分)已知集合(),对于,,定义A与B的差为;A与B之间的距离为.
(1)(4分)若,试写出所有可能的A,B;
(2)(4分),证明:;
(3)(7分),,,三个数中是否一定有偶数?证明你的结论.
北京市十一学校2022届高三学习检测答案
数学20210812
一、选择题(共10小题,每小题4分,共40分)
1.解:集合B中的不等式,变形得:,
解得:,∴,∵,∴,
∵集合,∴.故选:D.
2.解:因为全称命题的否定是特称命题,
所以命题p:,,则为,.故选:A.
3.解:∵为第二象限角,,∴,∴,则.故选:D.
4.解:由于函数的最小正周期为,故排除A;
由于函数的最小正周期为,当时,,不是最值,故函数的图象不关于直线对称,故排除B;
由于函数的最小正周期为,当时,,是最大值,故函数的图象关于直线对称,故C正确;
由于函数的最小正周期为,当时,,不是最值,故函数的图象不关于直线对称,故排除D,
故选:C.
5.解:∵,
故选:D.
6.解:据题意向量,不共线,且,,若与反向,
存在m()使得,即,
∵,不共线,∴,∴.故选:B.
7.解:方法1:,又与同号,,∴“”是“”的充要条件.
方法2:,,当且仅当时取等号.
∴,“”.
∴“”是“”的充要条件.故选:C.
8.解:当时,,
同理,当时,,……,
所以函数的图象如图所示,
当时,函数的图象与函数的图象有两个交点,
即方程有且只有两个不相等的实数根.
故选:A.
9.解:由题意得,解得张飞大喝一声的声强为:(),
每一个士兵大喝一声的声强为:(),
∵,
∴如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群士兵的人数为10万.故选:D.
10.解:对于①,,显然不成立,故其不是F函数;
对于②,,由于时,不成立,故不是F函数;
对于③,,,故对任意的,都有,故其是F函数;
对于④,是定义在上的奇函数,且满足对一切实数,均有,令,,由奇函数的性质知,,故有.显然是F函数
故选:C.
二、填空题(共7个小题,每小题5分,共35分;15-16-17前一空3分,后一空2分)
11.1
解:,∴,∴,,∴,
12.
解:设,因为幂函数图象过,则有,∴,即,
∴.
13.2
解:设扇形的圆心角为,半径为R,则.故答案为:2.
14.
解:根据题意,设与的夹角为,,则,
若,则,
变形可得:,又由,则,故答案为:.
15.,
解:由,得,因此曲线在切点处的切线的斜率等于2,
∴,即,此时.则切点为,
相应的切线方程为,
则,∴.
又,,∴.
当且仅当时上式等号成立.
故答案为:;.
16.7,
解:已知,,,
则,则,
,则,
则,则,
∵t,∴,∵,∴,
则,则.
故答案为:7,.
17.(1)
(2)-2
解:(1)时,,,若在有且只有一个极值点,则在上有解,故;
(2)时,的对称轴是,
①即时,在递增,,函数无最大值
②即时,在递增,在递减,
故,解得:或(舍);
时,,
综上,
故答案为:,-2.
三、解答题(共5小题,75分)
18(14分).解:(1)由图可知,可得,则,则;
…………2’
又图象经过,故有,,得;
又,取.
…………4’
过点,所以,可得.
得.
…………6’
(2)
…………2’
…………4’
,
…………5’
由,,
…………6’
得,,
所以的单调递增区间为,.
…………8’
注:1.单调区间不是区间形式的答案,减1分;忽略,减1分;化简到后,没有求单调区间的过程,只有最后单调区间答案的减2分;
2.考查三角函数的单调区间,一定是化成的形式,结合正弦函数的单调区间求得;不必采用导数的办法;
19(16分).解:(1)由题意可得:
…………2’(两个二倍角公式各1分)
…………3’
所以最小正周期.
…………4’
(2)表2分
x
0
(3)①左,,,缩短,,,,
②缩短,,,左,,,
从第一个空开始算,对一个空0.5分,总分向下取整。(如出现实质性错误,从该空及后面的空均不给分,如平移方向、单位个数错误)。
(4)方法一:
由,可得,所以,进而可得.
又因为函数的最小值为2,所以.
…………2’
所以
当时,即时,函数取得最大值.…………4’(等号成立的条件及由来、最值各1分)
方法二:
因为在上单调递增,在上单调递减,且,,
所以的最小值为m,所以.
…………6’
所以
当时,即时,函数取得最大值.………8’(等号成立的条件及由来、最值各1分)
20.解:(1)若,则,,
…………1’
所以,即切线的斜率等于—2;
…………2’
又,切点为;
…………3’
所以曲线在点处的切线方程为,即;…………4’
(2)的定义域为,
…………1’
(),
…………2’
当或时,,在和上单调递减;
当时,,在单调递增;
…………4’(列表和文字说明均可)
所以的递减区间为,;递增区间为;…………5’
(3)方法一:①当,即时,在上单调递增,,
解得,因此;
…………1’
②当,即时,在上单调递减,上单调递增,
,解得,因此;
…………3’
③当,与矛盾,因此无解;
…………4’
注:或者由于在要有定义,排除情况也可以;但写不给分
④当,在上单调递减,
,与矛盾,因此无解;
…………5’
综上所述,a的取值范围为.
…………6’
方法二:,()恒成立()恒成立,
①当时,,由,得,
令(),则,
故在区间上单调递增,,
所以,即,于是;
…………2’
②当时,,由得,
即,与矛盾;
…………4’
③当时,恒成立,符号不确定,故不符合题意;…………5’
综上所述,a的取值范围为.
…………6’
方法三:∵,()恒成立,,
所以,有,所以.
…………2’
所以,()恒成立恒成立,
所以
…………3’
令(),则,
故在区间上单调递增,,
所以,即,于是;
…………5’
所以a的取值范围为.
…………6’
方法四:∵,()恒成立,
因此,即,所以.
…………2’
当,即时,
由(2)知,在上单调递减,上单调递增,
恒成立,
因此符合题意;
…………4’
当时,由(2)知,在上单调递增,恒成立,
因此符合题意;
…………5’
综上所述,a的取值范围为.
…………6’
21.解:(1)当时,,∴().………1’
令,得,
…………2’
当时,;当时,,
…………3’
∴函数在上单调递减,在上单调递增,
…………4’
∴当时,有最小值;
…………5’
注:有的同学只写导数的正负,不写单调性,扣1分,这里还是建议画表格,导数符号和单调性都有了
(2)证明:由,得(),…………1’
∴当时,,函数在上单调递减,
…………2’
∴当时,在上最多有一个零点.
又当时,,
…………3’
,
…………4’
∴当时,函数在上有零点.…………5’
综上,当时,函数有且只有一个零点;
注:有的同学只说函数单调递减,没有分别找出函数值大于0和小于0的自变量,这是不可以的,因为不符合零点存在定理的条件,这样扣2分,找其他的能确认正负的值都可以得分;还有的同学用到了极限,扣1分
(3)方法一:令,(),
所以(),设();
…………1’
函数有两个零点,必须函数与的图象有两个交点.
,设,显然与的符号相同,
又在上单调递减,且;
所以当时,,,在上单调递增;
…………2’
当时,,,在上单调递减;
…………3’
∴函数的极大值为,又,
当时,,且当时,,
…………4’
所以,函数有两个零点,必须.
…………5’
注:有的同学看到(2)(3)两问都是关于函数零点的问题,因此就都用的参变分离的方法,这是极好的,极大地降低了难度
方法二:由(2)知,当时,在上单调递减,最多有一个零点.
∵有两个零点,∴.
由,得().令,
∵,,∴在上只有一个零点,设这个零点为(其中),
…………1’
当时,,,函数在上单调递减;
…………2’
当时,,,函数在上单调递增.
…………3’
要使函数在上有两个零点,必须函数的极小值,即.
∵2,∴,
又∵在上是减函数,且,
∴,即,解得;…………4’
此时,当时,;
∵,∴,
当时,,∴;
所以当时,函数有两个零点.
…………5’
或者下面这样说明:
当时,,,∴.
∵,且,∴函数在上有一个零点.
又∵,∴,
且,在上有一个零点.
∴当时,函数在内有两个零点.
综上,实数a的取值范围是.
22.解:(1),;
…………1’
,;
…………2’
,;
…………3’
,.
…………4’
(2)令,,,对,2,…,n,
;
…………1’
方法一:
显然当时,;当时,;
当时,有;
…………2’
当时,有.
…………3’
所以
………4’
方法二:
0
0
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
由表可知
…………3’
所以
………4’
(3),,,三个数中一定有偶数.
…………1’
理由如下:
方法一:
由于,,只能取0或1,所以,,中至少有两个相等,不妨设,此时
为偶数,
…………4’
故,,为偶数,
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.
…………7’
方法二:
因为,
且与奇偶性相同.…………3’
所以为偶数,
故为偶数,…………5’
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.…………7’
方法三:
0
0
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
1
0
0
1
1
0
1
0
0
1
0
1
0
1
1
0
1
0
0
0
1
1
0
0
1
1
0
2
2
2
2
0
2
2
由表可知必为偶数,
…………4’
则
必为偶数
…………5’
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.
…………7’
方法四:
两整数x、y,与奇偶性相同
则与||+奇偶性相同,
与奇偶性相同,
即与奇偶性相同
…………3’
由(2)可知
…………4’
所以与奇偶性相同,必为偶数
…………5’
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.
…………7’
数学20210812
满分:150分
时间:120分钟
一、选择题(每小题4分,共40分.在每小题的四个选项中,选出符合题目要求的一项)
1.设集合,,,则(
)
A.
B.
C.
D.
2.命题“,”的否定是(
)
A.,
B.,
C.,
D.,
3.已知为第二象限角,且,则的值是(
)
A.
B.
C.
D.
4.最小正周期为,且图象关于直线对称的一个函数是(
)
A.
B.
C.
D.
5.如图,在中,D,E,F分别为线段,,的中点,则(
)
A.
B.
C.
D.
6.已知向量,不共线,且,,若与反向共线,则实数值为(
)
A.1
B.
C.1或
D.-1或
7.若a,,则“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
8.已知函数,若方程有且只有两个不相等的实数根,则实数a的取值
范围是(
)
A.
B.
C.
D.
9.所谓声强,是指声音在传播途径上每1平方米面积上的声能流密度,用I表示人类能听到的声强范围,其中能听见的1000声音的声强(约)为标准声强,记作,声强I与标准声强之比的常用对数称作声强的声强级,记作L,即,声强级L的单位名称为贝(尔),符号为B,取贝(尔)的十分之一作为响度的常用单位,称为分贝(尔).简称分贝().《三国演义》中有张飞喝断当阳桥的故事,设张飞大喝一声的响度为140.一个士兵大喝一声的响度为90,如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群士兵的人数为(
)
A.1万
B.2万
C.5万
D.10万
10.已知函数的定义域为,若存在常数,对任意,有,则称为F函数.给出下列函数:①;②;③;④是定义在上的奇函数,且满足对一切实数,均有.其中是F函数的序号为(
)
A.②④
B.①③
C.③④
D.①②
二.填空题(共7个小题,每小题5分,共35分;15-16-17题前一空3分,后一空2分)
11.已知(a,)是的共轭复数,则______.
12.已知幂函数的图象经过点,则______.
13.若扇形的周长是8,面积24,则扇形的圆心角为______.
14.已知非零向量,满足,且,则与的夹角为________.
15.已知a,b为正实数,直线与曲线相切,则a与b满足的关系式为________,的最小值为________.
16.如图,在平面直角坐标系中,以轴为始边做两个锐角,,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为,.则的值为________;的值为________.
17.已知函数.
(1)若函数在有且只有一个极值点,则实数a的取值范围____________;
(2)若函数的最大值为1,则_______.
三.解答题(共5小题,75分)
18.(14分).已知函数(,,)的部分图象如图所示.
(1)(6分)求函数的解析式;
(2)(8分)求函数的单调递增区间.
19.(16分).设向量,,记.
(1)(4分)求函数的最小正周期;
(2)(4分)五点法画出函数在区间的简图(需要列表);
(3)(4分)该函数的图象可由()的图象经过怎样的平移和伸缩变换得到?(从以下①、②
中选一种作答)
①将函数的图象向_____平移_____个单位得到函数_______________的图象,再保持纵坐标不变,横坐标_______为原来的_______,得到函数_______________的图象,再向_____平移_____个单位就可得到函数的图象.
②将函数的图象上的点纵坐标不变,横坐标________为原来的_______,得到函数_____________的图象,再向_____平移_____个单位得到函数_______________的图象,再向_____平移_____个单位得到函数的图象.
(4)(4分)若时,函数的最小值为2,试求出函数的最大值并指出取何值时,函数取得最大值.
20.(15分).已知:函数().
(1)(4分)若,求曲线在点处的切线方程;
(2)(5分)求函数的单调区间;
(3)(6分)函数在区间上满足,求a的取值范围.
21.(15分).已知函数,().
(1)(5分)若时,求函数的最小值;
(2)(5分)若,证明:函数有且只有一个零点;
(3)(5分)若函数有两个零点,求实数a的取值范围.
22.(15分)已知集合(),对于,,定义A与B的差为;A与B之间的距离为.
(1)(4分)若,试写出所有可能的A,B;
(2)(4分),证明:;
(3)(7分),,,三个数中是否一定有偶数?证明你的结论.
北京市十一学校2022届高三学习检测答案
数学20210812
一、选择题(共10小题,每小题4分,共40分)
1.解:集合B中的不等式,变形得:,
解得:,∴,∵,∴,
∵集合,∴.故选:D.
2.解:因为全称命题的否定是特称命题,
所以命题p:,,则为,.故选:A.
3.解:∵为第二象限角,,∴,∴,则.故选:D.
4.解:由于函数的最小正周期为,故排除A;
由于函数的最小正周期为,当时,,不是最值,故函数的图象不关于直线对称,故排除B;
由于函数的最小正周期为,当时,,是最大值,故函数的图象关于直线对称,故C正确;
由于函数的最小正周期为,当时,,不是最值,故函数的图象不关于直线对称,故排除D,
故选:C.
5.解:∵,
故选:D.
6.解:据题意向量,不共线,且,,若与反向,
存在m()使得,即,
∵,不共线,∴,∴.故选:B.
7.解:方法1:,又与同号,,∴“”是“”的充要条件.
方法2:,,当且仅当时取等号.
∴,“”.
∴“”是“”的充要条件.故选:C.
8.解:当时,,
同理,当时,,……,
所以函数的图象如图所示,
当时,函数的图象与函数的图象有两个交点,
即方程有且只有两个不相等的实数根.
故选:A.
9.解:由题意得,解得张飞大喝一声的声强为:(),
每一个士兵大喝一声的声强为:(),
∵,
∴如果一群士兵同时大喝一声相当一张飞大喝一声的响度,那么这群士兵的人数为10万.故选:D.
10.解:对于①,,显然不成立,故其不是F函数;
对于②,,由于时,不成立,故不是F函数;
对于③,,,故对任意的,都有,故其是F函数;
对于④,是定义在上的奇函数,且满足对一切实数,均有,令,,由奇函数的性质知,,故有.显然是F函数
故选:C.
二、填空题(共7个小题,每小题5分,共35分;15-16-17前一空3分,后一空2分)
11.1
解:,∴,∴,,∴,
12.
解:设,因为幂函数图象过,则有,∴,即,
∴.
13.2
解:设扇形的圆心角为,半径为R,则.故答案为:2.
14.
解:根据题意,设与的夹角为,,则,
若,则,
变形可得:,又由,则,故答案为:.
15.,
解:由,得,因此曲线在切点处的切线的斜率等于2,
∴,即,此时.则切点为,
相应的切线方程为,
则,∴.
又,,∴.
当且仅当时上式等号成立.
故答案为:;.
16.7,
解:已知,,,
则,则,
,则,
则,则,
∵t,∴,∵,∴,
则,则.
故答案为:7,.
17.(1)
(2)-2
解:(1)时,,,若在有且只有一个极值点,则在上有解,故;
(2)时,的对称轴是,
①即时,在递增,,函数无最大值
②即时,在递增,在递减,
故,解得:或(舍);
时,,
综上,
故答案为:,-2.
三、解答题(共5小题,75分)
18(14分).解:(1)由图可知,可得,则,则;
…………2’
又图象经过,故有,,得;
又,取.
…………4’
过点,所以,可得.
得.
…………6’
(2)
…………2’
…………4’
,
…………5’
由,,
…………6’
得,,
所以的单调递增区间为,.
…………8’
注:1.单调区间不是区间形式的答案,减1分;忽略,减1分;化简到后,没有求单调区间的过程,只有最后单调区间答案的减2分;
2.考查三角函数的单调区间,一定是化成的形式,结合正弦函数的单调区间求得;不必采用导数的办法;
19(16分).解:(1)由题意可得:
…………2’(两个二倍角公式各1分)
…………3’
所以最小正周期.
…………4’
(2)表2分
x
0
(3)①左,,,缩短,,,,
②缩短,,,左,,,
从第一个空开始算,对一个空0.5分,总分向下取整。(如出现实质性错误,从该空及后面的空均不给分,如平移方向、单位个数错误)。
(4)方法一:
由,可得,所以,进而可得.
又因为函数的最小值为2,所以.
…………2’
所以
当时,即时,函数取得最大值.…………4’(等号成立的条件及由来、最值各1分)
方法二:
因为在上单调递增,在上单调递减,且,,
所以的最小值为m,所以.
…………6’
所以
当时,即时,函数取得最大值.………8’(等号成立的条件及由来、最值各1分)
20.解:(1)若,则,,
…………1’
所以,即切线的斜率等于—2;
…………2’
又,切点为;
…………3’
所以曲线在点处的切线方程为,即;…………4’
(2)的定义域为,
…………1’
(),
…………2’
当或时,,在和上单调递减;
当时,,在单调递增;
…………4’(列表和文字说明均可)
所以的递减区间为,;递增区间为;…………5’
(3)方法一:①当,即时,在上单调递增,,
解得,因此;
…………1’
②当,即时,在上单调递减,上单调递增,
,解得,因此;
…………3’
③当,与矛盾,因此无解;
…………4’
注:或者由于在要有定义,排除情况也可以;但写不给分
④当,在上单调递减,
,与矛盾,因此无解;
…………5’
综上所述,a的取值范围为.
…………6’
方法二:,()恒成立()恒成立,
①当时,,由,得,
令(),则,
故在区间上单调递增,,
所以,即,于是;
…………2’
②当时,,由得,
即,与矛盾;
…………4’
③当时,恒成立,符号不确定,故不符合题意;…………5’
综上所述,a的取值范围为.
…………6’
方法三:∵,()恒成立,,
所以,有,所以.
…………2’
所以,()恒成立恒成立,
所以
…………3’
令(),则,
故在区间上单调递增,,
所以,即,于是;
…………5’
所以a的取值范围为.
…………6’
方法四:∵,()恒成立,
因此,即,所以.
…………2’
当,即时,
由(2)知,在上单调递减,上单调递增,
恒成立,
因此符合题意;
…………4’
当时,由(2)知,在上单调递增,恒成立,
因此符合题意;
…………5’
综上所述,a的取值范围为.
…………6’
21.解:(1)当时,,∴().………1’
令,得,
…………2’
当时,;当时,,
…………3’
∴函数在上单调递减,在上单调递增,
…………4’
∴当时,有最小值;
…………5’
注:有的同学只写导数的正负,不写单调性,扣1分,这里还是建议画表格,导数符号和单调性都有了
(2)证明:由,得(),…………1’
∴当时,,函数在上单调递减,
…………2’
∴当时,在上最多有一个零点.
又当时,,
…………3’
,
…………4’
∴当时,函数在上有零点.…………5’
综上,当时,函数有且只有一个零点;
注:有的同学只说函数单调递减,没有分别找出函数值大于0和小于0的自变量,这是不可以的,因为不符合零点存在定理的条件,这样扣2分,找其他的能确认正负的值都可以得分;还有的同学用到了极限,扣1分
(3)方法一:令,(),
所以(),设();
…………1’
函数有两个零点,必须函数与的图象有两个交点.
,设,显然与的符号相同,
又在上单调递减,且;
所以当时,,,在上单调递增;
…………2’
当时,,,在上单调递减;
…………3’
∴函数的极大值为,又,
当时,,且当时,,
…………4’
所以,函数有两个零点,必须.
…………5’
注:有的同学看到(2)(3)两问都是关于函数零点的问题,因此就都用的参变分离的方法,这是极好的,极大地降低了难度
方法二:由(2)知,当时,在上单调递减,最多有一个零点.
∵有两个零点,∴.
由,得().令,
∵,,∴在上只有一个零点,设这个零点为(其中),
…………1’
当时,,,函数在上单调递减;
…………2’
当时,,,函数在上单调递增.
…………3’
要使函数在上有两个零点,必须函数的极小值,即.
∵2,∴,
又∵在上是减函数,且,
∴,即,解得;…………4’
此时,当时,;
∵,∴,
当时,,∴;
所以当时,函数有两个零点.
…………5’
或者下面这样说明:
当时,,,∴.
∵,且,∴函数在上有一个零点.
又∵,∴,
且,在上有一个零点.
∴当时,函数在内有两个零点.
综上,实数a的取值范围是.
22.解:(1),;
…………1’
,;
…………2’
,;
…………3’
,.
…………4’
(2)令,,,对,2,…,n,
;
…………1’
方法一:
显然当时,;当时,;
当时,有;
…………2’
当时,有.
…………3’
所以
………4’
方法二:
0
0
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
1
0
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
由表可知
…………3’
所以
………4’
(3),,,三个数中一定有偶数.
…………1’
理由如下:
方法一:
由于,,只能取0或1,所以,,中至少有两个相等,不妨设,此时
为偶数,
…………4’
故,,为偶数,
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.
…………7’
方法二:
因为,
且与奇偶性相同.…………3’
所以为偶数,
故为偶数,…………5’
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.…………7’
方法三:
0
0
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
1
0
0
1
1
0
1
0
0
1
0
1
0
1
1
0
1
0
0
0
1
1
0
0
1
1
0
2
2
2
2
0
2
2
由表可知必为偶数,
…………4’
则
必为偶数
…………5’
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.
…………7’
方法四:
两整数x、y,与奇偶性相同
则与||+奇偶性相同,
与奇偶性相同,
即与奇偶性相同
…………3’
由(2)可知
…………4’
所以与奇偶性相同,必为偶数
…………5’
所以,,三个数不可能都是奇数,
即,,三个数中一定有偶数.
…………7’
同课章节目录
