1.1.2《集合的基本关系》课件(新人教A版必修1)
文档属性
| 名称 | 1.1.2《集合的基本关系》课件(新人教A版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-17 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
观察以下几组集合,并指出它们元
素间的关系:
① A={1,2,3}, B={1,2,3,4,5};
② A={x|x>1}, B={x|x2>1};
③ A={四边形}, B={多边形};
④ A={x|x-3=0}, B={x|x > 2} .
集合A的元素都在B中!
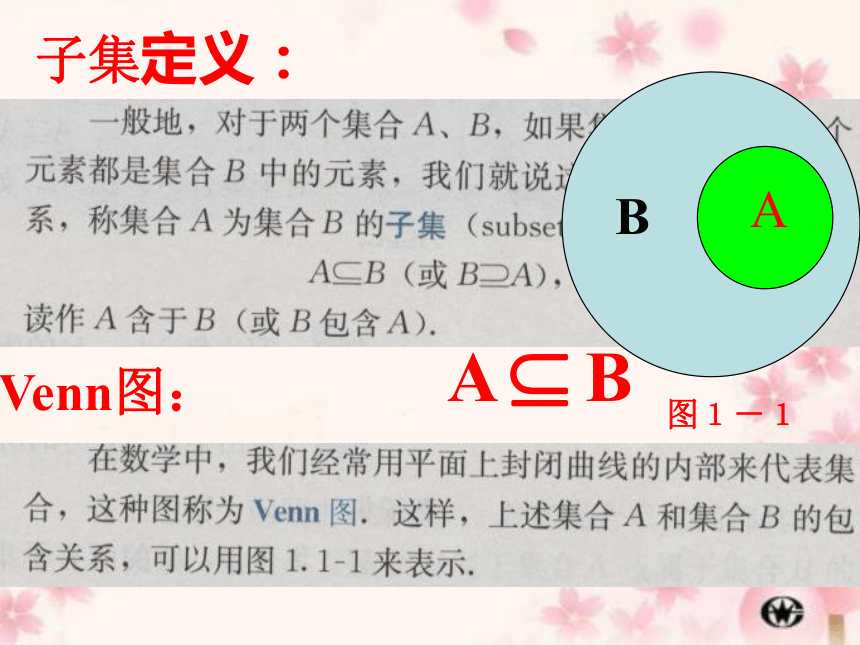
子集定义:
Venn图:
B
A B
A
图1-1
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
×
×
√
√
集合相等定义:
若A B且B A,
则A=B;
反之,亦然.
观察集合A与集合B的关系:
(1)A={1,3,5}, B={1,2,3,4,5,6}
(2) A={四边形}, B={多边形}
A B
A B
(1) A={a,b,c,d}, B={d,b,c,a}
(2) A={-1,1}, B={x x2-1=0}
观察集合A与集合B的关系:
A = B
A =B
B
A
图中A是否为B的子集
(1)
B
A
(2)
A不是B的子集
⑴ 集合A不包含于集合B,或集合B不包含集合A时,
记作 A B 或B A
注 意
⑵ 空集:我们把不含任何元素的集合叫做空集,记作:
A
规定:空集是任何集合的子集.
即对任何集合A,都有:
真子集定义:
图示为
A
B
观察集合A与集合B的关系:
(1)A={1,3,5}, B={1,2,3,4,5,6}
(2) A={四边形}, B={多边形}
子集的性质
(1)对任何集合A,都有:
A A
(2)对于集合A,B,C,若A B,且B
C,则有 A C
(3)空集是任何非空集合的真子集.
例题讲解
例1 写出{0,1,2}的所有子集,并指出其中哪些是它的真子集.
解:{0,1,2}的所有子集为:
{0}
{1}
{2}
{0,1}
{0, 2}
{1,2}
{0,1,2}
{0,1,2}的所有真子集为:
{0}
{1}
{2}
{0,1}
{0, 2}
{1,2}
例题讲解
例2 设A={x,x2,xy}, B={1,x,y},且A=B,求实数x,y的值.
解:∵{x,x2,xy}={1,x,y},
∴x2=1且xy=y,
或x2= y或 xy=1,
∴x=-1,y=0
例题讲解
例3 若A={x |-3≤x≤4}, B={x|2m-1≤x≤m+1},当B A时,求实数m的取值范围.
-3
4
2m-1 m+1
解:由题意,知
-3 ≤ 2m-1, m+1 ≤ 4
∴-1≤ m ≤ 3
2m-1≤m+1
课堂练习
以下六个关系式:① { }
∈{ } ③ {0} φ ④0 φ⑤ φ≠{0} ⑥φ={φ},其中正确的序号是:
①②③④⑤
小结
1.子集,真子集的概念与性质;
3.集合与集合,元素与集合的
关系.
2. 集合的相等;
再见!
谢谢大家!
点滴积累 丰富人生
观察以下几组集合,并指出它们元
素间的关系:
① A={1,2,3}, B={1,2,3,4,5};
② A={x|x>1}, B={x|x2>1};
③ A={四边形}, B={多边形};
④ A={x|x-3=0}, B={x|x > 2} .
集合A的元素都在B中!
子集定义:
Venn图:
B
A B
A
图1-1
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
×
×
√
√
集合相等定义:
若A B且B A,
则A=B;
反之,亦然.
观察集合A与集合B的关系:
(1)A={1,3,5}, B={1,2,3,4,5,6}
(2) A={四边形}, B={多边形}
A B
A B
(1) A={a,b,c,d}, B={d,b,c,a}
(2) A={-1,1}, B={x x2-1=0}
观察集合A与集合B的关系:
A = B
A =B
B
A
图中A是否为B的子集
(1)
B
A
(2)
A不是B的子集
⑴ 集合A不包含于集合B,或集合B不包含集合A时,
记作 A B 或B A
注 意
⑵ 空集:我们把不含任何元素的集合叫做空集,记作:
A
规定:空集是任何集合的子集.
即对任何集合A,都有:
真子集定义:
图示为
A
B
观察集合A与集合B的关系:
(1)A={1,3,5}, B={1,2,3,4,5,6}
(2) A={四边形}, B={多边形}
子集的性质
(1)对任何集合A,都有:
A A
(2)对于集合A,B,C,若A B,且B
C,则有 A C
(3)空集是任何非空集合的真子集.
例题讲解
例1 写出{0,1,2}的所有子集,并指出其中哪些是它的真子集.
解:{0,1,2}的所有子集为:
{0}
{1}
{2}
{0,1}
{0, 2}
{1,2}
{0,1,2}
{0,1,2}的所有真子集为:
{0}
{1}
{2}
{0,1}
{0, 2}
{1,2}
例题讲解
例2 设A={x,x2,xy}, B={1,x,y},且A=B,求实数x,y的值.
解:∵{x,x2,xy}={1,x,y},
∴x2=1且xy=y,
或x2= y或 xy=1,
∴x=-1,y=0
例题讲解
例3 若A={x |-3≤x≤4}, B={x|2m-1≤x≤m+1},当B A时,求实数m的取值范围.
-3
4
2m-1 m+1
解:由题意,知
-3 ≤ 2m-1, m+1 ≤ 4
∴-1≤ m ≤ 3
2m-1≤m+1
课堂练习
以下六个关系式:① { }
∈{ } ③ {0} φ ④0 φ⑤ φ≠{0} ⑥φ={φ},其中正确的序号是:
①②③④⑤
小结
1.子集,真子集的概念与性质;
3.集合与集合,元素与集合的
关系.
2. 集合的相等;
再见!
谢谢大家!
点滴积累 丰富人生
